北师大版八年级数学下册 6.2平行四边形的判定 第1课时 利用四边形边的关系判定平行四边形课件 (共29张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 6.2平行四边形的判定 第1课时 利用四边形边的关系判定平行四边形课件 (共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 665.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 20:07:20 | ||
图片预览



文档简介
6.2
平行四边形的判定
第六章
平行四边形
第1课时
利用四边形边的关系判定平行四边形
情境引入
学习目标
1.掌握平行四边形的判定定理;(重点)
2.综合运用平行四边形的性质与判定定理1、2解决问题.(难点)
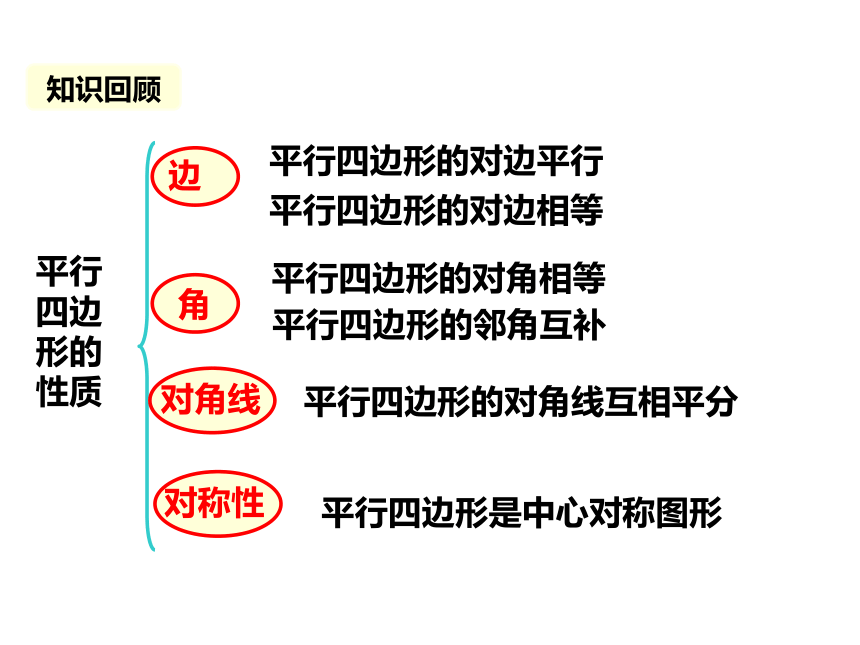
平行四边形的性质
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
对称性
平行四边形是中心对称图形
对角线
知识回顾
我们已经知道,如果一个四边形是平行四边形,那么它就是
一个中心对称图形,具有如下的一些性质:
1.两组对边分别平行且相等;
2.两组对角分别相等;
3.两条对角线互相平分.
那么,怎样判定一个四边形是否是平行四边形呢?
当然,我们可以根据平行四边形的原始定义:
两组对边分别平行的四边形是平行四边形加以判定.
那么是否存在其他的判定方法呢?
情境导入
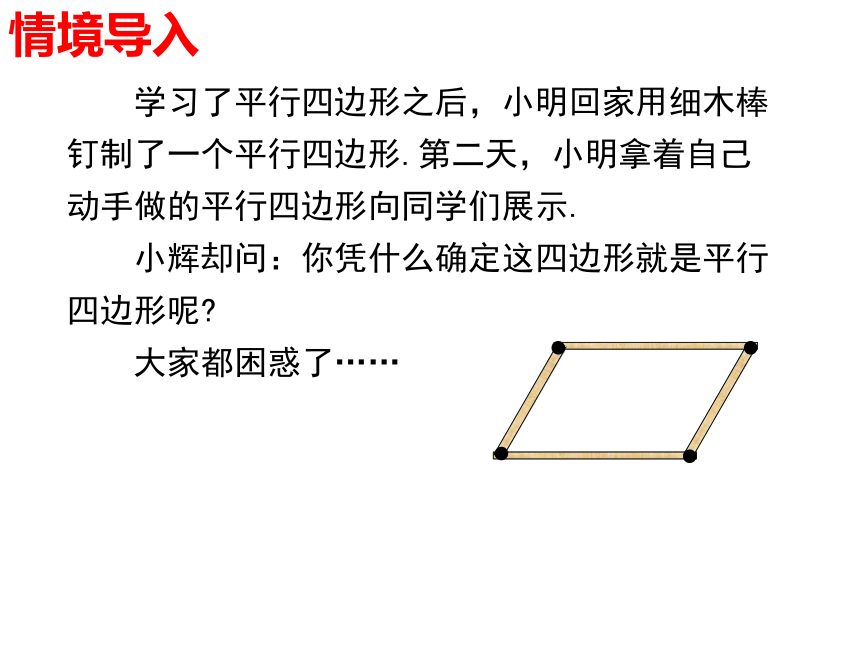
学行四边形之后,小明回家用细木棒钉制了一个平行四边形.第二天,小明拿着自己动手做的平行四边形向同学们展示.
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……
情境导入
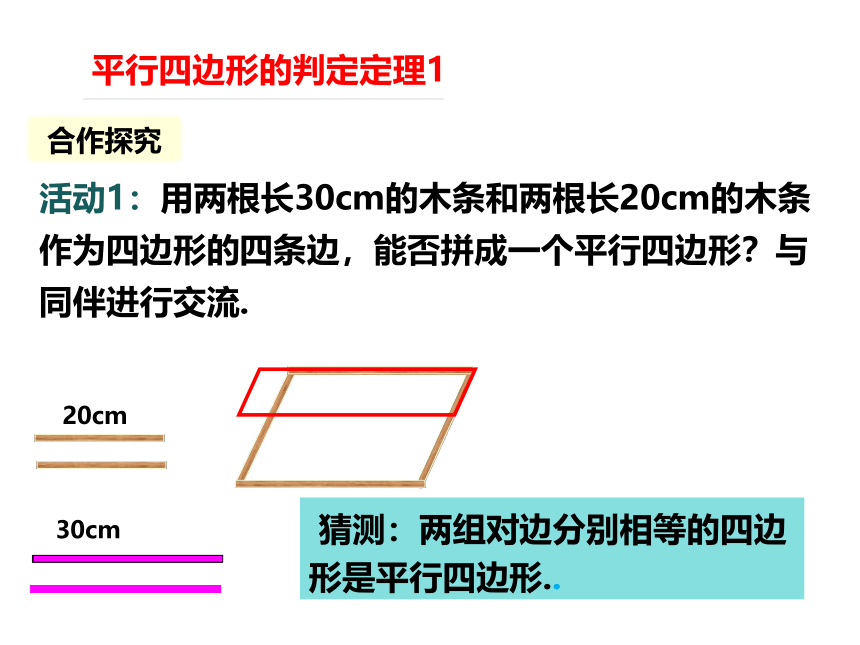
活动1:用两根长30cm的木条和两根长20cm的木条作为四边形的四条边,能否拼成一个平行四边形?与同伴进行交流.
20cm
30cm
猜测:两组对边分别相等的四边形是平行四边形..
平行四边形的判定定理1
合作探究
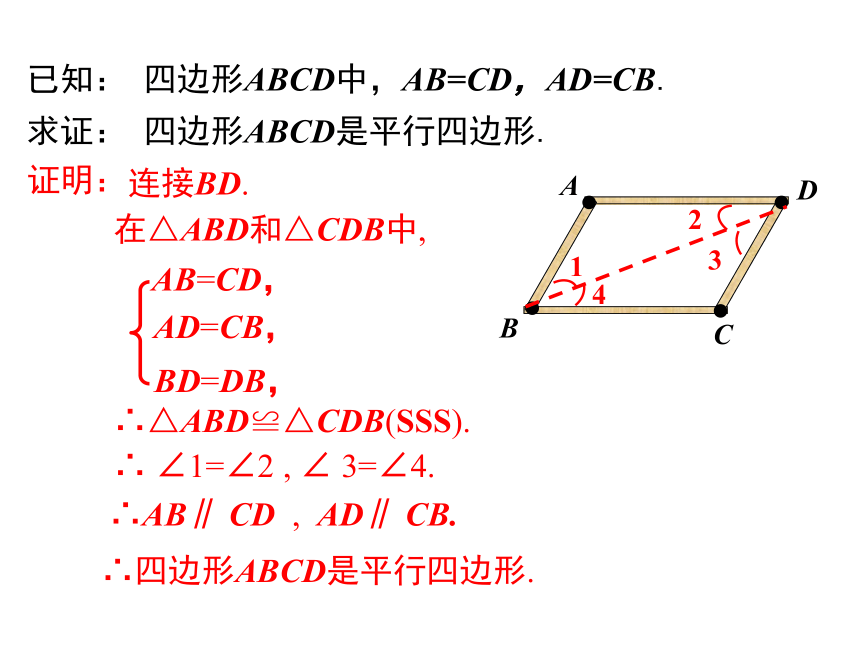
已知:
四边形ABCD中,AB=CD,AD=CB.
求证:
四边形ABCD是平行四边形.
A
B
C
D
连接BD.
在△ABD和△CDB中,
AB=CD,
BD=DB,
AD=CB,
∴△ABD≌△CDB(SSS).
∴
∠1=∠2
,
∠
3=∠4.
∴AB∥
CD
,
AD∥
CB.
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
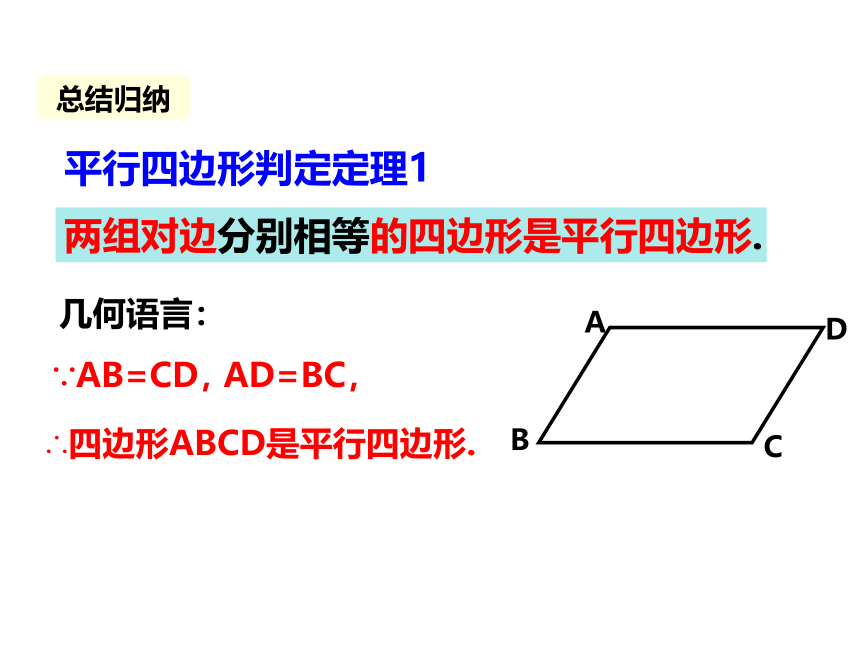
两组对边分别相等的四边形是平行四边形.
∵AB=CD,
AD=BC,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
A
总结归纳
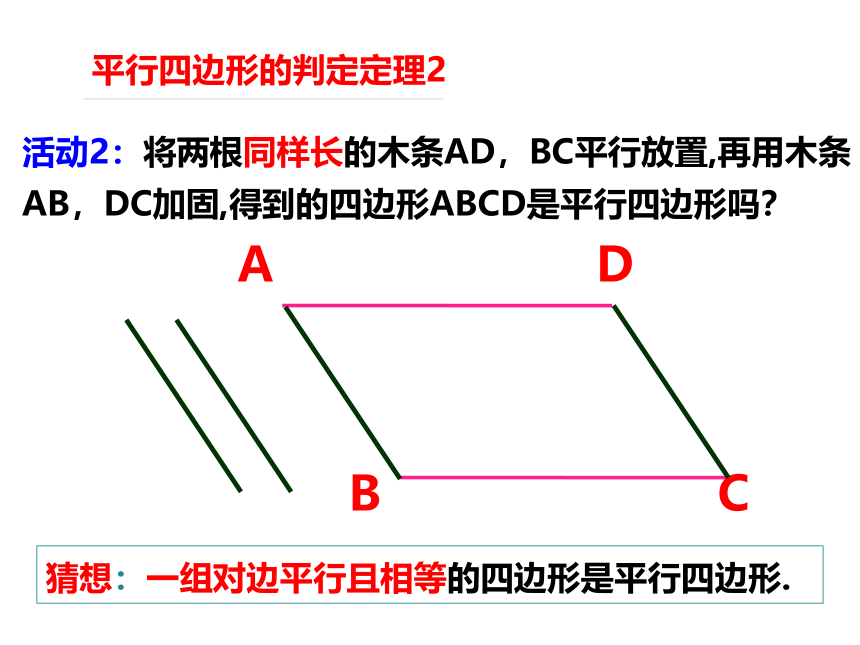
活动2:将两根同样长的木条AD,BC平行放置,再用木条AB,DC加固,得到的四边形ABCD是平行四边形吗?
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形.
平行四边形的判定定理2
连接AC.
∵AB//CD,
∴∠1=∠2.
又AB=CD,AC=CA,
∴△ABC≌△CDA(SAS).
∴BC=DA.
∴四边形ABCD的两组对边分别相等,它是平行四边形.
D
A
B
C
已知:如图,在四边形ABCD中,AB=CD,AB//CD.
求证:四边形ABCD是平行四边形.
证明:
1
2
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,
AB∥CD,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理2
B
D
C
A
总结归纳
例2
如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的平分线,试证明四边形AFCE是平行四边形.
证明:∵在平行四边形ABCD中,
AE、CF分别是∠DAB、
∠BCD的平分线,
∴∠B=∠D,AB=CD,
AD∥BC,
∠BAE=∠DCF=
∠DAB=
∠BCD.
∴△ABE≌△CDF(ASA).
∴BE=DF.∴AF=CE.
∵AF∥CE,∴四边形AFCE是平行四边形(一组对边平行且相等的四边形是平行四边形).
卢师傅要做一个平行四边形木框.他要从图中几根木条中选出四根来制作,可是他不知道该怎样选,请同学们帮他选一选,哪四根木条可以制作成平行四边形木框,为什么?
7cm
4cm
3cm
3cm
5cm
4cm
阅读思考
4cm
4cm
4cm
4cm
3cm
3cm
3cm
发现:一组对边平行,另一组对边相等的四边形不一定是平行四边形;四条边两两相等的四边形不一定是平行四边形.
5cm
3cm
4cm
3cm
4cm
思考:我们可以从角出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
由定义判定平行四边形
已知:四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
A
B
C
D
又∵∠A=∠C,∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
∴2∠A+2∠B=360°,
即∠A+∠B=180°.
∴
AD∥BC.
∴四边形ABCD是平行四边形.
同理得
AB∥
CD.
证明:
定义判定:
两组对角分别相等的四边形是平行四边形
归纳小结
判定
定理1
定理2
定义拓展
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,
∴四边形ABCD是
ABCD
A
B
C
D
∵
AB=
CD,
AB∥CD,
∴四边形ABCD是
ABCD
∵
∠
A=
∠
C,
∠
B=
∠
D,
∴四边形ABCD是
ABCD
A
B
C
D
1.下列∠A:∠B:∠C:∠D的值中,能判定四边形ABCD是平行四边形的是( )
A.
1:2:3:4
B.
1:4:2:3
C.
1:2:2:1
D.
3:2:3:2
D
当堂跟踪练习
2.已知AD//BC
,要使这个四边形ABCD为平行四边形,需要增加条件
.
AD=BC(答案不唯一)
3.已知:如图,E,F分别是
平行四边形ABCD
的边AD,BC的中点.
求证:四边形EBFD是平行四边形.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC
,
AD=BC.
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED
BF.
∥
﹦
∴四边形EBFD是平行四边形(一组对边平行并且相等的四边形是平行四边形).
A
B
C
D
E
F
解:是,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD.
∴∠ABE=∠CDF.
∴∠AEB=∠CFD=90°.
∴△ABE≌△CDF(AAS).
∴AE=CF.
∵
∠AEF=∠CFE=900,
∴AE//CF.
∴四边形AECF是平行四边形.
4
1.现有一块等腰直角三角形铁板,要求切割一次,焊接成一个含有45°角的平行四边形
(不能有余料),
请你设计一种方案,并说明该方案正确的理由.
A
B
C
能力提升
C
A
B
F
E
D
D
C
A
B
E
A
B
C
F
D
E
2.电视剧《人民的名义》中有一位退休好干部叫陈岩石,他有一块平行四边形菜园地,夏季到来了,院子里瓜果飘香.有一天突然下起了暴雨,将菜园地的一部分冲垮,陈老的菜园地与邻居家的菜园地之间的界限看不清了,巧的是,刚好保留了顶点A和C.
(1)如图,若你只有一把直尺和一个圆规,你能将图形补全吗?若能,请补全图形(不写作法,只保留作图痕迹),并证明四边形ABCD是平行四边形;
A
B
C
(2)若E是BC边上的一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
①作出满足题意的点F,简要说明作图过程;
②依据你的作图,证明:DF=BE.
A
B
C
★
E
A
B
C
D
O
F
课堂小结
平行四边形的判定
定义及拓展
判定定理1
判定定理2
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形
1.平行四边形的判定定理(1)
两组对边分别相等的四边形是平行四边形.
2.平行四边形的判定定理(2)
一组对边平行且相等的四边形是平行四边形.
板书设计
在整个教学过程中,以学生看、想、议、练为主体,教师在学生仔细观察、类比、想象的基础上加以引导点拨.判定方法是学生自己探讨发现的,因此,应用也就成了学生自发的需要,用起来更加得心应手.在证明命题的过程中,学生自然将判定方法进行对比和筛选,或对一题进行多解,便于思维发散,不把思路局限在某一判定方法上.
教学反思
平行四边形的判定
第六章
平行四边形
第1课时
利用四边形边的关系判定平行四边形
情境引入
学习目标
1.掌握平行四边形的判定定理;(重点)
2.综合运用平行四边形的性质与判定定理1、2解决问题.(难点)
平行四边形的性质
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
对称性
平行四边形是中心对称图形
对角线
知识回顾
我们已经知道,如果一个四边形是平行四边形,那么它就是
一个中心对称图形,具有如下的一些性质:
1.两组对边分别平行且相等;
2.两组对角分别相等;
3.两条对角线互相平分.
那么,怎样判定一个四边形是否是平行四边形呢?
当然,我们可以根据平行四边形的原始定义:
两组对边分别平行的四边形是平行四边形加以判定.
那么是否存在其他的判定方法呢?
情境导入
学行四边形之后,小明回家用细木棒钉制了一个平行四边形.第二天,小明拿着自己动手做的平行四边形向同学们展示.
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……
情境导入
活动1:用两根长30cm的木条和两根长20cm的木条作为四边形的四条边,能否拼成一个平行四边形?与同伴进行交流.
20cm
30cm
猜测:两组对边分别相等的四边形是平行四边形..
平行四边形的判定定理1
合作探究
已知:
四边形ABCD中,AB=CD,AD=CB.
求证:
四边形ABCD是平行四边形.
A
B
C
D
连接BD.
在△ABD和△CDB中,
AB=CD,
BD=DB,
AD=CB,
∴△ABD≌△CDB(SSS).
∴
∠1=∠2
,
∠
3=∠4.
∴AB∥
CD
,
AD∥
CB.
∴四边形ABCD是平行四边形.
证明:
1
4
2
3
两组对边分别相等的四边形是平行四边形.
∵AB=CD,
AD=BC,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
A
总结归纳
活动2:将两根同样长的木条AD,BC平行放置,再用木条AB,DC加固,得到的四边形ABCD是平行四边形吗?
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形.
平行四边形的判定定理2
连接AC.
∵AB//CD,
∴∠1=∠2.
又AB=CD,AC=CA,
∴△ABC≌△CDA(SAS).
∴BC=DA.
∴四边形ABCD的两组对边分别相等,它是平行四边形.
D
A
B
C
已知:如图,在四边形ABCD中,AB=CD,AB//CD.
求证:四边形ABCD是平行四边形.
证明:
1
2
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,
AB∥CD,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理2
B
D
C
A
总结归纳
例2
如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的平分线,试证明四边形AFCE是平行四边形.
证明:∵在平行四边形ABCD中,
AE、CF分别是∠DAB、
∠BCD的平分线,
∴∠B=∠D,AB=CD,
AD∥BC,
∠BAE=∠DCF=
∠DAB=
∠BCD.
∴△ABE≌△CDF(ASA).
∴BE=DF.∴AF=CE.
∵AF∥CE,∴四边形AFCE是平行四边形(一组对边平行且相等的四边形是平行四边形).
卢师傅要做一个平行四边形木框.他要从图中几根木条中选出四根来制作,可是他不知道该怎样选,请同学们帮他选一选,哪四根木条可以制作成平行四边形木框,为什么?
7cm
4cm
3cm
3cm
5cm
4cm
阅读思考
4cm
4cm
4cm
4cm
3cm
3cm
3cm
发现:一组对边平行,另一组对边相等的四边形不一定是平行四边形;四条边两两相等的四边形不一定是平行四边形.
5cm
3cm
4cm
3cm
4cm
思考:我们可以从角出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
由定义判定平行四边形
已知:四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
A
B
C
D
又∵∠A=∠C,∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
∴2∠A+2∠B=360°,
即∠A+∠B=180°.
∴
AD∥BC.
∴四边形ABCD是平行四边形.
同理得
AB∥
CD.
证明:
定义判定:
两组对角分别相等的四边形是平行四边形
归纳小结
判定
定理1
定理2
定义拓展
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,
∴四边形ABCD是
ABCD
A
B
C
D
∵
AB=
CD,
AB∥CD,
∴四边形ABCD是
ABCD
∵
∠
A=
∠
C,
∠
B=
∠
D,
∴四边形ABCD是
ABCD
A
B
C
D
1.下列∠A:∠B:∠C:∠D的值中,能判定四边形ABCD是平行四边形的是( )
A.
1:2:3:4
B.
1:4:2:3
C.
1:2:2:1
D.
3:2:3:2
D
当堂跟踪练习
2.已知AD//BC
,要使这个四边形ABCD为平行四边形,需要增加条件
.
AD=BC(答案不唯一)
3.已知:如图,E,F分别是
平行四边形ABCD
的边AD,BC的中点.
求证:四边形EBFD是平行四边形.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC
,
AD=BC.
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED
BF.
∥
﹦
∴四边形EBFD是平行四边形(一组对边平行并且相等的四边形是平行四边形).
A
B
C
D
E
F
解:是,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD.
∴∠ABE=∠CDF.
∴∠AEB=∠CFD=90°.
∴△ABE≌△CDF(AAS).
∴AE=CF.
∵
∠AEF=∠CFE=900,
∴AE//CF.
∴四边形AECF是平行四边形.
4
1.现有一块等腰直角三角形铁板,要求切割一次,焊接成一个含有45°角的平行四边形
(不能有余料),
请你设计一种方案,并说明该方案正确的理由.
A
B
C
能力提升
C
A
B
F
E
D
D
C
A
B
E
A
B
C
F
D
E
2.电视剧《人民的名义》中有一位退休好干部叫陈岩石,他有一块平行四边形菜园地,夏季到来了,院子里瓜果飘香.有一天突然下起了暴雨,将菜园地的一部分冲垮,陈老的菜园地与邻居家的菜园地之间的界限看不清了,巧的是,刚好保留了顶点A和C.
(1)如图,若你只有一把直尺和一个圆规,你能将图形补全吗?若能,请补全图形(不写作法,只保留作图痕迹),并证明四边形ABCD是平行四边形;
A
B
C
(2)若E是BC边上的一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
①作出满足题意的点F,简要说明作图过程;
②依据你的作图,证明:DF=BE.
A
B
C
★
E
A
B
C
D
O
F
课堂小结
平行四边形的判定
定义及拓展
判定定理1
判定定理2
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形
1.平行四边形的判定定理(1)
两组对边分别相等的四边形是平行四边形.
2.平行四边形的判定定理(2)
一组对边平行且相等的四边形是平行四边形.
板书设计
在整个教学过程中,以学生看、想、议、练为主体,教师在学生仔细观察、类比、想象的基础上加以引导点拨.判定方法是学生自己探讨发现的,因此,应用也就成了学生自发的需要,用起来更加得心应手.在证明命题的过程中,学生自然将判定方法进行对比和筛选,或对一题进行多解,便于思维发散,不把思路局限在某一判定方法上.
教学反思
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
