北师大版八年级数学下册第三章图形的平移与旋转复习课件(19张PPT)
文档属性
| 名称 | 北师大版八年级数学下册第三章图形的平移与旋转复习课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 646.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 20:11:40 | ||
图片预览




文档简介
(共19张PPT)
第三章综合复习及检测
八年级数学下册
第三章 图形的平移与旋转 复习及检测
知识框架一
平移
平移
的概念
平移
的性质
一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等。
坐标系中的平移
一个图形依次沿x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的。
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
旋转
旋转的概念
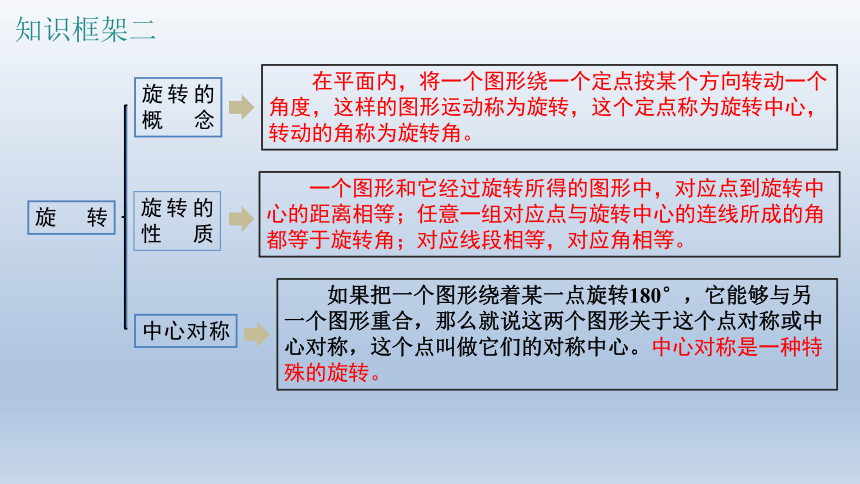
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。
旋转的性质
一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等;任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等。
中心对称
如果把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心。中心对称是一种特殊的旋转。
知识框架二
题号 1题 5金币 2题 5金币 3题 15金币 4题 10金币 5题 10金币 6题 5金币 7题 5金币 合计
55金币
收获
第三章 图形的平移与旋转
复习与检测
考点一 平移
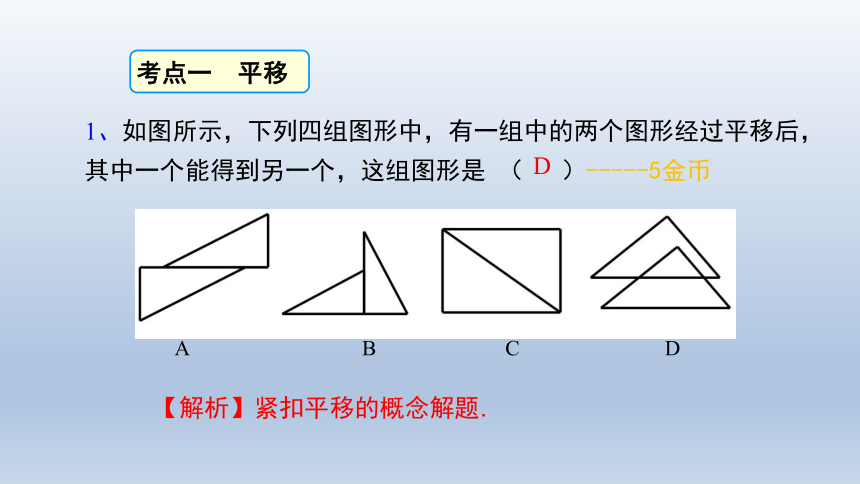
1、如图所示,下列四组图形中,有一组中的两个图形经过平移后,其中一个能得到另一个,这组图形是 ( )-----5金币
D
A B C D
【解析】紧扣平移的概念解题.
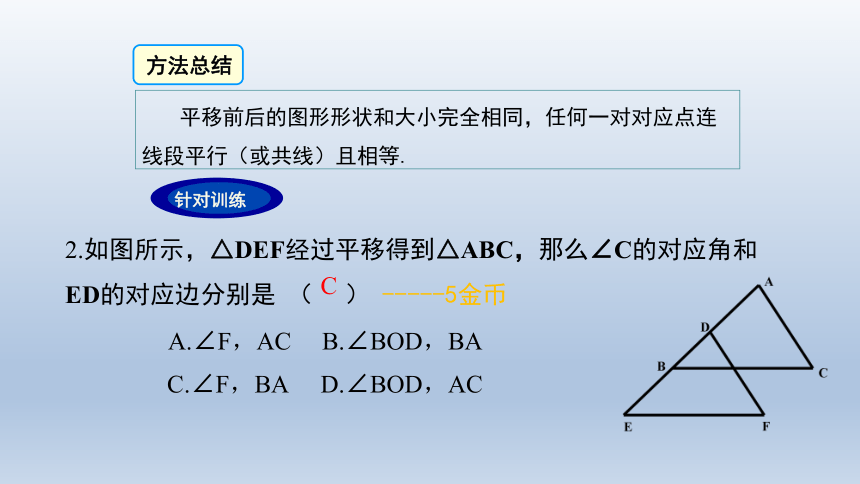
平移前后的图形形状和大小完全相同,任何一对对应点连线段平行(或共线)且相等.
方法总结
针对训练
2.如图所示,△DEF经过平移得到△ABC,那么∠C的对应角和ED的对应边分别是 ( ) -----5金币
A.∠F,AC
B.∠BOD,BA
C.∠F,BA
D.∠BOD,AC
C
考点二 坐标系中的图形平移
3、如图,直角坐标系中,△ABC的顶点都在网格点上,其
中,C点坐标为(1,2). -----15金币
(1)写出点A、B的坐标:A( , )、B( , );
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位
长度,得到△A′B′C′,则△A′B′C′的三个顶点
坐标分别是 A′( , )、 B′( , )、
C′( , );
(3)求△ABC的面积.
2
-1
4
3
0
0
2
4
-1
3
【分析】(1)根据图形写出相应点的坐标即可;(2)画出平移后图形,根据图形解题即可,或是让三个点的横坐标减去2,纵坐标加1即可得到平移后相应点的坐标;(3)△ABC的面积等于长为4,宽为3的长方形的面积减去2个直角边长为1,3和一个直角边长为2,4的3个直角三角形的面积.
解:(3)△ABC的面积
S=3×4﹣2× ×1×3﹣ ×2×4
=5.
A′
B′
C′
方法总结
直角坐标系中的图形左右移动改变点的横坐标,即左减右加;上下平移改变点的纵坐标,即上加下减.求格点中图形的面积通常用割补法,常用长方形的面积减去若干直角三角形的面积表示,或是转化为用几个比较容易求的三角形或四边形的面积和来表示.
针对训练
4.如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2), -----10金币
(1)请画出上述平移后的△A1B1C1,并写出点A、C、A1、C1的坐标;
(2)求出以A、C、A1、C1为顶
点的四边形的面积.
解:(1)△A1B1C1如图所示;各点的坐标为:
A (﹣3,2)、C(﹣2,0)
A1(3,4)、C1(4,2);
(2)如图,连接AA1、CC1;
△AC1C的面积 :
△AC1A1的面积:
四边形ACC1A1的面积为7+7=14.
4.如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2),
(1)请画出上述平移后的△A1B1C1,并写出点A、C、A1、C1的坐标;
(2)求出以A、C、A1、C1为顶点的四边形的面积.
考点三 旋转的概念及性质的应用
5、(1)如图a,将△AOB绕点O按逆时针方
向旋转60 °后得到△COD,若∠AOB=15 °,
则∠AOD的度数是( ) -----5金币
A. 15 ° B. 60 ° C. 45 ° D. 75 °
(2) 如图b ,在4 ×4的正方形网格中, △MNP绕某
点旋转一定的角度,得到△M1N1P1,其旋转中
心是( ) -----5金币
A. 点A B. 点B C. 点C D. 点D
A
B
O
D
C
图a
C
N1
M1
N
M
P1
D
P
A
B
图b
C
B
【解析】(1)关键找出旋转角∠BOD=60 °;
(2)作线段MM1与PP1 的垂直平分线,交点便是旋转中心.
针对训练
6.如图,在等腰Rt△ABC中,点O是AB的中点,AC=4, 将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为D,另一条直角边与BC相交,交点为E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和等于 . -----5金币
A
B
C
D
E
O
4
考点四 中心对称
7、下列图形中,既是轴对称图形,又是中心对称图形的是( ). -----5金币
A B C D
D
【解析】 图A.图B都是轴对称图形,图C是中心对称图形,图D既是中心对称图形也是轴对称图形.
第三章
你收获 ?
作业:
1、纠正做错的题目
2、复习巩固学过的知识点。
谢谢大家的聆听
再 见
第三章综合复习及检测
八年级数学下册
第三章 图形的平移与旋转 复习及检测
知识框架一
平移
平移
的概念
平移
的性质
一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等。
坐标系中的平移
一个图形依次沿x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的。
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
旋转
旋转的概念
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。
旋转的性质
一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等;任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等。
中心对称
如果把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心。中心对称是一种特殊的旋转。
知识框架二
题号 1题 5金币 2题 5金币 3题 15金币 4题 10金币 5题 10金币 6题 5金币 7题 5金币 合计
55金币
收获
第三章 图形的平移与旋转
复习与检测
考点一 平移
1、如图所示,下列四组图形中,有一组中的两个图形经过平移后,其中一个能得到另一个,这组图形是 ( )-----5金币
D
A B C D
【解析】紧扣平移的概念解题.
平移前后的图形形状和大小完全相同,任何一对对应点连线段平行(或共线)且相等.
方法总结
针对训练
2.如图所示,△DEF经过平移得到△ABC,那么∠C的对应角和ED的对应边分别是 ( ) -----5金币
A.∠F,AC
B.∠BOD,BA
C.∠F,BA
D.∠BOD,AC
C
考点二 坐标系中的图形平移
3、如图,直角坐标系中,△ABC的顶点都在网格点上,其
中,C点坐标为(1,2). -----15金币
(1)写出点A、B的坐标:A( , )、B( , );
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位
长度,得到△A′B′C′,则△A′B′C′的三个顶点
坐标分别是 A′( , )、 B′( , )、
C′( , );
(3)求△ABC的面积.
2
-1
4
3
0
0
2
4
-1
3
【分析】(1)根据图形写出相应点的坐标即可;(2)画出平移后图形,根据图形解题即可,或是让三个点的横坐标减去2,纵坐标加1即可得到平移后相应点的坐标;(3)△ABC的面积等于长为4,宽为3的长方形的面积减去2个直角边长为1,3和一个直角边长为2,4的3个直角三角形的面积.
解:(3)△ABC的面积
S=3×4﹣2× ×1×3﹣ ×2×4
=5.
A′
B′
C′
方法总结
直角坐标系中的图形左右移动改变点的横坐标,即左减右加;上下平移改变点的纵坐标,即上加下减.求格点中图形的面积通常用割补法,常用长方形的面积减去若干直角三角形的面积表示,或是转化为用几个比较容易求的三角形或四边形的面积和来表示.
针对训练
4.如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2), -----10金币
(1)请画出上述平移后的△A1B1C1,并写出点A、C、A1、C1的坐标;
(2)求出以A、C、A1、C1为顶
点的四边形的面积.
解:(1)△A1B1C1如图所示;各点的坐标为:
A (﹣3,2)、C(﹣2,0)
A1(3,4)、C1(4,2);
(2)如图,连接AA1、CC1;
△AC1C的面积 :
△AC1A1的面积:
四边形ACC1A1的面积为7+7=14.
4.如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2),
(1)请画出上述平移后的△A1B1C1,并写出点A、C、A1、C1的坐标;
(2)求出以A、C、A1、C1为顶点的四边形的面积.
考点三 旋转的概念及性质的应用
5、(1)如图a,将△AOB绕点O按逆时针方
向旋转60 °后得到△COD,若∠AOB=15 °,
则∠AOD的度数是( ) -----5金币
A. 15 ° B. 60 ° C. 45 ° D. 75 °
(2) 如图b ,在4 ×4的正方形网格中, △MNP绕某
点旋转一定的角度,得到△M1N1P1,其旋转中
心是( ) -----5金币
A. 点A B. 点B C. 点C D. 点D
A
B
O
D
C
图a
C
N1
M1
N
M
P1
D
P
A
B
图b
C
B
【解析】(1)关键找出旋转角∠BOD=60 °;
(2)作线段MM1与PP1 的垂直平分线,交点便是旋转中心.
针对训练
6.如图,在等腰Rt△ABC中,点O是AB的中点,AC=4, 将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为D,另一条直角边与BC相交,交点为E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和等于 . -----5金币
A
B
C
D
E
O
4
考点四 中心对称
7、下列图形中,既是轴对称图形,又是中心对称图形的是( ). -----5金币
A B C D
D
【解析】 图A.图B都是轴对称图形,图C是中心对称图形,图D既是中心对称图形也是轴对称图形.
第三章
你收获 ?
作业:
1、纠正做错的题目
2、复习巩固学过的知识点。
谢谢大家的聆听
再 见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
