北师大版八年级下册数学课件1.1.3等腰三角形(三)(共17张PPT)
文档属性
| 名称 | 北师大版八年级下册数学课件1.1.3等腰三角形(三)(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 348.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 20:31:56 | ||
图片预览




文档简介
等腰三角形的两个底角相等(等边对等角),反过来,有两个角相等的三角形是等腰三角形吗?(也就是等角对等边吗?)
议一议
已知:如图,在△ABC中,∠B=∠C,
求证:AB=AC.
C
B
A
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
条件
条件
条件
条件
结论
有两个角相等的三角形是等腰三角形 (等角对等边)
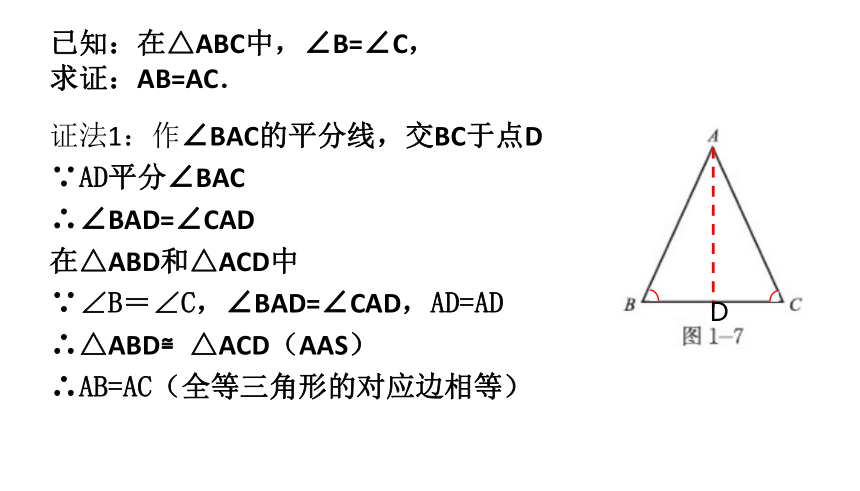
已知:在△ABC中,∠B=∠C,
求证:AB=AC.
证法1:作∠BAC的平分线,交BC于点D
∵AD平分∠BAC
∴∠BAD=∠CAD
在△ABD和△ACD中
∵∠B=∠C,∠BAD=∠CAD,AD=AD
∴△ABD≌△ACD(AAS)
∴AB=AC(全等三角形的对应边相等)
D
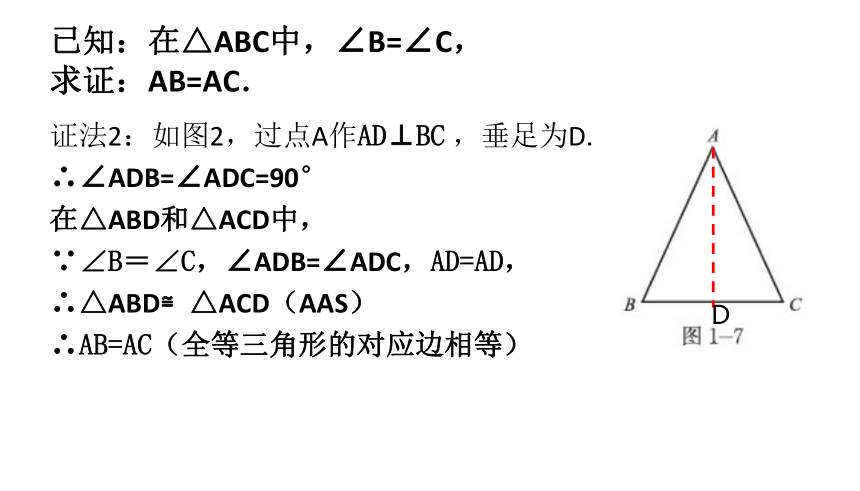
已知:在△ABC中,∠B=∠C,
求证:AB=AC.
证法2:如图2,过点A作AD⊥BC ,垂足为D.
∴∠ADB=∠ADC=90°
在△ABD和△ACD中,
∵∠B=∠C,∠ADB=∠ADC,AD=AD,
∴△ABD≌△ACD(AAS)
∴AB=AC(全等三角形的对应边相等)
D
定理:有两个角相等的三角形是等腰三角形.
(等角对等边.)
等腰三角形的判定定理:
在△ABC中
∵∠B=∠C(已知),
∴AB=AC(等角对等边).
A
C
B
几何语言:
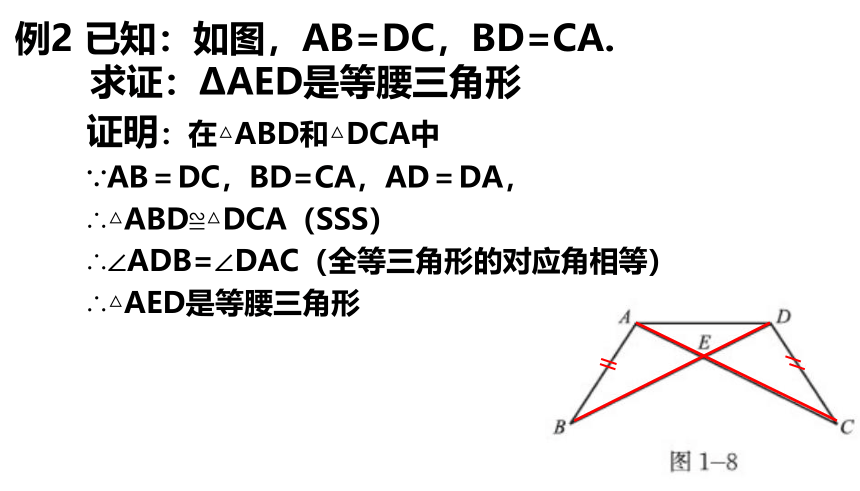
例2 已知:如图,AB=DC,BD=CA.
求证:?AED是等腰三角形
证明:在△ABD和△DCA中
∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS)
∴∠ADB=∠DAC(全等三角形的对应角相等)
∴△AED是等腰三角形
想一想
小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗?如果成立,你能证明它吗?
证明:
假设AB=AC,那么根据“等边对等角”定理可得∠C=∠B,这与已知条件“∠B≠∠C”相矛盾,因此 AB≠AC
图1-9
已知:如图,在△ABC中,∠B≠∠C,
求证:AB≠AC.
在上面的证法中,先假设命题的结论不成立,然后由此推导出了与已知或定义或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.我们把它叫做反证法.
例3用反证法证明△ABC中不可能有两个直角
已知: △ABC
求证:∠A,∠B,∠C中不能有两个角是直角。
证明:假设 ∠A,∠B,∠C中有两个角是直角,不妨设∠A=90°,∠B=90°,可得在△ABC中∠A+∠B+∠C=90°+90°+∠C>180°
这与三角形内角和定理相矛盾,因此“∠A=90°,∠B=90°”的假设不成立。
因此△ABC中不可能有两个直角.
随堂练习1.如图,在?ABC中,BD平分∠ABC,交AC于点D,过点D作DE∥BC,交AB于点E,请判断?BDE的形状,并说明理由。
解:?BDE是等腰三角形。理由如下:
∵BD平分∠ABC
∴∠EBD=∠DBC
∵DE∥BC
∴∠EDB=∠DBC
∴∠EBD=∠EDB
∴?BDE是等腰三角形
随堂练习2.已知:a1,a2,a3,a4,a5都是正数,且a1+a2+a3+a4+a5=1,求证:这五个数中至少有一个大于或等于1/5.
用反证法来证:
证明:假设这五个数全部小于1/5,那么这五个数的和a1+a2+a3+a4+a5就小于1.这与已知这五个数的和a1+a2+a3+a4+a5=1相矛盾.
因此假设不成立, 原命题成立,即这五个数中至少有一个大于或等于1/5.
1已知:如图,∠CAE是△ABC的外角,AD∥BC且∠1=∠2.
求证:AB=AC.
习题1.3
证明∵AD∥BC
∴∠1=∠B,∠2=∠C
又∵∠1=∠2
∴∠B=∠C
∴AB=AC(等角对等边)
2.已知:如图,在△ABC中,AB=AC,点E在CA的延长线上,EP┴BC,垂足为P,EP交AB于点F,求证:△AEF是等腰三角形。
证法一:∵在△ABC中,AB=AC
∴∠B=∠C
∵EP┴BC,∴∠FPB=∠FPC=90°
在△BFP中,∠BFP=180°-∠B-∠FPB,
在△EPC中,∠PEC=180°-∠C-∠ECP,
∴∠BFP=∠PEC
∵∠BFP=∠AFE
∴∠PEC=∠AFE
∴△AEF是等腰三角形。
2.已知:如图,在△ABC中,AB=AC,点E在CA的延长线上,EP┴BC,垂足为P,EP交AB于点F,求证:△AEF是等腰三角形。
证法二:作△ABC底边BC上的高线AD,∵EP┴BC,
∴AD∥EP
∴∠E=∠CAD,∠EFA=∠BAD,
又∵△ABC中,AB=AC,
∴∠BAD=∠CAD(三线合一)
∴∠EFA=∠E
∴△AEF是等腰三角形
D
3.(1)已知:如图(甲),等腰三角形的一个内角为锐角ɑ,求作这个等腰三角形;
(2)在(1)中,把锐角ɑ变成钝角ɑ,其他条件不变,求作这个等腰三角形
提示:有两个结果。
提示:有一种结果。
4.如图,一艘船从A处出发,以18kn的速度向正北航行,经过10h到达B处,分别从A,B望灯塔C,测得∠NAC=42°,∠NBC=84°,求从B处到灯塔C的距离。
解:∵∠NBC是△ABC的一个外角,∠NAC=42°,∠NBC=84°
∴∠C=∠NBC-∠NAC=42°
∴AB=BC
∵AB=18kn×10h=180 nmile
∴BC=180 n mile
(1)等腰三角形的判定方法有哪几种?
(2)举例谈谈用反证法说理的基本思路
课堂小结
议一议
已知:如图,在△ABC中,∠B=∠C,
求证:AB=AC.
C
B
A
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
条件
条件
条件
条件
结论
有两个角相等的三角形是等腰三角形 (等角对等边)
已知:在△ABC中,∠B=∠C,
求证:AB=AC.
证法1:作∠BAC的平分线,交BC于点D
∵AD平分∠BAC
∴∠BAD=∠CAD
在△ABD和△ACD中
∵∠B=∠C,∠BAD=∠CAD,AD=AD
∴△ABD≌△ACD(AAS)
∴AB=AC(全等三角形的对应边相等)
D
已知:在△ABC中,∠B=∠C,
求证:AB=AC.
证法2:如图2,过点A作AD⊥BC ,垂足为D.
∴∠ADB=∠ADC=90°
在△ABD和△ACD中,
∵∠B=∠C,∠ADB=∠ADC,AD=AD,
∴△ABD≌△ACD(AAS)
∴AB=AC(全等三角形的对应边相等)
D
定理:有两个角相等的三角形是等腰三角形.
(等角对等边.)
等腰三角形的判定定理:
在△ABC中
∵∠B=∠C(已知),
∴AB=AC(等角对等边).
A
C
B
几何语言:
例2 已知:如图,AB=DC,BD=CA.
求证:?AED是等腰三角形
证明:在△ABD和△DCA中
∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS)
∴∠ADB=∠DAC(全等三角形的对应角相等)
∴△AED是等腰三角形
想一想
小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗?如果成立,你能证明它吗?
证明:
假设AB=AC,那么根据“等边对等角”定理可得∠C=∠B,这与已知条件“∠B≠∠C”相矛盾,因此 AB≠AC
图1-9
已知:如图,在△ABC中,∠B≠∠C,
求证:AB≠AC.
在上面的证法中,先假设命题的结论不成立,然后由此推导出了与已知或定义或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.我们把它叫做反证法.
例3用反证法证明△ABC中不可能有两个直角
已知: △ABC
求证:∠A,∠B,∠C中不能有两个角是直角。
证明:假设 ∠A,∠B,∠C中有两个角是直角,不妨设∠A=90°,∠B=90°,可得在△ABC中∠A+∠B+∠C=90°+90°+∠C>180°
这与三角形内角和定理相矛盾,因此“∠A=90°,∠B=90°”的假设不成立。
因此△ABC中不可能有两个直角.
随堂练习1.如图,在?ABC中,BD平分∠ABC,交AC于点D,过点D作DE∥BC,交AB于点E,请判断?BDE的形状,并说明理由。
解:?BDE是等腰三角形。理由如下:
∵BD平分∠ABC
∴∠EBD=∠DBC
∵DE∥BC
∴∠EDB=∠DBC
∴∠EBD=∠EDB
∴?BDE是等腰三角形
随堂练习2.已知:a1,a2,a3,a4,a5都是正数,且a1+a2+a3+a4+a5=1,求证:这五个数中至少有一个大于或等于1/5.
用反证法来证:
证明:假设这五个数全部小于1/5,那么这五个数的和a1+a2+a3+a4+a5就小于1.这与已知这五个数的和a1+a2+a3+a4+a5=1相矛盾.
因此假设不成立, 原命题成立,即这五个数中至少有一个大于或等于1/5.
1已知:如图,∠CAE是△ABC的外角,AD∥BC且∠1=∠2.
求证:AB=AC.
习题1.3
证明∵AD∥BC
∴∠1=∠B,∠2=∠C
又∵∠1=∠2
∴∠B=∠C
∴AB=AC(等角对等边)
2.已知:如图,在△ABC中,AB=AC,点E在CA的延长线上,EP┴BC,垂足为P,EP交AB于点F,求证:△AEF是等腰三角形。
证法一:∵在△ABC中,AB=AC
∴∠B=∠C
∵EP┴BC,∴∠FPB=∠FPC=90°
在△BFP中,∠BFP=180°-∠B-∠FPB,
在△EPC中,∠PEC=180°-∠C-∠ECP,
∴∠BFP=∠PEC
∵∠BFP=∠AFE
∴∠PEC=∠AFE
∴△AEF是等腰三角形。
2.已知:如图,在△ABC中,AB=AC,点E在CA的延长线上,EP┴BC,垂足为P,EP交AB于点F,求证:△AEF是等腰三角形。
证法二:作△ABC底边BC上的高线AD,∵EP┴BC,
∴AD∥EP
∴∠E=∠CAD,∠EFA=∠BAD,
又∵△ABC中,AB=AC,
∴∠BAD=∠CAD(三线合一)
∴∠EFA=∠E
∴△AEF是等腰三角形
D
3.(1)已知:如图(甲),等腰三角形的一个内角为锐角ɑ,求作这个等腰三角形;
(2)在(1)中,把锐角ɑ变成钝角ɑ,其他条件不变,求作这个等腰三角形
提示:有两个结果。
提示:有一种结果。
4.如图,一艘船从A处出发,以18kn的速度向正北航行,经过10h到达B处,分别从A,B望灯塔C,测得∠NAC=42°,∠NBC=84°,求从B处到灯塔C的距离。
解:∵∠NBC是△ABC的一个外角,∠NAC=42°,∠NBC=84°
∴∠C=∠NBC-∠NAC=42°
∴AB=BC
∵AB=18kn×10h=180 nmile
∴BC=180 n mile
(1)等腰三角形的判定方法有哪几种?
(2)举例谈谈用反证法说理的基本思路
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
