北师大版初中七年级下册数学4.2-图形的全等课件(共28张PPT)
文档属性
| 名称 | 北师大版初中七年级下册数学4.2-图形的全等课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 54.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览





文档简介
图形的全等
1.了解全等图形的概念,会判断两个图形是不是全等图形.
2.理解全等三角形的概念,能正确表示全等三角形,能识别全等三角形中的对应边、对应角.(难点)
3.掌握全等三角形的性质,能利用全等三角形的性质解决相关问题.(重点)
学习目标
知识点1 全等图形
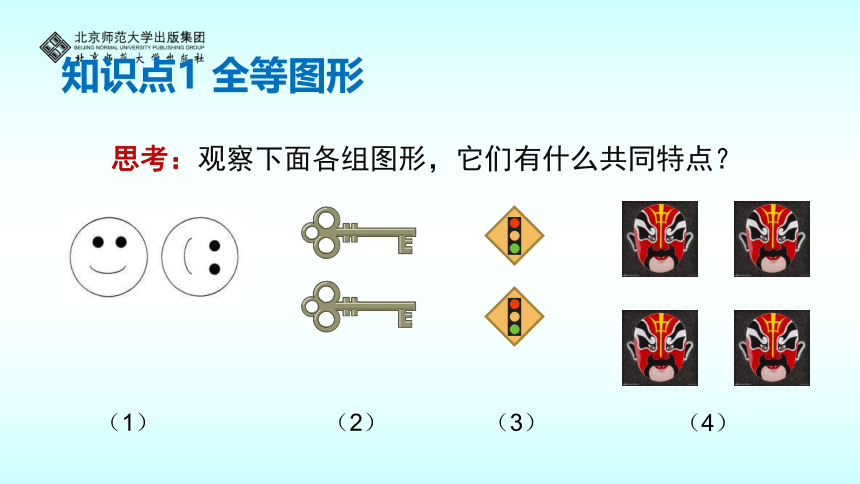
思考:观察下面各组图形,它们有什么共同特点?
(1)
(2)
(3)
(4)
知识点1 全等图形
追问 你能再举出生活中的一些类似例子吗?
(5)
(6)
(7)
知识点1 全等图形
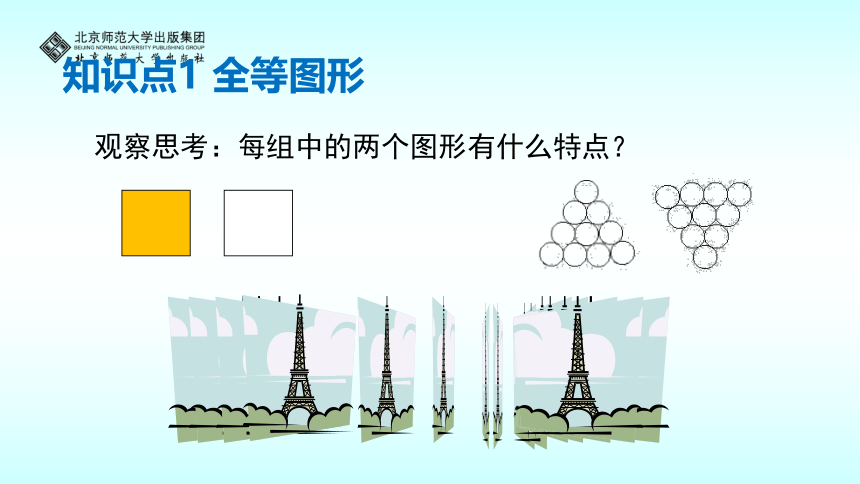
观察思考:每组中的两个图形有什么特点?
知识点1 全等图形
全等图形的概念
能够完全重合的两个图形称为全等图形
(1)全等图形与图形的位置无关,唯一标准就是可以完全重合。
(2)图形经平移、旋转、翻折后只改变了位置,没改变形状与大小,能与原图形完全重合。
全等图形的特征
全等图形的形状和大小都相同
注意
知识点1 全等图形
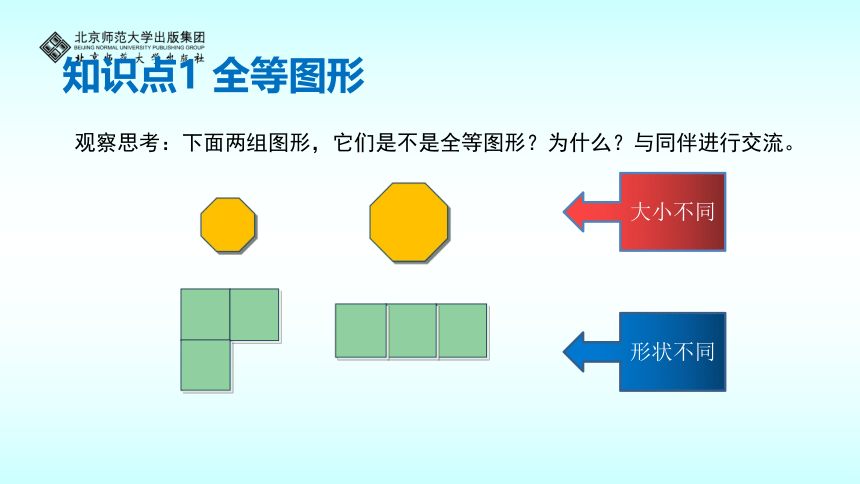
观察思考:下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
大小不同
形状不同
知识点1 全等图形
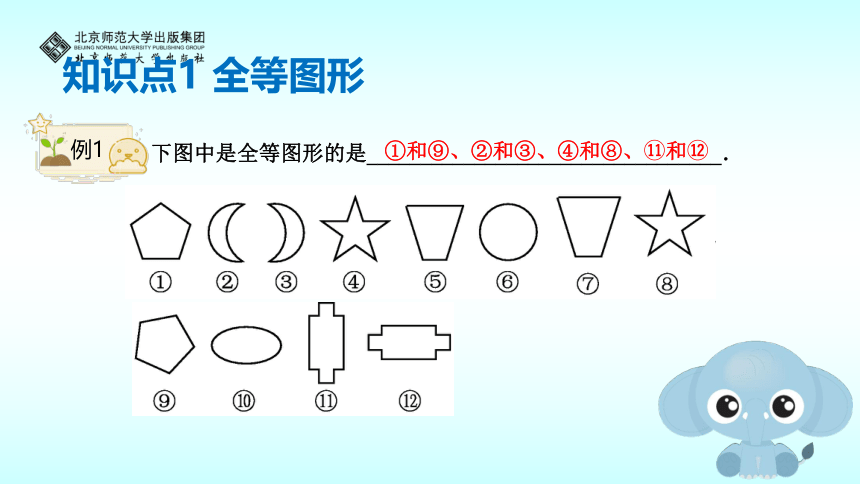
下图中是全等图形的是_________________________________.
①和⑨、②和③、④和⑧、?和?
例1
知识点1 全等图形
下列说法中正确的有( )
①用一张底片冲洗出来的10张1寸相片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形是全等图形;
④全等图形的面积一定相等.
A.1个 B.2个 C.3个 D.4个
C
例2
知识点2 全等三角形的概念及表示方法
A
B
C
E
D
F
能够完全重合的两个三角形,叫做全等三角形.
形状相同
大小相等
D
E
F
A
B
C
知识点2 全等三角形的概念及表示方法
对应关系
对应顶点
对应边
对应角
△ABC ≌ △DEF
全等于
≌
知识点2 全等三角形的概念及表示方法
A
B
C
D
E
F
对应关系
≌
△ABC ≌ △DEF
知识点2 全等三角形的概念及表示方法
C
A
B
F
E
D
全等
01
找出对应顶点
02
确定字母顺序
△ABC
≌
△DEF
字母顺序必须对应
关于△ACB全等的三角形是 。
△DFE
知识点2 全等三角形的概念及表示方法
D
B
O
C
A
如图,△OCA和△OBD,下列哪种表示全等的说法是正确的?
A.△OCA≌△ODB
B.△OCA≌△OBD
C.△OAC≌△OBD
D.△AOC≌△BOD
例3
知识点2 全等三角形的概念及表示方法
跟踪练习
如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,∠AOD与∠AOE.
知识点3 全等三角形的性质
性质:全等三角形的对应边相等,对应角相等
∵△ABC≌△DEF,
∴AB=DE,AC=DF ,BC=EF ,(全等三角形的对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E .(全等三角形的对应角相等)
几何语言:
A
B
C
D
E
F
知识点3 全等三角形的性质
头脑风暴:全等三角形对应边的高、中线相等吗?你还能找出全等三角形的其他性质吗?
全等三角形对应边上的中线相等,对应边上的高相等,对应角平分线相等;全等三角形的周长相等、面积也相等.
知识点3 全等三角形的性质
例4
如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长
解:∵△ABC≌△DEF,∠B=50°,
∴∠DEF=∠B=50°(全等三角形的对应角相等)
∵BF=4,EF=7,
∴BC=EF=7(全等三角形的对应边相等)
CF=BC-BF=7-4=3.
知识点3 全等三角形的性质
例4
如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长
追问:观察图形中线段的数量或位置关系,你能否试着提出一个正确的结论并证明它呢?
数量关系:EC=BF
位置关系:DE∥AB,AC∥DF
如图,正方形ABCD沿AM翻折,使D点落在BC上的N点处,如果AD=7cm,DM=5cm,∠DAM=39°,则AN= cm,NM= cm,∠NAB= .
知识点3 全等三角形的性质
7
5
12°
????
?
????
?
????
?
????
?
????
?
????
?
5cm
)39°
7cm
例5
)39°
3
知识点3 全等三角形的性质
如图,将长方形纸片ABCD沿BD折叠,得到△BC’D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
A.20° B.30°
C.35° D.55°
变式
4
5
6
3
4
A
巩固提升
1、如图,点E是CD上一点,Rt△ADC≌Rt△CEB,∠D=90°,则下列结论:①AC=BC,②AD∥BE,③∠ACB=90°,④AD+DE=BE,其中正确的有 。
A
C
D
B
E
∟
∟
∟
1
2
3
①②③④
巩固提升
2、如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC,DE相交于点F,求∠DFB的度数。
A
B
C
O
D
F
E
解:∵△ABC≌△ADE
∴∠B=∠D,∠BAC=∠DAE
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE
∵∠BAD+∠CAE=∠BAE-∠DAC=100°-60°=40°
∴∠BAD=20°
∵∠D+∠DFB+∠DOF=∠B+∠BAD+∠BOA=180°
又∵∠DOF=∠BOA
∴∠DFB=∠BAO=20°
课堂小结
图形的全等
全等图形
全等三角形的
概念及表示方法
全等三角形的
性质
能够完全重合的两个图形称为全等图形
全等图形的形状和大小都相同
对应顶点的字母写在对应位置上
对应边相等;对应角相等
数学知识
思想方法
模型思想
8字模型
随堂练习
1、判断正误:
(1)两个面积相等的图形一定是全等图形 ( )
(2)两个长方形是全等图形 ( )
(3)两个全等图形形状一定相同 ( )
(4)两个正方形一定是全等图形 ( )
×
×
×
√
随堂练习
2、下列四组图形中,是全等图形的一组是( )
D
随堂练习
3、如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD是对应角,且∠BAC=25°,∠B=35°,AB=3cm,BC=1cm,求出∠E, ∠ ADE的度数和线段DE,AE 的长度.
B
C
E
D
A
解:∵ △ABC≌△AED,∠BAC=25°,∠B=35°,AB=3cm,BC=1cm
∴∠E= ∠B= 35°(全等三角形对应角相等)
∠ADE=∠ACB=180°-25°-35°=120 °(全等三角形对应角相等)
DE=BC=1cm, AE=AB=3cm(全等三角形对应边相等)
课后作业
必做题:课本78、79页习题3.5
选做题:如图,△ABC≌△AEF中,给出下列结论:①∠AFC=∠AFE;②BF=DE:③∠BFE=∠BAE;④∠BFD=∠CAF.其中正确的结论是 .(填写所正确结论的序号).
1.了解全等图形的概念,会判断两个图形是不是全等图形.
2.理解全等三角形的概念,能正确表示全等三角形,能识别全等三角形中的对应边、对应角.(难点)
3.掌握全等三角形的性质,能利用全等三角形的性质解决相关问题.(重点)
学习目标
知识点1 全等图形
思考:观察下面各组图形,它们有什么共同特点?
(1)
(2)
(3)
(4)
知识点1 全等图形
追问 你能再举出生活中的一些类似例子吗?
(5)
(6)
(7)
知识点1 全等图形
观察思考:每组中的两个图形有什么特点?
知识点1 全等图形
全等图形的概念
能够完全重合的两个图形称为全等图形
(1)全等图形与图形的位置无关,唯一标准就是可以完全重合。
(2)图形经平移、旋转、翻折后只改变了位置,没改变形状与大小,能与原图形完全重合。
全等图形的特征
全等图形的形状和大小都相同
注意
知识点1 全等图形
观察思考:下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
大小不同
形状不同
知识点1 全等图形
下图中是全等图形的是_________________________________.
①和⑨、②和③、④和⑧、?和?
例1
知识点1 全等图形
下列说法中正确的有( )
①用一张底片冲洗出来的10张1寸相片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形是全等图形;
④全等图形的面积一定相等.
A.1个 B.2个 C.3个 D.4个
C
例2
知识点2 全等三角形的概念及表示方法
A
B
C
E
D
F
能够完全重合的两个三角形,叫做全等三角形.
形状相同
大小相等
D
E
F
A
B
C
知识点2 全等三角形的概念及表示方法
对应关系
对应顶点
对应边
对应角
△ABC ≌ △DEF
全等于
≌
知识点2 全等三角形的概念及表示方法
A
B
C
D
E
F
对应关系
≌
△ABC ≌ △DEF
知识点2 全等三角形的概念及表示方法
C
A
B
F
E
D
全等
01
找出对应顶点
02
确定字母顺序
△ABC
≌
△DEF
字母顺序必须对应
关于△ACB全等的三角形是 。
△DFE
知识点2 全等三角形的概念及表示方法
D
B
O
C
A
如图,△OCA和△OBD,下列哪种表示全等的说法是正确的?
A.△OCA≌△ODB
B.△OCA≌△OBD
C.△OAC≌△OBD
D.△AOC≌△BOD
例3
知识点2 全等三角形的概念及表示方法
跟踪练习
如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,∠AOD与∠AOE.
知识点3 全等三角形的性质
性质:全等三角形的对应边相等,对应角相等
∵△ABC≌△DEF,
∴AB=DE,AC=DF ,BC=EF ,(全等三角形的对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E .(全等三角形的对应角相等)
几何语言:
A
B
C
D
E
F
知识点3 全等三角形的性质
头脑风暴:全等三角形对应边的高、中线相等吗?你还能找出全等三角形的其他性质吗?
全等三角形对应边上的中线相等,对应边上的高相等,对应角平分线相等;全等三角形的周长相等、面积也相等.
知识点3 全等三角形的性质
例4
如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长
解:∵△ABC≌△DEF,∠B=50°,
∴∠DEF=∠B=50°(全等三角形的对应角相等)
∵BF=4,EF=7,
∴BC=EF=7(全等三角形的对应边相等)
CF=BC-BF=7-4=3.
知识点3 全等三角形的性质
例4
如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长
追问:观察图形中线段的数量或位置关系,你能否试着提出一个正确的结论并证明它呢?
数量关系:EC=BF
位置关系:DE∥AB,AC∥DF
如图,正方形ABCD沿AM翻折,使D点落在BC上的N点处,如果AD=7cm,DM=5cm,∠DAM=39°,则AN= cm,NM= cm,∠NAB= .
知识点3 全等三角形的性质
7
5
12°
????
?
????
?
????
?
????
?
????
?
????
?
5cm
)39°
7cm
例5
)39°
3
知识点3 全等三角形的性质
如图,将长方形纸片ABCD沿BD折叠,得到△BC’D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
A.20° B.30°
C.35° D.55°
变式
4
5
6
3
4
A
巩固提升
1、如图,点E是CD上一点,Rt△ADC≌Rt△CEB,∠D=90°,则下列结论:①AC=BC,②AD∥BE,③∠ACB=90°,④AD+DE=BE,其中正确的有 。
A
C
D
B
E
∟
∟
∟
1
2
3
①②③④
巩固提升
2、如图,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC,DE相交于点F,求∠DFB的度数。
A
B
C
O
D
F
E
解:∵△ABC≌△ADE
∴∠B=∠D,∠BAC=∠DAE
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE
∵∠BAD+∠CAE=∠BAE-∠DAC=100°-60°=40°
∴∠BAD=20°
∵∠D+∠DFB+∠DOF=∠B+∠BAD+∠BOA=180°
又∵∠DOF=∠BOA
∴∠DFB=∠BAO=20°
课堂小结
图形的全等
全等图形
全等三角形的
概念及表示方法
全等三角形的
性质
能够完全重合的两个图形称为全等图形
全等图形的形状和大小都相同
对应顶点的字母写在对应位置上
对应边相等;对应角相等
数学知识
思想方法
模型思想
8字模型
随堂练习
1、判断正误:
(1)两个面积相等的图形一定是全等图形 ( )
(2)两个长方形是全等图形 ( )
(3)两个全等图形形状一定相同 ( )
(4)两个正方形一定是全等图形 ( )
×
×
×
√
随堂练习
2、下列四组图形中,是全等图形的一组是( )
D
随堂练习
3、如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD是对应角,且∠BAC=25°,∠B=35°,AB=3cm,BC=1cm,求出∠E, ∠ ADE的度数和线段DE,AE 的长度.
B
C
E
D
A
解:∵ △ABC≌△AED,∠BAC=25°,∠B=35°,AB=3cm,BC=1cm
∴∠E= ∠B= 35°(全等三角形对应角相等)
∠ADE=∠ACB=180°-25°-35°=120 °(全等三角形对应角相等)
DE=BC=1cm, AE=AB=3cm(全等三角形对应边相等)
课后作业
必做题:课本78、79页习题3.5
选做题:如图,△ABC≌△AEF中,给出下列结论:①∠AFC=∠AFE;②BF=DE:③∠BFE=∠BAE;④∠BFD=∠CAF.其中正确的结论是 .(填写所正确结论的序号).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
