北师大版九下数学3.5确定圆的条件课件(共66张PPT)
文档属性
| 名称 | 北师大版九下数学3.5确定圆的条件课件(共66张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览









文档简介
(共66张PPT)
第三章 圆
初中数学(北师大版)
九年级 下册
知识点一 确定圆的条件
1.确定圆的条件
不在同一条直线上的三个点确定一个圆.
注意 (1)“不在同一条直线上”这个条件不可忽略.
(2)“确定”一词可理解为“有且只有”,即不仅能作圆,而且只能作一个圆.
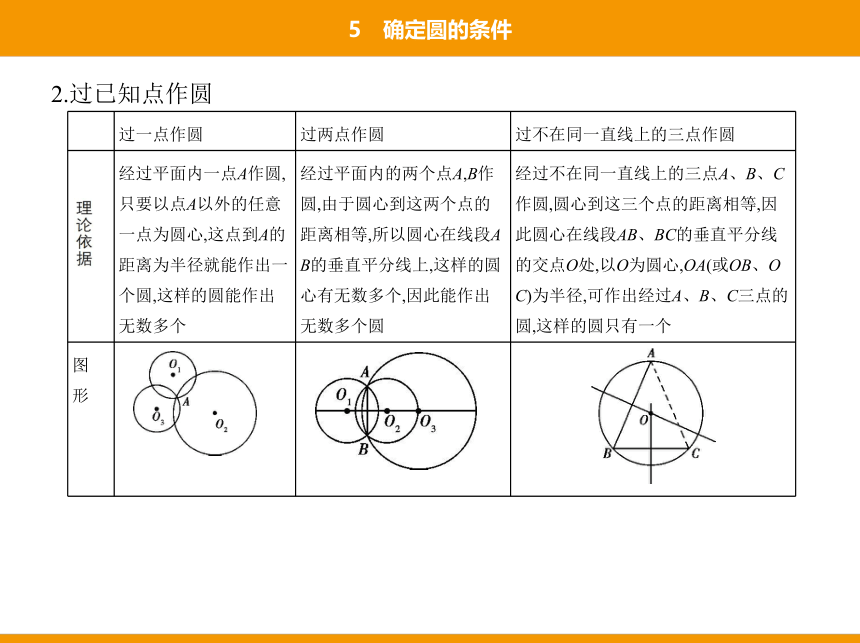
2.过已知点作圆
过一点作圆 过两点作圆 过不在同一直线上的三点作圆
经过平面内一点A作圆,只要以点A以外的任意一点为圆心,这点到A的距离为半径就能作出一个圆,这样的圆能作出无数多个 经过平面内的两个点A,B作圆,由于圆心到这两个点的距离相等,所以圆心在线段AB的垂直平分线上,这样的圆心有无数多个,因此能作出无数多个圆 经过不在同一直线上的三点A、B、C作圆,圆心到这三个点的距离相等,因此圆心在线段AB、BC的垂直平分线的交点O处,以O为圆心,OA(或OB、OC)为半径,可作出经过A、B、C三点的圆,这样的圆只有一个
图 形
3.判断过任意四点能否作圆:
过任意四点不一定能作出圆,要想过四点作圆,应先作出经过不在同一条直
线上的三点的圆,若第四个点到圆心的距离等于半径,则第四个点在圆上,
否则不在圆上.过任意四点能不能作圆也可以根据四点所围成的四边形是
否满足对角互补来判断,若对角互补,则过这四个点能作一个圆;若对角不
互补,则过这四个点不能作圆.
例1 如图3-5-1所示的是一个残破的车轮,现要做一个与原来一模一样的
车轮,试确定车轮外圆的大小.
图3-5-1
分析 本题主要考查圆的确定方法.这是一道实际应用题,只要在残破的车
轮的圆周上找到不共线的三点,分别作任意两点所连线段的中垂线,其交点
即为车轮外圆的圆心,圆心到车轮圆周上任意一点的距离均为半径,由此可
确定车轮外圆的大小.
解析 在残破的车轮的圆周上任取不共线的三点A,B,C,连接AB、BC,分别
作AB,BC的中垂线,这两条中垂线必交于一点O,以O为圆心、OA的长为半
径作圆,即可确定原车轮外圆的大小.
点拨 “三个点确定一个圆”这一结论成立的前提条件是“三点不在同
一直线上”.
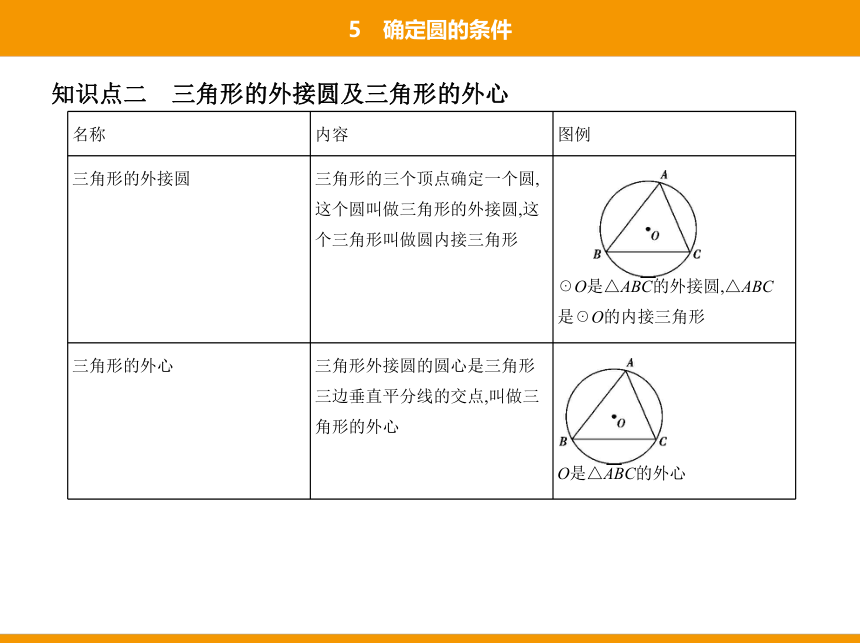
知识点二 三角形的外接圆及三角形的外心
名称 内容 图例
三角形的外接圆 三角形的三个顶点确定一个圆,
这个圆叫做三角形的外接圆,这
个三角形叫做圆内接三角形
☉O是△ABC的外接圆,△ABC
是☉O的内接三角形
三角形的外心 三角形外接圆的圆心是三角形
三边垂直平分线的交点,叫做三
角形的外心
O是△ABC的外心
拓展延伸 一个三角形有唯一确定的外接圆,一个圆有无数个内接三角形;
任意一个圆都有内接多边形,但不是所有的多边形都有外接圆,例如:菱形
(非正方形)就没有外接圆.由于锐角三角形三边的垂直平分线的交点在三角形的内部,故锐角三角形的外心在三角形的内部;由于直角三角形三边的垂直平分线的交点就是斜边的中点,故直角三角形的外心就是斜边的中点;类似地,可以得出钝角三角形的外心在三角形的外部.由三角形的外心与三角形的位置关系也可以确定三角形的形状.如图3-5-2,分别作出锐角三角形、直角三角形、钝角三角形的外接圆,点O为外接圆的圆心,即外心.
图3-5-2
例2 如图3-5-3,△ABC是☉O的内接等边三角形,其边长为6,求这个三角形
的外接圆的半径.
图3-5-3
解析 如图3-5-4,连接OA,过点O作OD⊥AB于点D.
∵△ABC是等边三角形,
∴AO平分∠BAC,且∠BAC=60°,
∴∠DAO=30°.
∵OD⊥AB,∴AD= AB=3.
图3-5-4
在Rt△DAO中,由∠DAO=30°,得OD= OA.由勾股定理,得OA2=OD2+AD2,
∴OA2= OA2+9,解得OA=2 (负值不符合题意,舍去).
∴这个三角形的外接圆的半径是2 .
温馨提示 求三角形的外接圆的半径时,最常用的办法:连接圆心与三角形
的顶点(即半径),过圆心向三角形的一边作垂线,构造一个直角三角形,将求
半径问题转化为求直角三角形中斜边长的问题.等边三角形的外心既是三
边中垂线的交点,也是三条内角平分线的交点.
题型一 利用三角形外接圆和圆周角的性质解决实际问题
例1 如图3-5-5,小明家的房前有一块空地,空地上有三棵树A、B、C,小明
想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若在△ABC中,AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
图3-5-5
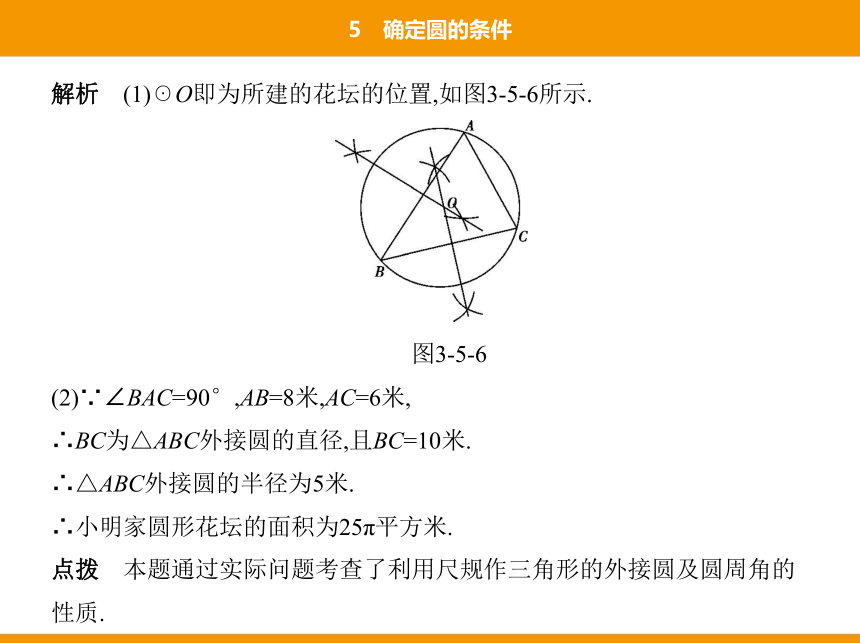
解析 (1)☉O即为所建的花坛的位置,如图3-5-6所示.
图3-5-6
(2)∵∠BAC=90°,AB=8米,AC=6米,
∴BC为△ABC外接圆的直径,且BC=10米.
∴△ABC外接圆的半径为5米.
∴小明家圆形花坛的面积为25π平方米.
点拨 本题通过实际问题考查了利用尺规作三角形的外接圆及圆周角的
性质.
题型二 与三角形外接圆有关的计算
例2 已知△ABC中,AC=10,BC=8,AB=6,求△ABC外接圆的半径.
分析 因为6,8,10是一组勾股数,所以△ABC为直角三角形.直角三角形外
接圆的圆心为直角三角形的斜边中点,半径等于斜边的一半.
解析 ∵BC2+AB2=82+62=100,AC2=102=100,∴BC2+AB2=AC2.
∴△ABC为直角三角形,
∴Rt△ABC的外接圆的圆心是斜边AC的中点.
∴Rt△ABC的外接圆的半径R= AC=5,
即△ABC外接圆的半径为5.
点拨 直角三角形的外接圆是以斜边中点为圆心,斜边长的一半为半径的
圆.
知识点一 确定圆的条件
1.如图3-5-1,点A、B、C在同一条直线上,点D在直线外,过这四点中的任意
3个点,能画圆的个数是 ( )
图3-5-1
A.1 B.2 C.3 D.4
答案 C 从A、B、C三点中任取两点,有3种情况,这3种情况中的每一种
情况都与点D构成不在同一直线上的三点,故能画出3个圆.
2.小明不慎把家里的一块圆形玻璃打碎了,其中四块碎片如图3-5-2所示,为
配到一块与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应
该是 ( )
图3-5-2
A.第①块 B.第②块 C.第③块 D.第④块
答案 A 要配到与原来大小一样的圆形玻璃,关键是确定圆心的位置和
半径.小明带到商店去的一块玻璃碎片应该是第①块,可以在第①块碎片的
圆弧上取两点,连接这两点得到一条弦,然后作这条弦的垂直平分线,同样,
再作另一条弦的垂直平分线,两条垂直平分线的交点即为圆心,从而确定半
径,该圆即可确定.
3.某市有A,B,C三个居民生活小区,一个购物超市P及两个游乐场.已知三个
居民生活小区及两个游乐场到购物超市的距离都相等,并且A,B两个居民
生活小区到两个游乐场的距离也分别相等,试在图3-5-3中确定游乐场的位置.
图3-5-3
解析 (1)连接AB,BC;
(2)作AB的垂直平分线EF,作BC的垂直平分线GH,EF交GH于点P;
(3)连接PA,以P为圆心,PA的长为半径作☉P,☉P交直线EF于M,N两点.
M,N两点即为游乐场的位置,如图.
知识点二 三角形的外接圆及三角形的外心
4.下列说法中,正确的个数是 ( )
①任何三角形有且只有一个外接圆;②任何圆有且只有一个内接三角形;
③三角形的外心不一定在三角形内部;④三角形的外心到三角形三边的距
离相等;⑤经过三点可确定一个圆.
A.1 B.2 C.3 D.4
答案 B ①③正确.任何一个圆都有无数个内接三角形,故②错;三角形的
外心到三角形的三个顶点的距离相等,故④错;经过不在同一直线上的三点
可确定一个圆,故⑤错.
5.(2019江苏扬州高邮期中)如图3-5-4,在锐角△ABC中,∠A=45°,BC=2 cm,
能够将△ABC完全覆盖的最小圆形纸片的直径是 cm.
图3-5-4
答案 2
解析 如图,以AB为直径作圆,则∠ACB=90°,△ABC为等腰直角三角形.过
C作CH⊥AB,交于点O,连接BH,则CH为圆的直径.由圆周角定理的推论得
∠H=∠A=45°,∠HBC=90°,∴CH= BC=2 (cm).
6.在直角坐标系中,已知点A(0,4)、B(4,4)和C(6,2).
(1)点A、B、C能确定一个圆吗 说明理由;
(2)如果能,用尺规作图的方法画出过这三点的圆的轨迹;
(3)写出圆心P的坐标,并求出☉P的半径.
解析 (1)点A、B、C能确定一个圆,理由:点A、B、C不在同一条直线上.
(2)如图:
(3)由AB的垂直平分线,BC的垂直平分线的交点,得
圆心P的坐标是(2,0),则半径的长为 =2 .
1.下列说法不正确的是 ( )
A.经过一个点的圆有无数个
B.经过两个点的圆有无数个
C.经过不在同一条直线上的三个点可确定一个圆
D.过四个点一定能作一个圆
答案 D 由作圆方法可知A、B、C均正确,而过四个点不一定能作圆,如
这四个点在同一条直线上,故D错误.故选D.
2.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△
ABC外接圆的圆心坐标是 ( )
A.(2,3) B.(3,2)
C.(1,3) D.(3,1)
答案 D 作线段AB和线段AC的垂直平分线,两线的交点(3,1)即为外接圆
的圆心.
3.已知线段AB=6 cm,则过A、B两点的最小圆的半径为 cm,过A、
B两点 (填“有”或“无”)最大圆.
答案 3;无
解析 过A、B两点的最小圆是以线段AB为直径的圆;过A、B两点的圆有
无数个,没有最大圆.
4.如图,O为△ABC的外心,若∠BAC=70°,则∠OBC的度数为 .
答案 20°
解析 ∵O为△ABC的外心,
∴∠BOC=2∠BAC=2×70°=140°.
∵OB=OC,∴∠OBC=∠OCB= =20°.
5.已知,如图,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,
∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)当点D是△ABC外接圆的圆心时,请判断四边形BDCE的形状,并证明你
的结论.
解析 (1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBD=∠DBE+∠CBD,
∴∠ABD=∠CBE,
在△ABD与△CBE中,∵
∴△ABD≌△CBE.
(2)四边形BDCE是菱形.证明:
同(1)可证△ABD≌△CBE,∴AD=CE,
∵点D是△ABC外接圆的圆心,∴DA=DB=DC,又∵BD=BE,∴BD=BE=CE=
CD,∴四边形BDCE是菱形.
1.(2018江苏镇江模拟)如图3-5-5,已知平面直角坐标系内三点A(3,0)、B(5,
0)、C(0,4),☉P经过点A、B、C,则点P的坐标为 ( )
图3-5-5
A.(6,8) B.(4,5) C. D.
答案 C ∵☉P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),如图,连接AP,PC,作PE⊥OB于E,PF⊥OC于F,由题意
得, = ,解得y= ,故选C.
2.如图3-5-6,在坐标平面上,△ABC为直角三角形,∠B=90°,AB垂直于x轴,M
为△ABC的外心.若点A的坐标为(3,4),点M的坐标为(-1,1),则点B的坐标为
.
图3-5-6
答案 (3,-2)
解析 ∵M为△ABC的外心,△ABC为直角三角形,∴M为AC的中点,又∵点
A的坐标为(3,4),点M的坐标为(-1,1),∴点C的坐标为(-5,-2).∵△ABC为直角
三角形,∴BC∥x轴,∴点B的坐标为(3,-2).
3.已知点O为△ABC的外心,且∠BOC=100°,试求∠BAC的度数.
解析 如图①,当△ABC为锐角三角形时,点O在△ABC的内部,则∠BAC=
∠BOC=50°;
如图②,当△ABC为直角三角形时,点O在△ABC的斜边上,则∠BAC= ∠
BOC=50°;
如图③,当△ABC为钝角三角形时,点O在△ABC的外部,则∠BAC=180°-
∠BOC=130°.
综上可知,∠BAC的度数为50°或130°.
1.平面直角坐标系内的三个点A(1,0)、B(0,-3)、C(2,-3) 确定一个
圆(填“能”或“不能”).
答案 能
解析 在平面直角坐标系内描点或利用一次函数的知识可知这三个点不
在同一直线上,所以这三个点能确定一个圆.
2.如图,△ABC是☉O的内接三角形,直径GH⊥AB,交AC于点D,GH,BC的延
长线相交于点E.
(1)求证:∠OAD=∠E;
(2)若OD=1,DE=3,试求☉O的半径.
解析 (1)证明:连接OB,如图.
∵直径GH⊥AB,∴ = ,
∴∠AOG=∠GOB= ∠AOB.
∵∠ACB= ∠AOB,∴∠AOG=∠ACB,∴∠AOD=∠DCE.
又∵∠ADO=∠CDE,∴∠OAD=∠E. (2)连接OC,如图.
∵OC=OA,∴∠OAD=∠OCA.由(1)知∠OAD=∠E,∴∠OCD=∠E.
又∵∠DOC=∠COE,∴△OCD∽△OEC,∴ = ,
∴OC2=OE·OD=(1+3)×1=4,∴OC=2,即☉O的半径为2.
3.等边三角形的边长为a,求这个三角形外接圆的面积.
解析 如图,连接AO,过点O作OD⊥AB于点D,
∵AB=AC=BC,∴AO平分∠BAC,
∴∠DAO= ∠BAC= ×60°=30°.
∵OD⊥AB,AB=a,∴AD= AB= a,
在Rt△AOD中,AO= = = a.
∴☉O的面积为π = πa2.
4.(2019浙江杭州模拟)如图,木工师傅在板材边角处作直角时,往往使用
“三弧法”,其作法如下:①作线段AB,分别以A,B为圆心,AB长为半径作弧,
两弧的交点为C;②以C为圆心,仍以AB长为半径作弧,交AC的延长线于
点D;③连接BD,BC.根据以上作法完成以下问题:
(1)求∠CBD的度数;
(2)试说明sin2A+sin2D=1的理由.
解析 (1)由作法可知AC=AB=BC,
∴△ABC是等边三角形,∴∠A=∠ACB=60°,∵CD=CB,∴∠D=∠CBD,
∵∠ACB=∠D+∠CBD,∴∠CBD=∠D=30°.
(2)∵∠A=60°,∠D=30°,
∴sin2A=sin260°= = ,sin2D=sin230°= ,∴sin2A+sin2D=1.
一、选择题
1.(2019浙江杭州下城期中,5,★☆☆)给定下列条件可以确定一个圆的是
( )
A.已知圆心 B.已知半径
C.已知直径 D.不在同一直线上的三点
答案 D 仅知道圆心、半径或直径都不能确定一个圆;不在同一直线上
的三点可以确定一个圆,故D符合题意.故选D.
2.(2019河北唐山路南三模,6,★★☆)如图3-5-7,O为锐角三角形ABC的外
心,四边形OCDE为正方形,其中E点在△ABC的外部,下列叙述不正确的是
( )
图3-5-7
A.O是△AEB的外心,O不是△AED的外心
B.O是△BEC的外心,O不是△BCD的外心
C.O是△AEC的外心,O不是△BCD的外心
D.O是△ADB的外心,O不是△ADC的外心
答案 D 如图,连接OB、OD、OA,
∵O为锐角三角形ABC的外心,
∴OA=OC=OB,
∵四边形OCDE为正方形,
∴OE=OC∴OA=OB=OC=OE≠OD.
OB=OE=OC,即O是△BEC的外心,
OB=OC≠OD,即O不是△BCD的外心,
OA=OE≠OD,即O不是△AED的外心,
OA=OE=OB,即O是△AEB的外心,
OA=OC=OE,即O是△ACE的外心,
OB=OA≠OD,即O不是△ABD的外心,
OA=OC≠OD,即O不是△ADC的外心.故选D.
二、填空题
3.(2017江苏盐城大丰期中,16,★☆☆)已知直角三角形的两直角边长分别
为5、12,则它的外接圆的直径为 .
答案 13
解析 由勾股定理得直角三角形的斜边长为 =13,则它的外接圆的
直径为13.
1.(2019陕西渭南白水一模,9,★☆☆)如图,已知O是△ABC的外接圆,直径
AD=4,∠ABC=∠DAC,则AC的长为 ( )
A.2 B.2 C.4 D.4
答案 A 连接CD,如图所示.
∵AD是☉O的直径,∴∠ACD=90°,
∵∠ADC=∠ABC,∠ABC=∠DAC,∴∠ADC=∠DAC,
∴AC=DC,△ACD是等腰直角三角形,
∴AD= AC,∴AC= = =2 .
2.(2019河北保定高阳模拟,11,★☆☆)如图,在△ABC中,∠A=60°,BC=5 cm,
能够将△ABC完全覆盖的最小圆形纸片的直径是 ( )
A.5 cm B. cm C.10 cm D. cm
答案 D 能够将△ABC完全覆盖的最小圆是△ABC的外接圆,设圆心为
点O,连接OB,OC,如图所示.
∵在△ABC中,∠A=60°,BC=5 cm,∴∠BOC=120°,
作OD⊥BC于点D,则∠ODB=90°,∠BOD=60°,
∴BD= cm,∠OBD=30°,∴OB= = cm,
∴2OB= cm,即能够将△ABC完全覆盖的最小圆形纸片的直径是 cm.
3.(2019河南南阳社旗一模,9,★★☆)如图,在已知的△ABC中,按以下步骤
操作:(1)分别以B、C为圆心,大于 BC的长为半径作弧,两弧相交于M、N;
(2)作直线MN,交AB于D,连接CD.若CD=AD,∠B=20°,则下列结论:①∠ADC=40°;②∠ACD=70°;③点D为△ABC的外心;④∠ACD=90°,其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
答案 B 由题意可知,直线MN是线段BC的垂直平分线,∴BD=CD,∠B=
∠BCD=20°,∴∠ADC=∠BCD+∠CBD=40°,故①正确;∵CD=AD,∴∠A=
∠ACD,又∵∠A+∠ACD+∠ADC=180°,∴∠ACD=70°,故②正确,④错误;∵AD=CD,BD=CD,∴AD=BD=CD,∴D是△ABC的外心,故③正确.
4.(2019山东济南平阳一模,12,★★☆)如图,等边△ABC的边长为4,点O是△
ABC的外心,∠FOG=120°.绕点O旋转∠FOG,分别交线段AB、BC于D、E
两点.连接DE,给出下列四个结论:①OD=OE;②S△ODE=S△BDE;③S四边形ODBE=
;④△BDE周长的最小值为4.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
答案 B 如图,连接OB,OC,过点D作DM⊥BC于M.
∵等边△ABC的边长为4,点O是△ABC的外心,∠FOG=120°,∴易证∠BOD
=∠COE,OB=OC,∠DBO=∠ECO=30°,∴△BOD≌△COE,∴OD=OE,故①
正确;
当D与B重合时,E与C重合,此时S△ODE>0,而△BDE不存在,故②错误;
∵△BOD≌△COE,∴S四边形ODBE=S△ODB+S△BOE=S△OCE+S△BOE=S△BOC= S△ABC= ,
故③正确;
∵△BOD≌△COE,∴BD=EC,∴△BDE的周长=BD+BE+DE=BC+DE,∵BC
=4,∴当DE最小时,△BDE的周长最小,设BD=x,则BM= x,DM= x,EC=BD
=x,BE=4-x,
∴ME=BE-BM=4- x,∴由勾股定理得DE= =
= ,
∴当x=2时,DE的最小值为2,
∴△BDE周长的最小值为6,故④错误.所以①③正确.
一、选择题
1.(2018四川自贡中考,9,★☆☆)如图3-5-8,若△ABC内接于半径为R的☉O,
且∠A=60°,连接OB、OC,则边BC的长为( )
图3-5-8
A. R B. R C. R D. R
答案 D 如图,延长BO交☉O于D,连接CD,则∠BCD=90°,∠D=∠A=60°,
在Rt△BCD中,∵BD=2R,∴BC=BD·sin 60°= R,故选D.
二、填空题
2.(2019湖南衡阳中考,17,★★☆)已知圆的半径是6,则圆内接正三角形的
边长是 .
答案 6
解析 如图,连接OA,OB,作OC⊥AB于点C,则OA=OB,∠AOB=360°÷3=120
°,∴∠AOC=60°,∴AC=OA×sin 60°=6× =3 ,∴AB=2AC=6 .
3.(2019四川雅安中考,20,★★☆)如图3-5-9,△ABC内接于☉O,BD是☉O的
直径,∠CBD=21°,则∠A的度数为 .
图3-5-9
答案 69°
解析 ∵BD是☉O的直径,∴∠BCD=90°,∵△ABC内接于☉O,∠CBD=21
°,∴∠A=∠D=90°-21°=69°.
三、解答题
4.(2017山东临沂中考,23,★★☆)如图3-5-10,∠BAC的平分线交△ABC的
外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
图3-5-10
解析 (1)证明:∵AD平分∠BAC,∴∠BAD=∠CAD.
又∵∠CBD=∠CAD,∴∠BAD=∠CBD.
∵BE平分∠ABC,∴∠CBE=∠ABE,
∴∠DBE=∠CBE+∠CBD=∠ABE+∠BAD.
又∵∠BED=∠ABE+∠BAD,∴∠DBE=∠BED,
∴DE=DB.
(2)连接CD,∵∠BAC=90°,∴BC是直径,
∴∠BDC=90°,∵AD平分∠BAC,
∴ = ,∴BD=CD=4,∴BC= =4 .
∴△ABC外接圆的半径为2 .
5.(2019北京中考,22,★★☆)在平面内,给定不在同一条直线上的点A,B,C,
如图3-5-11所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等
于a的所有点组成图形G,∠ABC的平分线交图形G于点D,连接AD,CD.
(1)求证:AD=CD;
(2)过点D作DE⊥BA,垂足为E,作DF⊥BC,垂足为F,延长DF交图形G于点M,
连接CM.若AD=CM,求直线DE与图形G的公共点个数.
图3-5-11
解析 (1)证明:∵到点O的距离等于a的所有点组成图形G,∴图形G为△
ABC的外接圆,∵BD平分∠ABC,
∴∠ABD=∠CBD,∴ = ,∴AD=CD.
(2)如图,连接OD.
∵AD=CM,AD=CD,∴CD=CM,∵DM⊥BC,∴BC垂直平分DM,∵BC为直径,
∴∠BAC=90°,∵ = ,∴OD⊥AC,∴OD∥AB,∵DE⊥BE,∴OD⊥DE,∴
DE为☉O的切线,∴直线DE与图形G的公共点个数为1.
1.(2019四川乐山中考,10,★★☆)如图,抛物线y= x2-4与x轴交于A、B两点,
P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,
则OQ的最大值是 ( )
A.3 B. C. D.4
答案 C 连接BP,如图,
当y=0时, x2-4=0,解得x1=4,x2=-4,则A(-4,0),B(4,0),∵Q是线段PA的中点,∴
OQ为△ABP的中位线,∴OQ= BP,∴当BP最大时,OQ最大,而BP过圆心C
时,PB最大,如图,点P运动到P'位置时,BP最大.∵BC= =5,∴BP'=5+2=
7,∴OQ的最大值是 .故选C.
2.(2019江苏连云港中考,8,★★☆)如图,在矩形ABCD中,AD=2 AB.将矩
形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交
点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为
G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③
PC= MP;④BP= AB;⑤点F是△CMP外接圆的圆心,其中正确的个数为
( )
A.2个 B.3个 C.4个 D.5个
答案 B ∵沿着CM折叠,点D的对应点为E,
∴∠DMC=∠EMC,
∵沿着MP折叠,AM与EM重合,折痕为MP,
∴∠AMP=∠EMP,
∵∠AMD=180°,∴∠PME+∠CME= ×180°=90°,
∴△CMP是直角三角形,故①正确;
∵沿着CM折叠,点D的对应点为E,
∴∠D=∠MEC=90°,
∵沿着MP折叠,AM与EM重合,折痕为MP,
∴∠MEG=∠A=90°,
∴∠GEC=180°,
∴点C、E、G在同一条直线上,故②错误;
∵AD=2 AB,
∴设AB=x,则AD=2 x,
∵将矩形ABCD对折,得到折痕MN,
∴DM= AD= x,
∴CM= = x,
∵∠PMC=90°,MN⊥PC,
∴CM2=CN·CP,
∴CP= = x,
∴PN=CP-CN= x,∴PM= = x,
∴ = = ,
∴PC= MP,故③错误;
∵PC= x,∴PB=2 x- x= x,
∴ = ,∴PB= AB,故④正确;
∵CD=CE,EG=AB,AB=CD,∴CE=EG,
∵∠CEM=∠G=90°,
∴FE∥PG,∴CF=PF,
∵∠PMC=90°,∴CF=PF=MF,
∴点F是△CMP外接圆的圆心,故⑤正确.故选B.
3.(2019黑龙江绥化中考,20,★★☆)半径为5的☉O是锐角三角形ABC的外
接圆,AB=AC,连接OB、OC,延长CO交弦AB于点D.若△OBD是直角三角形,
则弦BC的长为 .
答案 5 或5
解析 如图,当∠ODB=90°,即CD⊥AB时,
AD=BD,∴AC=BC,∵AB=AC,∴△ABC是等边三角形,
∴∠DBO=30°,∵OB=5,∴BD= OB= ,
∴BC=AB=5 .
如图,当∠DOB=90°时,∠BOC=90°,
∴△BOC是等腰直角三角形,
∴BC= OB=5 .
综上所述,弦BC的长为5 或5 .
1.探究问题:
(1)阅读理解:
①如图3-5-12(A),在△ABC所在平面上存在一点P,若它到△ABC三个顶点
的距离之和最小,则称点P为△ABC的费马点,此时PA+PB+PC的值为△
ABC的费马距离.
②如图3-5-12(B),若四边形ABCD的四个顶点在同一个圆上,则有AB·CD+
BC·DA=AC·BD,此为托勒密定理.
图3-5-12
(2)知识迁移:
①请你利用托勒密定理解决如下问题:
如图3-5-12(C),已知点P为等边△ABC外接圆的 上任意一点.求证:PB+
PC=PA;
②根据(2)①的结论,我们有如下探寻△ABC(其中∠A、∠B、∠C均小于1
20°)的费马点和费马距离的方法:
第一步:如图3-5-12(D),在△ABC的外部以BC为一边作等边△BCD及其外
接圆;
第二步:在 上任取一点P',连接P'A、P'B、P'C、P'D.易知P'A+P'B+P'C=P'
A+(P'B+P'C)=P'A+ ;
第三步:请你根据(1)①中定义,在图3-5-12(D)中找出△ABC的费马点P,则线
段 的长度即为△ABC的费马距离.
(3)知识应用:
今年以来某市持续干旱,许多村庄出现了人、畜饮水困难的问题,为解决老
百姓的饮水问题,解放军某部来到该市某地打井取水.
已知三村庄A、B、C构成了如图3-5-12(E)所示的△ABC(其中∠A、∠B、
∠C均小于120°),现选取一点P打水井,使从水井P到三村庄A、B、C所铺设
的输水管总长度最小,求输水管总长度的最小值.
解析 (2)①证明:由托勒密定理可知PB·AC+PC·AB=PA·BC.
∵△ABC是等边三角形,
∴AB=AC=BC,∴PB+PC=PA.
②P'D;AD.点P的位置如图所示(AD与 的交点).
(3)以BC为一边作如图所示的等边△BCD,连接AD,则线段AD的长即为△
ABC的费马距离.
∵△BCD为等边三角形,BC=4 km,
∴∠CBD=60°,BD=BC=4 km.
∵∠ABC=30°,∴∠ABD=90°.
在Rt△ABD中,∵AB=3 km,BD=4 km,
∴AD= = =5(km).
∴从水井P到三村庄A、B、C所铺设的输水管总长度的最小值为5 km.
2.(2018福建龙岩新罗期中)阅读材料回答问题.
命题:如图3-5-13①,在锐角△ABC中,BC=a,CA=b,AB=c,△ABC的外接圆半
径为R,则 = = =2R.
证明:连接CO,并延长交☉O于点D,连接DB,则∠D=∠A.
∵CD为☉O的直径,∴∠DBC=90°.
在Rt△BDC中,sin D= = ,
∴sin A= ,即 =2R.
同理可证 = =2R.∴ = = =2R.
请你阅读上面所给的命题及其证明,完成下面的(1)(2)两小题.
图3-5-13
(1)上面的阅读材料中略去了“ =2R”和“ =2R”的证明过程,请
你把“ =2R”的证明过程补写出来;
(2)直接用上面阅读材料中命题的结论解题:
已知,如图3-5-13②,在锐角△ABC中,BC= ,CA= ,∠A=60°,求△ABC的
外接圆半径R及∠C.
解析 (1)证明:如图,连接AO,并延长交☉O于点E,连接EC,则∠E=∠B.
∵AE为☉O的直径,∴∠ECA=90°.
在Rt△ECA中,sin E= = ,∴sin B= ,∴ =2R.
(2)a= ,b= ,∠A=60°.
由命题的结论知 = ,∴sin B= ,∴∠B=45°,
∴∠C=180°-60°-45°=75°.∵ =2R,∴R=1.
如图,矩形ABCD中,E为AB的中点,有一圆过C、D、E三点,且此圆分别与
AD、BC相交于点P、Q.甲、乙两人想找到此圆的圆心O,其作法如下:甲:
作∠DEC的平分线l,作DE的中垂线,交l于O点,则O即为所求;乙:连接PC、
QD,两线段交于一点O,则O即为所求.对于甲、乙两人的作法,下列判断正
确的是 ( )
A.两人的作法皆正确
B.两人的作法皆错误
C.甲的作法正确,乙的作法错误
D.甲的作法错误,乙的作法正确
答案 A 甲的作法中,∵E为AB的中点,
∴ED=EC,∴△DEC为等腰三角形,
又l为∠DEC的平分线,∴l为CD的中垂线,
∴O为两条中垂线的交点,即O为△CDE的外心,
∴O为此圆的圆心.
乙的作法中,∵∠ADC=90°,∠DCB=90°,
∴PC、QD为此圆的直径,
∴PC与QD的交点O为此圆的圆心,因此甲、乙两人的作法皆正确.故选A.
第三章 圆
初中数学(北师大版)
九年级 下册
知识点一 确定圆的条件
1.确定圆的条件
不在同一条直线上的三个点确定一个圆.
注意 (1)“不在同一条直线上”这个条件不可忽略.
(2)“确定”一词可理解为“有且只有”,即不仅能作圆,而且只能作一个圆.
2.过已知点作圆
过一点作圆 过两点作圆 过不在同一直线上的三点作圆
经过平面内一点A作圆,只要以点A以外的任意一点为圆心,这点到A的距离为半径就能作出一个圆,这样的圆能作出无数多个 经过平面内的两个点A,B作圆,由于圆心到这两个点的距离相等,所以圆心在线段AB的垂直平分线上,这样的圆心有无数多个,因此能作出无数多个圆 经过不在同一直线上的三点A、B、C作圆,圆心到这三个点的距离相等,因此圆心在线段AB、BC的垂直平分线的交点O处,以O为圆心,OA(或OB、OC)为半径,可作出经过A、B、C三点的圆,这样的圆只有一个
图 形
3.判断过任意四点能否作圆:
过任意四点不一定能作出圆,要想过四点作圆,应先作出经过不在同一条直
线上的三点的圆,若第四个点到圆心的距离等于半径,则第四个点在圆上,
否则不在圆上.过任意四点能不能作圆也可以根据四点所围成的四边形是
否满足对角互补来判断,若对角互补,则过这四个点能作一个圆;若对角不
互补,则过这四个点不能作圆.
例1 如图3-5-1所示的是一个残破的车轮,现要做一个与原来一模一样的
车轮,试确定车轮外圆的大小.
图3-5-1
分析 本题主要考查圆的确定方法.这是一道实际应用题,只要在残破的车
轮的圆周上找到不共线的三点,分别作任意两点所连线段的中垂线,其交点
即为车轮外圆的圆心,圆心到车轮圆周上任意一点的距离均为半径,由此可
确定车轮外圆的大小.
解析 在残破的车轮的圆周上任取不共线的三点A,B,C,连接AB、BC,分别
作AB,BC的中垂线,这两条中垂线必交于一点O,以O为圆心、OA的长为半
径作圆,即可确定原车轮外圆的大小.
点拨 “三个点确定一个圆”这一结论成立的前提条件是“三点不在同
一直线上”.
知识点二 三角形的外接圆及三角形的外心
名称 内容 图例
三角形的外接圆 三角形的三个顶点确定一个圆,
这个圆叫做三角形的外接圆,这
个三角形叫做圆内接三角形
☉O是△ABC的外接圆,△ABC
是☉O的内接三角形
三角形的外心 三角形外接圆的圆心是三角形
三边垂直平分线的交点,叫做三
角形的外心
O是△ABC的外心
拓展延伸 一个三角形有唯一确定的外接圆,一个圆有无数个内接三角形;
任意一个圆都有内接多边形,但不是所有的多边形都有外接圆,例如:菱形
(非正方形)就没有外接圆.由于锐角三角形三边的垂直平分线的交点在三角形的内部,故锐角三角形的外心在三角形的内部;由于直角三角形三边的垂直平分线的交点就是斜边的中点,故直角三角形的外心就是斜边的中点;类似地,可以得出钝角三角形的外心在三角形的外部.由三角形的外心与三角形的位置关系也可以确定三角形的形状.如图3-5-2,分别作出锐角三角形、直角三角形、钝角三角形的外接圆,点O为外接圆的圆心,即外心.
图3-5-2
例2 如图3-5-3,△ABC是☉O的内接等边三角形,其边长为6,求这个三角形
的外接圆的半径.
图3-5-3
解析 如图3-5-4,连接OA,过点O作OD⊥AB于点D.
∵△ABC是等边三角形,
∴AO平分∠BAC,且∠BAC=60°,
∴∠DAO=30°.
∵OD⊥AB,∴AD= AB=3.
图3-5-4
在Rt△DAO中,由∠DAO=30°,得OD= OA.由勾股定理,得OA2=OD2+AD2,
∴OA2= OA2+9,解得OA=2 (负值不符合题意,舍去).
∴这个三角形的外接圆的半径是2 .
温馨提示 求三角形的外接圆的半径时,最常用的办法:连接圆心与三角形
的顶点(即半径),过圆心向三角形的一边作垂线,构造一个直角三角形,将求
半径问题转化为求直角三角形中斜边长的问题.等边三角形的外心既是三
边中垂线的交点,也是三条内角平分线的交点.
题型一 利用三角形外接圆和圆周角的性质解决实际问题
例1 如图3-5-5,小明家的房前有一块空地,空地上有三棵树A、B、C,小明
想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若在△ABC中,AB=8米,AC=6米,∠BAC=90°,试求小明家圆形花坛的面积.
图3-5-5
解析 (1)☉O即为所建的花坛的位置,如图3-5-6所示.
图3-5-6
(2)∵∠BAC=90°,AB=8米,AC=6米,
∴BC为△ABC外接圆的直径,且BC=10米.
∴△ABC外接圆的半径为5米.
∴小明家圆形花坛的面积为25π平方米.
点拨 本题通过实际问题考查了利用尺规作三角形的外接圆及圆周角的
性质.
题型二 与三角形外接圆有关的计算
例2 已知△ABC中,AC=10,BC=8,AB=6,求△ABC外接圆的半径.
分析 因为6,8,10是一组勾股数,所以△ABC为直角三角形.直角三角形外
接圆的圆心为直角三角形的斜边中点,半径等于斜边的一半.
解析 ∵BC2+AB2=82+62=100,AC2=102=100,∴BC2+AB2=AC2.
∴△ABC为直角三角形,
∴Rt△ABC的外接圆的圆心是斜边AC的中点.
∴Rt△ABC的外接圆的半径R= AC=5,
即△ABC外接圆的半径为5.
点拨 直角三角形的外接圆是以斜边中点为圆心,斜边长的一半为半径的
圆.
知识点一 确定圆的条件
1.如图3-5-1,点A、B、C在同一条直线上,点D在直线外,过这四点中的任意
3个点,能画圆的个数是 ( )
图3-5-1
A.1 B.2 C.3 D.4
答案 C 从A、B、C三点中任取两点,有3种情况,这3种情况中的每一种
情况都与点D构成不在同一直线上的三点,故能画出3个圆.
2.小明不慎把家里的一块圆形玻璃打碎了,其中四块碎片如图3-5-2所示,为
配到一块与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应
该是 ( )
图3-5-2
A.第①块 B.第②块 C.第③块 D.第④块
答案 A 要配到与原来大小一样的圆形玻璃,关键是确定圆心的位置和
半径.小明带到商店去的一块玻璃碎片应该是第①块,可以在第①块碎片的
圆弧上取两点,连接这两点得到一条弦,然后作这条弦的垂直平分线,同样,
再作另一条弦的垂直平分线,两条垂直平分线的交点即为圆心,从而确定半
径,该圆即可确定.
3.某市有A,B,C三个居民生活小区,一个购物超市P及两个游乐场.已知三个
居民生活小区及两个游乐场到购物超市的距离都相等,并且A,B两个居民
生活小区到两个游乐场的距离也分别相等,试在图3-5-3中确定游乐场的位置.
图3-5-3
解析 (1)连接AB,BC;
(2)作AB的垂直平分线EF,作BC的垂直平分线GH,EF交GH于点P;
(3)连接PA,以P为圆心,PA的长为半径作☉P,☉P交直线EF于M,N两点.
M,N两点即为游乐场的位置,如图.
知识点二 三角形的外接圆及三角形的外心
4.下列说法中,正确的个数是 ( )
①任何三角形有且只有一个外接圆;②任何圆有且只有一个内接三角形;
③三角形的外心不一定在三角形内部;④三角形的外心到三角形三边的距
离相等;⑤经过三点可确定一个圆.
A.1 B.2 C.3 D.4
答案 B ①③正确.任何一个圆都有无数个内接三角形,故②错;三角形的
外心到三角形的三个顶点的距离相等,故④错;经过不在同一直线上的三点
可确定一个圆,故⑤错.
5.(2019江苏扬州高邮期中)如图3-5-4,在锐角△ABC中,∠A=45°,BC=2 cm,
能够将△ABC完全覆盖的最小圆形纸片的直径是 cm.
图3-5-4
答案 2
解析 如图,以AB为直径作圆,则∠ACB=90°,△ABC为等腰直角三角形.过
C作CH⊥AB,交于点O,连接BH,则CH为圆的直径.由圆周角定理的推论得
∠H=∠A=45°,∠HBC=90°,∴CH= BC=2 (cm).
6.在直角坐标系中,已知点A(0,4)、B(4,4)和C(6,2).
(1)点A、B、C能确定一个圆吗 说明理由;
(2)如果能,用尺规作图的方法画出过这三点的圆的轨迹;
(3)写出圆心P的坐标,并求出☉P的半径.
解析 (1)点A、B、C能确定一个圆,理由:点A、B、C不在同一条直线上.
(2)如图:
(3)由AB的垂直平分线,BC的垂直平分线的交点,得
圆心P的坐标是(2,0),则半径的长为 =2 .
1.下列说法不正确的是 ( )
A.经过一个点的圆有无数个
B.经过两个点的圆有无数个
C.经过不在同一条直线上的三个点可确定一个圆
D.过四个点一定能作一个圆
答案 D 由作圆方法可知A、B、C均正确,而过四个点不一定能作圆,如
这四个点在同一条直线上,故D错误.故选D.
2.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△
ABC外接圆的圆心坐标是 ( )
A.(2,3) B.(3,2)
C.(1,3) D.(3,1)
答案 D 作线段AB和线段AC的垂直平分线,两线的交点(3,1)即为外接圆
的圆心.
3.已知线段AB=6 cm,则过A、B两点的最小圆的半径为 cm,过A、
B两点 (填“有”或“无”)最大圆.
答案 3;无
解析 过A、B两点的最小圆是以线段AB为直径的圆;过A、B两点的圆有
无数个,没有最大圆.
4.如图,O为△ABC的外心,若∠BAC=70°,则∠OBC的度数为 .
答案 20°
解析 ∵O为△ABC的外心,
∴∠BOC=2∠BAC=2×70°=140°.
∵OB=OC,∴∠OBC=∠OCB= =20°.
5.已知,如图,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,
∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)当点D是△ABC外接圆的圆心时,请判断四边形BDCE的形状,并证明你
的结论.
解析 (1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBD=∠DBE+∠CBD,
∴∠ABD=∠CBE,
在△ABD与△CBE中,∵
∴△ABD≌△CBE.
(2)四边形BDCE是菱形.证明:
同(1)可证△ABD≌△CBE,∴AD=CE,
∵点D是△ABC外接圆的圆心,∴DA=DB=DC,又∵BD=BE,∴BD=BE=CE=
CD,∴四边形BDCE是菱形.
1.(2018江苏镇江模拟)如图3-5-5,已知平面直角坐标系内三点A(3,0)、B(5,
0)、C(0,4),☉P经过点A、B、C,则点P的坐标为 ( )
图3-5-5
A.(6,8) B.(4,5) C. D.
答案 C ∵☉P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),如图,连接AP,PC,作PE⊥OB于E,PF⊥OC于F,由题意
得, = ,解得y= ,故选C.
2.如图3-5-6,在坐标平面上,△ABC为直角三角形,∠B=90°,AB垂直于x轴,M
为△ABC的外心.若点A的坐标为(3,4),点M的坐标为(-1,1),则点B的坐标为
.
图3-5-6
答案 (3,-2)
解析 ∵M为△ABC的外心,△ABC为直角三角形,∴M为AC的中点,又∵点
A的坐标为(3,4),点M的坐标为(-1,1),∴点C的坐标为(-5,-2).∵△ABC为直角
三角形,∴BC∥x轴,∴点B的坐标为(3,-2).
3.已知点O为△ABC的外心,且∠BOC=100°,试求∠BAC的度数.
解析 如图①,当△ABC为锐角三角形时,点O在△ABC的内部,则∠BAC=
∠BOC=50°;
如图②,当△ABC为直角三角形时,点O在△ABC的斜边上,则∠BAC= ∠
BOC=50°;
如图③,当△ABC为钝角三角形时,点O在△ABC的外部,则∠BAC=180°-
∠BOC=130°.
综上可知,∠BAC的度数为50°或130°.
1.平面直角坐标系内的三个点A(1,0)、B(0,-3)、C(2,-3) 确定一个
圆(填“能”或“不能”).
答案 能
解析 在平面直角坐标系内描点或利用一次函数的知识可知这三个点不
在同一直线上,所以这三个点能确定一个圆.
2.如图,△ABC是☉O的内接三角形,直径GH⊥AB,交AC于点D,GH,BC的延
长线相交于点E.
(1)求证:∠OAD=∠E;
(2)若OD=1,DE=3,试求☉O的半径.
解析 (1)证明:连接OB,如图.
∵直径GH⊥AB,∴ = ,
∴∠AOG=∠GOB= ∠AOB.
∵∠ACB= ∠AOB,∴∠AOG=∠ACB,∴∠AOD=∠DCE.
又∵∠ADO=∠CDE,∴∠OAD=∠E. (2)连接OC,如图.
∵OC=OA,∴∠OAD=∠OCA.由(1)知∠OAD=∠E,∴∠OCD=∠E.
又∵∠DOC=∠COE,∴△OCD∽△OEC,∴ = ,
∴OC2=OE·OD=(1+3)×1=4,∴OC=2,即☉O的半径为2.
3.等边三角形的边长为a,求这个三角形外接圆的面积.
解析 如图,连接AO,过点O作OD⊥AB于点D,
∵AB=AC=BC,∴AO平分∠BAC,
∴∠DAO= ∠BAC= ×60°=30°.
∵OD⊥AB,AB=a,∴AD= AB= a,
在Rt△AOD中,AO= = = a.
∴☉O的面积为π = πa2.
4.(2019浙江杭州模拟)如图,木工师傅在板材边角处作直角时,往往使用
“三弧法”,其作法如下:①作线段AB,分别以A,B为圆心,AB长为半径作弧,
两弧的交点为C;②以C为圆心,仍以AB长为半径作弧,交AC的延长线于
点D;③连接BD,BC.根据以上作法完成以下问题:
(1)求∠CBD的度数;
(2)试说明sin2A+sin2D=1的理由.
解析 (1)由作法可知AC=AB=BC,
∴△ABC是等边三角形,∴∠A=∠ACB=60°,∵CD=CB,∴∠D=∠CBD,
∵∠ACB=∠D+∠CBD,∴∠CBD=∠D=30°.
(2)∵∠A=60°,∠D=30°,
∴sin2A=sin260°= = ,sin2D=sin230°= ,∴sin2A+sin2D=1.
一、选择题
1.(2019浙江杭州下城期中,5,★☆☆)给定下列条件可以确定一个圆的是
( )
A.已知圆心 B.已知半径
C.已知直径 D.不在同一直线上的三点
答案 D 仅知道圆心、半径或直径都不能确定一个圆;不在同一直线上
的三点可以确定一个圆,故D符合题意.故选D.
2.(2019河北唐山路南三模,6,★★☆)如图3-5-7,O为锐角三角形ABC的外
心,四边形OCDE为正方形,其中E点在△ABC的外部,下列叙述不正确的是
( )
图3-5-7
A.O是△AEB的外心,O不是△AED的外心
B.O是△BEC的外心,O不是△BCD的外心
C.O是△AEC的外心,O不是△BCD的外心
D.O是△ADB的外心,O不是△ADC的外心
答案 D 如图,连接OB、OD、OA,
∵O为锐角三角形ABC的外心,
∴OA=OC=OB,
∵四边形OCDE为正方形,
∴OE=OC
OB=OE=OC,即O是△BEC的外心,
OB=OC≠OD,即O不是△BCD的外心,
OA=OE≠OD,即O不是△AED的外心,
OA=OE=OB,即O是△AEB的外心,
OA=OC=OE,即O是△ACE的外心,
OB=OA≠OD,即O不是△ABD的外心,
OA=OC≠OD,即O不是△ADC的外心.故选D.
二、填空题
3.(2017江苏盐城大丰期中,16,★☆☆)已知直角三角形的两直角边长分别
为5、12,则它的外接圆的直径为 .
答案 13
解析 由勾股定理得直角三角形的斜边长为 =13,则它的外接圆的
直径为13.
1.(2019陕西渭南白水一模,9,★☆☆)如图,已知O是△ABC的外接圆,直径
AD=4,∠ABC=∠DAC,则AC的长为 ( )
A.2 B.2 C.4 D.4
答案 A 连接CD,如图所示.
∵AD是☉O的直径,∴∠ACD=90°,
∵∠ADC=∠ABC,∠ABC=∠DAC,∴∠ADC=∠DAC,
∴AC=DC,△ACD是等腰直角三角形,
∴AD= AC,∴AC= = =2 .
2.(2019河北保定高阳模拟,11,★☆☆)如图,在△ABC中,∠A=60°,BC=5 cm,
能够将△ABC完全覆盖的最小圆形纸片的直径是 ( )
A.5 cm B. cm C.10 cm D. cm
答案 D 能够将△ABC完全覆盖的最小圆是△ABC的外接圆,设圆心为
点O,连接OB,OC,如图所示.
∵在△ABC中,∠A=60°,BC=5 cm,∴∠BOC=120°,
作OD⊥BC于点D,则∠ODB=90°,∠BOD=60°,
∴BD= cm,∠OBD=30°,∴OB= = cm,
∴2OB= cm,即能够将△ABC完全覆盖的最小圆形纸片的直径是 cm.
3.(2019河南南阳社旗一模,9,★★☆)如图,在已知的△ABC中,按以下步骤
操作:(1)分别以B、C为圆心,大于 BC的长为半径作弧,两弧相交于M、N;
(2)作直线MN,交AB于D,连接CD.若CD=AD,∠B=20°,则下列结论:①∠ADC=40°;②∠ACD=70°;③点D为△ABC的外心;④∠ACD=90°,其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
答案 B 由题意可知,直线MN是线段BC的垂直平分线,∴BD=CD,∠B=
∠BCD=20°,∴∠ADC=∠BCD+∠CBD=40°,故①正确;∵CD=AD,∴∠A=
∠ACD,又∵∠A+∠ACD+∠ADC=180°,∴∠ACD=70°,故②正确,④错误;∵AD=CD,BD=CD,∴AD=BD=CD,∴D是△ABC的外心,故③正确.
4.(2019山东济南平阳一模,12,★★☆)如图,等边△ABC的边长为4,点O是△
ABC的外心,∠FOG=120°.绕点O旋转∠FOG,分别交线段AB、BC于D、E
两点.连接DE,给出下列四个结论:①OD=OE;②S△ODE=S△BDE;③S四边形ODBE=
;④△BDE周长的最小值为4.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
答案 B 如图,连接OB,OC,过点D作DM⊥BC于M.
∵等边△ABC的边长为4,点O是△ABC的外心,∠FOG=120°,∴易证∠BOD
=∠COE,OB=OC,∠DBO=∠ECO=30°,∴△BOD≌△COE,∴OD=OE,故①
正确;
当D与B重合时,E与C重合,此时S△ODE>0,而△BDE不存在,故②错误;
∵△BOD≌△COE,∴S四边形ODBE=S△ODB+S△BOE=S△OCE+S△BOE=S△BOC= S△ABC= ,
故③正确;
∵△BOD≌△COE,∴BD=EC,∴△BDE的周长=BD+BE+DE=BC+DE,∵BC
=4,∴当DE最小时,△BDE的周长最小,设BD=x,则BM= x,DM= x,EC=BD
=x,BE=4-x,
∴ME=BE-BM=4- x,∴由勾股定理得DE= =
= ,
∴当x=2时,DE的最小值为2,
∴△BDE周长的最小值为6,故④错误.所以①③正确.
一、选择题
1.(2018四川自贡中考,9,★☆☆)如图3-5-8,若△ABC内接于半径为R的☉O,
且∠A=60°,连接OB、OC,则边BC的长为( )
图3-5-8
A. R B. R C. R D. R
答案 D 如图,延长BO交☉O于D,连接CD,则∠BCD=90°,∠D=∠A=60°,
在Rt△BCD中,∵BD=2R,∴BC=BD·sin 60°= R,故选D.
二、填空题
2.(2019湖南衡阳中考,17,★★☆)已知圆的半径是6,则圆内接正三角形的
边长是 .
答案 6
解析 如图,连接OA,OB,作OC⊥AB于点C,则OA=OB,∠AOB=360°÷3=120
°,∴∠AOC=60°,∴AC=OA×sin 60°=6× =3 ,∴AB=2AC=6 .
3.(2019四川雅安中考,20,★★☆)如图3-5-9,△ABC内接于☉O,BD是☉O的
直径,∠CBD=21°,则∠A的度数为 .
图3-5-9
答案 69°
解析 ∵BD是☉O的直径,∴∠BCD=90°,∵△ABC内接于☉O,∠CBD=21
°,∴∠A=∠D=90°-21°=69°.
三、解答题
4.(2017山东临沂中考,23,★★☆)如图3-5-10,∠BAC的平分线交△ABC的
外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
图3-5-10
解析 (1)证明:∵AD平分∠BAC,∴∠BAD=∠CAD.
又∵∠CBD=∠CAD,∴∠BAD=∠CBD.
∵BE平分∠ABC,∴∠CBE=∠ABE,
∴∠DBE=∠CBE+∠CBD=∠ABE+∠BAD.
又∵∠BED=∠ABE+∠BAD,∴∠DBE=∠BED,
∴DE=DB.
(2)连接CD,∵∠BAC=90°,∴BC是直径,
∴∠BDC=90°,∵AD平分∠BAC,
∴ = ,∴BD=CD=4,∴BC= =4 .
∴△ABC外接圆的半径为2 .
5.(2019北京中考,22,★★☆)在平面内,给定不在同一条直线上的点A,B,C,
如图3-5-11所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等
于a的所有点组成图形G,∠ABC的平分线交图形G于点D,连接AD,CD.
(1)求证:AD=CD;
(2)过点D作DE⊥BA,垂足为E,作DF⊥BC,垂足为F,延长DF交图形G于点M,
连接CM.若AD=CM,求直线DE与图形G的公共点个数.
图3-5-11
解析 (1)证明:∵到点O的距离等于a的所有点组成图形G,∴图形G为△
ABC的外接圆,∵BD平分∠ABC,
∴∠ABD=∠CBD,∴ = ,∴AD=CD.
(2)如图,连接OD.
∵AD=CM,AD=CD,∴CD=CM,∵DM⊥BC,∴BC垂直平分DM,∵BC为直径,
∴∠BAC=90°,∵ = ,∴OD⊥AC,∴OD∥AB,∵DE⊥BE,∴OD⊥DE,∴
DE为☉O的切线,∴直线DE与图形G的公共点个数为1.
1.(2019四川乐山中考,10,★★☆)如图,抛物线y= x2-4与x轴交于A、B两点,
P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,
则OQ的最大值是 ( )
A.3 B. C. D.4
答案 C 连接BP,如图,
当y=0时, x2-4=0,解得x1=4,x2=-4,则A(-4,0),B(4,0),∵Q是线段PA的中点,∴
OQ为△ABP的中位线,∴OQ= BP,∴当BP最大时,OQ最大,而BP过圆心C
时,PB最大,如图,点P运动到P'位置时,BP最大.∵BC= =5,∴BP'=5+2=
7,∴OQ的最大值是 .故选C.
2.(2019江苏连云港中考,8,★★☆)如图,在矩形ABCD中,AD=2 AB.将矩
形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交
点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为
G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③
PC= MP;④BP= AB;⑤点F是△CMP外接圆的圆心,其中正确的个数为
( )
A.2个 B.3个 C.4个 D.5个
答案 B ∵沿着CM折叠,点D的对应点为E,
∴∠DMC=∠EMC,
∵沿着MP折叠,AM与EM重合,折痕为MP,
∴∠AMP=∠EMP,
∵∠AMD=180°,∴∠PME+∠CME= ×180°=90°,
∴△CMP是直角三角形,故①正确;
∵沿着CM折叠,点D的对应点为E,
∴∠D=∠MEC=90°,
∵沿着MP折叠,AM与EM重合,折痕为MP,
∴∠MEG=∠A=90°,
∴∠GEC=180°,
∴点C、E、G在同一条直线上,故②错误;
∵AD=2 AB,
∴设AB=x,则AD=2 x,
∵将矩形ABCD对折,得到折痕MN,
∴DM= AD= x,
∴CM= = x,
∵∠PMC=90°,MN⊥PC,
∴CM2=CN·CP,
∴CP= = x,
∴PN=CP-CN= x,∴PM= = x,
∴ = = ,
∴PC= MP,故③错误;
∵PC= x,∴PB=2 x- x= x,
∴ = ,∴PB= AB,故④正确;
∵CD=CE,EG=AB,AB=CD,∴CE=EG,
∵∠CEM=∠G=90°,
∴FE∥PG,∴CF=PF,
∵∠PMC=90°,∴CF=PF=MF,
∴点F是△CMP外接圆的圆心,故⑤正确.故选B.
3.(2019黑龙江绥化中考,20,★★☆)半径为5的☉O是锐角三角形ABC的外
接圆,AB=AC,连接OB、OC,延长CO交弦AB于点D.若△OBD是直角三角形,
则弦BC的长为 .
答案 5 或5
解析 如图,当∠ODB=90°,即CD⊥AB时,
AD=BD,∴AC=BC,∵AB=AC,∴△ABC是等边三角形,
∴∠DBO=30°,∵OB=5,∴BD= OB= ,
∴BC=AB=5 .
如图,当∠DOB=90°时,∠BOC=90°,
∴△BOC是等腰直角三角形,
∴BC= OB=5 .
综上所述,弦BC的长为5 或5 .
1.探究问题:
(1)阅读理解:
①如图3-5-12(A),在△ABC所在平面上存在一点P,若它到△ABC三个顶点
的距离之和最小,则称点P为△ABC的费马点,此时PA+PB+PC的值为△
ABC的费马距离.
②如图3-5-12(B),若四边形ABCD的四个顶点在同一个圆上,则有AB·CD+
BC·DA=AC·BD,此为托勒密定理.
图3-5-12
(2)知识迁移:
①请你利用托勒密定理解决如下问题:
如图3-5-12(C),已知点P为等边△ABC外接圆的 上任意一点.求证:PB+
PC=PA;
②根据(2)①的结论,我们有如下探寻△ABC(其中∠A、∠B、∠C均小于1
20°)的费马点和费马距离的方法:
第一步:如图3-5-12(D),在△ABC的外部以BC为一边作等边△BCD及其外
接圆;
第二步:在 上任取一点P',连接P'A、P'B、P'C、P'D.易知P'A+P'B+P'C=P'
A+(P'B+P'C)=P'A+ ;
第三步:请你根据(1)①中定义,在图3-5-12(D)中找出△ABC的费马点P,则线
段 的长度即为△ABC的费马距离.
(3)知识应用:
今年以来某市持续干旱,许多村庄出现了人、畜饮水困难的问题,为解决老
百姓的饮水问题,解放军某部来到该市某地打井取水.
已知三村庄A、B、C构成了如图3-5-12(E)所示的△ABC(其中∠A、∠B、
∠C均小于120°),现选取一点P打水井,使从水井P到三村庄A、B、C所铺设
的输水管总长度最小,求输水管总长度的最小值.
解析 (2)①证明:由托勒密定理可知PB·AC+PC·AB=PA·BC.
∵△ABC是等边三角形,
∴AB=AC=BC,∴PB+PC=PA.
②P'D;AD.点P的位置如图所示(AD与 的交点).
(3)以BC为一边作如图所示的等边△BCD,连接AD,则线段AD的长即为△
ABC的费马距离.
∵△BCD为等边三角形,BC=4 km,
∴∠CBD=60°,BD=BC=4 km.
∵∠ABC=30°,∴∠ABD=90°.
在Rt△ABD中,∵AB=3 km,BD=4 km,
∴AD= = =5(km).
∴从水井P到三村庄A、B、C所铺设的输水管总长度的最小值为5 km.
2.(2018福建龙岩新罗期中)阅读材料回答问题.
命题:如图3-5-13①,在锐角△ABC中,BC=a,CA=b,AB=c,△ABC的外接圆半
径为R,则 = = =2R.
证明:连接CO,并延长交☉O于点D,连接DB,则∠D=∠A.
∵CD为☉O的直径,∴∠DBC=90°.
在Rt△BDC中,sin D= = ,
∴sin A= ,即 =2R.
同理可证 = =2R.∴ = = =2R.
请你阅读上面所给的命题及其证明,完成下面的(1)(2)两小题.
图3-5-13
(1)上面的阅读材料中略去了“ =2R”和“ =2R”的证明过程,请
你把“ =2R”的证明过程补写出来;
(2)直接用上面阅读材料中命题的结论解题:
已知,如图3-5-13②,在锐角△ABC中,BC= ,CA= ,∠A=60°,求△ABC的
外接圆半径R及∠C.
解析 (1)证明:如图,连接AO,并延长交☉O于点E,连接EC,则∠E=∠B.
∵AE为☉O的直径,∴∠ECA=90°.
在Rt△ECA中,sin E= = ,∴sin B= ,∴ =2R.
(2)a= ,b= ,∠A=60°.
由命题的结论知 = ,∴sin B= ,∴∠B=45°,
∴∠C=180°-60°-45°=75°.∵ =2R,∴R=1.
如图,矩形ABCD中,E为AB的中点,有一圆过C、D、E三点,且此圆分别与
AD、BC相交于点P、Q.甲、乙两人想找到此圆的圆心O,其作法如下:甲:
作∠DEC的平分线l,作DE的中垂线,交l于O点,则O即为所求;乙:连接PC、
QD,两线段交于一点O,则O即为所求.对于甲、乙两人的作法,下列判断正
确的是 ( )
A.两人的作法皆正确
B.两人的作法皆错误
C.甲的作法正确,乙的作法错误
D.甲的作法错误,乙的作法正确
答案 A 甲的作法中,∵E为AB的中点,
∴ED=EC,∴△DEC为等腰三角形,
又l为∠DEC的平分线,∴l为CD的中垂线,
∴O为两条中垂线的交点,即O为△CDE的外心,
∴O为此圆的圆心.
乙的作法中,∵∠ADC=90°,∠DCB=90°,
∴PC、QD为此圆的直径,
∴PC与QD的交点O为此圆的圆心,因此甲、乙两人的作法皆正确.故选A.
