北师大版七年级数学下册 4.1认识三角形 第2课时 三角形的三边关系课件 (共21张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.1认识三角形 第2课时 三角形的三边关系课件 (共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 792.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览




文档简介
1 认识三角形
第2课时 三角形的三边关系
第四章 三角形
学习目标
1.掌握三角形按边分类方法,能够判定三角形
是否为特殊的三角形;
2.探索并掌握三角形三边之间的关系,能够运用三角形的
三边关系解决问题.(难点)
数学来源于生活,生活中处处有数学.观察下面的图片,你发现了什么?
问:你能不能给三角形下一个完整的定义?
情境导入
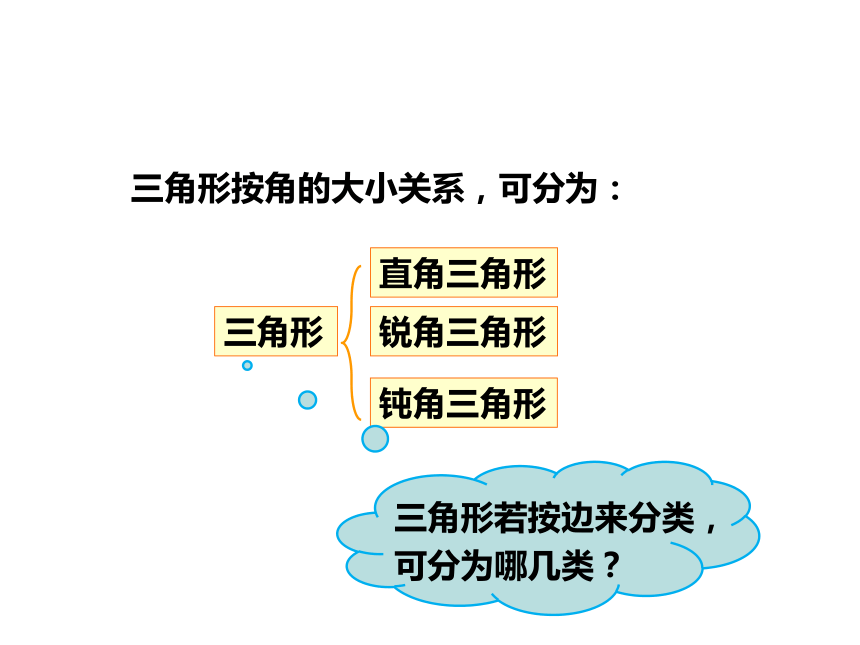
三角形按角的大小关系,可分为:
直角三角形
锐角三角形
钝角三角形
三角形
三角形若按边来分类,可分为哪几类?
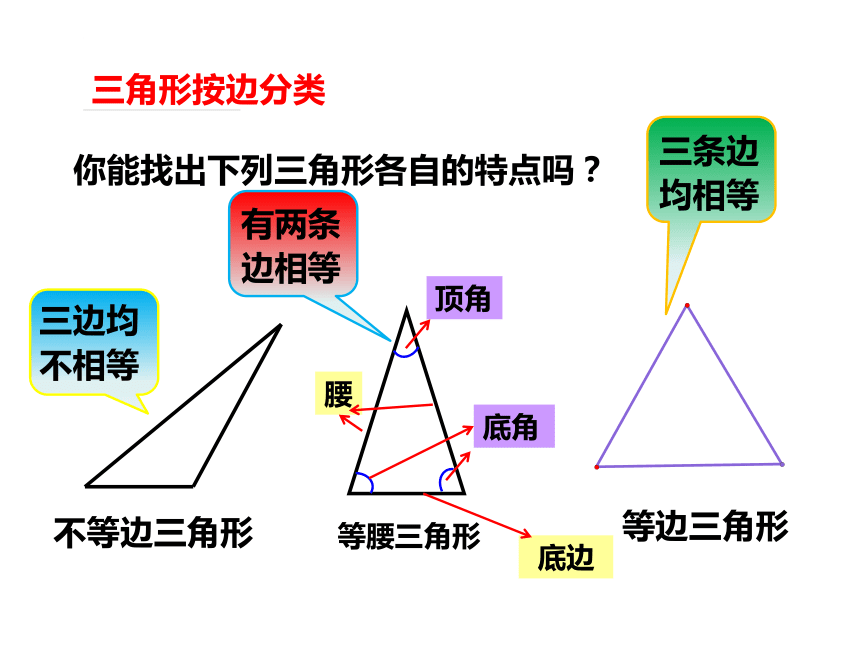
三角形按边分类
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
你能找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
三条边各不相等的三角形叫做不等边三角形 ;
有两条边相等的三角形叫做等腰三角形;
三条边都相等的三角形叫做等边三角形.
等边三角形和等腰三角形之间有什么关系?
总结归纳
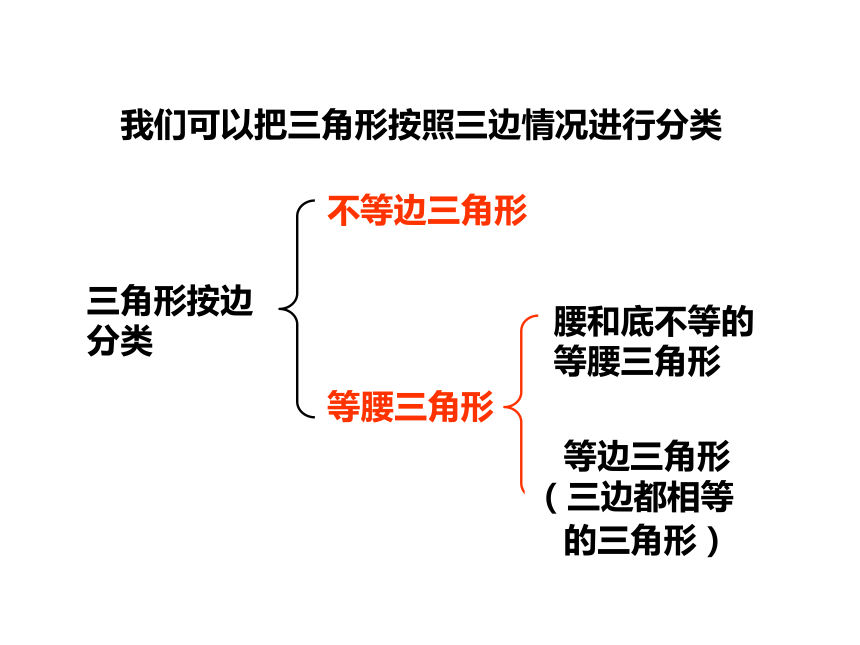
三角形按边分类
不等边三角形
等腰三角形
我们可以把三角形按照三边情况进行分类
腰和底不等的等腰三角形
等边三角形(三边都相等
的三角形)
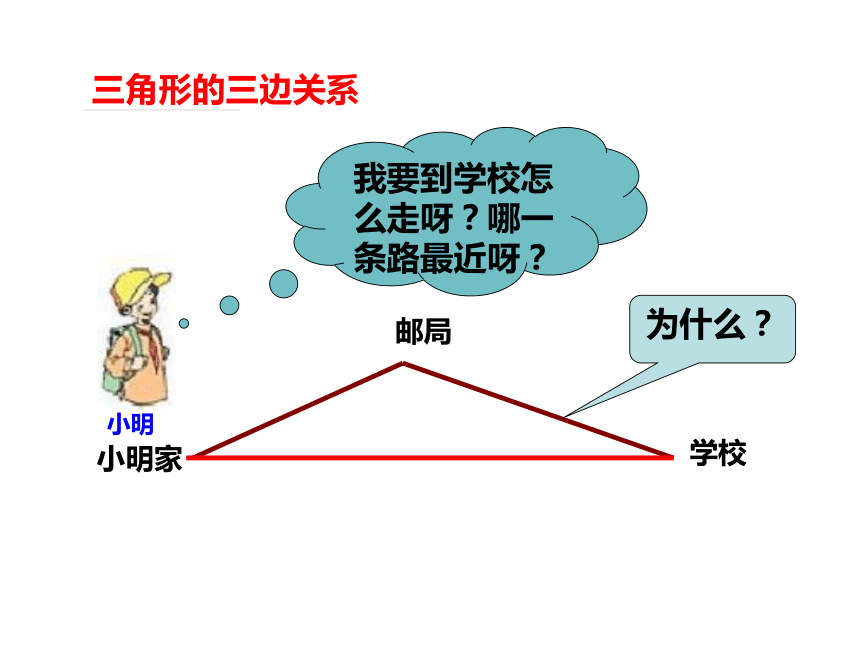
三角形的三边关系
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
小明家
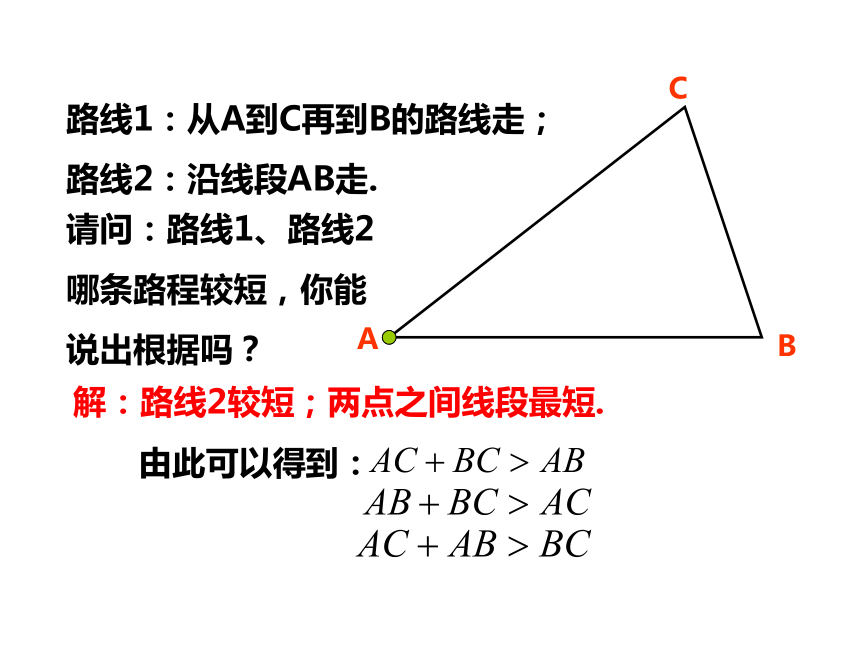
A
B
C
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
归纳总结
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
议一议
1.在同一个三角形中,任意两边之和与第三边有什么
大小关系?
2.在同一个三角形中,任意两边之差与第三边有什么
大小关系?
3.三角形三边有怎样的不等关系?
通过动手实验同学们可以得到哪些结论?理由是什么?
例1 有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
归纳
典例精析
例2 一个三角形的三边长分别为4,7,x,那么
x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
判断三角形边的取值范围要同时运用两边
之和大于第三边,两边之差小于第三边.
归纳
解析:∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11.
A
例3 若a,b,c是△ABC的三边长,化简:|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和
大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
根据两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负.
注意
(2)等边三角形是特殊的等腰三角形;( )
(1)一个钝角三角形一定不是等腰三角形;( )
(3)等腰三角形的腰和底一定不相等;( )
(5)直角三角形一定不是等腰三角形.( )
1.判断:
√
×
×
(4)等边三角形是锐角三角形;( )
×
√
当堂跟踪练习
4.如果等腰三角形的一边长是4cm,另一边长是9cm,
则这个等腰三角形的周长为________.
3.如果等腰三角形的一边长是5cm,另一边长是8cm,
则这个等腰三角形的周长为______________.
2.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其
中三条线段为边长可以构成____个三角形.
3
22cm
18cm或21cm
5.判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;
(3)5cm、6cm、10cm.
判断三条线段是否可以组成三角形,只需说明两条较短线段之和大于第三条线段即可.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
归纳
6.小颖要制作一个三角形木架,现有两根长度为
8cm和5cm的木棒,如果要求第三根木棒的长
度是偶数,小颖有几种选法?第三根的长度可
以是多少?
∵x为偶数,∴小颖有5种选法.
第三根木棒的长度可以是4cm,6cm,8cm,10cm,12cm.
解:设第三根木棒长为xcm,有8-5<x<8+5,
即3<x<13.
7.已知等腰三角形的周长为18cm,如果一边长
等于4cm,求另两边的长?
解:若底边长为4cm,设腰长为x cm,
则2x+4=18,解得x=7.
若一条腰长为4cm,设底边长为x cm,
则2×4+x=18,解得x=10.
因为4+4<10,所以4cm为腰不能构成三角形.
所以三角形另外两个边长都是7cm.
三角形中边的关系
课堂小结
三角形按边分类
不等边三角形
等腰三角形(包括等边三角形)
三角形的三边关系
任意两边之和大于第三边
任意两边之差小于第三边
1.三角形按边分类:
有两边相等的三角形叫做等腰三角形,三边都相等的三角形是等边三角形,
三边互不相等的三角形是不等边三角形.
2.三角形中三边之间的关系:
三角形任意两边之和大于第三边,三角形任意两边之差小于第三边.
板书设计
本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能?为什么不能?初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”.通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既增加了学习兴趣,又增强了学生的动手能力
教学反思
第2课时 三角形的三边关系
第四章 三角形
学习目标
1.掌握三角形按边分类方法,能够判定三角形
是否为特殊的三角形;
2.探索并掌握三角形三边之间的关系,能够运用三角形的
三边关系解决问题.(难点)
数学来源于生活,生活中处处有数学.观察下面的图片,你发现了什么?
问:你能不能给三角形下一个完整的定义?
情境导入
三角形按角的大小关系,可分为:
直角三角形
锐角三角形
钝角三角形
三角形
三角形若按边来分类,可分为哪几类?
三角形按边分类
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
你能找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
三条边各不相等的三角形叫做不等边三角形 ;
有两条边相等的三角形叫做等腰三角形;
三条边都相等的三角形叫做等边三角形.
等边三角形和等腰三角形之间有什么关系?
总结归纳
三角形按边分类
不等边三角形
等腰三角形
我们可以把三角形按照三边情况进行分类
腰和底不等的等腰三角形
等边三角形(三边都相等
的三角形)
三角形的三边关系
小明
我要到学校怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
小明家
A
B
C
路线1:从A到C再到B的路线走;
路线2:沿线段AB走.
请问:路线1、路线2哪条路程较短,你能说出根据吗?
解:路线2较短;两点之间线段最短.
由此可以得到:
归纳总结
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
议一议
1.在同一个三角形中,任意两边之和与第三边有什么
大小关系?
2.在同一个三角形中,任意两边之差与第三边有什么
大小关系?
3.三角形三边有怎样的不等关系?
通过动手实验同学们可以得到哪些结论?理由是什么?
例1 有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
归纳
典例精析
例2 一个三角形的三边长分别为4,7,x,那么
x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
判断三角形边的取值范围要同时运用两边
之和大于第三边,两边之差小于第三边.
归纳
解析:∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11.
A
例3 若a,b,c是△ABC的三边长,化简:|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和
大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
根据两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负.
注意
(2)等边三角形是特殊的等腰三角形;( )
(1)一个钝角三角形一定不是等腰三角形;( )
(3)等腰三角形的腰和底一定不相等;( )
(5)直角三角形一定不是等腰三角形.( )
1.判断:
√
×
×
(4)等边三角形是锐角三角形;( )
×
√
当堂跟踪练习
4.如果等腰三角形的一边长是4cm,另一边长是9cm,
则这个等腰三角形的周长为________.
3.如果等腰三角形的一边长是5cm,另一边长是8cm,
则这个等腰三角形的周长为______________.
2.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其
中三条线段为边长可以构成____个三角形.
3
22cm
18cm或21cm
5.判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;
(3)5cm、6cm、10cm.
判断三条线段是否可以组成三角形,只需说明两条较短线段之和大于第三条线段即可.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
归纳
6.小颖要制作一个三角形木架,现有两根长度为
8cm和5cm的木棒,如果要求第三根木棒的长
度是偶数,小颖有几种选法?第三根的长度可
以是多少?
∵x为偶数,∴小颖有5种选法.
第三根木棒的长度可以是4cm,6cm,8cm,10cm,12cm.
解:设第三根木棒长为xcm,有8-5<x<8+5,
即3<x<13.
7.已知等腰三角形的周长为18cm,如果一边长
等于4cm,求另两边的长?
解:若底边长为4cm,设腰长为x cm,
则2x+4=18,解得x=7.
若一条腰长为4cm,设底边长为x cm,
则2×4+x=18,解得x=10.
因为4+4<10,所以4cm为腰不能构成三角形.
所以三角形另外两个边长都是7cm.
三角形中边的关系
课堂小结
三角形按边分类
不等边三角形
等腰三角形(包括等边三角形)
三角形的三边关系
任意两边之和大于第三边
任意两边之差小于第三边
1.三角形按边分类:
有两边相等的三角形叫做等腰三角形,三边都相等的三角形是等边三角形,
三边互不相等的三角形是不等边三角形.
2.三角形中三边之间的关系:
三角形任意两边之和大于第三边,三角形任意两边之差小于第三边.
板书设计
本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能?为什么不能?初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”.通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既增加了学习兴趣,又增强了学生的动手能力
教学反思
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
