北师大版七年级数学下册 5.1 轴对称现象课件 (共26张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 5.1 轴对称现象课件 (共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 21:15:51 | ||
图片预览






文档简介
5.1 轴对称现象
第五章 生活中的轴对称
学习目标
1.在生活实例中认识轴对称图形;(重点)
2.分析轴对称图形,理解轴对称的概念;(重点)
3.通过丰富的生活实例认识轴对称,能够识别简
单的轴对称图形及其对称轴.(难点)
观察下面的图片:
面对生活中这些美丽的图片,你是否强烈地感受到美就在我们身边!
这是一种怎样的美呢?请谈谈你的感想.
新课情境导入
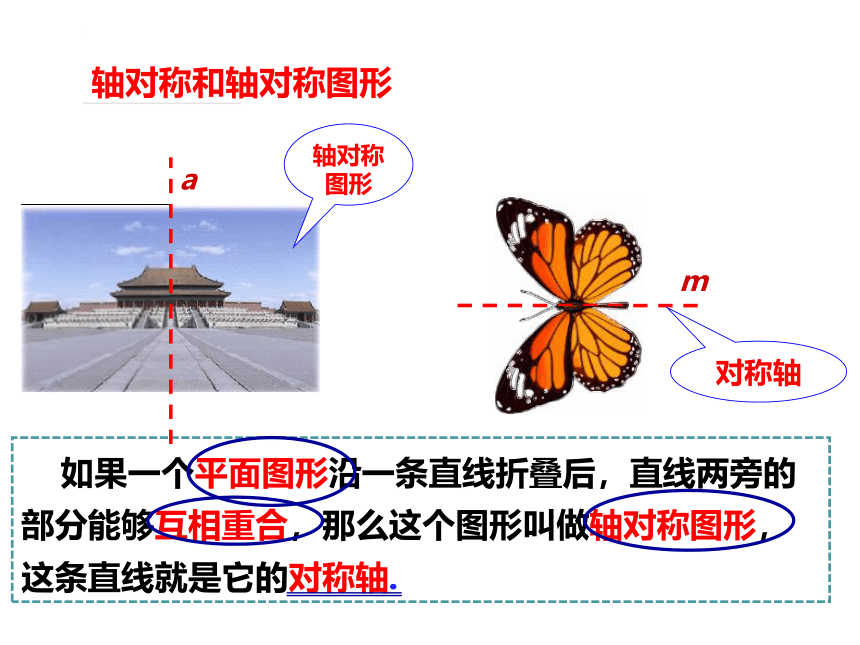
轴对称和轴对称图形
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴.
轴对称图形
对称轴
a
m
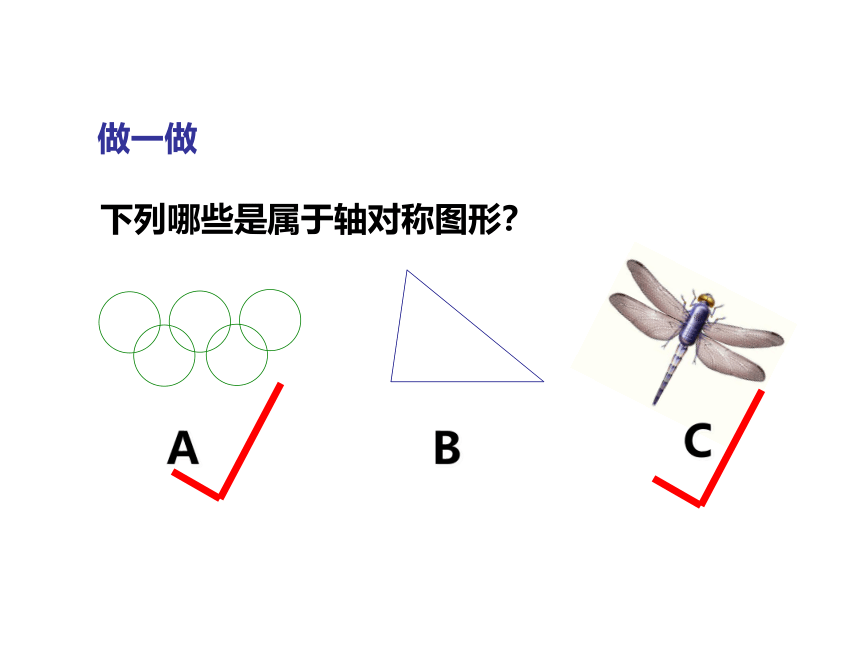
做一做
下列哪些是属于轴对称图形?
A
B
C
你能举出一些轴对称图形的例子吗?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
游戏规则: 每人轮流按顺序报一个字母.如果你认为你所报的字母的形状是一个轴对称图形,你就迅速站起来报出,并说出它有几条对称轴;如果你认为你报的字母的形状不是轴对称图形,那么,你只需坐在座位上报就可以了.其他同学认真听,如果报错了,及时提醒.
全班总动员
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
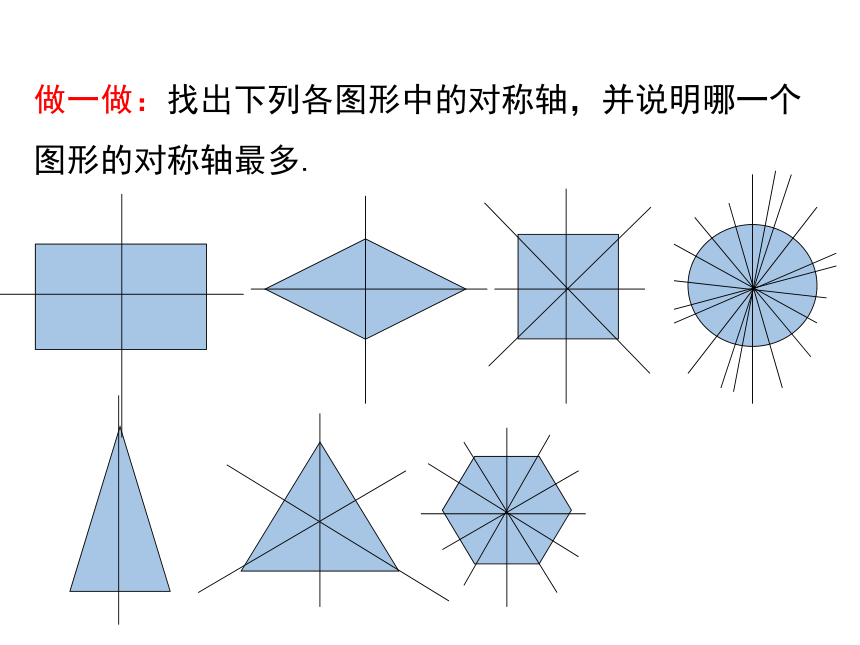
做一做:找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
想一想:下面的每对图形有什么共同特点?
A′
A
B
C
B′
C′
对称轴
对称轴
如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称,这条直线叫做这两个图形的对称轴.
例 下列四组图片中有哪几组图形成轴对称?
B
D
C
A
典例精析
知识要点
比较归纳
轴对称图形
两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
这是轴对称图形还是两个图形成轴对称?
当堂跟踪练习
1.观察下列各种图形,判断是不是轴对称图形?
√
√
√
√
√
√
√
2.找出下面每个轴对称图形的对称轴.
3.找出下文中成轴对称的文字:
一,三,个,八,十,来,苦,天,中.
一叶孤舟,坐着两三个骚客,启用四桨五帆,经过六滩七湾,历尽八颠九簸,可叹十分来迟.十年寒窗,进了九八家书院,抛却七情六欲,苦读五经四书,考了三番两次,今天一定要中.
4.下列英文字母中,哪些是轴对称图形?
A C D E F G H I J L M N O P Q R S T U V W X Y Z
一.中外建筑
二.车标设计
三.国旗欣赏
摩洛哥
瑞典
约旦
英国
肯尼亚
四.交通标志
轴对称现象
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴
课堂小结
如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称
定义
区别
轴对称图形:一个图形具有的特殊形状
轴对称:两个全等图形的特殊的位置关系
1.轴对称图形的定义
2.对称轴
3.两个图形成轴对称
板书设计
这节课充分利用多媒体教学,给学生以直观指导,主动向学生质疑,促使学生思考与发现,形成认识,独立获取知识和技能.另外,借助多媒体教学给学生创设宽松的学习氛围,使学生在学习中始终保持兴奋、愉悦、渴求思索的心理状态,有利于学生主体性的发挥和创新能力的培养
教学反思
第五章 生活中的轴对称
学习目标
1.在生活实例中认识轴对称图形;(重点)
2.分析轴对称图形,理解轴对称的概念;(重点)
3.通过丰富的生活实例认识轴对称,能够识别简
单的轴对称图形及其对称轴.(难点)
观察下面的图片:
面对生活中这些美丽的图片,你是否强烈地感受到美就在我们身边!
这是一种怎样的美呢?请谈谈你的感想.
新课情境导入
轴对称和轴对称图形
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴.
轴对称图形
对称轴
a
m
做一做
下列哪些是属于轴对称图形?
A
B
C
你能举出一些轴对称图形的例子吗?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
游戏规则: 每人轮流按顺序报一个字母.如果你认为你所报的字母的形状是一个轴对称图形,你就迅速站起来报出,并说出它有几条对称轴;如果你认为你报的字母的形状不是轴对称图形,那么,你只需坐在座位上报就可以了.其他同学认真听,如果报错了,及时提醒.
全班总动员
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
做一做:找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
想一想:下面的每对图形有什么共同特点?
A′
A
B
C
B′
C′
对称轴
对称轴
如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称,这条直线叫做这两个图形的对称轴.
例 下列四组图片中有哪几组图形成轴对称?
B
D
C
A
典例精析
知识要点
比较归纳
轴对称图形
两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
这是轴对称图形还是两个图形成轴对称?
当堂跟踪练习
1.观察下列各种图形,判断是不是轴对称图形?
√
√
√
√
√
√
√
2.找出下面每个轴对称图形的对称轴.
3.找出下文中成轴对称的文字:
一,三,个,八,十,来,苦,天,中.
一叶孤舟,坐着两三个骚客,启用四桨五帆,经过六滩七湾,历尽八颠九簸,可叹十分来迟.十年寒窗,进了九八家书院,抛却七情六欲,苦读五经四书,考了三番两次,今天一定要中.
4.下列英文字母中,哪些是轴对称图形?
A C D E F G H I J L M N O P Q R S T U V W X Y Z
一.中外建筑
二.车标设计
三.国旗欣赏
摩洛哥
瑞典
约旦
英国
肯尼亚
四.交通标志
轴对称现象
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴
课堂小结
如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称
定义
区别
轴对称图形:一个图形具有的特殊形状
轴对称:两个全等图形的特殊的位置关系
1.轴对称图形的定义
2.对称轴
3.两个图形成轴对称
板书设计
这节课充分利用多媒体教学,给学生以直观指导,主动向学生质疑,促使学生思考与发现,形成认识,独立获取知识和技能.另外,借助多媒体教学给学生创设宽松的学习氛围,使学生在学习中始终保持兴奋、愉悦、渴求思索的心理状态,有利于学生主体性的发挥和创新能力的培养
教学反思
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
