北师大版七年级数学下册课件:第四章4 .3.1探索三角形全等的条件(共16张))
文档属性
| 名称 | 北师大版七年级数学下册课件:第四章4 .3.1探索三角形全等的条件(共16张)) |  | |
| 格式 | pptx | ||
| 文件大小 | 280.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 22:24:09 | ||
图片预览





文档简介
北师大版七年级下第四章4.3.1
探索三角形全等的条件
一、学习目标
1.经历探索三角形全等的“边边边”的条件的过程.
2.了解三角形的稳定性.
3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
二、温故知新
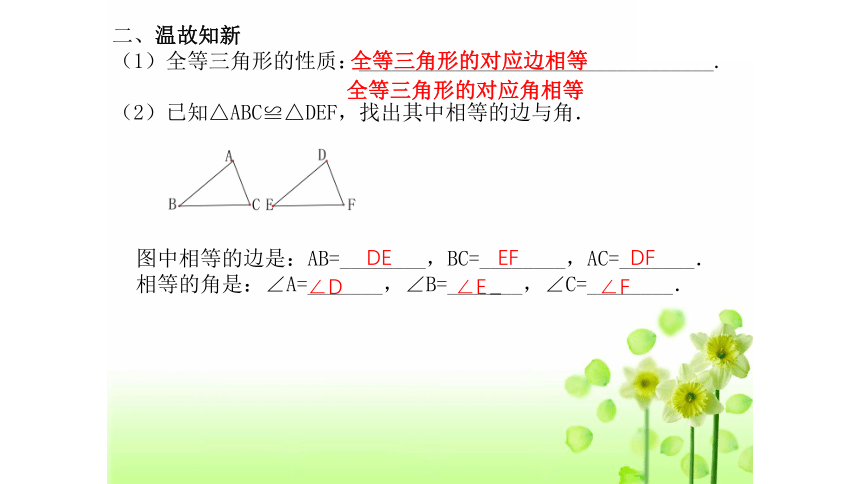
(1)全等三角形的性质:_________________________________.
(2)已知△ABC≌△DEF,找出其中相等的边与角.
图中相等的边是:AB=________,BC=________,AC=_______.
相等的角是:∠A=_______,∠B=____ __,∠C=________.
全等三角形的对应边相等
全等三角形的对应角相等
DE EF DF
∠D ∠E ∠F
三、自主探究:阅读课本p97-99
(1)提出问题:你能画一个三角形与已知的一个三角形全等吗,讨论下面几种情况:
1.给一个条件:只给定一条边时:
只给定一个角时:
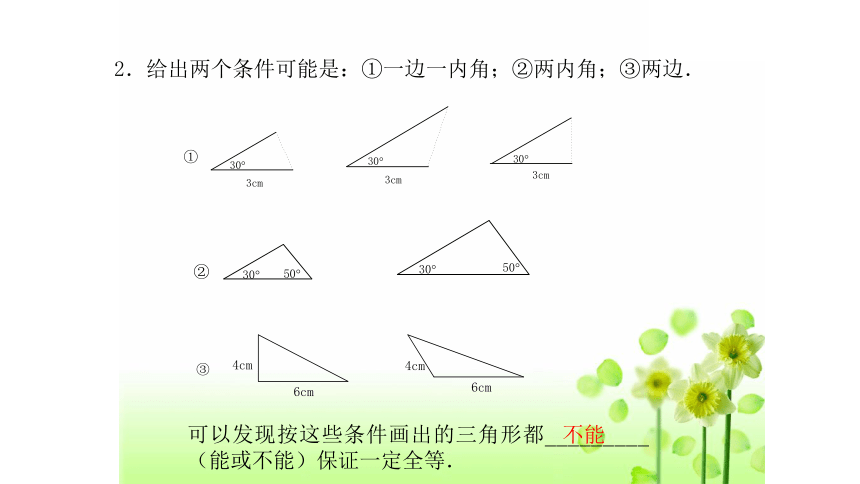
2.给出两个条件可能是:①一边一内角;②两内角;③两边.
可以发现按这些条件画出的三角形都_________(能或不能)保证一定全等.
不能
3.给出三个条件画三角形,你能说出有几种可能的情况吗?
归纳:有四种可能.即:三内角、三条___、两边一内角、两_____一边.
在刚才的探索过程中,我们已经发现三内角不能保证三角形全等.
下面我们就来逐一探索其余的三种情况.
已知一个三角形的三条边长分别为6cm、8cm、10cm.你能画出这个三角形吗?
注:作图方法:先画一线段AB,使得AB=6cm,再分别以A、B为圆心,8cm、10cm为半径画弧,两弧交点记作C,连结线段AC、BC,就可以得到三角形ABC,使得它们的边长分别为AB=6cm,AC=8cm,BC=10cm
.
把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
边
角
通过以上操作可以得出结论:
分别相等的两个三角形全等。简写为______或_________.
4.用三根木条钉成三角形框架,它的大小和形状是固定不变的,而用四根木条钉成的框架,它的形状是可以改变的.三角形的这个性质叫做三角形的稳定性
三角形为什么具有稳定性?
三边
边边边 SSS
例1. 如图,AB=AC, BD=DC 求证:△ABD≌△ACD
证明:在△ABD和△ACD中
∴ △ABD △ACD( )
BD CD
≌
SSS
例2.如图,AM=AN, BM=BN ,求证:△AMB≌△ANB
证明:在△AMB和△ANB中
∴ ≌ ( )
AN 已知
BM
AB AB
△ABM △ABN
SSS
例3、如图,AD=CB,AB=CD ,求证:∠B=∠D
证明:在△ABC和△CDA中
CB=AD
AB=CD
AC=CA
∴ △ABC≌ △CDA(SSS)
例4、如图,PA=PB,PC是△PAB的中线,∠A=55°求∠B的度数
解: ∵ PC是△PAB的中线
∴AC=BC
在△APC和△BPC中
PA=PB
AC=BC
PC=PC
∴ △APC≌△BPC(SSS)
∴ ∠B= ∠A=55°
四、随堂练习
1.两个锐角分别相等的两个直角三角形全等吗?为什么?
两个锐角分别相等的两个直角三角形不一定全等,
因为三个角相等不能证明三角形全等
2.如图,仪器ABCD可以用来平分一个角,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们落在角的两边上,沿AC画一条射线AE,AE就是∠PRQ的平分线,你能说明其中的道理吗?
解:在△ABC和△ADC中
AB=AD
BC=DC
AC=AC
∴△ABC≌△ADE
∴∠BAC=∠DAC
∴AE是∠PRQ的平分线
五、小结:
你还有哪些收获:
哪些疑问:
三边分别相等的两个三角形全等
六.当堂检测:
1、已知:AD=BC,AE=CF,BE=FD,求证:∠B=∠D
证明:∵AE=CF,
∴AE+EF=CF+EF,即AF=CE
在△ADF和△CBE中
AD=BC
BE=FD
AF=CE
∴△ADF≌△CBE
∴∠B=∠D
探索三角形全等的条件
一、学习目标
1.经历探索三角形全等的“边边边”的条件的过程.
2.了解三角形的稳定性.
3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
二、温故知新
(1)全等三角形的性质:_________________________________.
(2)已知△ABC≌△DEF,找出其中相等的边与角.
图中相等的边是:AB=________,BC=________,AC=_______.
相等的角是:∠A=_______,∠B=____ __,∠C=________.
全等三角形的对应边相等
全等三角形的对应角相等
DE EF DF
∠D ∠E ∠F
三、自主探究:阅读课本p97-99
(1)提出问题:你能画一个三角形与已知的一个三角形全等吗,讨论下面几种情况:
1.给一个条件:只给定一条边时:
只给定一个角时:
2.给出两个条件可能是:①一边一内角;②两内角;③两边.
可以发现按这些条件画出的三角形都_________(能或不能)保证一定全等.
不能
3.给出三个条件画三角形,你能说出有几种可能的情况吗?
归纳:有四种可能.即:三内角、三条___、两边一内角、两_____一边.
在刚才的探索过程中,我们已经发现三内角不能保证三角形全等.
下面我们就来逐一探索其余的三种情况.
已知一个三角形的三条边长分别为6cm、8cm、10cm.你能画出这个三角形吗?
注:作图方法:先画一线段AB,使得AB=6cm,再分别以A、B为圆心,8cm、10cm为半径画弧,两弧交点记作C,连结线段AC、BC,就可以得到三角形ABC,使得它们的边长分别为AB=6cm,AC=8cm,BC=10cm
.
把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
边
角
通过以上操作可以得出结论:
分别相等的两个三角形全等。简写为______或_________.
4.用三根木条钉成三角形框架,它的大小和形状是固定不变的,而用四根木条钉成的框架,它的形状是可以改变的.三角形的这个性质叫做三角形的稳定性
三角形为什么具有稳定性?
三边
边边边 SSS
例1. 如图,AB=AC, BD=DC 求证:△ABD≌△ACD
证明:在△ABD和△ACD中
∴ △ABD △ACD( )
BD CD
≌
SSS
例2.如图,AM=AN, BM=BN ,求证:△AMB≌△ANB
证明:在△AMB和△ANB中
∴ ≌ ( )
AN 已知
BM
AB AB
△ABM △ABN
SSS
例3、如图,AD=CB,AB=CD ,求证:∠B=∠D
证明:在△ABC和△CDA中
CB=AD
AB=CD
AC=CA
∴ △ABC≌ △CDA(SSS)
例4、如图,PA=PB,PC是△PAB的中线,∠A=55°求∠B的度数
解: ∵ PC是△PAB的中线
∴AC=BC
在△APC和△BPC中
PA=PB
AC=BC
PC=PC
∴ △APC≌△BPC(SSS)
∴ ∠B= ∠A=55°
四、随堂练习
1.两个锐角分别相等的两个直角三角形全等吗?为什么?
两个锐角分别相等的两个直角三角形不一定全等,
因为三个角相等不能证明三角形全等
2.如图,仪器ABCD可以用来平分一个角,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们落在角的两边上,沿AC画一条射线AE,AE就是∠PRQ的平分线,你能说明其中的道理吗?
解:在△ABC和△ADC中
AB=AD
BC=DC
AC=AC
∴△ABC≌△ADE
∴∠BAC=∠DAC
∴AE是∠PRQ的平分线
五、小结:
你还有哪些收获:
哪些疑问:
三边分别相等的两个三角形全等
六.当堂检测:
1、已知:AD=BC,AE=CF,BE=FD,求证:∠B=∠D
证明:∵AE=CF,
∴AE+EF=CF+EF,即AF=CE
在△ADF和△CBE中
AD=BC
BE=FD
AF=CE
∴△ADF≌△CBE
∴∠B=∠D
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
