北师大版七年级下册数学 1.7 整式的除法(共17张ppt)
文档属性
| 名称 | 北师大版七年级下册数学 1.7 整式的除法(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 425.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览





文档简介
标题
标题
1.7 整式的除法
(2)
= ;
(a ≠ 0,m,n为正整数,m>n)
1.用字母表示幂的运算性质:
n
m
a
(5)
= ;
(4)
= ;
(3)
= ;
.
(6)
=
________ .
.
(1)
= ;
1
(p为正整数)
复习回顾
回顾与思考
2、计算:
(1) a20÷a10 (2) a2n÷an
(3) (?c)4 ÷(?c)2
(4) (a2)3 ·(-a3 )÷(a3)2 ; (5) (x4)6 ÷(x6)2 ·(-x4 )2 。
= a10
= an
= c2
=?a9 ÷a6
=?a3
=x24÷x12 ·x8
=x 24 —12+8
=x20.
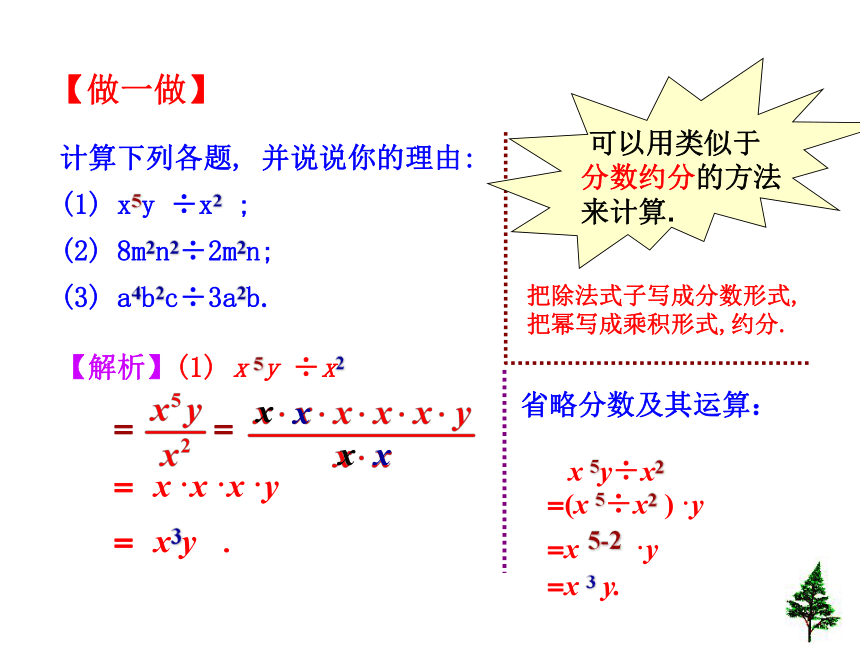
计算下列各题, 并说说你的理由:
(1) x5y ÷x2 ;
(2) 8m2n2÷2m2n;
(3) a4b2c÷3a2b.
【解析】(1) x 5y ÷x2
把除法式子写成分数形式,把幂写成乘积形式,约分.
=
=
= x·x·x·y
x
x
x
x
= x3y .
可以用类似于
分数约分的方法
来计算.
省略分数及其运算:
x 5y÷x2
=(x 5÷x2 )·y
=x 5-2 ·y
=x 3 y.
【做一做】
独立完成(2)(3)小题,
【解析】(2) 8m2n2 ÷2m2n
=(8÷2 )·m2-2·n2-1
=(8÷2 )·(m2÷m2 )·(n2÷n )
=4n.
(3) a4b2c÷3a2b
=(1÷3)(a4÷a2)(b2÷b)c
=(1÷3)a4-2b2-1 c
= a2bc.
被除式的指数 —除式的指数
被除式的系数÷ 除式的系数
商式的系数=
单项式除以单项式,其结果(商式)仍是
(同底数幂) 商的指数=
一个单项式;
指数不变写在商里面作
被除式里单独有的幂,
因式.
x5y ÷ x2 = x5-2·y
8m2n2 ÷ 2m2n = (8÷2 )·m2-1·n2-1 ;
a4b2c ÷ 3a2b = (1÷3 )·a4-2·b2-1·c .
商式
被除式
除式
仔细观察一下,并分析与思考下列几点:
观察 & 归纳
?
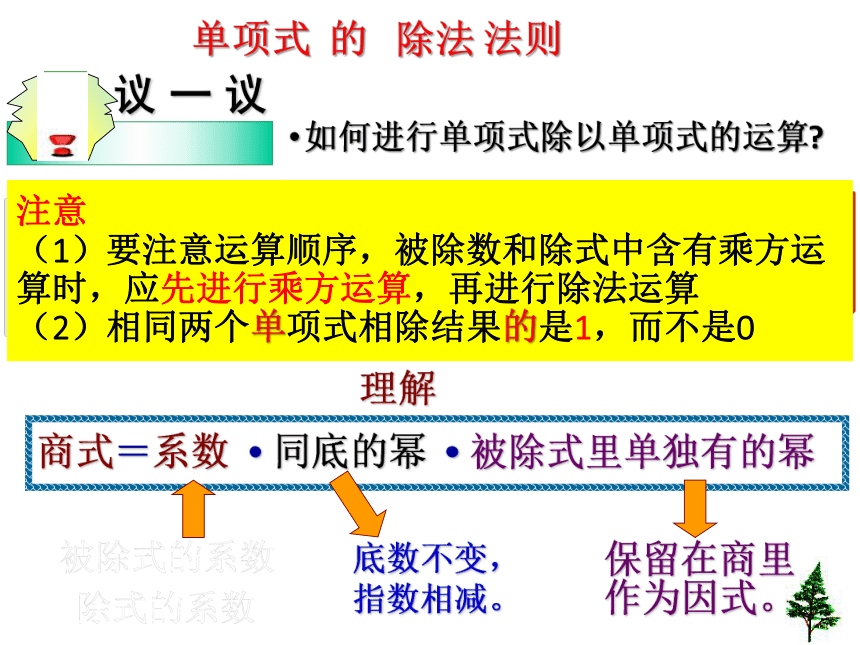
单项式 的 除法 法则
如何进行单项式除以单项式的运算?
议 一 议
单项式相除, 把系数、同底数的幂分别相除后,作为
商的因式;对于只在被除式里含有的字母,则连它的
指数一起作为商的一个因式。
理解
商式=系数 ? 同底的幂 ? 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
注意
(1)要注意运算顺序,被除数和除式中含有乘方运算时,应先进行乘方运算,再进行除法运算
(2)相同两个单项式相除结果的是1,而不是0
例1. 计算:
(1) 28x4y2÷7x3y ; (2) -5a5b3c ÷ 15 a4b
解: (1) 28x4y2÷7x3y
= (28÷7)·x 4-3 y 2-1
= 4xy.
(2) -5a5b3c ÷ 15 a4b
= [ (-5) ÷(15) ] a 5-4 b 3-1 c
= ab2c.
新知识运用
练习 1.计算:
(1)10ab3÷(- 5ab ) ; (2) –8a2b3÷ 6ab2;
(3) -21 x2y4 ÷ (- 3x2 y3) ; (4) (6×10 8) ÷ (3×10 5)
2.把图中左边括号里的每一个式子分别除以2x2y,然后把商式写在右边括号里.
4x3y
-12x4y3
-16x2yz
x2y
÷2x2y
2x
-6x2y2
-8z
二、单项式与多项式相乘的法则是什么?
单项式与多项式相乘,就是用 去乘 的每一项,再把所得的积 。
单项式
多项式
相加
也就是 m(a+b+c)= am+bm+cm
反之,(am+bm+cm)÷m
=a+b+c
=am÷m+bm÷m+cm÷m
你能计算下列各题吗?
(1)(ad+bd)÷d=_____
(2)(a2b+3ab)÷a=_____
(3)(xy3-2xy)÷(xy)=_______
a+b
ab+3b
y2-2
你能找出 多项式除以单项式的规律吗?请说出多项式除以单项式的运算法则。
怎样寻找多项式除以单项式的法则?
不妨从最简的多项式除以单项式人手,
提示:
a+b
理由
( ad+bd )÷d = a+b
用逆运算:ad+bd=d?( )
a+b
提取括号内的公因式、约分:
逆用同分母的加法、约分:
(1)(ad+bd)÷d = __________
(2)(a2b+3ab)÷a = _________
(3)(xy3–2xy)÷(xy) = _______
你能计算下列各题?说说你的理由。
怎样寻找多项式除以单项式的法则?
( ad+bd )÷d =
逆用同分母的
加法、约分:
重点推荐的解法
( ad+bd )÷d
=(ad)÷d
+ (bd)÷d。
省略中间过程
=
上述过程简写为:
( ad+bd )÷d
=(ad)÷d + (bd)÷d。
计算下列各题:
(2)(a2b+3ab)÷a = _________
(3)(xy3–2xy)÷(xy) = _______
ab+3b
y2 –2
你找到了 多项式除以单项式的规律 吗?
议一议
( ad+bd )÷d
=(ad)÷d + (bd)÷d。
多项式除以单项式,
先把这个多项式的每一项分别除以单项式,
再把所得的商相加。
多项式除以单项式的法则
注意:
(1)多项式除以单项式就是把它转化为几个单项式除以单项式,然后再求和
(2)在做除法运算时,应注意各项的符号
(3)商的项数应与原多项式的项数相同
例2 计算:
计算填空:
⑴ (60x3y5) ÷(?12xy3) = ;
◣ ◢
综
(2) (8x6y4z) ÷( ) =?4x2y2 ;
合
(3) 若 (ax3my12)÷(3x3y2n)=4x6y8 ,
则 a = , m = ,n = ;
?5x2y2
?2x4y2z
12
3
2
课 堂 练 习
1.系数相除;
2.同底数幂相除;
3.被除式里单独有的幂不变.
先把这个多项式的每一项分别除以单项式,再把所得的商相加.
一、单项式相除
二、多项式除以单项式
通过本课时的学习,需要我们掌握:
标题
1.7 整式的除法
(2)
= ;
(a ≠ 0,m,n为正整数,m>n)
1.用字母表示幂的运算性质:
n
m
a
(5)
= ;
(4)
= ;
(3)
= ;
.
(6)
=
________ .
.
(1)
= ;
1
(p为正整数)
复习回顾
回顾与思考
2、计算:
(1) a20÷a10 (2) a2n÷an
(3) (?c)4 ÷(?c)2
(4) (a2)3 ·(-a3 )÷(a3)2 ; (5) (x4)6 ÷(x6)2 ·(-x4 )2 。
= a10
= an
= c2
=?a9 ÷a6
=?a3
=x24÷x12 ·x8
=x 24 —12+8
=x20.
计算下列各题, 并说说你的理由:
(1) x5y ÷x2 ;
(2) 8m2n2÷2m2n;
(3) a4b2c÷3a2b.
【解析】(1) x 5y ÷x2
把除法式子写成分数形式,把幂写成乘积形式,约分.
=
=
= x·x·x·y
x
x
x
x
= x3y .
可以用类似于
分数约分的方法
来计算.
省略分数及其运算:
x 5y÷x2
=(x 5÷x2 )·y
=x 5-2 ·y
=x 3 y.
【做一做】
独立完成(2)(3)小题,
【解析】(2) 8m2n2 ÷2m2n
=(8÷2 )·m2-2·n2-1
=(8÷2 )·(m2÷m2 )·(n2÷n )
=4n.
(3) a4b2c÷3a2b
=(1÷3)(a4÷a2)(b2÷b)c
=(1÷3)a4-2b2-1 c
= a2bc.
被除式的指数 —除式的指数
被除式的系数÷ 除式的系数
商式的系数=
单项式除以单项式,其结果(商式)仍是
(同底数幂) 商的指数=
一个单项式;
指数不变写在商里面作
被除式里单独有的幂,
因式.
x5y ÷ x2 = x5-2·y
8m2n2 ÷ 2m2n = (8÷2 )·m2-1·n2-1 ;
a4b2c ÷ 3a2b = (1÷3 )·a4-2·b2-1·c .
商式
被除式
除式
仔细观察一下,并分析与思考下列几点:
观察 & 归纳
?
单项式 的 除法 法则
如何进行单项式除以单项式的运算?
议 一 议
单项式相除, 把系数、同底数的幂分别相除后,作为
商的因式;对于只在被除式里含有的字母,则连它的
指数一起作为商的一个因式。
理解
商式=系数 ? 同底的幂 ? 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
注意
(1)要注意运算顺序,被除数和除式中含有乘方运算时,应先进行乘方运算,再进行除法运算
(2)相同两个单项式相除结果的是1,而不是0
例1. 计算:
(1) 28x4y2÷7x3y ; (2) -5a5b3c ÷ 15 a4b
解: (1) 28x4y2÷7x3y
= (28÷7)·x 4-3 y 2-1
= 4xy.
(2) -5a5b3c ÷ 15 a4b
= [ (-5) ÷(15) ] a 5-4 b 3-1 c
= ab2c.
新知识运用
练习 1.计算:
(1)10ab3÷(- 5ab ) ; (2) –8a2b3÷ 6ab2;
(3) -21 x2y4 ÷ (- 3x2 y3) ; (4) (6×10 8) ÷ (3×10 5)
2.把图中左边括号里的每一个式子分别除以2x2y,然后把商式写在右边括号里.
4x3y
-12x4y3
-16x2yz
x2y
÷2x2y
2x
-6x2y2
-8z
二、单项式与多项式相乘的法则是什么?
单项式与多项式相乘,就是用 去乘 的每一项,再把所得的积 。
单项式
多项式
相加
也就是 m(a+b+c)= am+bm+cm
反之,(am+bm+cm)÷m
=a+b+c
=am÷m+bm÷m+cm÷m
你能计算下列各题吗?
(1)(ad+bd)÷d=_____
(2)(a2b+3ab)÷a=_____
(3)(xy3-2xy)÷(xy)=_______
a+b
ab+3b
y2-2
你能找出 多项式除以单项式的规律吗?请说出多项式除以单项式的运算法则。
怎样寻找多项式除以单项式的法则?
不妨从最简的多项式除以单项式人手,
提示:
a+b
理由
( ad+bd )÷d = a+b
用逆运算:ad+bd=d?( )
a+b
提取括号内的公因式、约分:
逆用同分母的加法、约分:
(1)(ad+bd)÷d = __________
(2)(a2b+3ab)÷a = _________
(3)(xy3–2xy)÷(xy) = _______
你能计算下列各题?说说你的理由。
怎样寻找多项式除以单项式的法则?
( ad+bd )÷d =
逆用同分母的
加法、约分:
重点推荐的解法
( ad+bd )÷d
=(ad)÷d
+ (bd)÷d。
省略中间过程
=
上述过程简写为:
( ad+bd )÷d
=(ad)÷d + (bd)÷d。
计算下列各题:
(2)(a2b+3ab)÷a = _________
(3)(xy3–2xy)÷(xy) = _______
ab+3b
y2 –2
你找到了 多项式除以单项式的规律 吗?
议一议
( ad+bd )÷d
=(ad)÷d + (bd)÷d。
多项式除以单项式,
先把这个多项式的每一项分别除以单项式,
再把所得的商相加。
多项式除以单项式的法则
注意:
(1)多项式除以单项式就是把它转化为几个单项式除以单项式,然后再求和
(2)在做除法运算时,应注意各项的符号
(3)商的项数应与原多项式的项数相同
例2 计算:
计算填空:
⑴ (60x3y5) ÷(?12xy3) = ;
◣ ◢
综
(2) (8x6y4z) ÷( ) =?4x2y2 ;
合
(3) 若 (ax3my12)÷(3x3y2n)=4x6y8 ,
则 a = , m = ,n = ;
?5x2y2
?2x4y2z
12
3
2
课 堂 练 习
1.系数相除;
2.同底数幂相除;
3.被除式里单独有的幂不变.
先把这个多项式的每一项分别除以单项式,再把所得的商相加.
一、单项式相除
二、多项式除以单项式
通过本课时的学习,需要我们掌握:
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
