空间直线与直线的位置关系
图片预览


文档简介
(共29张PPT)
2.1.2空间中直线与直线的位置关系
D
A
′
B
′
C
′
B
A
C
D
′
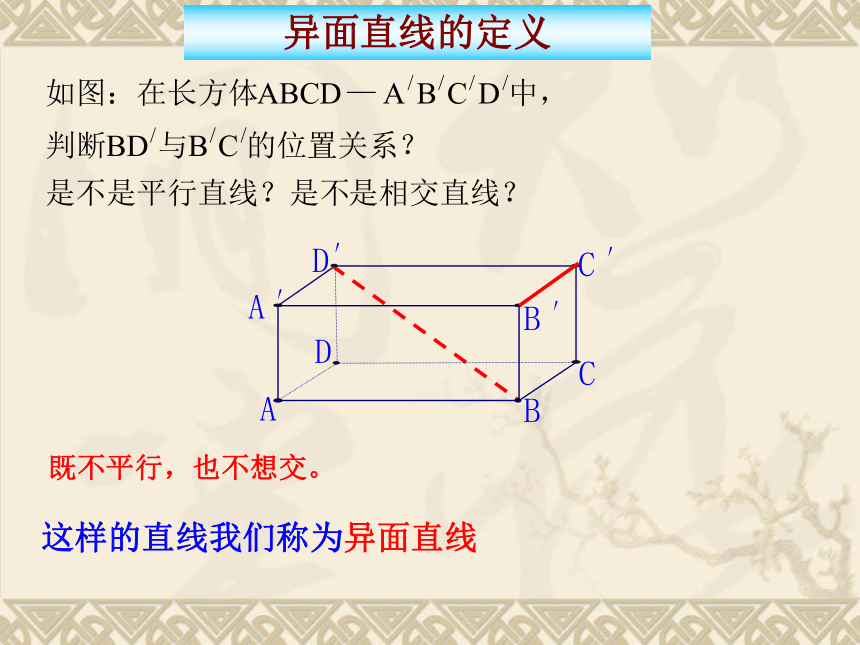
这样的直线我们称为异面直线
既不平行,也不想交。
D
A
′
B
′
C
′
B
A
C
D
′
异面直线的定义
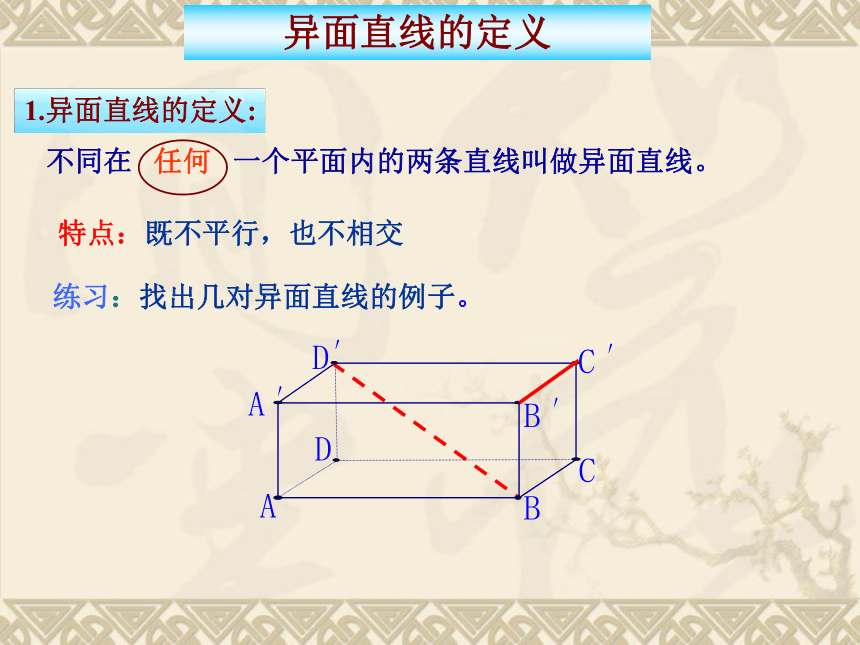
1.异面直线的定义:
不同在 任何 一个平面内的两条直线叫做异面直线。
练习:找出几对异面直线的例子。
异面直线的定义
特点:既不平行,也不相交
D
A
′
B
′
C
′
B
A
C
D
′
异面直线
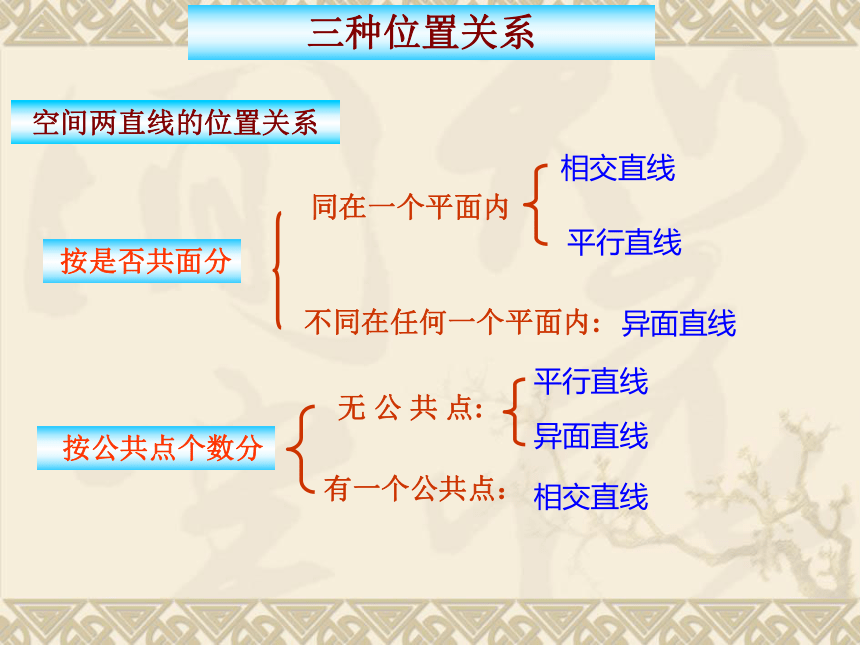
按公共点个数分
有一个公共点:
无 公 共 点:
平行直线
异面直线
相交直线
按是否共面分
同在一个平面内
不同在任何一个平面内:
相交直线
平行直线
空间两直线的位置关系
三种位置关系
问题:在平面几何中,同一个平面内的直线a,b,c,
如果a//b且b//c,那么a//c.这个性质在空间中是否
成立呢?
再探究?
平行公理4
符号表示
公理4实质上是说平行具有传递性,
在平面、空间这个性质都适用.
公理4 平行于同一条直线的两条直线互相平行
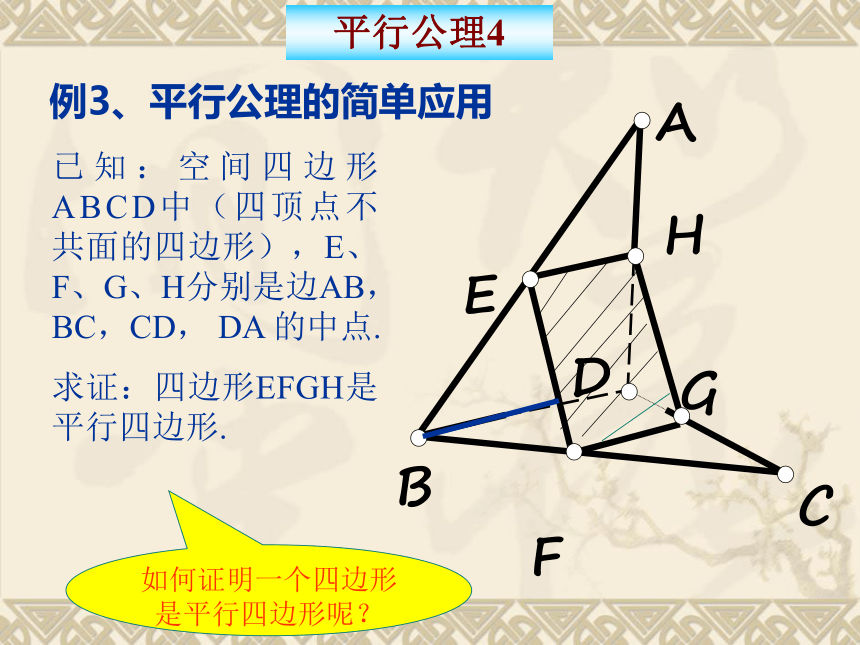
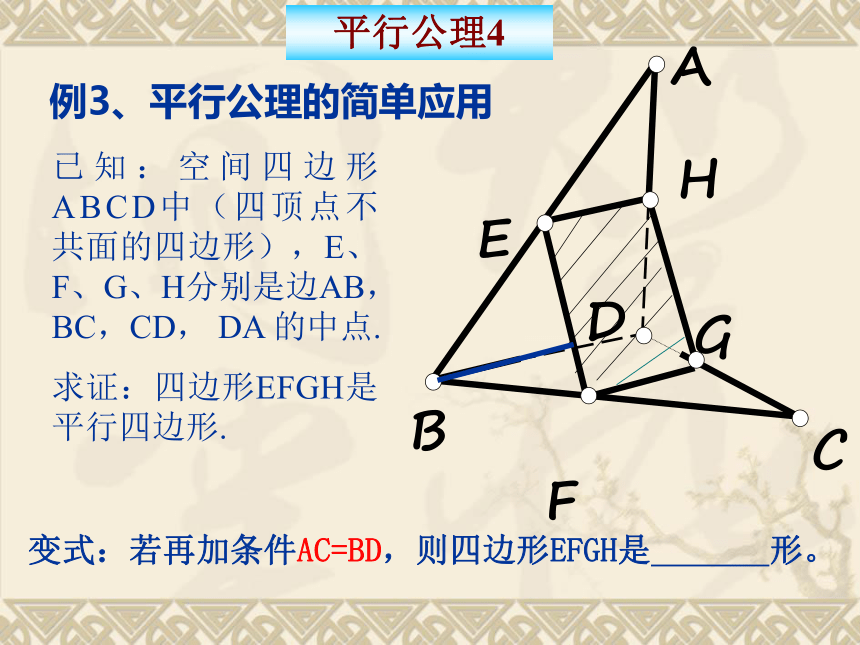
例3、平行公理的简单应用
已知:空间四边形ABCD中(四顶点不共面的四边形),E、F、G、H分别是边AB,BC,CD, DA 的中点.
求证:四边形EFGH是平行四边形.
D
C
B
A
G
F
E
H
如何证明一个四边形是平行四边形呢?
平行公理4
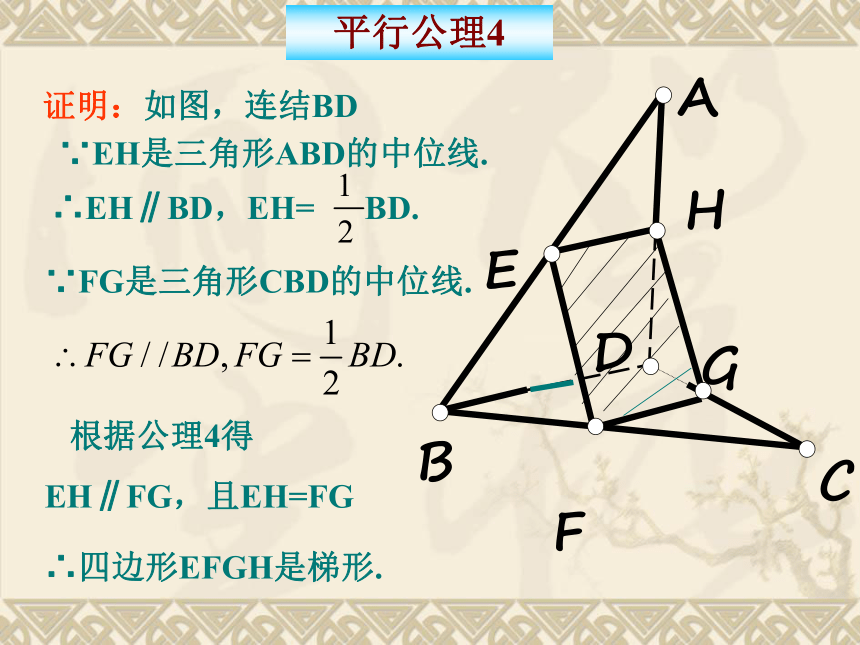
证明:如图,连结BD
∵EH是三角形ABD的中位线.
∴EH∥BD,EH= BD.
根据公理4得
EH∥FG,且EH=FG
∴四边形EFGH是梯形.
∵FG是三角形CBD的中位线.
D
C
B
A
G
F
E
H
平行公理4
例3、平行公理的简单应用
已知:空间四边形ABCD中(四顶点不共面的四边形),E、F、G、H分别是边AB,BC,CD, DA 的中点.
求证:四边形EFGH是平行四边形.
D
C
B
A
G
F
E
H
平行公理4
变式:若再加条件AC=BD,则四边形EFGH是 形。
等角定理
D
A
′
B
′
C
′
B
A
C
D
′
∠1
∠3
∠2
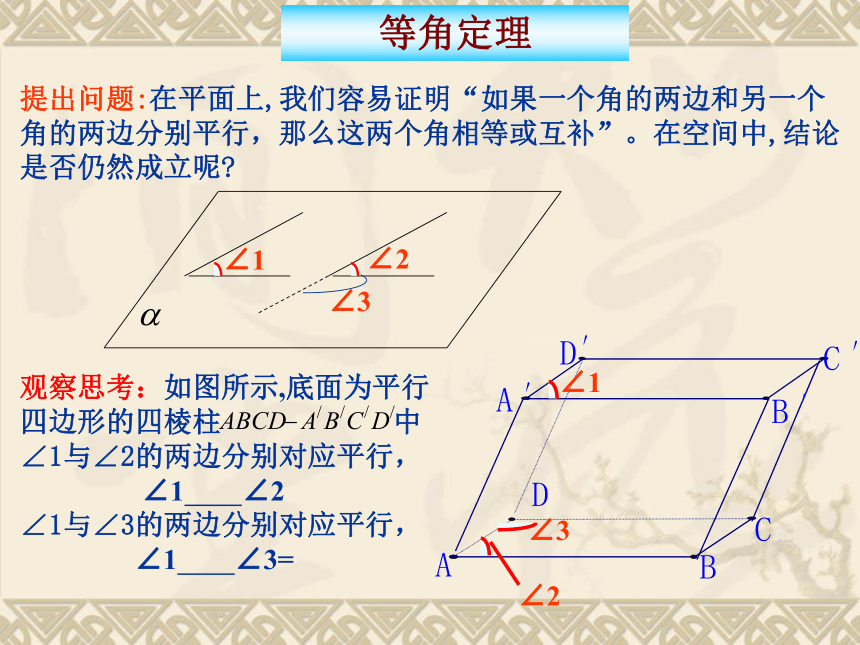
观察思考:如图所示,底面为平行
四边形的四棱柱 中
∠1与∠2的两边分别对应平行,
∠1 ∠2
∠1与∠3的两边分别对应平行,
∠1 ∠3=
提出问题:在平面上,我们容易证明“如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补”。在空间中,结论是否仍然成立呢
∠1
∠2
∠3
定理 如果一个角的两边和另一个角的两边
分别平行并且方向相同,那么这两个角相等
或互补
A1
C1
B1
C
B
A1
B1
C1
A
B
C
D1
等角定理
E1
F1
A
F
E
1.异面直线的定义:
不同在 任何 一个平面内的两条直线叫做异面直线。
异面直线的画法
特点:既不平行,也不相交
说明: 画异面直线时 , 为了体现它们不共面的特点。常借助一个或两个平面来衬托.
如图:
a
a
b
a
A
b
b
(1)
(3)
(2)
2.异面直线的画法:
3.异面直线的判定方法
异面直线判定定理:过平面内一点与平面外一点的直线, 和这个平面内不经过该点的直线是异面直线。
A
B
探究:如图,
异面直线的判定
(1)定义法
(2)既不平行,也不相交
(3)判定定理
C1
D1
A1
B1
A
B
C
D
E
异面直线的判定
初试锋芒:
V
A
B
C
1.如图:在三棱锥V-ABC中,异面直线有
对,分别是 。
终极决战:
2. (1).平面内的一条直线和平面外的一条直线是异面直线;
(2).不同在任一平面内的两条直线是异面直线;
(3).既不相交,又不平行的两条直线是异面直线 .
(4).空间中没有公共点的两条直线是异面直线;
(5).分别在两个不同平面内的两条直线是异面直线;
(6).不同在某一平面内的两条直线是异面直线;
b
b ′
如图,已知两条异面直线 a , b , 经过空间任一点O作 直线 a′∥a , b ′∥b 则把 a ′与 b ′所成的锐角(或直角)叫做异面直线所成的角(或夹角).
a
O
a′
a ″
异面直线所成角的定义:
异面直线所成的角
思考探究:
1.θ的大小和点O的选取是否有关?
一般情况下,点O选在哪里更简单?
2.θ的取值范围是 。
当θ=900 时,我们称这两条异面直线 。
1.已知a,b,c是三条直线,且a//b,a与c的夹角为θ,
那么b与c夹角为 ___________
小试牛刀
θ
×
2. 判断:
③两条直线和第三条直线平行,则这两条直线互相平行.
①两条直线和第三条直线所成的角相等,则这两条直线互相平行.
②两条直线和第三条直线垂直,则这两条直线互相平行.
×
√
异面直线所成的角
(2)哪些棱所在的直线与直线AA1垂直?
解 :直线AB,BC,CD,DA,A1B1,B1C1,C1D1,D1A1分别
与直线AA1垂直.
评析:求异面直线所成的角的步骤是:一找(作)、二说、三求
(1)直线 与 的夹角是多少?
异面直线所成的角
C1
D1
A1
B1
A
B
C
D
E
C1
D1
A1
B1
A
B
C
D
E
达标训练:
答 3对,分别为AB 与CD ;AB与GH; GH与EF
D
C
A
B
G
H
E
F
2、如图,是一个正方体的展开图,如果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有几对?
演示
合作探究:
1、已知长方体ABCD-A1B1C1D1。与AA1平行的棱有 条.
2、已知长方体ABCD-A1B1C1D1 中,
AB=AD=2 ,AA1=2.
(1)BC和A1C1所成的角是多少度?
(2)AA1和BC1所成的角是多少度?
答案:1、3条;2、(1)45度,(2)60度.
A
B
C
D
A1
D1
B1
C1
达标检测
已知:空间四边形ABCD中(四顶点不共面的四边形),E、F、G、H分别是边AB,BC,CD, DA 的中点.
求证:四边形EFGH是平行四边形.
变式一、若加上条件AC=BD,那么四边形EFGH是什么图形?
D
C
B
A
G
F
E
H
变式二、若加上条件AC┴BD,那么四边形EFGH是什么图形?
变式三、若加上条件AC┴BD且AC=BD,且那么四边形EFGH是
什么图形?
思考探究:
1、空间直线的位置关系有几种情景?
平行——判定
相交、 异面——求夹角
2、异面直线定义及平行公理;
3、等角定理;
4、异面直线所成的角.
归纳小结
教材习题2.1A组3、4.
课后作业
2.1.2空间中直线与直线的位置关系
D
A
′
B
′
C
′
B
A
C
D
′
这样的直线我们称为异面直线
既不平行,也不想交。
D
A
′
B
′
C
′
B
A
C
D
′
异面直线的定义
1.异面直线的定义:
不同在 任何 一个平面内的两条直线叫做异面直线。
练习:找出几对异面直线的例子。
异面直线的定义
特点:既不平行,也不相交
D
A
′
B
′
C
′
B
A
C
D
′
异面直线
按公共点个数分
有一个公共点:
无 公 共 点:
平行直线
异面直线
相交直线
按是否共面分
同在一个平面内
不同在任何一个平面内:
相交直线
平行直线
空间两直线的位置关系
三种位置关系
问题:在平面几何中,同一个平面内的直线a,b,c,
如果a//b且b//c,那么a//c.这个性质在空间中是否
成立呢?
再探究?
平行公理4
符号表示
公理4实质上是说平行具有传递性,
在平面、空间这个性质都适用.
公理4 平行于同一条直线的两条直线互相平行
例3、平行公理的简单应用
已知:空间四边形ABCD中(四顶点不共面的四边形),E、F、G、H分别是边AB,BC,CD, DA 的中点.
求证:四边形EFGH是平行四边形.
D
C
B
A
G
F
E
H
如何证明一个四边形是平行四边形呢?
平行公理4
证明:如图,连结BD
∵EH是三角形ABD的中位线.
∴EH∥BD,EH= BD.
根据公理4得
EH∥FG,且EH=FG
∴四边形EFGH是梯形.
∵FG是三角形CBD的中位线.
D
C
B
A
G
F
E
H
平行公理4
例3、平行公理的简单应用
已知:空间四边形ABCD中(四顶点不共面的四边形),E、F、G、H分别是边AB,BC,CD, DA 的中点.
求证:四边形EFGH是平行四边形.
D
C
B
A
G
F
E
H
平行公理4
变式:若再加条件AC=BD,则四边形EFGH是 形。
等角定理
D
A
′
B
′
C
′
B
A
C
D
′
∠1
∠3
∠2
观察思考:如图所示,底面为平行
四边形的四棱柱 中
∠1与∠2的两边分别对应平行,
∠1 ∠2
∠1与∠3的两边分别对应平行,
∠1 ∠3=
提出问题:在平面上,我们容易证明“如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补”。在空间中,结论是否仍然成立呢
∠1
∠2
∠3
定理 如果一个角的两边和另一个角的两边
分别平行并且方向相同,那么这两个角相等
或互补
A1
C1
B1
C
B
A1
B1
C1
A
B
C
D1
等角定理
E1
F1
A
F
E
1.异面直线的定义:
不同在 任何 一个平面内的两条直线叫做异面直线。
异面直线的画法
特点:既不平行,也不相交
说明: 画异面直线时 , 为了体现它们不共面的特点。常借助一个或两个平面来衬托.
如图:
a
a
b
a
A
b
b
(1)
(3)
(2)
2.异面直线的画法:
3.异面直线的判定方法
异面直线判定定理:过平面内一点与平面外一点的直线, 和这个平面内不经过该点的直线是异面直线。
A
B
探究:如图,
异面直线的判定
(1)定义法
(2)既不平行,也不相交
(3)判定定理
C1
D1
A1
B1
A
B
C
D
E
异面直线的判定
初试锋芒:
V
A
B
C
1.如图:在三棱锥V-ABC中,异面直线有
对,分别是 。
终极决战:
2. (1).平面内的一条直线和平面外的一条直线是异面直线;
(2).不同在任一平面内的两条直线是异面直线;
(3).既不相交,又不平行的两条直线是异面直线 .
(4).空间中没有公共点的两条直线是异面直线;
(5).分别在两个不同平面内的两条直线是异面直线;
(6).不同在某一平面内的两条直线是异面直线;
b
b ′
如图,已知两条异面直线 a , b , 经过空间任一点O作 直线 a′∥a , b ′∥b 则把 a ′与 b ′所成的锐角(或直角)叫做异面直线所成的角(或夹角).
a
O
a′
a ″
异面直线所成角的定义:
异面直线所成的角
思考探究:
1.θ的大小和点O的选取是否有关?
一般情况下,点O选在哪里更简单?
2.θ的取值范围是 。
当θ=900 时,我们称这两条异面直线 。
1.已知a,b,c是三条直线,且a//b,a与c的夹角为θ,
那么b与c夹角为 ___________
小试牛刀
θ
×
2. 判断:
③两条直线和第三条直线平行,则这两条直线互相平行.
①两条直线和第三条直线所成的角相等,则这两条直线互相平行.
②两条直线和第三条直线垂直,则这两条直线互相平行.
×
√
异面直线所成的角
(2)哪些棱所在的直线与直线AA1垂直?
解 :直线AB,BC,CD,DA,A1B1,B1C1,C1D1,D1A1分别
与直线AA1垂直.
评析:求异面直线所成的角的步骤是:一找(作)、二说、三求
(1)直线 与 的夹角是多少?
异面直线所成的角
C1
D1
A1
B1
A
B
C
D
E
C1
D1
A1
B1
A
B
C
D
E
达标训练:
答 3对,分别为AB 与CD ;AB与GH; GH与EF
D
C
A
B
G
H
E
F
2、如图,是一个正方体的展开图,如果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有几对?
演示
合作探究:
1、已知长方体ABCD-A1B1C1D1。与AA1平行的棱有 条.
2、已知长方体ABCD-A1B1C1D1 中,
AB=AD=2 ,AA1=2.
(1)BC和A1C1所成的角是多少度?
(2)AA1和BC1所成的角是多少度?
答案:1、3条;2、(1)45度,(2)60度.
A
B
C
D
A1
D1
B1
C1
达标检测
已知:空间四边形ABCD中(四顶点不共面的四边形),E、F、G、H分别是边AB,BC,CD, DA 的中点.
求证:四边形EFGH是平行四边形.
变式一、若加上条件AC=BD,那么四边形EFGH是什么图形?
D
C
B
A
G
F
E
H
变式二、若加上条件AC┴BD,那么四边形EFGH是什么图形?
变式三、若加上条件AC┴BD且AC=BD,且那么四边形EFGH是
什么图形?
思考探究:
1、空间直线的位置关系有几种情景?
平行——判定
相交、 异面——求夹角
2、异面直线定义及平行公理;
3、等角定理;
4、异面直线所成的角.
归纳小结
教材习题2.1A组3、4.
课后作业
