沪教版(上海)初中数学九年级上册 24.4 相似三角形的判定 教案
文档属性
| 名称 | 沪教版(上海)初中数学九年级上册 24.4 相似三角形的判定 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 64.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 16:33:17 | ||
图片预览

文档简介
24.4(5)相似三角形的判定
教学目标
综合运用所学判定定理结合相似三角形的定义进行判定或计算.
教学重点及难点
根据图形特征和已知条件合理选择判定定理进行证明和计算.
教学用具准备
三角板、课件
教学过程
一、复习引入
1、相似三角形的判定方法
相似三角形的
判定方法
条件
结论
(1)定义法(一般不用)
三个角对应相等、三条边对应成比例,
两三角形相似
(2)预备定理
平行于三角形一边的直线截其它两边所在的直线,
截得的三角形与原三角形相似
(3)三角形相似的传递性
两个三角形分别与同一个三角形相似,
这两三角形也相似
(4)相似三角形判定定理1.
两角对应相等,
两三角形相似
(5)相似三角形判定定理2.
两边对应成比例且夹角相等,
两三角形相似
(6)相似三角形判定定理3.
三边对应成比例,
两三角形相似
(7)相似三角形判定定理4.
斜边和一条直角边对应成比例,
两三角形相似
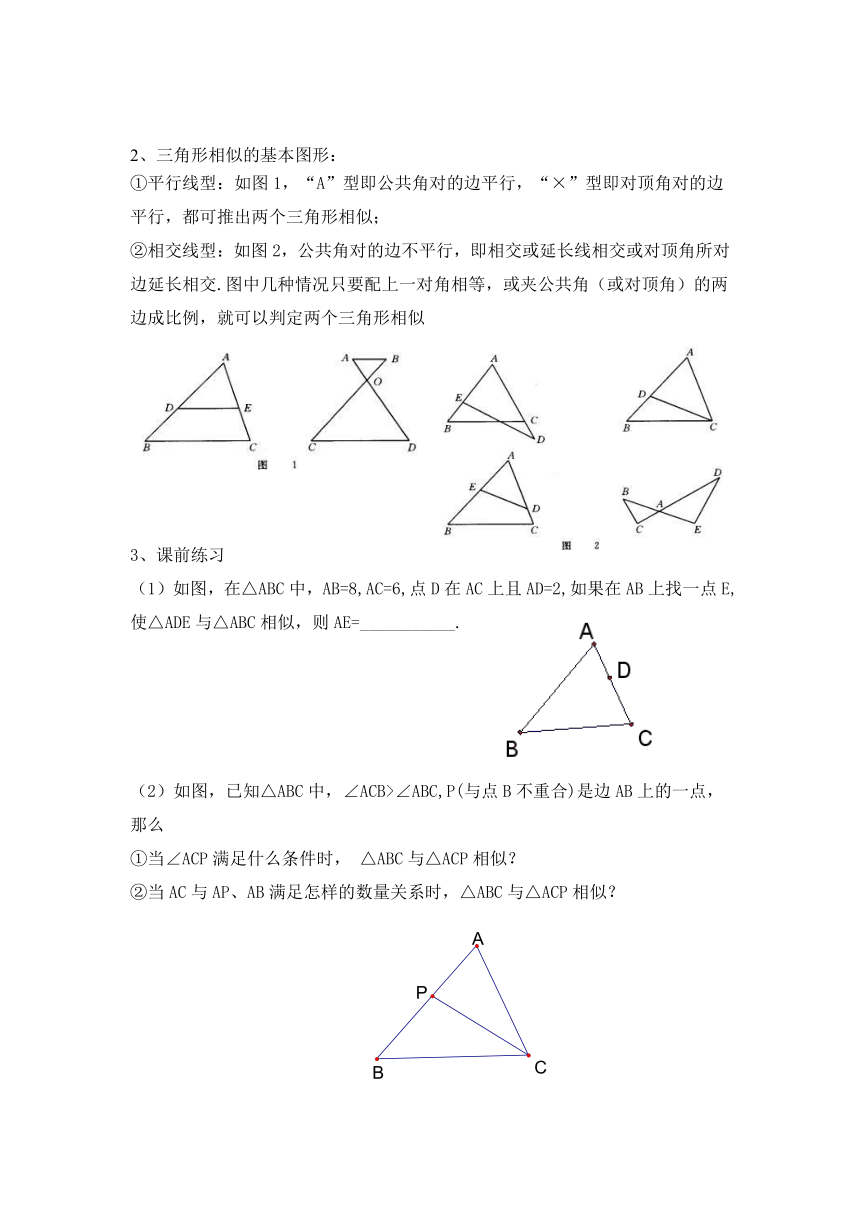
2、三角形相似的基本图形:
①平行线型:如图1,“A”型即公共角对的边平行,“×”型即对顶角对的边平行,都可推出两个三角形相似;
②相交线型:如图2,公共角对的边不平行,即相交或延长线相交或对顶角所对边延长相交.图中几种情况只要配上一对角相等,或夹公共角(或对顶角)的两边成比例,就可以判定两个三角形相似
3、课前练习
(1)如图,在△ABC中,AB=8,AC=6,点D在AC上且AD=2,如果在AB上找一点E,使△ADE与△ABC相似,则AE=___________.
(2)如图,已知△ABC中,∠ACB>∠ABC,P(与点B不重合)是边AB上的一点,那么
①当∠ACP满足什么条件时,
△ABC与△ACP相似?
②当AC与AP、AB满足怎样的数量关系时,△ABC与△ACP相似?
二、例题研究
例题5
已知,在△和△中,,,垂足、分别在边、上,且.求证:∽.
例题6、已知:点分别在射线PM、PN、PT上,AB//,
BC//.求证:
∽.
引导学生结合图形,一题多解
三、练习巩固
练习1:书后练习24.4(5)/2
练习2:如图,在△ABC中,AD、BE分别是BC、AC上的高,AD、BE相交于H,则图中相似的三角形共有(
)对.
A.3
B.4
C.5
D.6
练习3:如图,CD是△ABC中∠ACB的平分线,E是AC上一点,CD2=CB·CE.
求证:(1)△CED∽△CDB
(2)△ADE∽△ACD
练习4:如图,AB⊥BD,CD⊥BD,AP⊥PC,AB=6,CD=16,BD=20,点P在线段BD上,求BP的长。
变式练习:如图,AB⊥BD,CD⊥BD,AB=6,CD=16,BD=20,点P在线段BD上,求当BP的长为多少时,△PAB与△PCD是相似三角形?
改编:如图,AB⊥BD,CD⊥BD,AB=6,CD=16,BD=20,一动点P在线段BD上,从点B开始向点D运动,问当点P离开点B有多远时,求当BP的长为多少时,△PAB与△PCD是相似三角形?试求出所有符合条件的P点的位置。
四、课堂总结
1、观察基本图形
2、掌握基本定理
3、学会合理推理
4、注重数学思想
五、作业布置
练习册24.4(5)
教学目标
综合运用所学判定定理结合相似三角形的定义进行判定或计算.
教学重点及难点
根据图形特征和已知条件合理选择判定定理进行证明和计算.
教学用具准备
三角板、课件
教学过程
一、复习引入
1、相似三角形的判定方法
相似三角形的
判定方法
条件
结论
(1)定义法(一般不用)
三个角对应相等、三条边对应成比例,
两三角形相似
(2)预备定理
平行于三角形一边的直线截其它两边所在的直线,
截得的三角形与原三角形相似
(3)三角形相似的传递性
两个三角形分别与同一个三角形相似,
这两三角形也相似
(4)相似三角形判定定理1.
两角对应相等,
两三角形相似
(5)相似三角形判定定理2.
两边对应成比例且夹角相等,
两三角形相似
(6)相似三角形判定定理3.
三边对应成比例,
两三角形相似
(7)相似三角形判定定理4.
斜边和一条直角边对应成比例,
两三角形相似
2、三角形相似的基本图形:
①平行线型:如图1,“A”型即公共角对的边平行,“×”型即对顶角对的边平行,都可推出两个三角形相似;
②相交线型:如图2,公共角对的边不平行,即相交或延长线相交或对顶角所对边延长相交.图中几种情况只要配上一对角相等,或夹公共角(或对顶角)的两边成比例,就可以判定两个三角形相似
3、课前练习
(1)如图,在△ABC中,AB=8,AC=6,点D在AC上且AD=2,如果在AB上找一点E,使△ADE与△ABC相似,则AE=___________.
(2)如图,已知△ABC中,∠ACB>∠ABC,P(与点B不重合)是边AB上的一点,那么
①当∠ACP满足什么条件时,
△ABC与△ACP相似?
②当AC与AP、AB满足怎样的数量关系时,△ABC与△ACP相似?
二、例题研究
例题5
已知,在△和△中,,,垂足、分别在边、上,且.求证:∽.
例题6、已知:点分别在射线PM、PN、PT上,AB//,
BC//.求证:
∽.
引导学生结合图形,一题多解
三、练习巩固
练习1:书后练习24.4(5)/2
练习2:如图,在△ABC中,AD、BE分别是BC、AC上的高,AD、BE相交于H,则图中相似的三角形共有(
)对.
A.3
B.4
C.5
D.6
练习3:如图,CD是△ABC中∠ACB的平分线,E是AC上一点,CD2=CB·CE.
求证:(1)△CED∽△CDB
(2)△ADE∽△ACD
练习4:如图,AB⊥BD,CD⊥BD,AP⊥PC,AB=6,CD=16,BD=20,点P在线段BD上,求BP的长。
变式练习:如图,AB⊥BD,CD⊥BD,AB=6,CD=16,BD=20,点P在线段BD上,求当BP的长为多少时,△PAB与△PCD是相似三角形?
改编:如图,AB⊥BD,CD⊥BD,AB=6,CD=16,BD=20,一动点P在线段BD上,从点B开始向点D运动,问当点P离开点B有多远时,求当BP的长为多少时,△PAB与△PCD是相似三角形?试求出所有符合条件的P点的位置。
四、课堂总结
1、观察基本图形
2、掌握基本定理
3、学会合理推理
4、注重数学思想
五、作业布置
练习册24.4(5)
