鲁教版数学八年级上4.4频数和频率课件(2课时)
文档属性
| 名称 | 鲁教版数学八年级上4.4频数和频率课件(2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-21 20:30:51 | ||
图片预览









文档简介
(共47张PPT)
*
第一课时
济宁十二中 陈伟利
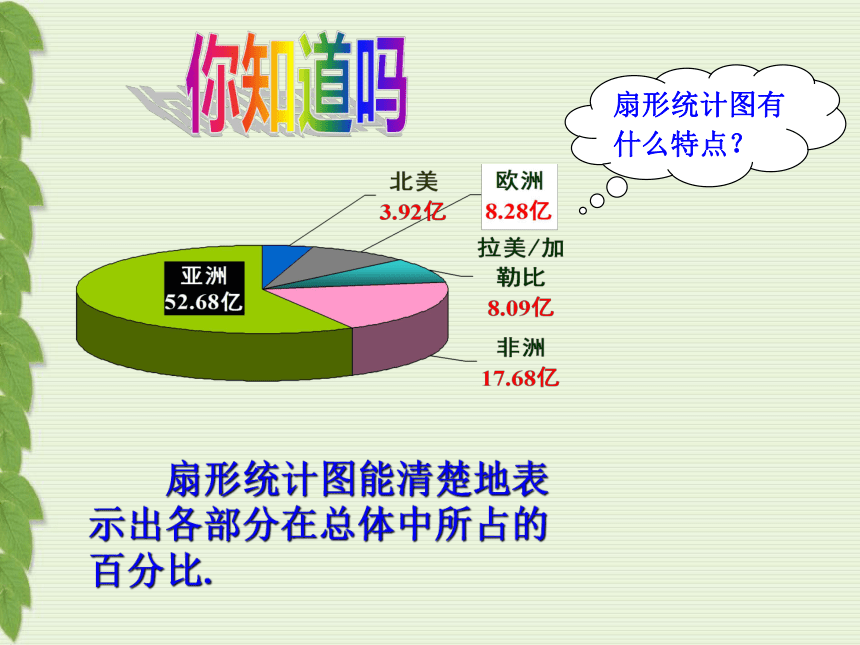
人们常用哪三种统计图表示一组数据?
扇形统计图
条形统计图
折线统计图
扇形统计图能清楚地表示出各部分在总体中所占的百分比.
扇形统计图有什么特点?
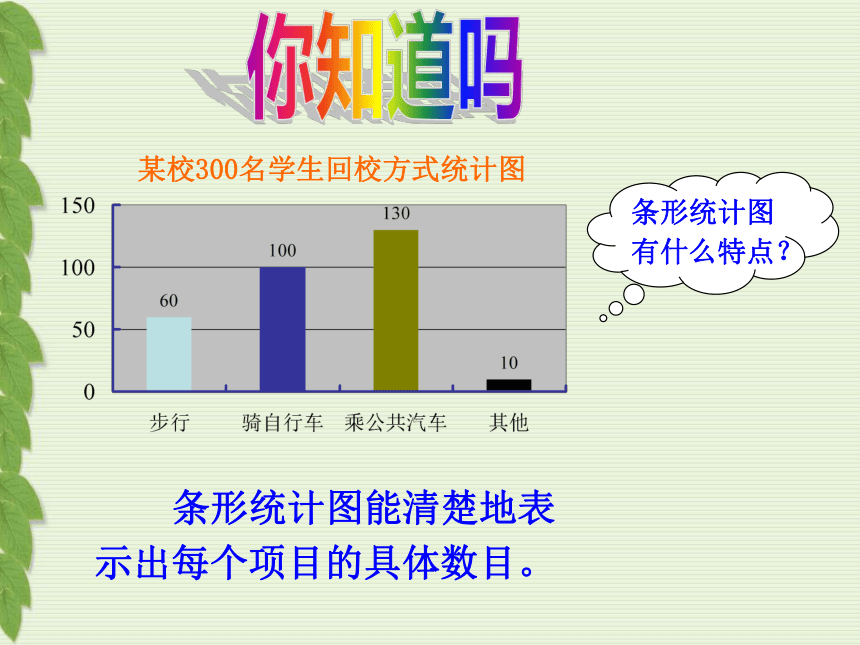
条形统计图能清楚地表示出每个项目的具体数目。
某校300名学生回校方式统计图
条形统计图有什么特点?
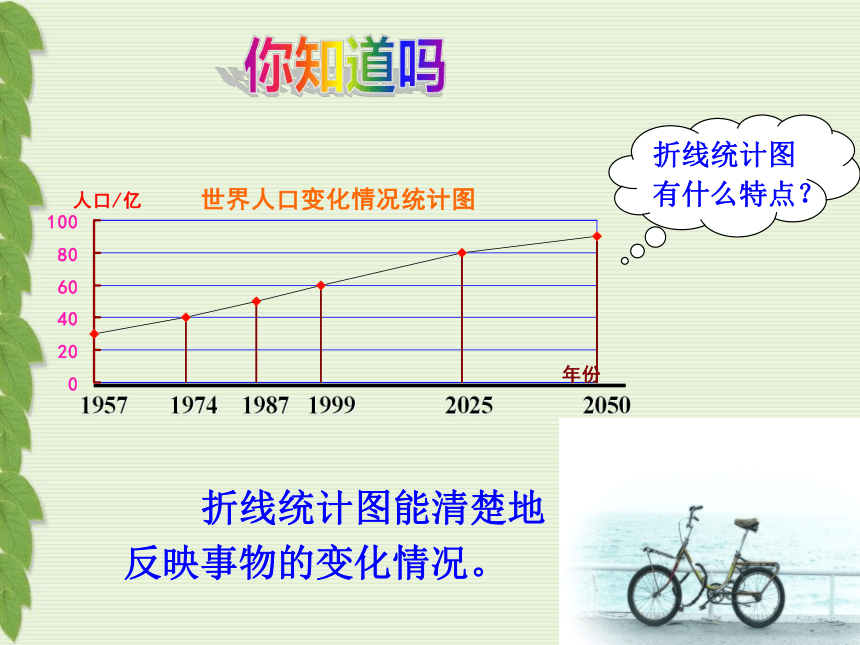
1957 1974 1987 1999 2025 2050
折线统计图有什么特点?
折线统计图能清楚地反映事物的变化情况。
1、某专业户要出售100只羊,现在市场上羊的价格为每千克11元,为了估计这100只羊能卖多少钱,该专业户从中随机抽取5只羊,每只羊的质量如下(单位:千克):26,31,32,36,37.
(1)估计这100只羊每只的平均价格;
(2)估计这100只羊一共能卖多少钱?
巩固习题
解析:(1)先求出5只羊中每只羊的平均质量,从而估计100只羊的平均质量;
(2)先估计100只羊的总质量,再乘一每千克的价格,即为所求。
(1)X=1/5(26+31+32+36+37)=32.4(kg)
所以估计这100只羊的平均质32.4kg。
(2)32.4×100×11=35640(元)
所以估计这100只羊一共能卖35640。
2:李敏的爸爸在山上种了橙果树44株,现进入收获期,收获时,先随意采摘5株果树上的橙子,称得每株果树上橙子的质量如下(单位:kg)
35,35,34,39,37.
(1)在这个问题中,总体、样本各是什么 ?
(2)若市场上橙子售价为每千克5元,则这年李敏家卖橙子收入将达多少元?
巩固习题
(1)44株橙果树的质量是总体
采摘的5株果树上的橙子的质量是总体的一个样本
(2)x=1/5(35+35+34+39+37)
=36(kg)
36×44×5=7920(元)
小结 拓展
C
D
B
A
频数与频率
你喜欢看足球比赛吗?你喜欢的足球明星是谁?
小明调查了八(1)班50名同学最喜欢的足球明星,结果如下: (其中A代表贝克汉母,B代表费戈,C代表罗纳尔多,D代表巴乔).
领悟新知
A A B C D A B A A C
B A A C B C A A B C
A A B A C D A A C D
B A C D A A A C D A
C B A A C C D A A C
有无捷径
一目了然
根据这个结果,你能很快说出该班同学最喜欢的足球明星吗?
领悟新知
你认为小明的数据表示方式好不好?你能设计出一个比较好的表示方式吗?
A A B C D A B A A C
B A A C B C A A B C
A A B A C D A A C D
B A C D A A A C D A
C B A A C C D A A C
象这样的表格称为频数分布表.它可以用唱票的方法来制作.
一表知“情”
小丽根据小明的结果,制成了下面的图表,你能从中迅速判断出该班同学最喜欢的足球明星吗?
关注数据
足球明星 学生数
A 正正正正 23
B 正 8
C 正正 13
D 正一 6
明星
学生人数
A
B
C
25
20
15
10
5
D
象这样的图称为频数分布直方图.
一数知“情”
开启智慧
从上表可以看出,A,B,C,D出现的次数有的多,有的少,或者说它们出现的频繁程度不同.我们称每个对象出现的次数为频数(absolute frequency),而每个对象出现的次数与总次数的比值为频率(relative frequency).
如,A的频数为23.A的频率为23/50或 .
足球明星 学生数
A 正正正正 23
B 正 8
C 正正 13
D 正一 6
频率=
频数
总次数
频数=
频数,频率和总个数之间的公式:
总次数=
频率
频数
频率 X 总次数
练习 :
1.某班60名同学中,身高为1.50米—1.65米的人数为12人,那么这组数据的频数是___,频率是____.
2.某班学生参加考试,分数是60-70分的组的人数20,该组的频率是0.20,则这班有__人.
3.为了了解某单位青年人现在对自己所从事工作的满意程度,小明随机调查了该单位一批青年,数所据如下(1表不满意,2表示不满意,3表示一般,4表示满意,5表示很满意):
2 5 4 5 2 5 3 1 2 3
4 4 3 3 5 2 1 4 3 3
3 4 4 2 5 5 4 4 4 2
3 2 4 3 3 5 1 1 5 3
4 1 2 2 3 4 3 3 1 4
根据上述信息填右表;你认为该单位青年人现在对自己所从事工作的满意吗
调查情况 频数 频率
很不满意
不满意
一般
满意
很满意
合计
练习:为了了解某种小麦麦穗的长度,科技人员抽测实验田麦穗 的长度,列表如下:
(1)表中未完成部分:
a=__,b=__,c=__,d=__,
e=__,f=__,g=____.
(2)该问题的总体是_______;
个体是_____________;
样本是_____________.
(3)所测样本中共有___数据.
长度在5.95—6.45cm的麦穗
占总数的百分之几 ______.
(5)众数在_____组,中位数在_____组.
组数 分组 频数 频率
1 4.45—4.95 a 0.05
2 4.95—5.45 2 e
3 5.45—5.95 6 0.30
4 5.95—6.45 b f
5 6.45—6.95 c 0.25
合计 d g
“频率”知多少
看法相同的同学组成一个小组,设计一个简单的调查方案,粗略地估计一下它的使用频率,并将调查结果在全班交流 .
你认为哪个汉字的使用频率最高?
做一做
一图知“情”
小明和小亮从同一本书中分别随机抽取了6页,在统计了1页,2页,3页,4页,5页,6页“的”和“了”出现的次数后,分别求出了它们出现的频率,并绘制了下图:
议一议P186
随着统计页数的增加,这两个字出现的频率是如何变化的
你认为该书中“的”和“了”两个字的使用频率哪个高
频率
●
1 2 3 4 5 6
统计的页数
0.06
0.05
0.04
0.03
0.02
0.01
图例:
■的
●了
●
●
●
●
●
■
■
■
■
■
■
象这样的图称为频数分布折线图.
一节课下来:
我最大的收获是______________
我对自己的表现感想如何_____________
我对同伴的感想如何________________
我从同学身上学到了________________
你能用本节课的知识设计一个问题,并设法 解决吗
知识的升华
独立
作业
*
第二课时
济宁十二中 陈伟利
频数与频率
回顾与思考
1。在统计里,我们称每个考查对象出现的次数为——,每个对象出现的次数与总次数的比值为——。
频数
频率
2。各对象的频数之和等于————,各频率之和等于————。
数据总和
单位1
3。已知一个样本中,50个数据分别落在5个组内,第一,二,三,五的数据个数分别为 2,8,15,5,则第四组的频数为——
,频率为————。
20
40﹪
在2、5、6、8、4、2、0、1、9、2、3、5
十二个数据中
2的频数是 ( ) , 2的频率是( )
0的频数是 ( ) , 0的频率是( )
3
0.25
1
各种牌子的雪糕应进多少?
你能帮李大爷想想办法吗?
帮李大爷进“货”
小丽统计了最近一个星期李大爷每天平均能卖出的A、B、C、D、E五个牌子的雪糕的数量,并绘制出下图。
关注数据
根据小丽的统计结果,请你为李大爷设计一个进货方案.
象这样的统计图称为频数分布直方图.
平均每天平均能卖出的雪糕的数量
A
B
C
200
150
100
50
D
D
雪糕的品种
131
182
68
39
98
频数分布主要研究数据的分布规律,它研究这些个体在和个小范围内所占比例的大小,便于对数据的分布情况做出全面的估计
一表知“情”
现场调查某班50名同学们的身高(单位cm),并填写下表:
141 165 144 171 145 145 158 150 157 150
154 168 168 155 155 169 157 157 157 158
149 150 150 160 152 152 159 152 159 144
154 155 157 145 160 160 160 158 162 155
162 163 155 163 148 163 168 155 145 172
做一做P161
通过计算,我们可以求出这组数据的平均数,以此来了解这批学生的平均身高。但有时只知道这些数据还不够,还希望知道身高在哪个小范围内的学生多,哪个小范围内的学生少。为此我们需要对这种数据进行整理。
1.计算极差:
3.确定分点:
2.定距,分组:
4.用唱票的方法绘制频数分布表
5.绘制频数分布直方图;
身高x/cm 学生数(频数)
140≤x<145
145≤x<150
150≤x<155
155≤x<160
160≤x<165
165≤x<170
170≤x<175
频数分布表
正一
正
3
6
9
16
9
5
2
正
正
正正正一
身高 141 142 143 144 145 146 147 148 149 150 151
学生数
身高 152
153 154 155 156 157 158 159 160 161 162
学生数
身高 163 164 165 166 167 168 169 170 171 172
学生数
整理数据时,我们可以按照下面的步骤进行:
1。计算最大值与最小值的差(即这组数据的极差)
在本题中最高身高为172厘米,最低身高为141厘米,则极差=172-141=31厘米
2。决定组距与组数
组距是指每个小组的两个端点之间的距离,为了表示的方便习惯上组距可取5或者10,当然这也不是绝对的。
组数=极差÷组距。如31 ÷5=6……1取整数,则这组整数分为7组。
3。决定分点
为了避免数据的交叉,目前公认的方法有2种:
(1)使分点比数据多一位小数,且把第一组的起点稍微减少一点。如第一组为140.5~145.5,第二组为145.5~150.5,…..第七组为170.5~175.5
(2)可采用半闭半开区间法,此外为了保持组距相等,我们可把最小值减少一点作为最左端的分点,把最大值加大一点作为最右端的分点。如本题的最左端点可取为140厘米,最右端点为175(140+5×7=175)厘米。则第一组为140≤身高<145,第二组为145≤身高<150, …..,第七组为170 ≤身高<175。
并由此绘制出频数分布直方图:
你能从上面的频数分布直方图中估计出小明班上同学的平均身高数吗?
0
5
10
15
20
140 145 150 155 160 165 170 175 身高/cm
3
16
9
9
5
6
2
连续型统计量的频数分布直方图
学生人数
我们还可以在得到的频数分布直方图上取点、连线,
得到如下的频数折线图
某校八年级(1)班学生期中考试数学成绩如下(单位:分)
77 59 94 87 90 70 82 85 87 77 74
82 82 95 82 85 87 74 68 84 80 65
92 80 85 82 77 92 98 77 60 74 82
82 80 90 100 67 84 76 56 63 70 89 78
列出数据频数分布表,绘出频数分布直方图及折线图
补充例题
1。计算极差
2。决定组距和和组数。
3。确定分点
4。列频数分布表
极差=100-56=44(分)
组数=44÷5=8.8 取整数,这组数据分为9组
最左端分点可取55分,最右端分点为100(55+5×9=100)(分)
成绩x/分 学生数(频数) 频率
55 ≤x<60 2 0.042
60 ≤x<65 2 0.042
65 ≤x<70 3 0.063
70 ≤x<75 6 0.125
75 ≤x<80 7 0.146
80 ≤x<85 12 0.250
85 ≤x<90 8 0.167
90 ≤x<95 5 0.104
95 ≤x≤100 3 0.062
合计 48 1.00
频数分布表
5。画出频数分布直方图及频数分布折线图
65
75
80
90
7
3
0
3
6
9
12
15
55
60
70
85
95
100
2
2
6
12
8
5
3
成绩(分)
学生人数(人)
频数分布直方图
频数分布折线图
展现自我
储蓄所太多必将增加银行的支出,太少又难以满足顾客需求,银行在在某储蓄所抽样调查了50名顾客,他们的等待时间(进入银行到接受受理的时间间隔,单位:min)如下:
这50名顾客的平均等待时间是多少?根据这个数据,你义为应该给银行提什么建议?
将数据适当分组,绘制相应的频数分布直方图;
随堂练习P166
15 20 18 3 25 34 6 0 17 24
23 30 35 42 37 24 21 1 14 12
34 22 13 34 8 22 31 24 17 33
4 14 23 32 33 28 42 25 14 22
31 42 34 26 14 25 40 14 24 11
绘制连续型频数分布直方图的步骤:
(1)计算极差(最大值与最小值的差);
(2)决定组距(每个小组的两个端点之间的距离)与组数;(关键)
(3)确定分点;
(4)列频数分布表;
(5)画频数分布直方图.
当数据在100个以内时,通常分成5-12组,组距通常取整数
小亮用的是半闭半开区间 (即包含最小值不含最大值)
频数分布表
目标检 测:
1.在对60个数据进行整理的频数分布表中,各组的频数之和为_________,各组的频率之和为_________。
2.一个样本有100个数据,其中最大值是7.4,最小值是4 ,若组距为0.3则这组数据为_____
组。
60
1
12
2、如图所示,是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共70个,请回答下列问题:
(1)本周“百姓热线”共接到热线电话多少个?
(2)有关道路交通问题的电话有多少个?
奇闻逸事
其他投诉
道路交通
环境保护
房产建筑
表扬建议
0 5% 10% 15% 20% 25% 30% 35%
19. (2007深圳中考题6分 ) 2007年某市国际车展期间,某公司对参观本次车展盛会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部收回.①根据调查问卷的结果,将消费者年收入的情况整理后,制成表格如下:
年收入(万元) 4.8 6 7.2 9 10
被调查的消费者人数(人) 200 500 200 70 30
②将消费者打算购买小车的情况整理后,作出频数分布直方图的一部分(如图4).注:每组包含最小值不包含最大值,且车价取整数.请你根据以上信息,回答下列问题:
(1)根据①中信息可得,被调查消费者
的年收入的众数是 万元.
(2)请在图4中补全这个频数分布直方图.
4
6
8
10
12
14
人数 / 人
车价 / 万元
360
200
120
40
0
16
图4
(3)打算购买价格10万元以下小车的消费者人数占被调查消费者人数的百分比是 .
中考链接
19. (2007深圳中考题6分 ) 2007年某市国际车展期间,某公司对参观本次车展盛会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部收回.①根据调查问卷的结果,将消费者年收入的情况整理后,制成表格如下:
年收入(万元) 4.8 6 7.2 9 10
被调查的消费者人数(人) 200 500 200 70 30
②将消费者打算购买小车的情况整理后,作出频数分布直方图的一部分(如图4).注:每组包含最小值不包含最大值,且车价取整数.请你根据以上信息,回答下列问题:
4
6
8
10
12
14
人数 / 人
车价 / 万元
360
200
120
40
0
16
图4
6
(1)根据①中信息可得,被调查消费者的年收入的众数是 万元.
年收入(万元) 4.8 6 7.2 9 10
被调查的消费者人数(人) 200 500 200 70 30
②将消费者打算购买小车的情况整理后,作出频数分布直方图的一部分(如图4).注:每组包含最小值不包含最大值,且车价取整数.请你根据以上信息,回答下列问题:
(2)请在图4中补全这个频数分布直方图.
4
6
8
10
12
14
人数 / 人
车价 / 万元
360
200
120
40
0
16
图4
(3)打算购买价格10万元以下小车的消费者人数占被调查消费者人数的百分比是 .
52﹪
19、(2005年深圳市中考试题8分)右图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图。
(1)求该班有多少名学生?
(2)补上步行分布直方图的空缺部分;
(3)在扇形统计图中,求骑车人数所占的圆心角度数。
(4)若全年级有500人,估计该年级步行人数。
20
12
8
乘车
步行
骑车
乘车50%
步行
20%
骑车
30%
知识的升华
独立
作业
结束寄语
最好的应用数学是与最好的纯数学同样深奥、美妙和有趣.
频数、频率、频数分布表、频数分布直方图和频数分布折线图都反映了一组数据的分布情况.
在学习和生活中体会数学的“简捷”性.
再 见!
*
第一课时
济宁十二中 陈伟利
人们常用哪三种统计图表示一组数据?
扇形统计图
条形统计图
折线统计图
扇形统计图能清楚地表示出各部分在总体中所占的百分比.
扇形统计图有什么特点?
条形统计图能清楚地表示出每个项目的具体数目。
某校300名学生回校方式统计图
条形统计图有什么特点?
1957 1974 1987 1999 2025 2050
折线统计图有什么特点?
折线统计图能清楚地反映事物的变化情况。
1、某专业户要出售100只羊,现在市场上羊的价格为每千克11元,为了估计这100只羊能卖多少钱,该专业户从中随机抽取5只羊,每只羊的质量如下(单位:千克):26,31,32,36,37.
(1)估计这100只羊每只的平均价格;
(2)估计这100只羊一共能卖多少钱?
巩固习题
解析:(1)先求出5只羊中每只羊的平均质量,从而估计100只羊的平均质量;
(2)先估计100只羊的总质量,再乘一每千克的价格,即为所求。
(1)X=1/5(26+31+32+36+37)=32.4(kg)
所以估计这100只羊的平均质32.4kg。
(2)32.4×100×11=35640(元)
所以估计这100只羊一共能卖35640。
2:李敏的爸爸在山上种了橙果树44株,现进入收获期,收获时,先随意采摘5株果树上的橙子,称得每株果树上橙子的质量如下(单位:kg)
35,35,34,39,37.
(1)在这个问题中,总体、样本各是什么 ?
(2)若市场上橙子售价为每千克5元,则这年李敏家卖橙子收入将达多少元?
巩固习题
(1)44株橙果树的质量是总体
采摘的5株果树上的橙子的质量是总体的一个样本
(2)x=1/5(35+35+34+39+37)
=36(kg)
36×44×5=7920(元)
小结 拓展
C
D
B
A
频数与频率
你喜欢看足球比赛吗?你喜欢的足球明星是谁?
小明调查了八(1)班50名同学最喜欢的足球明星,结果如下: (其中A代表贝克汉母,B代表费戈,C代表罗纳尔多,D代表巴乔).
领悟新知
A A B C D A B A A C
B A A C B C A A B C
A A B A C D A A C D
B A C D A A A C D A
C B A A C C D A A C
有无捷径
一目了然
根据这个结果,你能很快说出该班同学最喜欢的足球明星吗?
领悟新知
你认为小明的数据表示方式好不好?你能设计出一个比较好的表示方式吗?
A A B C D A B A A C
B A A C B C A A B C
A A B A C D A A C D
B A C D A A A C D A
C B A A C C D A A C
象这样的表格称为频数分布表.它可以用唱票的方法来制作.
一表知“情”
小丽根据小明的结果,制成了下面的图表,你能从中迅速判断出该班同学最喜欢的足球明星吗?
关注数据
足球明星 学生数
A 正正正正 23
B 正 8
C 正正 13
D 正一 6
明星
学生人数
A
B
C
25
20
15
10
5
D
象这样的图称为频数分布直方图.
一数知“情”
开启智慧
从上表可以看出,A,B,C,D出现的次数有的多,有的少,或者说它们出现的频繁程度不同.我们称每个对象出现的次数为频数(absolute frequency),而每个对象出现的次数与总次数的比值为频率(relative frequency).
如,A的频数为23.A的频率为23/50或 .
足球明星 学生数
A 正正正正 23
B 正 8
C 正正 13
D 正一 6
频率=
频数
总次数
频数=
频数,频率和总个数之间的公式:
总次数=
频率
频数
频率 X 总次数
练习 :
1.某班60名同学中,身高为1.50米—1.65米的人数为12人,那么这组数据的频数是___,频率是____.
2.某班学生参加考试,分数是60-70分的组的人数20,该组的频率是0.20,则这班有__人.
3.为了了解某单位青年人现在对自己所从事工作的满意程度,小明随机调查了该单位一批青年,数所据如下(1表不满意,2表示不满意,3表示一般,4表示满意,5表示很满意):
2 5 4 5 2 5 3 1 2 3
4 4 3 3 5 2 1 4 3 3
3 4 4 2 5 5 4 4 4 2
3 2 4 3 3 5 1 1 5 3
4 1 2 2 3 4 3 3 1 4
根据上述信息填右表;你认为该单位青年人现在对自己所从事工作的满意吗
调查情况 频数 频率
很不满意
不满意
一般
满意
很满意
合计
练习:为了了解某种小麦麦穗的长度,科技人员抽测实验田麦穗 的长度,列表如下:
(1)表中未完成部分:
a=__,b=__,c=__,d=__,
e=__,f=__,g=____.
(2)该问题的总体是_______;
个体是_____________;
样本是_____________.
(3)所测样本中共有___数据.
长度在5.95—6.45cm的麦穗
占总数的百分之几 ______.
(5)众数在_____组,中位数在_____组.
组数 分组 频数 频率
1 4.45—4.95 a 0.05
2 4.95—5.45 2 e
3 5.45—5.95 6 0.30
4 5.95—6.45 b f
5 6.45—6.95 c 0.25
合计 d g
“频率”知多少
看法相同的同学组成一个小组,设计一个简单的调查方案,粗略地估计一下它的使用频率,并将调查结果在全班交流 .
你认为哪个汉字的使用频率最高?
做一做
一图知“情”
小明和小亮从同一本书中分别随机抽取了6页,在统计了1页,2页,3页,4页,5页,6页“的”和“了”出现的次数后,分别求出了它们出现的频率,并绘制了下图:
议一议P186
随着统计页数的增加,这两个字出现的频率是如何变化的
你认为该书中“的”和“了”两个字的使用频率哪个高
频率
●
1 2 3 4 5 6
统计的页数
0.06
0.05
0.04
0.03
0.02
0.01
图例:
■的
●了
●
●
●
●
●
■
■
■
■
■
■
象这样的图称为频数分布折线图.
一节课下来:
我最大的收获是______________
我对自己的表现感想如何_____________
我对同伴的感想如何________________
我从同学身上学到了________________
你能用本节课的知识设计一个问题,并设法 解决吗
知识的升华
独立
作业
*
第二课时
济宁十二中 陈伟利
频数与频率
回顾与思考
1。在统计里,我们称每个考查对象出现的次数为——,每个对象出现的次数与总次数的比值为——。
频数
频率
2。各对象的频数之和等于————,各频率之和等于————。
数据总和
单位1
3。已知一个样本中,50个数据分别落在5个组内,第一,二,三,五的数据个数分别为 2,8,15,5,则第四组的频数为——
,频率为————。
20
40﹪
在2、5、6、8、4、2、0、1、9、2、3、5
十二个数据中
2的频数是 ( ) , 2的频率是( )
0的频数是 ( ) , 0的频率是( )
3
0.25
1
各种牌子的雪糕应进多少?
你能帮李大爷想想办法吗?
帮李大爷进“货”
小丽统计了最近一个星期李大爷每天平均能卖出的A、B、C、D、E五个牌子的雪糕的数量,并绘制出下图。
关注数据
根据小丽的统计结果,请你为李大爷设计一个进货方案.
象这样的统计图称为频数分布直方图.
平均每天平均能卖出的雪糕的数量
A
B
C
200
150
100
50
D
D
雪糕的品种
131
182
68
39
98
频数分布主要研究数据的分布规律,它研究这些个体在和个小范围内所占比例的大小,便于对数据的分布情况做出全面的估计
一表知“情”
现场调查某班50名同学们的身高(单位cm),并填写下表:
141 165 144 171 145 145 158 150 157 150
154 168 168 155 155 169 157 157 157 158
149 150 150 160 152 152 159 152 159 144
154 155 157 145 160 160 160 158 162 155
162 163 155 163 148 163 168 155 145 172
做一做P161
通过计算,我们可以求出这组数据的平均数,以此来了解这批学生的平均身高。但有时只知道这些数据还不够,还希望知道身高在哪个小范围内的学生多,哪个小范围内的学生少。为此我们需要对这种数据进行整理。
1.计算极差:
3.确定分点:
2.定距,分组:
4.用唱票的方法绘制频数分布表
5.绘制频数分布直方图;
身高x/cm 学生数(频数)
140≤x<145
145≤x<150
150≤x<155
155≤x<160
160≤x<165
165≤x<170
170≤x<175
频数分布表
正一
正
3
6
9
16
9
5
2
正
正
正正正一
身高 141 142 143 144 145 146 147 148 149 150 151
学生数
身高 152
153 154 155 156 157 158 159 160 161 162
学生数
身高 163 164 165 166 167 168 169 170 171 172
学生数
整理数据时,我们可以按照下面的步骤进行:
1。计算最大值与最小值的差(即这组数据的极差)
在本题中最高身高为172厘米,最低身高为141厘米,则极差=172-141=31厘米
2。决定组距与组数
组距是指每个小组的两个端点之间的距离,为了表示的方便习惯上组距可取5或者10,当然这也不是绝对的。
组数=极差÷组距。如31 ÷5=6……1取整数,则这组整数分为7组。
3。决定分点
为了避免数据的交叉,目前公认的方法有2种:
(1)使分点比数据多一位小数,且把第一组的起点稍微减少一点。如第一组为140.5~145.5,第二组为145.5~150.5,…..第七组为170.5~175.5
(2)可采用半闭半开区间法,此外为了保持组距相等,我们可把最小值减少一点作为最左端的分点,把最大值加大一点作为最右端的分点。如本题的最左端点可取为140厘米,最右端点为175(140+5×7=175)厘米。则第一组为140≤身高<145,第二组为145≤身高<150, …..,第七组为170 ≤身高<175。
并由此绘制出频数分布直方图:
你能从上面的频数分布直方图中估计出小明班上同学的平均身高数吗?
0
5
10
15
20
140 145 150 155 160 165 170 175 身高/cm
3
16
9
9
5
6
2
连续型统计量的频数分布直方图
学生人数
我们还可以在得到的频数分布直方图上取点、连线,
得到如下的频数折线图
某校八年级(1)班学生期中考试数学成绩如下(单位:分)
77 59 94 87 90 70 82 85 87 77 74
82 82 95 82 85 87 74 68 84 80 65
92 80 85 82 77 92 98 77 60 74 82
82 80 90 100 67 84 76 56 63 70 89 78
列出数据频数分布表,绘出频数分布直方图及折线图
补充例题
1。计算极差
2。决定组距和和组数。
3。确定分点
4。列频数分布表
极差=100-56=44(分)
组数=44÷5=8.8 取整数,这组数据分为9组
最左端分点可取55分,最右端分点为100(55+5×9=100)(分)
成绩x/分 学生数(频数) 频率
55 ≤x<60 2 0.042
60 ≤x<65 2 0.042
65 ≤x<70 3 0.063
70 ≤x<75 6 0.125
75 ≤x<80 7 0.146
80 ≤x<85 12 0.250
85 ≤x<90 8 0.167
90 ≤x<95 5 0.104
95 ≤x≤100 3 0.062
合计 48 1.00
频数分布表
5。画出频数分布直方图及频数分布折线图
65
75
80
90
7
3
0
3
6
9
12
15
55
60
70
85
95
100
2
2
6
12
8
5
3
成绩(分)
学生人数(人)
频数分布直方图
频数分布折线图
展现自我
储蓄所太多必将增加银行的支出,太少又难以满足顾客需求,银行在在某储蓄所抽样调查了50名顾客,他们的等待时间(进入银行到接受受理的时间间隔,单位:min)如下:
这50名顾客的平均等待时间是多少?根据这个数据,你义为应该给银行提什么建议?
将数据适当分组,绘制相应的频数分布直方图;
随堂练习P166
15 20 18 3 25 34 6 0 17 24
23 30 35 42 37 24 21 1 14 12
34 22 13 34 8 22 31 24 17 33
4 14 23 32 33 28 42 25 14 22
31 42 34 26 14 25 40 14 24 11
绘制连续型频数分布直方图的步骤:
(1)计算极差(最大值与最小值的差);
(2)决定组距(每个小组的两个端点之间的距离)与组数;(关键)
(3)确定分点;
(4)列频数分布表;
(5)画频数分布直方图.
当数据在100个以内时,通常分成5-12组,组距通常取整数
小亮用的是半闭半开区间 (即包含最小值不含最大值)
频数分布表
目标检 测:
1.在对60个数据进行整理的频数分布表中,各组的频数之和为_________,各组的频率之和为_________。
2.一个样本有100个数据,其中最大值是7.4,最小值是4 ,若组距为0.3则这组数据为_____
组。
60
1
12
2、如图所示,是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共70个,请回答下列问题:
(1)本周“百姓热线”共接到热线电话多少个?
(2)有关道路交通问题的电话有多少个?
奇闻逸事
其他投诉
道路交通
环境保护
房产建筑
表扬建议
0 5% 10% 15% 20% 25% 30% 35%
19. (2007深圳中考题6分 ) 2007年某市国际车展期间,某公司对参观本次车展盛会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部收回.①根据调查问卷的结果,将消费者年收入的情况整理后,制成表格如下:
年收入(万元) 4.8 6 7.2 9 10
被调查的消费者人数(人) 200 500 200 70 30
②将消费者打算购买小车的情况整理后,作出频数分布直方图的一部分(如图4).注:每组包含最小值不包含最大值,且车价取整数.请你根据以上信息,回答下列问题:
(1)根据①中信息可得,被调查消费者
的年收入的众数是 万元.
(2)请在图4中补全这个频数分布直方图.
4
6
8
10
12
14
人数 / 人
车价 / 万元
360
200
120
40
0
16
图4
(3)打算购买价格10万元以下小车的消费者人数占被调查消费者人数的百分比是 .
中考链接
19. (2007深圳中考题6分 ) 2007年某市国际车展期间,某公司对参观本次车展盛会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部收回.①根据调查问卷的结果,将消费者年收入的情况整理后,制成表格如下:
年收入(万元) 4.8 6 7.2 9 10
被调查的消费者人数(人) 200 500 200 70 30
②将消费者打算购买小车的情况整理后,作出频数分布直方图的一部分(如图4).注:每组包含最小值不包含最大值,且车价取整数.请你根据以上信息,回答下列问题:
4
6
8
10
12
14
人数 / 人
车价 / 万元
360
200
120
40
0
16
图4
6
(1)根据①中信息可得,被调查消费者的年收入的众数是 万元.
年收入(万元) 4.8 6 7.2 9 10
被调查的消费者人数(人) 200 500 200 70 30
②将消费者打算购买小车的情况整理后,作出频数分布直方图的一部分(如图4).注:每组包含最小值不包含最大值,且车价取整数.请你根据以上信息,回答下列问题:
(2)请在图4中补全这个频数分布直方图.
4
6
8
10
12
14
人数 / 人
车价 / 万元
360
200
120
40
0
16
图4
(3)打算购买价格10万元以下小车的消费者人数占被调查消费者人数的百分比是 .
52﹪
19、(2005年深圳市中考试题8分)右图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图。
(1)求该班有多少名学生?
(2)补上步行分布直方图的空缺部分;
(3)在扇形统计图中,求骑车人数所占的圆心角度数。
(4)若全年级有500人,估计该年级步行人数。
20
12
8
乘车
步行
骑车
乘车50%
步行
20%
骑车
30%
知识的升华
独立
作业
结束寄语
最好的应用数学是与最好的纯数学同样深奥、美妙和有趣.
频数、频率、频数分布表、频数分布直方图和频数分布折线图都反映了一组数据的分布情况.
在学习和生活中体会数学的“简捷”性.
再 见!
