沪科版(2019)物理 必修第二册 3.3 圆周运动的案例分析 培优训练(含解析)
文档属性
| 名称 | 沪科版(2019)物理 必修第二册 3.3 圆周运动的案例分析 培优训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 144.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览



文档简介
高中物理沪科版(2019)必修第二册第3章圆周运动-3.3圆周运动的案例分析培优训练
一、单选题
1.关于铁路弯道的设计及火车安全通过弯道时,下列说法正确的是(?? )
A.?内、外轨一样高?????????B.?内轨略高于外轨?????????C.?火车转弯时应当减速?????????D.?火车转弯时应当加速
2.如图所示,质量为m的小物体沿着半径为r的半圆形轨道滑到最低点时的速度大小为v,若物体与轨道之间的动摩擦因数为μ,则小物体刚滑到最低点时(?? )
A.?所受合力方向指向圆心 B.?所受重力的功率为 mgv
C.?所受合力的大小为 mv2r D.?所受摩擦力的大小为 μm(g+v2r)
3.在光滑四分之一圆弧轨道的顶端 a 点,质量为 m 的物块(可视为质点)由静止开始下滑,经圆弧最低点 b 滑上粗糙水平面,圆弧轨道在 b 点与水平轨道平滑相接,物块最终滑至 c 点停止。若圆弧轨道半径为 R ,物块与水平面间的动摩擦因数为 μ ,下列说法错误的是(?? )
A.?物块滑到 b 点时的速度为 3gR??????????????????????B.?物块滑到圆弧轨道的 b 点时对 b 点的压力是 3mg
C.?c 点与 b 点的距离为 Rμ??????????????????????????????????? D.?整个过程中物块机械能损失了 mgR
4.如图所示,细轻杆的一端与小球相连,可绕O点的水平轴自由转动。 现给小球一初速度,使它在竖直平面内做圆周运动,a、b 分别表示轨道的最低点和最高点,则小球在这两点对杆的作用力大小之差不可能为(?? )
A.?3mg????????????????????????????????????B.?4mg????????????????????????????????????C.?5mg????????????????????????????????????D.?6mg
5.公路转弯处外侧的李先生家门口,连续发生了多起车辆侧翻的事故。经交警调查,画出的现场示意图如图所示。为了避免车辆侧翻事故再次发生,很多人提出了建议,下列建议中合理的是(?? )
①提醒司机不要超速转弯??????? ②提醒司机以更小半径转弯
③增大车轮与路面间的粗糙程度? ④使弯道路面内侧低外侧高
A.?①②③?????????????????????????????????B.?①③④?????????????????????????????????C.?②③④?????????????????????????????????D.?②③
6.如图,一质量为M的光滑大圆环,用一细轻杆固定在竖直平面内;套在大圆环上的质量为m的小环(可视为质点),从大圆环的最高处由静止滑下,重力加速度为g.当小圆环滑到大圆环的最低点时,大圆环对轻杆拉力的大小为( ??)
A.?Mg-5mg?????????????????????????B.?Mg+mg?????????????????????????C.?Mg+5mg?????????????????????????D.?Mg+10mg
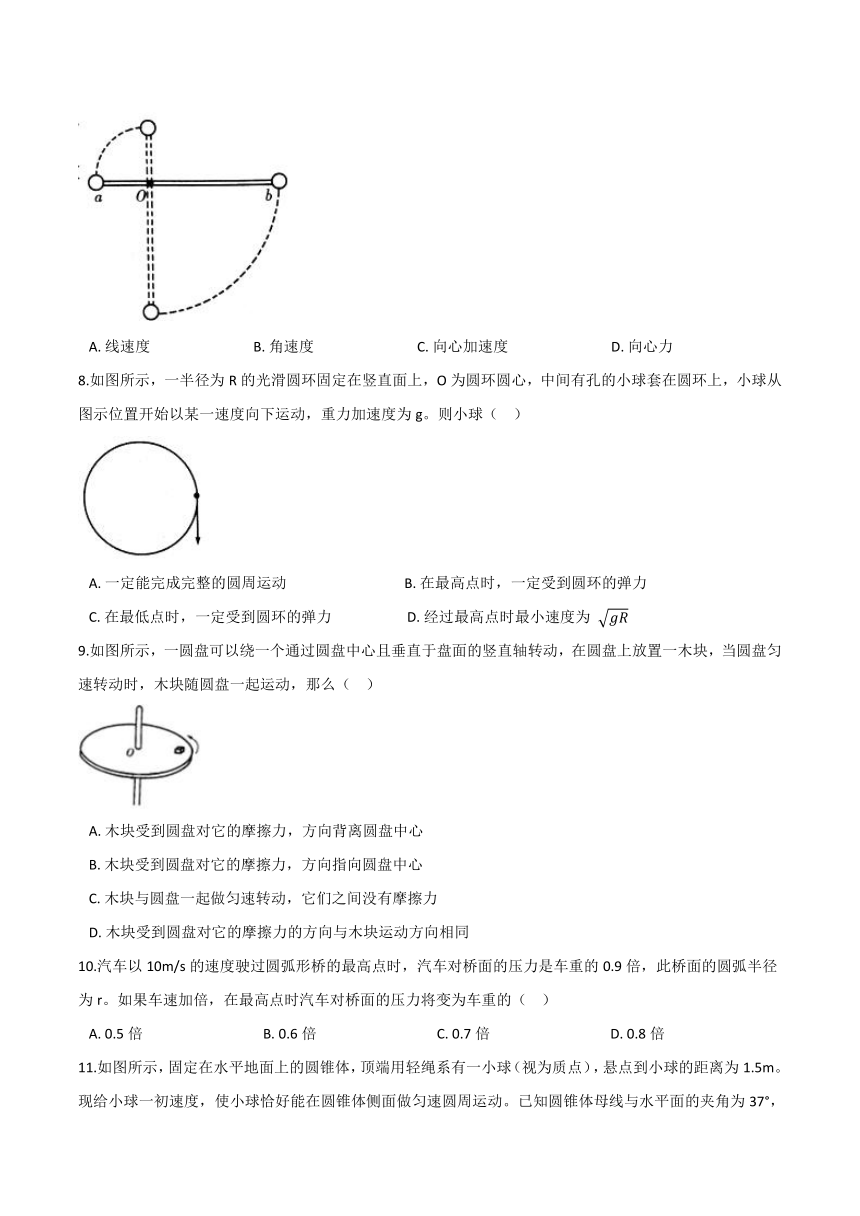
7.如图所示,一轻杆两端a、b分别固定两个完全相同的小球,杆可绕水平固定轴的O点在竖直面内自由转动,Ob的长度大于Oa的长度。初始时,杆处于水平位置,从图示位置释放,在杆转动 π2 的过程中,两小球的以下物理量大小时刻相等的是(?? )
A.?线速度??????????????????????????????B.?角速度??????????????????????????????C.?向心加速度??????????????????????????????D.?向心力
8.如图所示,一半径为R的光滑圆环固定在竖直面上,O为圆环圆心,中间有孔的小球套在圆环上,小球从图示位置开始以某一速度向下运动,重力加速度为g。则小球(?? )
A.?一定能完成完整的圆周运动???????????????????????????????? B.?在最高点时,一定受到圆环的弹力
C.?在最低点时,一定受到圆环的弹力??????????????????????D.?经过最高点时最小速度为 gR
9.如图所示,一圆盘可以绕一个通过圆盘中心且垂直于盘面的竖直轴转动,在圆盘上放置一木块,当圆盘匀速转动时,木块随圆盘一起运动,那么(?? )
A.?木块受到圆盘对它的摩擦力,方向背离圆盘中心
B.?木块受到圆盘对它的摩擦力,方向指向圆盘中心
C.?木块与圆盘一起做匀速转动,它们之间没有摩擦力
D.?木块受到圆盘对它的摩擦力的方向与木块运动方向相同
10.汽车以10m/s的速度驶过圆弧形桥的最高点时,汽车对桥面的压力是车重的0.9倍,此桥面的圆弧半径为r。如果车速加倍,在最高点时汽车对桥面的压力将变为车重的( ??)
A.?0.5倍???????????????????????????????????B.?0.6倍???????????????????????????????????C.?0.7倍???????????????????????????????????D.?0.8倍
11.如图所示,固定在水平地面上的圆锥体,顶端用轻绳系有一小球(视为质点),悬点到小球的距离为1.5m。现给小球一初速度,使小球恰好能在圆锥体侧面做匀速圆周运动。已知圆锥体母线与水平面的夹角为37°,取sin37°=0.6,cos37°=0.8,重力加速度大小g=10m/s2 , 不计空气阻力。则小球做匀速圆周运动的线速度大小为(?? )
A.?2m/s???????????????????????????????????B.?4m/s???????????????????????????????????C.?5m/s???????????????????????????????????D.?6m/s
12.质量为m的小球,用一条绳子系在竖直平面内做圆周运动,小球到达最高点时的速度为v,到达最低点时的速变为 ,则两位置处绳子所受的张力之差是( ??)
A.?6mg????????????????????????????????????B.?5mg????????????????????????????????????C.?4mg????????????????????????????????????D.?2mg
二、填空题
13.质量为1.0?103kg的汽车,行驶至一半径为100m的拱桥顶点时,当该车速度达到________ m/s时,汽车对桥顶的压力为零。(g=10m/s2)
14.如图所示,两个完全相同的小球A、B用长为l="0.8" m的细绳悬于以v="4" m/s向右匀速运动的小车顶部,两小球分别与小车的前后壁接触.由于某种原因,小车突然停止,此时悬线中的张力之比为________
15.质量为m的汽车经过凸拱桥顶点时的速度为v,桥面可看成圆弧,半径为r,汽车受桥面的支持力的大小为________,当汽车经过凸拱桥顶点时的速度为________时,桥面对汽车的支持力为零。(已知重力加速度为g)
16.如图所示,一辆匀速行驶汽车,通过水平路面时对路面的压力________(填“大于”“等于”或“小于”)汽车的重力;通过凹形路面最低处时对路面的压力________(填“大于”“等于”或“小于”)汽车的重力.
三、综合题
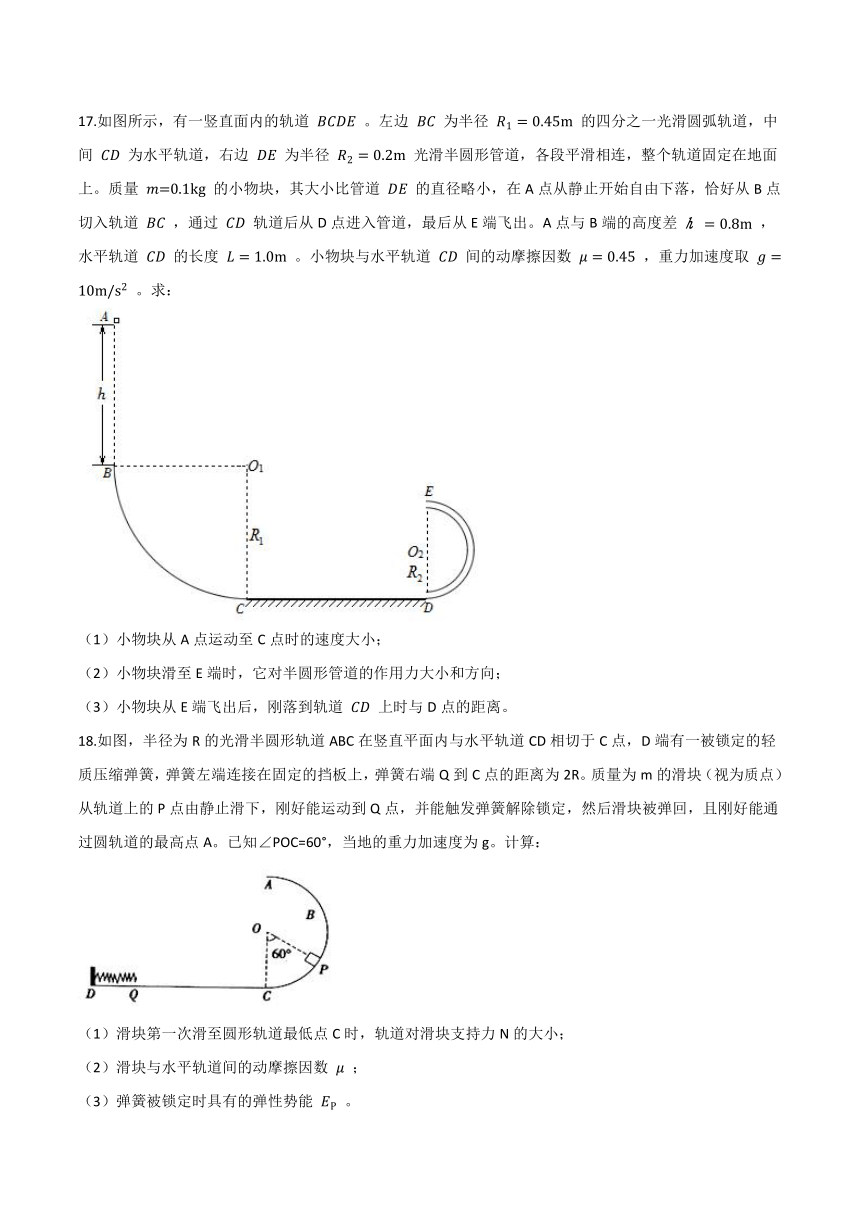
17.如图所示,有一竖直面内的轨道 BCDE 。左边 BC 为半径 R1=0.45m 的四分之一光滑圆弧轨道,中间 CD 为水平轨道,右边 DE 为半径 R2=0.2m 光滑半圆形管道,各段平滑相连,整个轨道固定在地面上。质量 m=0.1kg 的小物块,其大小比管道 DE 的直径略小,在A点从静止开始自由下落,恰好从B点切入轨道 BC ,通过 CD 轨道后从D点进入管道,最后从E端飞出。A点与B端的高度差 h=0.8m ,水平轨道 CD 的长度 L=1.0m 。小物块与水平轨道 CD 间的动摩擦因数 μ=0.45 ,重力加速度取 g=10m/s2 。求:
(1)小物块从A点运动至C点时的速度大小;
(2)小物块滑至E端时,它对半圆形管道的作用力大小和方向;
(3)小物块从E端飞出后,刚落到轨道 CD 上时与D点的距离。
18.如图,半径为R的光滑半圆形轨道ABC在竖直平面内与水平轨道CD相切于C点,D端有一被锁定的轻质压缩弹簧,弹簧左端连接在固定的挡板上,弹簧右端Q到C点的距离为2R。质量为m的滑块(视为质点)从轨道上的P点由静止滑下,刚好能运动到Q点,并能触发弹簧解除锁定,然后滑块被弹回,且刚好能通过圆轨道的最高点A。已知∠POC=60°,当地的重力加速度为g。计算:
(1)滑块第一次滑至圆形轨道最低点C时,轨道对滑块支持力N的大小;
(2)滑块与水平轨道间的动摩擦因数 μ ;
(3)弹簧被锁定时具有的弹性势能 EP 。
19.如图所示,有一个可视为质点的质量m=1kg的小物块,从光滑平台上的A点以v0=1.8m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在竖直平面内的光滑圆弧轨道。圆弧轨道的半径为R=2m,C点和圆弧的圆心O点连线与竖直方向的夹角θ=53°,不计空气阻力,重力加速度g=10m/s2 , sin53°=0.8,cos53°=0.6。求:
(1)光滑平台上的A点到BC平面的高度;
(2)小物块到达圆弧轨道最低点D时对轨道的压力。
参考答案
1.【答案】 C
【解析】AB.铁路转弯时,一般外轨略高于内轨,这样支持力的水平分力提供一部分火车做圆周运动的向心力,因此AB不符合题意;
C.火车转弯时,为了安全,一般减速运动,使火车所需向心力减少,从而减少对外轨的压力,C符合题意,D不符合题意。
故答案为:C。
2.【答案】 D
【解析】A.小物体滑到最低点时,对小物体受力分析,由向下的重力、向上轨道的支持力和水平向左的摩擦力,所以小物块此时所受合力方向一定不是指向圆心,所以A不符合题意;
B.据功率的表达式 P=Fvcosθ
可得,此时小物块所受重力的功率为 P=Gvcosθ
θ 为重力与速度的夹角,由于此时两者垂直,所以 θ=90?
得 P=0 即此时小物块所受重力的功率为0,所以B不符合题意;
C.物块在做圆周运动,在最低点,根据牛顿第二定律可得 Fn合=mv2r
所以 mv2r 是小物块所受的半径方向的合力,所以C不符合题意;D.据滑动摩擦力的计算公式,有 Ff=μFN
由C选项分析可得,在最低点 Fn合=mv2r
其中 Fn合=FN-mg
则 FN=Fn合+mg=mg+mv2r
得 Ff=μFN=μm(g+v2r)
所以D符合题意。
故答案为:D。
3.【答案】 A
【解析】A.物块从 a→b ,根据机械能守恒定律 mgR=12mv2
解得物块在 b 点速度为 v=2gR
A错误,符合题意;
B.在圆弧轨道 b 点,根据牛顿第二定律 N-mg=mv2R
解得 N=3mg
根据牛顿第三定律可知物块滑到圆弧轨道的 b 点时对 b 点的压力是 3mg ,B正确,不符合题意;
C.物体从 a→c ,根据动能定理可知 mgR-μmgxcb=0
解得 xcb=Rμ
C正确,不符合题意;
D.物体在运动过程中,摩擦力做负功,机械能减小,所以机械能的减少量为 ?E=μmgxcb=mgR
D正确,不符合题意。
故答案为:A。
4.【答案】 A
【解析】设杆长为L,在a点,杆对球的拉力与重力的合力提供向心力,A处杆对球的作用力一定时拉力;则 Fa-mg=mva2R
Fa=mg+mva2R
而在b处,由球速大小决定杆对球的作用力可能为拉力、推力,也可能没有作用力。当杆不产生作用力时 Tb=0
mg=mvb2R
得 vb=gL
当产生拉力时 Tb+mg=mvb2L
这时 Tb=mg+mvb2L
当产生推力时 mg-Tb=mvb2L
这时 Tb=mg-mvb2L
由动能定理得 mg×2L=12mva2-12mvb2
由以上解得 4mg本题选不可能的,故答案为:A。
5.【答案】 B
【解析】①.车发生侧翻是因为外界提供的力不够做圆周运动所需的向心力,发生离心运动;减小速度可以减小需要的向心力,可以防止侧翻现象,故①正确;
②.根据 μmg=mv2r 可知,半径越小,需要的向心力越大,越容易翻车,故②错误;
③.在水平路面上拐弯时,靠静摩擦力提供向心力,可以通过改进路面设计,增大车轮与路面间的摩擦力,可以避免卡车侧翻事故再次发生,故③正确;
④.易发生侧翻也可能是路面设计不合理,应改造路面使内侧低,外侧高,使重力与支持力的合力沿水平方向有向里的分量,故④正确。
故答案为:B。
6.【答案】 C
【解析】小圆环到达大圆环低端时满足: mg?2R=12mv2 ,对小圆环在最低点,有牛顿定律可得: FN-mg=mv2R ;对大圆环,由平衡可知: FT=Mg+FN ,解得 FT=Mg+5mg ,C符合题意.
故答案为:C
7.【答案】 B
【解析】AB.两小球随轻杆转动,属同轴转动,故角速度相等。Ob的长度大于Oa的长度,由线速度公式 v=rω 可知b球线速度大于a球线速度,A不符合题意,B符合题意;
CD.两球角速度相等,b球转动半径大于a球转动半径,由加速度公式 a=rω2 ,可知b球向心加速度大于a球向心加速度,两球质量相同,由向心力公式 F=ma 可知b球向心力大于a球向心力,CD不符合题意。
故答案为:B。
8.【答案】 C
【解析】A.圆环要能做完整的圆周运动,需要满足最高点,最小速度为零,小球从图示位置以某一速度运动,有可能到不了最高点,A不符合题意;
B.在最高点,速度如果等于 gR ,圆环对小球没有作用力,速度如果小于 gR ,小球受到圆环向上的弹力,速度如果大于 gR ,小球受到圆环向下的弹力,B不符合题意;
C.在最低点,小球受到向上的弹力、重力,合力提供向心力,故在最低点时,一定受到圆环的弹力,C符合题意;
D.小球是套在圆环上的,经过最高点时最小速度为0,D不符合题意。
故答案为:C。
速度结合向心力公式求解小球对圆轨道的作用力。
9.【答案】 B
【解析】木块随圆盘一起做匀速圆周运动,所受合力指向圆心,作为木块做匀速圆周运动的向心力,而这个向心力就是摩擦力提供的,因此木块受到圆盘对它的摩擦力,方向指向圆盘中心,B符合题意,ACD不符合题意。
故答案为:B。
10.【答案】 B
【解析】根据 mg-FN=mv2r 可得:当汽车的速度为10m/s时: mg-0.9mg=m102r
当车速加倍时: mg-kmg=m202r
联立解得:k=0.6
故答案为:B
11.【答案】 B
【解析】由题意知,当小球重力与绳子拉力的合力刚好提供向心力时,物体与圆锥恰好无压力,即 mgtanθ=mv02Lcosθ
解得 v0=gLcosθtanθ=4m/s
B符合题意,ACD不符合题意。
故答案为:B。
12.【答案】 A
【解析】在最高点,小球受重力和绳子的拉力T1 , 合力提供向心力,根据牛顿第二定律,有: mg+T1=mv2R
在最低点,重力和拉力 T2 ,合力提供向心力,根据牛顿第二定律,有: T2-mg=mv'2R
最低点速度为: v'=4gR+v2
两位置处绳子所受的张力之差为: ΔT=T2-T1 ,联立解得: ΔT=6mg ,A符合题意.
故答案为:A
13.【答案】 1010
【解析】汽车对桥顶的压力为零,根据牛顿第二定律得 mg=mv2R
代入数据解得 v=1010m/s
14.【答案】 3:1
【解析】小车停止的瞬间,B球静止,重力等于拉力,小球A做圆周运动, F-mg=mv2r ,可求出F与重力之比为3:1。
15.【答案】 mg-mv2r;gr
【解析】经过凸拱桥顶点时,根据向心力公式得: mg-F=mv2r
解得: F=mg-mv2r
当桥面对汽车的支持力为零时,只有重力提供向心力: mg=mv2r
解得: v'=gr
16.【答案】 等于;大于
【解析】汽车做直线运动竖直方向受力平恒,汽车所受支持力等于重力,又因为汽车受到的支持力和汽车给地面的压力是作用力和反作用力,所以压力等于重力;当汽车通过凹面时,汽车会出现向心力,向心力在凹面最低点由合力提供,因为向心力在最低点竖直向上,所以设支持力F,F向=F合=F-G , 所以F大于G,即汽车对地面的压力大于重力。
17.【答案】 (1)解:小物块从A点运动至C点时由机械能守恒定律 mg(h+R1)=12mvC2
解得vC=5m/s
(2)解:从A点到E点由动能定理 mg(h+R1-2R2)-μmgL=12mvE2
解得 vE=22m/s
在E点由牛顿第二定律 mg+FN=mvE2R2
解得FN=3N
方向向下,根据牛顿第三定律可知小物块对轨道的作用力竖直向上
(3)解:小物块从E端飞出后做平抛运动,则 2R2=12gt2
x=vEt ?
解得x=0.8m
即刚落到轨道CD上时与D点的距离0.8m。
【解析】(1)对物体进行受力分析,对物体从A点运动到C点的过程应用动能定理求解物体的末速度;
(2)利用动能定理求解物体到达E点的速度,对处在E点的物体进行受力分析,结合此时物体的速度,利用向心力公式求解物体对轨道的压力;
(3)物体做平抛运动,水平方向匀速运动,竖直方向自由落体运动,利用竖直方向的距离求出运动时间,根据初速度求解水平方向的位移。
18.【答案】 (1)解:设滑块第一次滑至C点时的速度为 vC ,对 P→C 过程,由机械能守恒有 mgR(1-cos60°)=12mvC2
解得 vC=gR
在C点处有 N-mg=mvC2R
解得 N=2mg
(2)解:对 C→Q 过程,由功能关系有 12mvC2-μmg?2R=0
解得 μ=0.25
(3)解:滑块在A点时,由牛顿第二定律有 mg=mvA2R
对 Q→C→A 过程,由功能关系有 EP=12mvA2+mg?2R+μmg?2R
解得弹性势能 EP=3mgR
【解析】(1)利用动能定理求解物体到达最低点的速度,对处在最低点的物体进行受力分析,结合此时物体的速度,利用向心力公式求解物体对轨道的压力;
(2)对物体进行受力分析,结合物体的初末速度,对物体的运动过程应用动能定理求解动摩擦因数;
(3)两个物体组成系统能量守恒,利用能量守恒列方程分析求解即可。
19.【答案】 (1)解:设小物块在C点的速度为 vC ,在C点由 vC=v0cosθ
解得 vC=3m/s
从A点至C点,设A点到BC平面高度为h,由机械能守恒可得 12mv02+mgh=12mvC2
代入数据,解得 h=0.88m
(2)解:设小物块在D点速度为 vD ,从C点至D点由动能定理,可得 mgR(1-cosθ)=12mvD2-12mvC2
解得 vD=5m/s
设在D点轨道对小物块的支持力为FN , 有 FN-mg=mvD2R
解得 FN=22.5N
由牛顿第三定律得
小物块在D点时对轨道压力为 FN'=22.5N
向竖直向下
【解析】(1)结合物体末速度的大小和方向求解水平初速度即可;
(2)利用动能定理求解物体到达最低点的速度,对处在最低点的物体进行受力分析,结合此时物体的速度,利用向心力公式求解物体对轨道的压力。
一、单选题
1.关于铁路弯道的设计及火车安全通过弯道时,下列说法正确的是(?? )
A.?内、外轨一样高?????????B.?内轨略高于外轨?????????C.?火车转弯时应当减速?????????D.?火车转弯时应当加速
2.如图所示,质量为m的小物体沿着半径为r的半圆形轨道滑到最低点时的速度大小为v,若物体与轨道之间的动摩擦因数为μ,则小物体刚滑到最低点时(?? )
A.?所受合力方向指向圆心 B.?所受重力的功率为 mgv
C.?所受合力的大小为 mv2r D.?所受摩擦力的大小为 μm(g+v2r)
3.在光滑四分之一圆弧轨道的顶端 a 点,质量为 m 的物块(可视为质点)由静止开始下滑,经圆弧最低点 b 滑上粗糙水平面,圆弧轨道在 b 点与水平轨道平滑相接,物块最终滑至 c 点停止。若圆弧轨道半径为 R ,物块与水平面间的动摩擦因数为 μ ,下列说法错误的是(?? )
A.?物块滑到 b 点时的速度为 3gR??????????????????????B.?物块滑到圆弧轨道的 b 点时对 b 点的压力是 3mg
C.?c 点与 b 点的距离为 Rμ??????????????????????????????????? D.?整个过程中物块机械能损失了 mgR
4.如图所示,细轻杆的一端与小球相连,可绕O点的水平轴自由转动。 现给小球一初速度,使它在竖直平面内做圆周运动,a、b 分别表示轨道的最低点和最高点,则小球在这两点对杆的作用力大小之差不可能为(?? )
A.?3mg????????????????????????????????????B.?4mg????????????????????????????????????C.?5mg????????????????????????????????????D.?6mg
5.公路转弯处外侧的李先生家门口,连续发生了多起车辆侧翻的事故。经交警调查,画出的现场示意图如图所示。为了避免车辆侧翻事故再次发生,很多人提出了建议,下列建议中合理的是(?? )
①提醒司机不要超速转弯??????? ②提醒司机以更小半径转弯
③增大车轮与路面间的粗糙程度? ④使弯道路面内侧低外侧高
A.?①②③?????????????????????????????????B.?①③④?????????????????????????????????C.?②③④?????????????????????????????????D.?②③
6.如图,一质量为M的光滑大圆环,用一细轻杆固定在竖直平面内;套在大圆环上的质量为m的小环(可视为质点),从大圆环的最高处由静止滑下,重力加速度为g.当小圆环滑到大圆环的最低点时,大圆环对轻杆拉力的大小为( ??)
A.?Mg-5mg?????????????????????????B.?Mg+mg?????????????????????????C.?Mg+5mg?????????????????????????D.?Mg+10mg
7.如图所示,一轻杆两端a、b分别固定两个完全相同的小球,杆可绕水平固定轴的O点在竖直面内自由转动,Ob的长度大于Oa的长度。初始时,杆处于水平位置,从图示位置释放,在杆转动 π2 的过程中,两小球的以下物理量大小时刻相等的是(?? )
A.?线速度??????????????????????????????B.?角速度??????????????????????????????C.?向心加速度??????????????????????????????D.?向心力
8.如图所示,一半径为R的光滑圆环固定在竖直面上,O为圆环圆心,中间有孔的小球套在圆环上,小球从图示位置开始以某一速度向下运动,重力加速度为g。则小球(?? )
A.?一定能完成完整的圆周运动???????????????????????????????? B.?在最高点时,一定受到圆环的弹力
C.?在最低点时,一定受到圆环的弹力??????????????????????D.?经过最高点时最小速度为 gR
9.如图所示,一圆盘可以绕一个通过圆盘中心且垂直于盘面的竖直轴转动,在圆盘上放置一木块,当圆盘匀速转动时,木块随圆盘一起运动,那么(?? )
A.?木块受到圆盘对它的摩擦力,方向背离圆盘中心
B.?木块受到圆盘对它的摩擦力,方向指向圆盘中心
C.?木块与圆盘一起做匀速转动,它们之间没有摩擦力
D.?木块受到圆盘对它的摩擦力的方向与木块运动方向相同
10.汽车以10m/s的速度驶过圆弧形桥的最高点时,汽车对桥面的压力是车重的0.9倍,此桥面的圆弧半径为r。如果车速加倍,在最高点时汽车对桥面的压力将变为车重的( ??)
A.?0.5倍???????????????????????????????????B.?0.6倍???????????????????????????????????C.?0.7倍???????????????????????????????????D.?0.8倍
11.如图所示,固定在水平地面上的圆锥体,顶端用轻绳系有一小球(视为质点),悬点到小球的距离为1.5m。现给小球一初速度,使小球恰好能在圆锥体侧面做匀速圆周运动。已知圆锥体母线与水平面的夹角为37°,取sin37°=0.6,cos37°=0.8,重力加速度大小g=10m/s2 , 不计空气阻力。则小球做匀速圆周运动的线速度大小为(?? )
A.?2m/s???????????????????????????????????B.?4m/s???????????????????????????????????C.?5m/s???????????????????????????????????D.?6m/s
12.质量为m的小球,用一条绳子系在竖直平面内做圆周运动,小球到达最高点时的速度为v,到达最低点时的速变为 ,则两位置处绳子所受的张力之差是( ??)
A.?6mg????????????????????????????????????B.?5mg????????????????????????????????????C.?4mg????????????????????????????????????D.?2mg
二、填空题
13.质量为1.0?103kg的汽车,行驶至一半径为100m的拱桥顶点时,当该车速度达到________ m/s时,汽车对桥顶的压力为零。(g=10m/s2)
14.如图所示,两个完全相同的小球A、B用长为l="0.8" m的细绳悬于以v="4" m/s向右匀速运动的小车顶部,两小球分别与小车的前后壁接触.由于某种原因,小车突然停止,此时悬线中的张力之比为________
15.质量为m的汽车经过凸拱桥顶点时的速度为v,桥面可看成圆弧,半径为r,汽车受桥面的支持力的大小为________,当汽车经过凸拱桥顶点时的速度为________时,桥面对汽车的支持力为零。(已知重力加速度为g)
16.如图所示,一辆匀速行驶汽车,通过水平路面时对路面的压力________(填“大于”“等于”或“小于”)汽车的重力;通过凹形路面最低处时对路面的压力________(填“大于”“等于”或“小于”)汽车的重力.
三、综合题
17.如图所示,有一竖直面内的轨道 BCDE 。左边 BC 为半径 R1=0.45m 的四分之一光滑圆弧轨道,中间 CD 为水平轨道,右边 DE 为半径 R2=0.2m 光滑半圆形管道,各段平滑相连,整个轨道固定在地面上。质量 m=0.1kg 的小物块,其大小比管道 DE 的直径略小,在A点从静止开始自由下落,恰好从B点切入轨道 BC ,通过 CD 轨道后从D点进入管道,最后从E端飞出。A点与B端的高度差 h=0.8m ,水平轨道 CD 的长度 L=1.0m 。小物块与水平轨道 CD 间的动摩擦因数 μ=0.45 ,重力加速度取 g=10m/s2 。求:
(1)小物块从A点运动至C点时的速度大小;
(2)小物块滑至E端时,它对半圆形管道的作用力大小和方向;
(3)小物块从E端飞出后,刚落到轨道 CD 上时与D点的距离。
18.如图,半径为R的光滑半圆形轨道ABC在竖直平面内与水平轨道CD相切于C点,D端有一被锁定的轻质压缩弹簧,弹簧左端连接在固定的挡板上,弹簧右端Q到C点的距离为2R。质量为m的滑块(视为质点)从轨道上的P点由静止滑下,刚好能运动到Q点,并能触发弹簧解除锁定,然后滑块被弹回,且刚好能通过圆轨道的最高点A。已知∠POC=60°,当地的重力加速度为g。计算:
(1)滑块第一次滑至圆形轨道最低点C时,轨道对滑块支持力N的大小;
(2)滑块与水平轨道间的动摩擦因数 μ ;
(3)弹簧被锁定时具有的弹性势能 EP 。
19.如图所示,有一个可视为质点的质量m=1kg的小物块,从光滑平台上的A点以v0=1.8m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在竖直平面内的光滑圆弧轨道。圆弧轨道的半径为R=2m,C点和圆弧的圆心O点连线与竖直方向的夹角θ=53°,不计空气阻力,重力加速度g=10m/s2 , sin53°=0.8,cos53°=0.6。求:
(1)光滑平台上的A点到BC平面的高度;
(2)小物块到达圆弧轨道最低点D时对轨道的压力。
参考答案
1.【答案】 C
【解析】AB.铁路转弯时,一般外轨略高于内轨,这样支持力的水平分力提供一部分火车做圆周运动的向心力,因此AB不符合题意;
C.火车转弯时,为了安全,一般减速运动,使火车所需向心力减少,从而减少对外轨的压力,C符合题意,D不符合题意。
故答案为:C。
2.【答案】 D
【解析】A.小物体滑到最低点时,对小物体受力分析,由向下的重力、向上轨道的支持力和水平向左的摩擦力,所以小物块此时所受合力方向一定不是指向圆心,所以A不符合题意;
B.据功率的表达式 P=Fvcosθ
可得,此时小物块所受重力的功率为 P=Gvcosθ
θ 为重力与速度的夹角,由于此时两者垂直,所以 θ=90?
得 P=0 即此时小物块所受重力的功率为0,所以B不符合题意;
C.物块在做圆周运动,在最低点,根据牛顿第二定律可得 Fn合=mv2r
所以 mv2r 是小物块所受的半径方向的合力,所以C不符合题意;D.据滑动摩擦力的计算公式,有 Ff=μFN
由C选项分析可得,在最低点 Fn合=mv2r
其中 Fn合=FN-mg
则 FN=Fn合+mg=mg+mv2r
得 Ff=μFN=μm(g+v2r)
所以D符合题意。
故答案为:D。
3.【答案】 A
【解析】A.物块从 a→b ,根据机械能守恒定律 mgR=12mv2
解得物块在 b 点速度为 v=2gR
A错误,符合题意;
B.在圆弧轨道 b 点,根据牛顿第二定律 N-mg=mv2R
解得 N=3mg
根据牛顿第三定律可知物块滑到圆弧轨道的 b 点时对 b 点的压力是 3mg ,B正确,不符合题意;
C.物体从 a→c ,根据动能定理可知 mgR-μmgxcb=0
解得 xcb=Rμ
C正确,不符合题意;
D.物体在运动过程中,摩擦力做负功,机械能减小,所以机械能的减少量为 ?E=μmgxcb=mgR
D正确,不符合题意。
故答案为:A。
4.【答案】 A
【解析】设杆长为L,在a点,杆对球的拉力与重力的合力提供向心力,A处杆对球的作用力一定时拉力;则 Fa-mg=mva2R
Fa=mg+mva2R
而在b处,由球速大小决定杆对球的作用力可能为拉力、推力,也可能没有作用力。当杆不产生作用力时 Tb=0
mg=mvb2R
得 vb=gL
当产生拉力时 Tb+mg=mvb2L
这时 Tb=mg+mvb2L
当产生推力时 mg-Tb=mvb2L
这时 Tb=mg-mvb2L
由动能定理得 mg×2L=12mva2-12mvb2
由以上解得 4mg
5.【答案】 B
【解析】①.车发生侧翻是因为外界提供的力不够做圆周运动所需的向心力,发生离心运动;减小速度可以减小需要的向心力,可以防止侧翻现象,故①正确;
②.根据 μmg=mv2r 可知,半径越小,需要的向心力越大,越容易翻车,故②错误;
③.在水平路面上拐弯时,靠静摩擦力提供向心力,可以通过改进路面设计,增大车轮与路面间的摩擦力,可以避免卡车侧翻事故再次发生,故③正确;
④.易发生侧翻也可能是路面设计不合理,应改造路面使内侧低,外侧高,使重力与支持力的合力沿水平方向有向里的分量,故④正确。
故答案为:B。
6.【答案】 C
【解析】小圆环到达大圆环低端时满足: mg?2R=12mv2 ,对小圆环在最低点,有牛顿定律可得: FN-mg=mv2R ;对大圆环,由平衡可知: FT=Mg+FN ,解得 FT=Mg+5mg ,C符合题意.
故答案为:C
7.【答案】 B
【解析】AB.两小球随轻杆转动,属同轴转动,故角速度相等。Ob的长度大于Oa的长度,由线速度公式 v=rω 可知b球线速度大于a球线速度,A不符合题意,B符合题意;
CD.两球角速度相等,b球转动半径大于a球转动半径,由加速度公式 a=rω2 ,可知b球向心加速度大于a球向心加速度,两球质量相同,由向心力公式 F=ma 可知b球向心力大于a球向心力,CD不符合题意。
故答案为:B。
8.【答案】 C
【解析】A.圆环要能做完整的圆周运动,需要满足最高点,最小速度为零,小球从图示位置以某一速度运动,有可能到不了最高点,A不符合题意;
B.在最高点,速度如果等于 gR ,圆环对小球没有作用力,速度如果小于 gR ,小球受到圆环向上的弹力,速度如果大于 gR ,小球受到圆环向下的弹力,B不符合题意;
C.在最低点,小球受到向上的弹力、重力,合力提供向心力,故在最低点时,一定受到圆环的弹力,C符合题意;
D.小球是套在圆环上的,经过最高点时最小速度为0,D不符合题意。
故答案为:C。
速度结合向心力公式求解小球对圆轨道的作用力。
9.【答案】 B
【解析】木块随圆盘一起做匀速圆周运动,所受合力指向圆心,作为木块做匀速圆周运动的向心力,而这个向心力就是摩擦力提供的,因此木块受到圆盘对它的摩擦力,方向指向圆盘中心,B符合题意,ACD不符合题意。
故答案为:B。
10.【答案】 B
【解析】根据 mg-FN=mv2r 可得:当汽车的速度为10m/s时: mg-0.9mg=m102r
当车速加倍时: mg-kmg=m202r
联立解得:k=0.6
故答案为:B
11.【答案】 B
【解析】由题意知,当小球重力与绳子拉力的合力刚好提供向心力时,物体与圆锥恰好无压力,即 mgtanθ=mv02Lcosθ
解得 v0=gLcosθtanθ=4m/s
B符合题意,ACD不符合题意。
故答案为:B。
12.【答案】 A
【解析】在最高点,小球受重力和绳子的拉力T1 , 合力提供向心力,根据牛顿第二定律,有: mg+T1=mv2R
在最低点,重力和拉力 T2 ,合力提供向心力,根据牛顿第二定律,有: T2-mg=mv'2R
最低点速度为: v'=4gR+v2
两位置处绳子所受的张力之差为: ΔT=T2-T1 ,联立解得: ΔT=6mg ,A符合题意.
故答案为:A
13.【答案】 1010
【解析】汽车对桥顶的压力为零,根据牛顿第二定律得 mg=mv2R
代入数据解得 v=1010m/s
14.【答案】 3:1
【解析】小车停止的瞬间,B球静止,重力等于拉力,小球A做圆周运动, F-mg=mv2r ,可求出F与重力之比为3:1。
15.【答案】 mg-mv2r;gr
【解析】经过凸拱桥顶点时,根据向心力公式得: mg-F=mv2r
解得: F=mg-mv2r
当桥面对汽车的支持力为零时,只有重力提供向心力: mg=mv2r
解得: v'=gr
16.【答案】 等于;大于
【解析】汽车做直线运动竖直方向受力平恒,汽车所受支持力等于重力,又因为汽车受到的支持力和汽车给地面的压力是作用力和反作用力,所以压力等于重力;当汽车通过凹面时,汽车会出现向心力,向心力在凹面最低点由合力提供,因为向心力在最低点竖直向上,所以设支持力F,F向=F合=F-G , 所以F大于G,即汽车对地面的压力大于重力。
17.【答案】 (1)解:小物块从A点运动至C点时由机械能守恒定律 mg(h+R1)=12mvC2
解得vC=5m/s
(2)解:从A点到E点由动能定理 mg(h+R1-2R2)-μmgL=12mvE2
解得 vE=22m/s
在E点由牛顿第二定律 mg+FN=mvE2R2
解得FN=3N
方向向下,根据牛顿第三定律可知小物块对轨道的作用力竖直向上
(3)解:小物块从E端飞出后做平抛运动,则 2R2=12gt2
x=vEt ?
解得x=0.8m
即刚落到轨道CD上时与D点的距离0.8m。
【解析】(1)对物体进行受力分析,对物体从A点运动到C点的过程应用动能定理求解物体的末速度;
(2)利用动能定理求解物体到达E点的速度,对处在E点的物体进行受力分析,结合此时物体的速度,利用向心力公式求解物体对轨道的压力;
(3)物体做平抛运动,水平方向匀速运动,竖直方向自由落体运动,利用竖直方向的距离求出运动时间,根据初速度求解水平方向的位移。
18.【答案】 (1)解:设滑块第一次滑至C点时的速度为 vC ,对 P→C 过程,由机械能守恒有 mgR(1-cos60°)=12mvC2
解得 vC=gR
在C点处有 N-mg=mvC2R
解得 N=2mg
(2)解:对 C→Q 过程,由功能关系有 12mvC2-μmg?2R=0
解得 μ=0.25
(3)解:滑块在A点时,由牛顿第二定律有 mg=mvA2R
对 Q→C→A 过程,由功能关系有 EP=12mvA2+mg?2R+μmg?2R
解得弹性势能 EP=3mgR
【解析】(1)利用动能定理求解物体到达最低点的速度,对处在最低点的物体进行受力分析,结合此时物体的速度,利用向心力公式求解物体对轨道的压力;
(2)对物体进行受力分析,结合物体的初末速度,对物体的运动过程应用动能定理求解动摩擦因数;
(3)两个物体组成系统能量守恒,利用能量守恒列方程分析求解即可。
19.【答案】 (1)解:设小物块在C点的速度为 vC ,在C点由 vC=v0cosθ
解得 vC=3m/s
从A点至C点,设A点到BC平面高度为h,由机械能守恒可得 12mv02+mgh=12mvC2
代入数据,解得 h=0.88m
(2)解:设小物块在D点速度为 vD ,从C点至D点由动能定理,可得 mgR(1-cosθ)=12mvD2-12mvC2
解得 vD=5m/s
设在D点轨道对小物块的支持力为FN , 有 FN-mg=mvD2R
解得 FN=22.5N
由牛顿第三定律得
小物块在D点时对轨道压力为 FN'=22.5N
向竖直向下
【解析】(1)结合物体末速度的大小和方向求解水平初速度即可;
(2)利用动能定理求解物体到达最低点的速度,对处在最低点的物体进行受力分析,结合此时物体的速度,利用向心力公式求解物体对轨道的压力。
同课章节目录
