六年级数学下册课件-4.1.2 比例的基本性质 人教版(共23张PPT)
文档属性
| 名称 | 六年级数学下册课件-4.1.2 比例的基本性质 人教版(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 19:19:53 | ||
图片预览






文档简介
比例的基本性质
(一)复习旧知
1、什么叫比?比的基本性质是什么?
2.什么叫比例?
(二)自主探究。(预习41页)
1、认识比例各部分的名称。
2、比例各部分的名称和什么有关?怎样记住它们?
3、计算比例中两个外项的积和两个内项的积。比较一下,你能发现什么?
4、你能用字母表示你的发现吗?试一试。
5、比例的基本性质的用途?
复习:
1、什么叫做比?
表示两个比相等的式子叫做比例。
3、什么叫做比例?
两个数相除又叫做两个数的比。
2、什么叫比的基本性质?
比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变.
复习:
4、判断下面每组中的两个比能否组成比例?
(1) 6:15 和 8:20
根据比例的意义判断。
复习:
4、判断下面每组中的两个比能否组成比例?
(2) 0.5 : 0.4 和 2 : 2.5
根据比例的意义判断。
判断两个比能否组成比例,除了用比例的意义之外,还更简单的方法。
1、认识比例各部分的名称。
2、计算比例中两个外项的积和两个内项的积。比较一下,你能发现什么?
3、你能用字母表示你的发现吗?试一试。
4、比例的基本性质的用途?
例如: 2.4 ∶1.6 = 60 ∶40
外项
内项
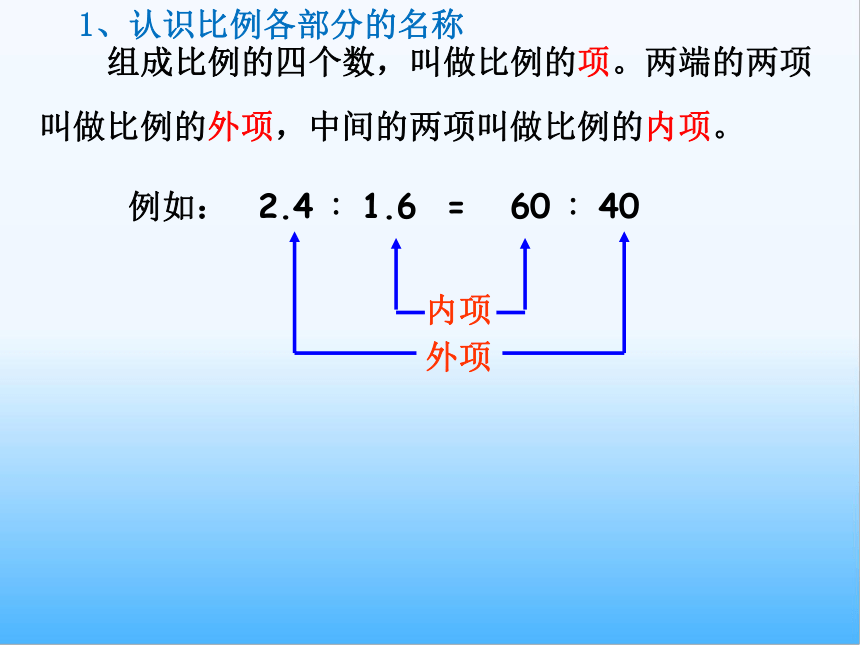
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
1、认识比例各部分的名称
例如: 2.4 ∶1.6 = 60 ∶40
外项
内项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
( )
内项
( )
( )
( )
外项
外项
内项
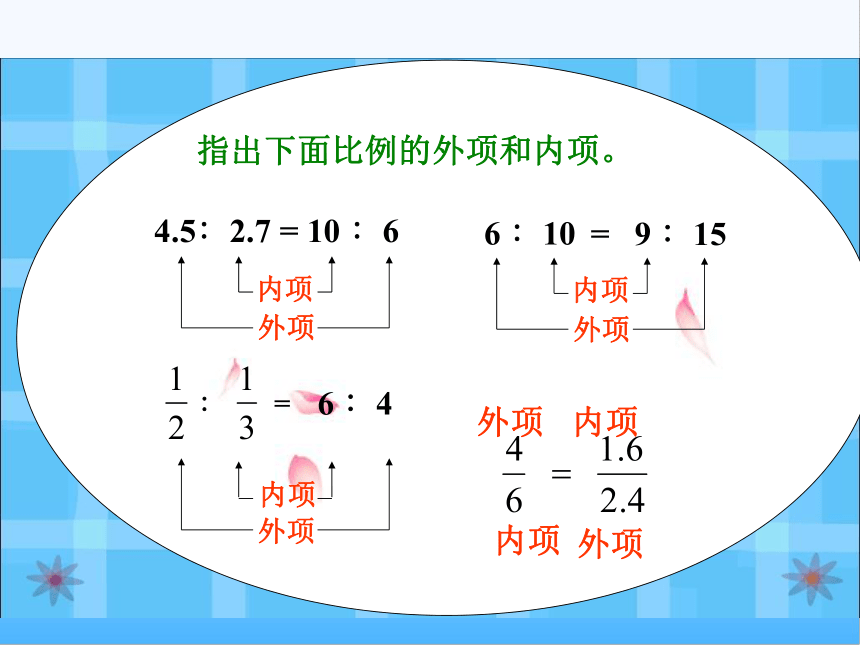
指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
∶
=
6 ∶4
外项
外项
内项
内项
外项
内项
外项
外项
内项
内项
2、计算比例中两个外项的积和两个内项的积。比较一下,你能发现什么?
例如: 2.4 ∶1.6 = 60 ∶40
外项
内项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
两个外项的积是2.4×40= ,
两个内项的积是1.6×60= ,
96
96
也就是 1.6×60 = 2.4×40
例如: 2.4 ∶1.6 = 60 ∶40
外项
内项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
两个外项的积是2.4×40= ,
两个内项的积是1.6×60= ,
96
96
也就是 1.6×60 = 2.4×40
( )
内项
( )
( )
( )
外项
外项
内项
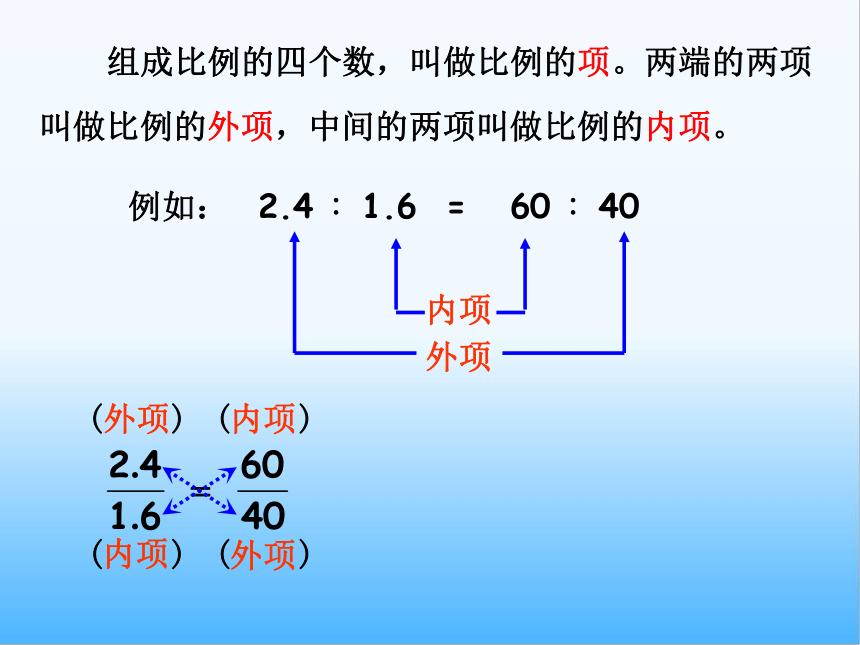
1.6×60 = 2.4×40
2.4∶1.6 = 60∶40
1.6×60 = 2.4×40
在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
3、用字母表示比例的基本性质吗?
0.5×2 =( )×( )
0.5
5
=
0.2
2
2
5
︰
1
2
=
3
5
︰
3
4
× =( )×( )
2
5
3
4
8︰25=40︰125
( )×( ) =( )×( )
试一试
5
0.2
1
2
3
5
8
125
25
40
4、 比例基本性质的用途
判断下面每组中的两个比能否组成比例?
(1) 6:15 和 8:20
根据比例的意义判断:
根据比例的基本性质判断:
判断下面每组中的两个比能否组成比例?
(2) 0.5 : 0.4 和2 : 2.5
根据比例的意义判断:
根据比例的基本性质判断:
练习1
应用比例的基本性质,判断下面哪组中的两个比
可以组成比例。
6∶3和8∶5
0.2∶2.5和4∶50
因为 6×5=30
所以 6∶3和8∶5不能
组成比例.
所以 0.2∶2.5 =4∶50
10=10
3×8=24
30≠24
因为 2.5×4=10
0.2×50=10
根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?
练习2
3×40 = 20×6
根据比例的基本性质我们知道,两个内项的积等于两个外项的积。倒过来理解,乘积相等(并且不为0)的两个乘法式子,也可以改写成比例。
根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?
3×40 = 20×6
你能把上面的等式改写成比例吗?
3:20=6:40
40:20=6:3
40:6=20:3
3:6=20:40
20:3=40:6
6:3=40:20
6:40=3:20
20:40=3:6
3和40当内项
6和20当内项
练习3
根据比例的基本性质,把下列各比改写为乘法等式。
3︰8=15︰40
=
x︰4=1︰2
9 ×0.8=1.6 ×4.5
3 ×40=8 ×15
×2=4 ×1
X
小结:
1、组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
2、在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
3、比例的基本性质可以判断两个比能否组成比例。
(一)复习旧知
1、什么叫比?比的基本性质是什么?
2.什么叫比例?
(二)自主探究。(预习41页)
1、认识比例各部分的名称。
2、比例各部分的名称和什么有关?怎样记住它们?
3、计算比例中两个外项的积和两个内项的积。比较一下,你能发现什么?
4、你能用字母表示你的发现吗?试一试。
5、比例的基本性质的用途?
复习:
1、什么叫做比?
表示两个比相等的式子叫做比例。
3、什么叫做比例?
两个数相除又叫做两个数的比。
2、什么叫比的基本性质?
比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变.
复习:
4、判断下面每组中的两个比能否组成比例?
(1) 6:15 和 8:20
根据比例的意义判断。
复习:
4、判断下面每组中的两个比能否组成比例?
(2) 0.5 : 0.4 和 2 : 2.5
根据比例的意义判断。
判断两个比能否组成比例,除了用比例的意义之外,还更简单的方法。
1、认识比例各部分的名称。
2、计算比例中两个外项的积和两个内项的积。比较一下,你能发现什么?
3、你能用字母表示你的发现吗?试一试。
4、比例的基本性质的用途?
例如: 2.4 ∶1.6 = 60 ∶40
外项
内项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
1、认识比例各部分的名称
例如: 2.4 ∶1.6 = 60 ∶40
外项
内项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
( )
内项
( )
( )
( )
外项
外项
内项
指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
∶
=
6 ∶4
外项
外项
内项
内项
外项
内项
外项
外项
内项
内项
2、计算比例中两个外项的积和两个内项的积。比较一下,你能发现什么?
例如: 2.4 ∶1.6 = 60 ∶40
外项
内项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
两个外项的积是2.4×40= ,
两个内项的积是1.6×60= ,
96
96
也就是 1.6×60 = 2.4×40
例如: 2.4 ∶1.6 = 60 ∶40
外项
内项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
两个外项的积是2.4×40= ,
两个内项的积是1.6×60= ,
96
96
也就是 1.6×60 = 2.4×40
( )
内项
( )
( )
( )
外项
外项
内项
1.6×60 = 2.4×40
2.4∶1.6 = 60∶40
1.6×60 = 2.4×40
在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
3、用字母表示比例的基本性质吗?
0.5×2 =( )×( )
0.5
5
=
0.2
2
2
5
︰
1
2
=
3
5
︰
3
4
× =( )×( )
2
5
3
4
8︰25=40︰125
( )×( ) =( )×( )
试一试
5
0.2
1
2
3
5
8
125
25
40
4、 比例基本性质的用途
判断下面每组中的两个比能否组成比例?
(1) 6:15 和 8:20
根据比例的意义判断:
根据比例的基本性质判断:
判断下面每组中的两个比能否组成比例?
(2) 0.5 : 0.4 和2 : 2.5
根据比例的意义判断:
根据比例的基本性质判断:
练习1
应用比例的基本性质,判断下面哪组中的两个比
可以组成比例。
6∶3和8∶5
0.2∶2.5和4∶50
因为 6×5=30
所以 6∶3和8∶5不能
组成比例.
所以 0.2∶2.5 =4∶50
10=10
3×8=24
30≠24
因为 2.5×4=10
0.2×50=10
根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?
练习2
3×40 = 20×6
根据比例的基本性质我们知道,两个内项的积等于两个外项的积。倒过来理解,乘积相等(并且不为0)的两个乘法式子,也可以改写成比例。
根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?
3×40 = 20×6
你能把上面的等式改写成比例吗?
3:20=6:40
40:20=6:3
40:6=20:3
3:6=20:40
20:3=40:6
6:3=40:20
6:40=3:20
20:40=3:6
3和40当内项
6和20当内项
练习3
根据比例的基本性质,把下列各比改写为乘法等式。
3︰8=15︰40
=
x︰4=1︰2
9 ×0.8=1.6 ×4.5
3 ×40=8 ×15
×2=4 ×1
X
小结:
1、组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
2、在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
3、比例的基本性质可以判断两个比能否组成比例。
