六年级数学下册课件-4.2.1 正比例 人教版(共17张PPT)
文档属性
| 名称 | 六年级数学下册课件-4.2.1 正比例 人教版(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 19:29:38 | ||
图片预览



文档简介
正 比 例
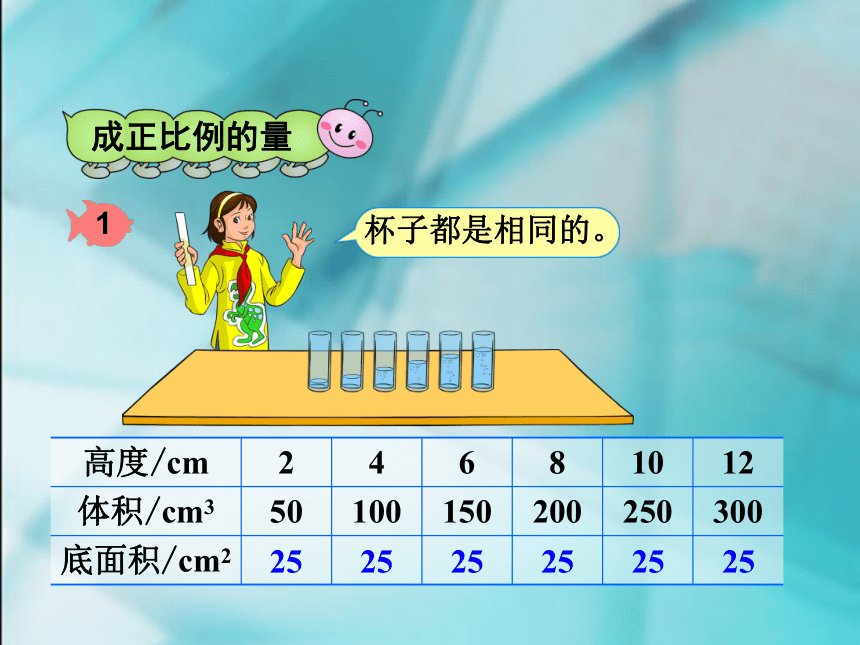
成正比例的量
杯子都是相同的。
1
高度/cm
2
4
6
8
10
12
体积/cm3
50
100
150
200
250
300
底面积/cm2
25
25
25
25
25
25
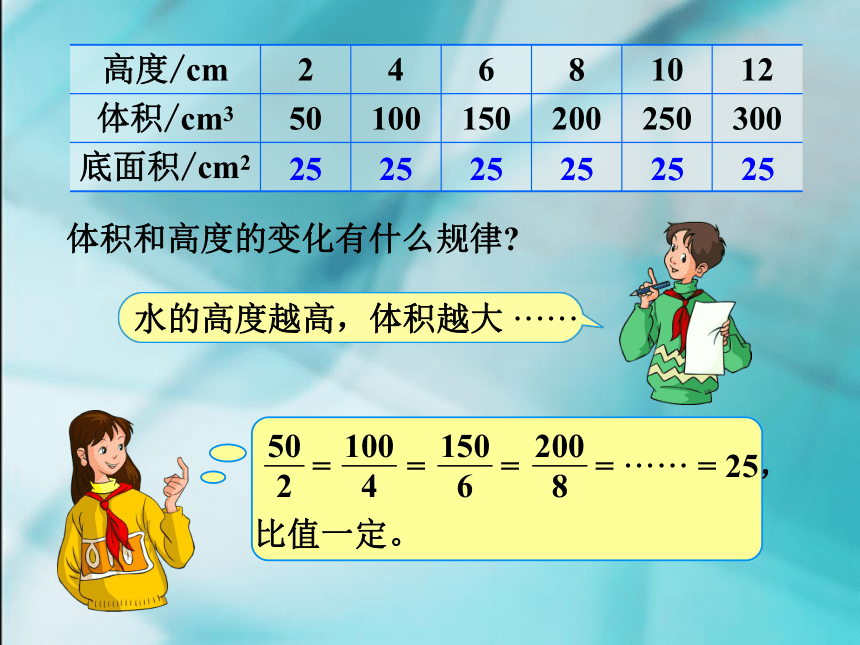
体积和高度的变化有什么规律?
水的高度越高,体积越大 ······
= = = = ······ = 25,
比值一定。
100
4
50
2
150
6
200
8
25
25
25
25
25
25
300
250
200
150
100
50
体积/cm3
底面积/cm2
12
10
8
6
4
2
高度/cm
25
25
25
25
25
25
因为杯子的底面积一定,所以水的体积随着高
度的变化而变化。水的高度增加,体积也相应增加,
水的高度降低,体积也相应减少,而且水的体积和
高度的比值一定,我们就说体积和高度成正比例关
系,体积和高度叫做成正比例的量。
如果用字母 x 和 y 表示两种相关联的量,用 k 表示它们的比值(一定),正比例关系可以用下面的式子表示:
y
x
= k (一定)
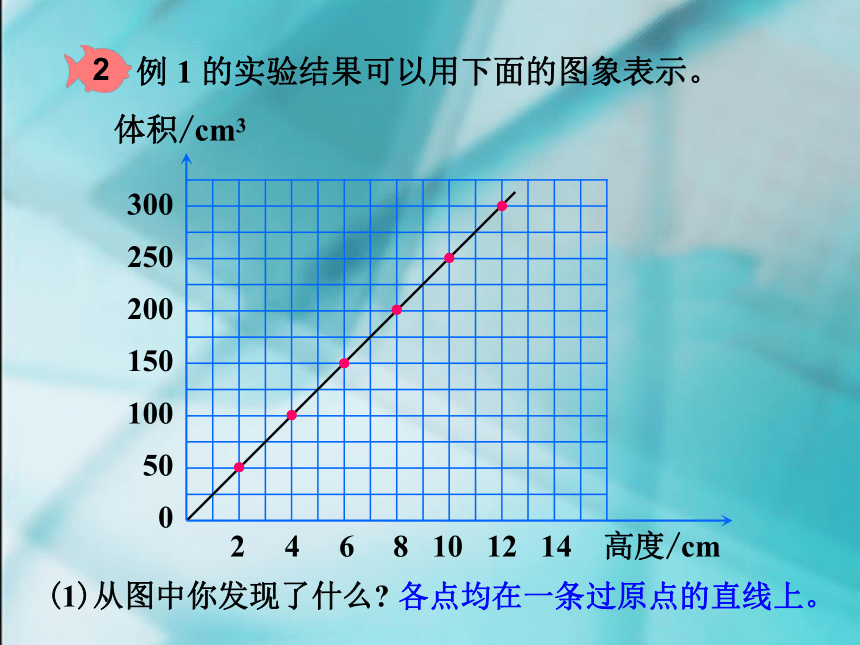
例 1 的实验结果可以用下面的图象表示。
300
250
200
150
100
50
0
2 4 6 8 10 12 14 高度/cm
(1)从图中你发现了什么?
体积/cm3
2
各点均在一条过原点的直线上。
300
250
200
150
100
50
0
2 4 6 8 10 12 14 高度/cm
体积/cm3
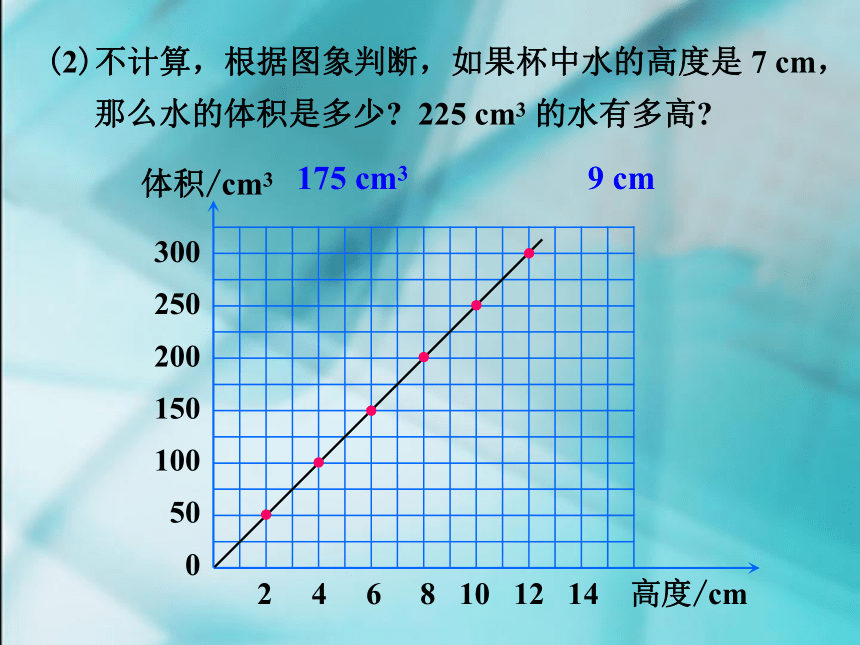
(2)不计算,根据图象判断,如果杯中水的高度是 7 cm,
那么水的体积是多少? 225 cm3 的水有多高?
175 cm3
9 cm
汽车行驶的时间和路程如下表。
时间/时
1
2
3
4
5
6
路程/km
80
160
240
320
400
480
我们开出几小时了?
行驶了多少千米?
(1) 写出几组路程和相对应的时间的比,并比较比
值的大小。说一说这个比值表示什么。
80 : 1 = 80
240 : 3 = 80
400 : 5 = 80
160 : 2 = 80
320 : 4 = 80
480 : 6 = 80
80 表示汽车行驶的速度。
时间/时
1
2
3
4
5
6
路程/km
80
160
240
320
400
480
(2) 表中的路程和时间成正比例吗?为什么?
因为 = 速度(一定),
路程
时间
所以成正比例。
时间/时
1
2
3
4
5
6
路程/km
80
160
240
320
400
480
(3)在下图中描出表示路程和相应时间的点,然后把
它们按顺序连起来。并估计一下行驶 120 km 大
约要用多长时间。
1 2 3 4 5 6 7 时间/时
480
400
320
240
160
80
0
路程/km
时间/时
1
2
3
4
5
6
路程/km
80
160
240
320
400
480
120
1.5
时间(分)
2
5
8
10
…
字数(个)
500
1250
2000
2500
…
播音员的播音时间和播音字数
成正比例吗?为什么?
播音员的播音情况如下
姚明的身高变化情况如下图:
50
60
70
80
90
100
110
120
130
140
150
160
170
出
生
时
6
个
月
1
周
岁
2
周
岁
6
周
岁
9
周
岁
身高(cm)
姚明的身高与年龄是成正比例的量吗?
52
70
85
100
150
170
(2)书的总页数一定,已经看的页数和没看
的页数。 ( )
(4)路程一定,汽车行驶的速度和时间。
( )
(3)同学们订阅《数学报》,应付的钱数
和订购的份数。( )
(1)宽一定,长方形的面积和长。( )
判断下列各题中的两种量是否成正比例,
并说明理由。
√
×
√
×
0
x
y
正比例函数
法国数学家
——笛卡儿
他用运动的观点,把变数引入了数学。建立坐标系,把“点”与“数”相对应,用方程来解决图形问题。
数学在思想方法上发生了根本的转折:由常量数学进入了变量数学的时期。
数学史上的最伟大转折点是笛卡儿的变数
成正比例的量
杯子都是相同的。
1
高度/cm
2
4
6
8
10
12
体积/cm3
50
100
150
200
250
300
底面积/cm2
25
25
25
25
25
25
体积和高度的变化有什么规律?
水的高度越高,体积越大 ······
= = = = ······ = 25,
比值一定。
100
4
50
2
150
6
200
8
25
25
25
25
25
25
300
250
200
150
100
50
体积/cm3
底面积/cm2
12
10
8
6
4
2
高度/cm
25
25
25
25
25
25
因为杯子的底面积一定,所以水的体积随着高
度的变化而变化。水的高度增加,体积也相应增加,
水的高度降低,体积也相应减少,而且水的体积和
高度的比值一定,我们就说体积和高度成正比例关
系,体积和高度叫做成正比例的量。
如果用字母 x 和 y 表示两种相关联的量,用 k 表示它们的比值(一定),正比例关系可以用下面的式子表示:
y
x
= k (一定)
例 1 的实验结果可以用下面的图象表示。
300
250
200
150
100
50
0
2 4 6 8 10 12 14 高度/cm
(1)从图中你发现了什么?
体积/cm3
2
各点均在一条过原点的直线上。
300
250
200
150
100
50
0
2 4 6 8 10 12 14 高度/cm
体积/cm3
(2)不计算,根据图象判断,如果杯中水的高度是 7 cm,
那么水的体积是多少? 225 cm3 的水有多高?
175 cm3
9 cm
汽车行驶的时间和路程如下表。
时间/时
1
2
3
4
5
6
路程/km
80
160
240
320
400
480
我们开出几小时了?
行驶了多少千米?
(1) 写出几组路程和相对应的时间的比,并比较比
值的大小。说一说这个比值表示什么。
80 : 1 = 80
240 : 3 = 80
400 : 5 = 80
160 : 2 = 80
320 : 4 = 80
480 : 6 = 80
80 表示汽车行驶的速度。
时间/时
1
2
3
4
5
6
路程/km
80
160
240
320
400
480
(2) 表中的路程和时间成正比例吗?为什么?
因为 = 速度(一定),
路程
时间
所以成正比例。
时间/时
1
2
3
4
5
6
路程/km
80
160
240
320
400
480
(3)在下图中描出表示路程和相应时间的点,然后把
它们按顺序连起来。并估计一下行驶 120 km 大
约要用多长时间。
1 2 3 4 5 6 7 时间/时
480
400
320
240
160
80
0
路程/km
时间/时
1
2
3
4
5
6
路程/km
80
160
240
320
400
480
120
1.5
时间(分)
2
5
8
10
…
字数(个)
500
1250
2000
2500
…
播音员的播音时间和播音字数
成正比例吗?为什么?
播音员的播音情况如下
姚明的身高变化情况如下图:
50
60
70
80
90
100
110
120
130
140
150
160
170
出
生
时
6
个
月
1
周
岁
2
周
岁
6
周
岁
9
周
岁
身高(cm)
姚明的身高与年龄是成正比例的量吗?
52
70
85
100
150
170
(2)书的总页数一定,已经看的页数和没看
的页数。 ( )
(4)路程一定,汽车行驶的速度和时间。
( )
(3)同学们订阅《数学报》,应付的钱数
和订购的份数。( )
(1)宽一定,长方形的面积和长。( )
判断下列各题中的两种量是否成正比例,
并说明理由。
√
×
√
×
0
x
y
正比例函数
法国数学家
——笛卡儿
他用运动的观点,把变数引入了数学。建立坐标系,把“点”与“数”相对应,用方程来解决图形问题。
数学在思想方法上发生了根本的转折:由常量数学进入了变量数学的时期。
数学史上的最伟大转折点是笛卡儿的变数
