沪教版(上海)初中数学九年级第一学期 25.1(1)锐角三角比的意义 教案
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 25.1(1)锐角三角比的意义 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 39.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 23:12:51 | ||
图片预览


文档简介
25.1(1)锐角三角比的意义
一.教学目标:
理解锐角的正切、余切的定义;经历锐角的三角比的概念的形成过程,获得从实际问题中抽象出数学概念的过程体验,培养观察、归纳、总结数学问题的能力;能正确使用锐角的正切、余切的符号语言,会利用定义求锐角的三角比的值。
二.教学重点:
锐角的正切和余切的意义。
三.教学难点:
理解一个锐角确定的直角三角形的两边的比是一个确定的值。
四、教学过程
教学环
节
教学内容
设计意图
一、
创
铺
设
垫
情
导
境
入
1.用中国2010年上海世界博览会的介绍引入。
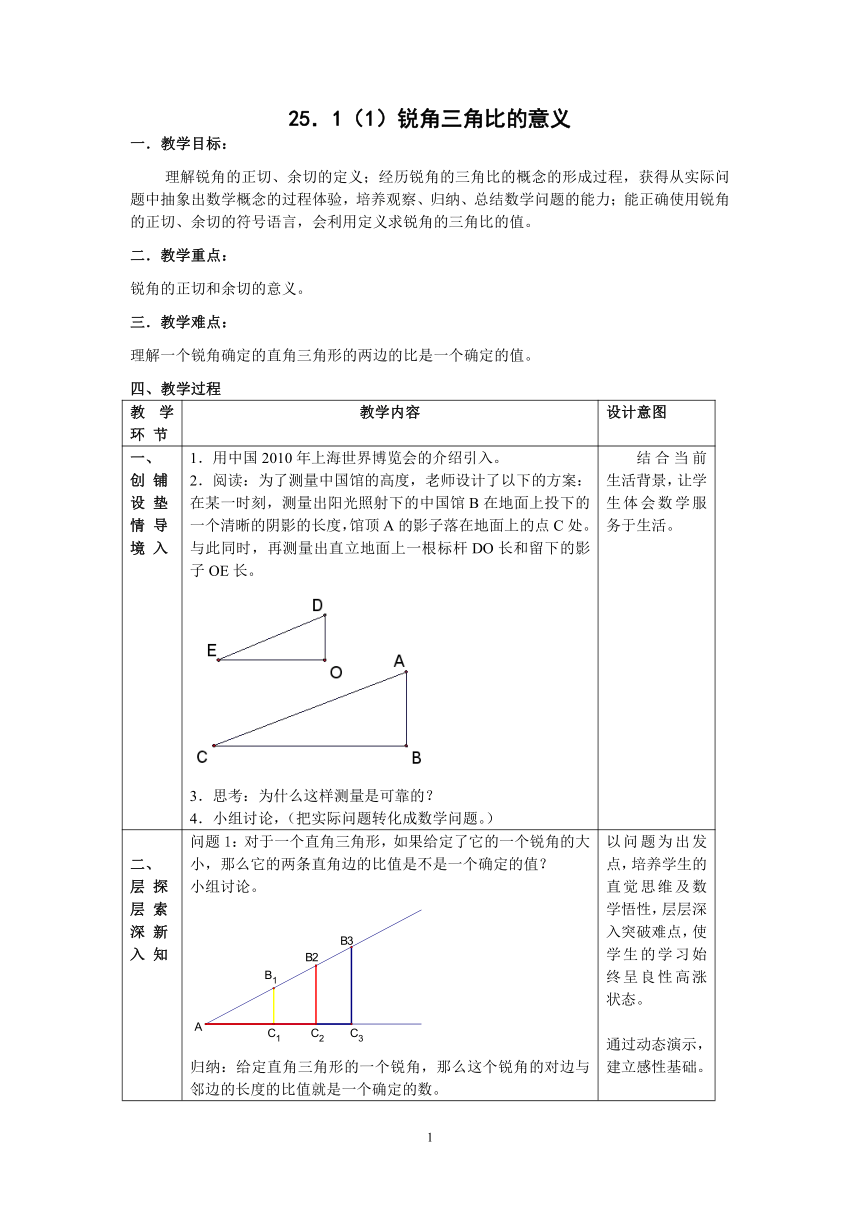
2.阅读:为了测量中国馆的高度,老师设计了以下的方案:在某一时刻,测量出阳光照射下的中国馆B在地面上投下的一个清晰的阴影的长度,馆顶A的影子落在地面上的点C处。与此同时,再测量出直立地面上一根标杆DO长和留下的影子OE长。
3.思考:为什么这样测量是可靠的?
4.小组讨论,(把实际问题转化成数学问题。)
结合当前生活背景,让学生体会数学服务于生活。
二、
层
探
层
索
深
新
入
知
问题1:对于一个直角三角形,如果给定了它的一个锐角的大小,那么它的两条直角边的比值是不是一个确定的值?
小组讨论。
归纳:给定直角三角形的一个锐角,那么这个锐角的对边与邻边的长度的比值就是一个确定的数。
问题2:当直角三角形中,一个锐角的大小变化时,这个锐角的对边与邻边的长度的比值随着变化吗?
(几何画板演示)。
归纳:直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角的大小变化而变化。
以问题为出发点,培养学生的直觉思维及数学悟性,层层深入突破难点,使学生的学习始终呈良性高涨状态。
通过动态演示,建立感性基础。
让学生认识直角三角形中一个锐角的对边与邻边的长度的比值随着这个锐角大小的变化而变化,进一步体会一个锐角的对边与邻边的长度的比值是由这个锐角的大小唯一确定的。
三、
师
研
生
究
互
新
动
知
介绍直角三角形
2.∠A的正切。
在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切.记作tanA.
板书:tanA=
3.思考:当直角三角形的一个锐角确定时,这个锐角的邻边与对边的比值确定吗?
4.∠A的余切。
在Rt△ABC中,∠C=90°,我们把锐角A的邻边与对边的比叫做∠A的余切.记作cotA.
板书:cotA=
这个环节为了方便描述,首先对直角三角形的各边进行介绍。并给出一个锐角的正切和余切的定义。
四、
练
巩
习
固
反
新
馈
知
1.简单应用:同桌间互考对方。
2.概念辨析:
①.在Rt△ABC中,tanA=。
(
)
②.在△ABC中,tanA=。(
)
③.如果直角三角形ABC的各边的长度都扩大到原来的3倍,那么锐角A的正切、余切的值也扩大原来的3倍。(
)
归纳:⑴求一个锐角的正切值,要明确在哪个直角三角形中,哪个角为直角。
(2)一个锐角的正切、余切值由角度决定,与边长无关。
例1:在Rt△ABC中,∠C=90°,AC=2,BC=3,求tanA、cotA、tanB、cotB。
想一想:cotB与tanA有什么关系?
归纳:∠A+∠B=90°,cotB=tanA;tanA=。
变式训练1:以上条件中把BC=3改成AB=3,是否还能求∠A、∠B的正切和余切。
归纳:在直角三角形中,只要知道它的两条边长,就能求出它的一个锐角的正切值和余切值。
变式训练2:过点C做CD⊥AB,垂足为D,求tan∠ACD的值。
由学生上黑板讲解思路,教师写下关键步骤。
思考:求一个角正切的方法。
归纳:求一个角的正切可以用直接法或间接法。
在练习中使学生加深对定理的理解与掌握,为例题讲解作好铺垫,体现由浅入深的原则。
本例题主要规范书写。由师生共同完成。
本题让学生比较各种方法的优劣,归纳出求一个角正切值的方法。
五、
展
总
示
结
交
新
流
知
学生自己总结,并在班上交流本节课
——
我学会了
使我感触最深的
我感到最困难的是
结合学生所述,教师给予整理。
教师与学生共同反思,把知识纳入系统,促进学生理解、提高自己的认识水平。
六、
布
分
置
层
作
落
业
实
必做题:练习册P34
习题25。1(1)
实践题:
请用量角器和刻度尺设计一个求tan27°值的方案。
(2)
请利用所学知识,测量我校新大楼的高度。
分层次布置作业,必做题促进知识的巩固,实践题供学有余力的学生完成,进一步培养学生的发散思维及社会实践能力。
教案设计说明
这是一节概念课,根据概念教学的规律和学生的认知特点,我设计了以下6个教学环节:1.创设情景,铺垫导入;2.层层深入,探究新知;3.师生互动,研究新知;4.练习反馈,巩固新知;5.展示交流,总结新知;6.布置作业,分层落实。
环节1中,以当前学生最熟悉的中国馆引出,阅读材料,让学生解释老师设计测量中国馆高度的可靠性。从相似三角形的性质得出直角三角形的两条直角边的比值是个确定的值。为下一环节的教学做好铺垫。
环节2则通过两个问题的提出让学生进行思考,得出结论:在一个直角三角形中,给定一个锐角的大小,那么它的两条直角边的比值是一个确定的值。当角度变化,比值也发生变化。并加以严格的理论证明,同时渗透函数的思想,也为后面学习“已知一个锐角的一个三角比的值求这个锐角的大小”提供依据。
环节3主要由教师介绍直角三角形的正切与余切的读法以及表示方法。为了让学生会读,会写,我设计了环节4,让同桌两位同学互相画个直角三角形,互相指出一个角的邻边、对边,及这个角的正切、余切的读法和表示方法。两个辨析题的设计为了让学生明确锐角的正切必须在直角三角形中,它的值与锐角的角度有关,与边长无关。例1是在书本的基础上加了求角A和角B的余切值。通过这道题目让学生归纳出同一个角的正切和余切的关系,互余的两个角的正切和余切的关系。并可同时得出正切、余切的取值范围。
小结与归纳是对一节课的回顾与整理,因此本节课在教师提问的基础上,让学生自己进行总结,这样可以帮助学生把所学知识纳入知识体系,形成良好的认知结构,有利于学生对知识的巩固、理解和掌握。
本节课以提高学生的数学素质为指导思想,以学生积极参与教学活动为目标,以概念讲解为载体,以展开思维分析为主线,在课堂教学中,教师充分调动一切因素,让学生在和谐、愉悦的氛围中获取知识,掌握方法。
1
一.教学目标:
理解锐角的正切、余切的定义;经历锐角的三角比的概念的形成过程,获得从实际问题中抽象出数学概念的过程体验,培养观察、归纳、总结数学问题的能力;能正确使用锐角的正切、余切的符号语言,会利用定义求锐角的三角比的值。
二.教学重点:
锐角的正切和余切的意义。
三.教学难点:
理解一个锐角确定的直角三角形的两边的比是一个确定的值。
四、教学过程
教学环
节
教学内容
设计意图
一、
创
铺
设
垫
情
导
境
入
1.用中国2010年上海世界博览会的介绍引入。
2.阅读:为了测量中国馆的高度,老师设计了以下的方案:在某一时刻,测量出阳光照射下的中国馆B在地面上投下的一个清晰的阴影的长度,馆顶A的影子落在地面上的点C处。与此同时,再测量出直立地面上一根标杆DO长和留下的影子OE长。
3.思考:为什么这样测量是可靠的?
4.小组讨论,(把实际问题转化成数学问题。)
结合当前生活背景,让学生体会数学服务于生活。
二、
层
探
层
索
深
新
入
知
问题1:对于一个直角三角形,如果给定了它的一个锐角的大小,那么它的两条直角边的比值是不是一个确定的值?
小组讨论。
归纳:给定直角三角形的一个锐角,那么这个锐角的对边与邻边的长度的比值就是一个确定的数。
问题2:当直角三角形中,一个锐角的大小变化时,这个锐角的对边与邻边的长度的比值随着变化吗?
(几何画板演示)。
归纳:直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角的大小变化而变化。
以问题为出发点,培养学生的直觉思维及数学悟性,层层深入突破难点,使学生的学习始终呈良性高涨状态。
通过动态演示,建立感性基础。
让学生认识直角三角形中一个锐角的对边与邻边的长度的比值随着这个锐角大小的变化而变化,进一步体会一个锐角的对边与邻边的长度的比值是由这个锐角的大小唯一确定的。
三、
师
研
生
究
互
新
动
知
介绍直角三角形
2.∠A的正切。
在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切.记作tanA.
板书:tanA=
3.思考:当直角三角形的一个锐角确定时,这个锐角的邻边与对边的比值确定吗?
4.∠A的余切。
在Rt△ABC中,∠C=90°,我们把锐角A的邻边与对边的比叫做∠A的余切.记作cotA.
板书:cotA=
这个环节为了方便描述,首先对直角三角形的各边进行介绍。并给出一个锐角的正切和余切的定义。
四、
练
巩
习
固
反
新
馈
知
1.简单应用:同桌间互考对方。
2.概念辨析:
①.在Rt△ABC中,tanA=。
(
)
②.在△ABC中,tanA=。(
)
③.如果直角三角形ABC的各边的长度都扩大到原来的3倍,那么锐角A的正切、余切的值也扩大原来的3倍。(
)
归纳:⑴求一个锐角的正切值,要明确在哪个直角三角形中,哪个角为直角。
(2)一个锐角的正切、余切值由角度决定,与边长无关。
例1:在Rt△ABC中,∠C=90°,AC=2,BC=3,求tanA、cotA、tanB、cotB。
想一想:cotB与tanA有什么关系?
归纳:∠A+∠B=90°,cotB=tanA;tanA=。
变式训练1:以上条件中把BC=3改成AB=3,是否还能求∠A、∠B的正切和余切。
归纳:在直角三角形中,只要知道它的两条边长,就能求出它的一个锐角的正切值和余切值。
变式训练2:过点C做CD⊥AB,垂足为D,求tan∠ACD的值。
由学生上黑板讲解思路,教师写下关键步骤。
思考:求一个角正切的方法。
归纳:求一个角的正切可以用直接法或间接法。
在练习中使学生加深对定理的理解与掌握,为例题讲解作好铺垫,体现由浅入深的原则。
本例题主要规范书写。由师生共同完成。
本题让学生比较各种方法的优劣,归纳出求一个角正切值的方法。
五、
展
总
示
结
交
新
流
知
学生自己总结,并在班上交流本节课
——
我学会了
使我感触最深的
我感到最困难的是
结合学生所述,教师给予整理。
教师与学生共同反思,把知识纳入系统,促进学生理解、提高自己的认识水平。
六、
布
分
置
层
作
落
业
实
必做题:练习册P34
习题25。1(1)
实践题:
请用量角器和刻度尺设计一个求tan27°值的方案。
(2)
请利用所学知识,测量我校新大楼的高度。
分层次布置作业,必做题促进知识的巩固,实践题供学有余力的学生完成,进一步培养学生的发散思维及社会实践能力。
教案设计说明
这是一节概念课,根据概念教学的规律和学生的认知特点,我设计了以下6个教学环节:1.创设情景,铺垫导入;2.层层深入,探究新知;3.师生互动,研究新知;4.练习反馈,巩固新知;5.展示交流,总结新知;6.布置作业,分层落实。
环节1中,以当前学生最熟悉的中国馆引出,阅读材料,让学生解释老师设计测量中国馆高度的可靠性。从相似三角形的性质得出直角三角形的两条直角边的比值是个确定的值。为下一环节的教学做好铺垫。
环节2则通过两个问题的提出让学生进行思考,得出结论:在一个直角三角形中,给定一个锐角的大小,那么它的两条直角边的比值是一个确定的值。当角度变化,比值也发生变化。并加以严格的理论证明,同时渗透函数的思想,也为后面学习“已知一个锐角的一个三角比的值求这个锐角的大小”提供依据。
环节3主要由教师介绍直角三角形的正切与余切的读法以及表示方法。为了让学生会读,会写,我设计了环节4,让同桌两位同学互相画个直角三角形,互相指出一个角的邻边、对边,及这个角的正切、余切的读法和表示方法。两个辨析题的设计为了让学生明确锐角的正切必须在直角三角形中,它的值与锐角的角度有关,与边长无关。例1是在书本的基础上加了求角A和角B的余切值。通过这道题目让学生归纳出同一个角的正切和余切的关系,互余的两个角的正切和余切的关系。并可同时得出正切、余切的取值范围。
小结与归纳是对一节课的回顾与整理,因此本节课在教师提问的基础上,让学生自己进行总结,这样可以帮助学生把所学知识纳入知识体系,形成良好的认知结构,有利于学生对知识的巩固、理解和掌握。
本节课以提高学生的数学素质为指导思想,以学生积极参与教学活动为目标,以概念讲解为载体,以展开思维分析为主线,在课堂教学中,教师充分调动一切因素,让学生在和谐、愉悦的氛围中获取知识,掌握方法。
1
