人教版九年级数学下册导学案 : 27.2.2 相似三角形的性质(含答案)
文档属性
| 名称 | 人教版九年级数学下册导学案 : 27.2.2 相似三角形的性质(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 531.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 00:00:00 | ||
图片预览

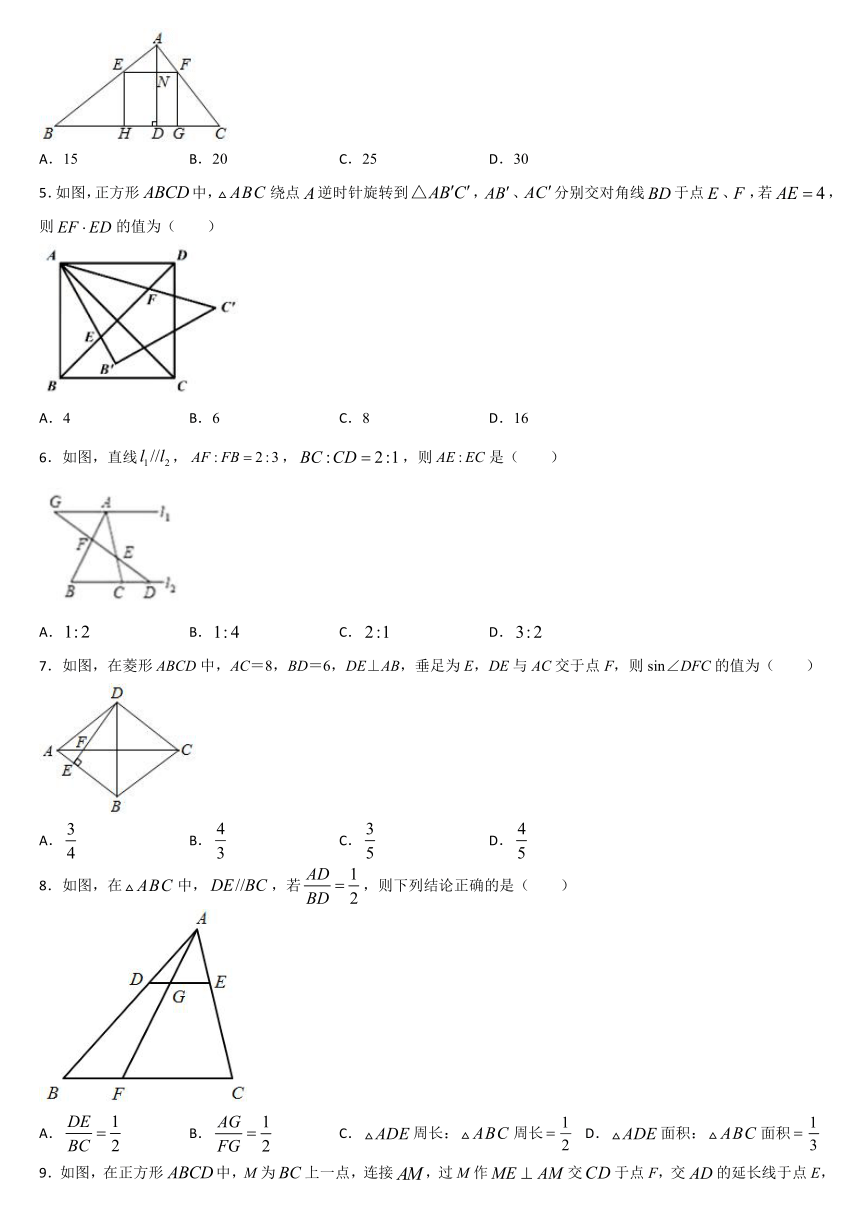


文档简介
人教版九年级数学下册导学案
第二十七章
相似
27.2.2
相似三角形的性质
【学习目标】
1.理解相似三角形的性质.
2.能运用相似三角形的性质解决简单的问题
【课前预习】
1.如图,在中,,,是的角平分线,点在上,若,,则的长为(
)
A.4
B.
C.
D.3
2.如图,在中,点E是边上的中点,G为线段上一动点,连接,交于点F,若,则的值为(
)
A.3
B.2
C.
D.
3.如图在中,其中、两点分别在、上,且,,,.若,则图中、、、的大小关系正确的是(
).
A.
B.
C.
D.
4.如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为(
)
A.15
B.20
C.25
D.30
5.如图,正方形中,绕点逆时针旋转到,、分别交对角线于点、,若,则的值为(
)
A.4
B.6
C.8
D.16
6.如图,直线,,,则是(
)
A.
B.
C.
D.
7.如图,在菱形ABCD中,AC=8,BD=6,DE⊥AB,垂足为E,DE与AC交于点F,则sin∠DFC的值为( )
A.
B.
C.
D.
8.如图,在中,,若,则下列结论正确的是(
)
A.
B.
C.周长:周长
D.面积:面积
9.如图,在正方形中,M为上一点,连接,过M作交于点F,交的延长线于点E,若,则的面积为(
)
A.3
B.4
C.8
D.9
10.如图,在中,中线,相交于点,连线,下列结论:①;②;③;④.其中正确的是(
)
A.①②③
B.②③
C.④
D.①③
【学习探究】
自主学习
阅读课本,完成下列问题
1.什么是相似三角形的相似比?
2.已知:
?ABC∽?A’B’C’,根据相似的定义,我们有哪些结论?(从对应边上看,从对应角上看)
3.思考:两个三角形相似,除了对应边成比例、对应角相等之外,我们还可以得到哪些结论?
4.如果两个三角形相似,它们的周长之间有什么关系?
如果△ABC∽△A′B′C′,且△ABC与△A′B′C′的相似比为k,即
因此AB=
,
BC=
,CA=
,
从而
=
结论:
.
同理,相似多边形的周长比等于
.
互学探究
探究一:相似三角形的性质
【小组讨论】如图,△ABC∽△A’B’C’相似比为k,尝试解决下列问题:
它们对应高、对应中线、对应角平分线的比各是多少?
(2)相似形三角形面积的比与相似比有什么关系?
(3)你能归纳出相似三角形的性质吗?
思考:相似形三角形的周长有什么关系?
练习
如图,△ABC中,D、E、F分别是边AB、BC、AC的中点,若△ABC的周长是20cm,则△DEF的周长是
(
)
A.5cm
B.10cm
C.15cm
D.20cm
探究二:相似三角形性质的运用
如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D。若△ABC的边BC上的高为6,面积为12,求
△DEF的边EF上的高和面积。
【小组讨论】
(1)△ABC和△DEF相似吗?
(2)如何运用相似三角形的性质求△DEF的边EF上的高和面积?
练习
1.如图1已知D、E分别是△ABC的AB、
AC边上的点,DE∥BC且S△ADE:S四边形DBCE=1:8,那么AE:AC等于(
)
A.1:9
B.1:3
C.1:8
D.
1:2
2.在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,如果△ABC的周长是16,面积是12,那么△DEF的周长、面积依次为(
)
A.8,3 B.8,6 C.4,3 D.4,6
如图2所示,□ABCD中,AE:EB=1:2,S△AEF=6cm2,则S△CDF=
.
【课后练习】
1.如图,在△ABC中,中线BE、CD相交于点O,连结DE,下列结论中,正确的个数有(
)
①;②;③;④.
A.1个
B.2个
C.3个
D.4个
2.如图,正方形中,点是边上一点,连接,以为对角线作正方形,边与正方形的对角线相交于点,连接.以下四个结论:
①;②;③;④.
其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
3.如图,已知四边形是矩形,把矩形沿直线折叠,点落在点处,连接.若,则的值为(
)
A.
B.
C.
D.
4.如图,中,分别在上,若,则(
)
A.
B.
C.
D.
5.如图,在中,,点D、E在边上,,若,则的面积为(
)
A.20
B.24
C.32
D.36
6.如图,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,则下列结论正确的是( )
A.∠BAE=30°
B.△ABE≌△AEF
C.CE2=AB?CF
D.CF=CD
7.若△ABC∽△DEF,它们的相似比为4:1,则△ABC与△DEF的周长比为(
)
A.2:1
B.4:1
C.8:1
D.16:1
8.如图,在中,,,的平分线交于点,交的延长线于点,若,则线段的长为(
)
A.4
B.3
C.
D.
9.如图,在△ABC中,AB=AC=5,BC=2,若点O为△ABC三条高的交点,则OA的长度为(
)
A.
B.
C.
D.
10.如图,在正方形中,点是边的中点,连接,交边于点,已知,则的长为(
)
A.1
B.
C.3
D.2
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D.
若AD=3,BD=2,则BC=_______________.
12.如图,中,如果,于点,为中点,与交于点,那么的值为______.
13.两个相似三角形的面积之差为,周长比是2:3,那么较小的三角形面积是______.
14.如图,矩形中,对角线、交于点,于点,若,,则________.
15.在矩形中,的平分线交于点E,的平分线交于点F,若,点F恰为的三等分点,则________(结果保留根号)
【参考答案】
【课前预习】
1.A
2.C
3.C
4.B
5.D
6.C
7.D
8.B
9.D
10.D
【课后练习】
1.C
2.C
3.C
4.C
5.D
6.C
7.B
8.C
9.A
10.A
11.
12.
13.
14.4.8
15.或
第二十七章
相似
27.2.2
相似三角形的性质
【学习目标】
1.理解相似三角形的性质.
2.能运用相似三角形的性质解决简单的问题
【课前预习】
1.如图,在中,,,是的角平分线,点在上,若,,则的长为(
)
A.4
B.
C.
D.3
2.如图,在中,点E是边上的中点,G为线段上一动点,连接,交于点F,若,则的值为(
)
A.3
B.2
C.
D.
3.如图在中,其中、两点分别在、上,且,,,.若,则图中、、、的大小关系正确的是(
).
A.
B.
C.
D.
4.如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,则AN的长为(
)
A.15
B.20
C.25
D.30
5.如图,正方形中,绕点逆时针旋转到,、分别交对角线于点、,若,则的值为(
)
A.4
B.6
C.8
D.16
6.如图,直线,,,则是(
)
A.
B.
C.
D.
7.如图,在菱形ABCD中,AC=8,BD=6,DE⊥AB,垂足为E,DE与AC交于点F,则sin∠DFC的值为( )
A.
B.
C.
D.
8.如图,在中,,若,则下列结论正确的是(
)
A.
B.
C.周长:周长
D.面积:面积
9.如图,在正方形中,M为上一点,连接,过M作交于点F,交的延长线于点E,若,则的面积为(
)
A.3
B.4
C.8
D.9
10.如图,在中,中线,相交于点,连线,下列结论:①;②;③;④.其中正确的是(
)
A.①②③
B.②③
C.④
D.①③
【学习探究】
自主学习
阅读课本,完成下列问题
1.什么是相似三角形的相似比?
2.已知:
?ABC∽?A’B’C’,根据相似的定义,我们有哪些结论?(从对应边上看,从对应角上看)
3.思考:两个三角形相似,除了对应边成比例、对应角相等之外,我们还可以得到哪些结论?
4.如果两个三角形相似,它们的周长之间有什么关系?
如果△ABC∽△A′B′C′,且△ABC与△A′B′C′的相似比为k,即
因此AB=
,
BC=
,CA=
,
从而
=
结论:
.
同理,相似多边形的周长比等于
.
互学探究
探究一:相似三角形的性质
【小组讨论】如图,△ABC∽△A’B’C’相似比为k,尝试解决下列问题:
它们对应高、对应中线、对应角平分线的比各是多少?
(2)相似形三角形面积的比与相似比有什么关系?
(3)你能归纳出相似三角形的性质吗?
思考:相似形三角形的周长有什么关系?
练习
如图,△ABC中,D、E、F分别是边AB、BC、AC的中点,若△ABC的周长是20cm,则△DEF的周长是
(
)
A.5cm
B.10cm
C.15cm
D.20cm
探究二:相似三角形性质的运用
如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D。若△ABC的边BC上的高为6,面积为12,求
△DEF的边EF上的高和面积。
【小组讨论】
(1)△ABC和△DEF相似吗?
(2)如何运用相似三角形的性质求△DEF的边EF上的高和面积?
练习
1.如图1已知D、E分别是△ABC的AB、
AC边上的点,DE∥BC且S△ADE:S四边形DBCE=1:8,那么AE:AC等于(
)
A.1:9
B.1:3
C.1:8
D.
1:2
2.在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,如果△ABC的周长是16,面积是12,那么△DEF的周长、面积依次为(
)
A.8,3 B.8,6 C.4,3 D.4,6
如图2所示,□ABCD中,AE:EB=1:2,S△AEF=6cm2,则S△CDF=
.
【课后练习】
1.如图,在△ABC中,中线BE、CD相交于点O,连结DE,下列结论中,正确的个数有(
)
①;②;③;④.
A.1个
B.2个
C.3个
D.4个
2.如图,正方形中,点是边上一点,连接,以为对角线作正方形,边与正方形的对角线相交于点,连接.以下四个结论:
①;②;③;④.
其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
3.如图,已知四边形是矩形,把矩形沿直线折叠,点落在点处,连接.若,则的值为(
)
A.
B.
C.
D.
4.如图,中,分别在上,若,则(
)
A.
B.
C.
D.
5.如图,在中,,点D、E在边上,,若,则的面积为(
)
A.20
B.24
C.32
D.36
6.如图,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,则下列结论正确的是( )
A.∠BAE=30°
B.△ABE≌△AEF
C.CE2=AB?CF
D.CF=CD
7.若△ABC∽△DEF,它们的相似比为4:1,则△ABC与△DEF的周长比为(
)
A.2:1
B.4:1
C.8:1
D.16:1
8.如图,在中,,,的平分线交于点,交的延长线于点,若,则线段的长为(
)
A.4
B.3
C.
D.
9.如图,在△ABC中,AB=AC=5,BC=2,若点O为△ABC三条高的交点,则OA的长度为(
)
A.
B.
C.
D.
10.如图,在正方形中,点是边的中点,连接,交边于点,已知,则的长为(
)
A.1
B.
C.3
D.2
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D.
若AD=3,BD=2,则BC=_______________.
12.如图,中,如果,于点,为中点,与交于点,那么的值为______.
13.两个相似三角形的面积之差为,周长比是2:3,那么较小的三角形面积是______.
14.如图,矩形中,对角线、交于点,于点,若,,则________.
15.在矩形中,的平分线交于点E,的平分线交于点F,若,点F恰为的三等分点,则________(结果保留根号)
【参考答案】
【课前预习】
1.A
2.C
3.C
4.B
5.D
6.C
7.D
8.B
9.D
10.D
【课后练习】
1.C
2.C
3.C
4.C
5.D
6.C
7.B
8.C
9.A
10.A
11.
12.
13.
14.4.8
15.或
