六年级数学下册课件-3.2.2 圆锥的体积人教版(共48张PPT)
文档属性
| 名称 | 六年级数学下册课件-3.2.2 圆锥的体积人教版(共48张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览








文档简介
(共48张PPT)
圆锥的体积
R·六年级下册
上节课,我们认识了圆锥,你们知道圆锥有哪些特征吗?
顶点
底面
圆锥有一个顶点。
圆锥有一个底面,底面是一个圆。
侧面
圆锥的侧面是曲面,展开后是一个扇形。
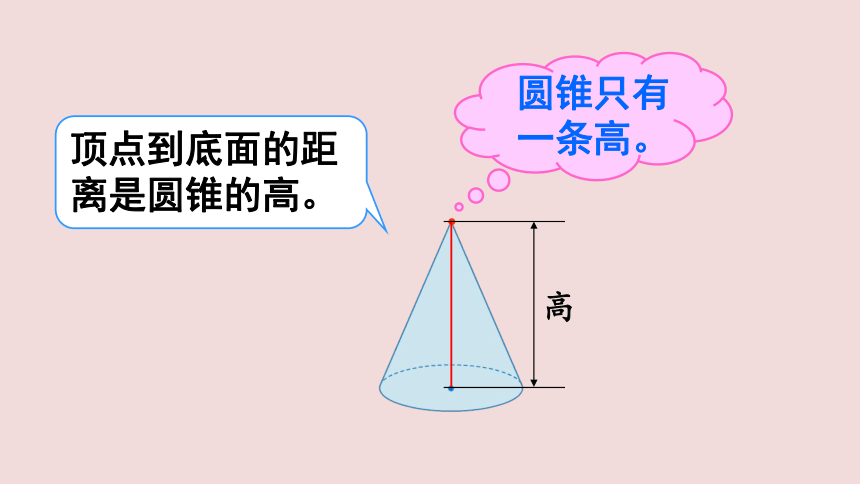
高
顶点到底面的距离是圆锥的高。
圆锥只有一条高。
圆锥底面圆周上任一点与顶点之间的距离都相等。
今天,我们来学习圆锥的体积。
回顾
圆柱体积的计算公式
V=sh
h
d
s
V=πr2h
r
V=π(
)2h
2
d
V=π(
)2h
2π
C
C
圆柱的体积=
底面积
×
高
长方体的体积=
底面积
×
高
V
=
S
h
圆柱的体积是怎么求出来的呢?
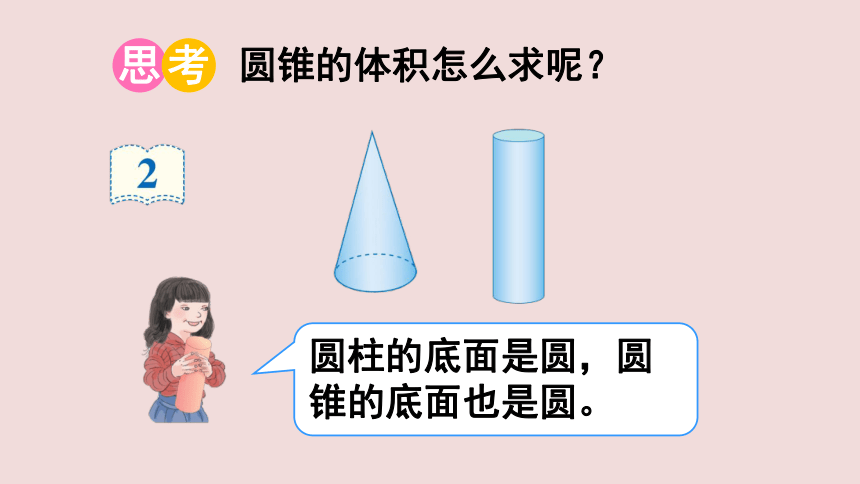
圆柱的底面是圆,圆锥的底面也是圆。
思
考
圆锥的体积怎么求呢?
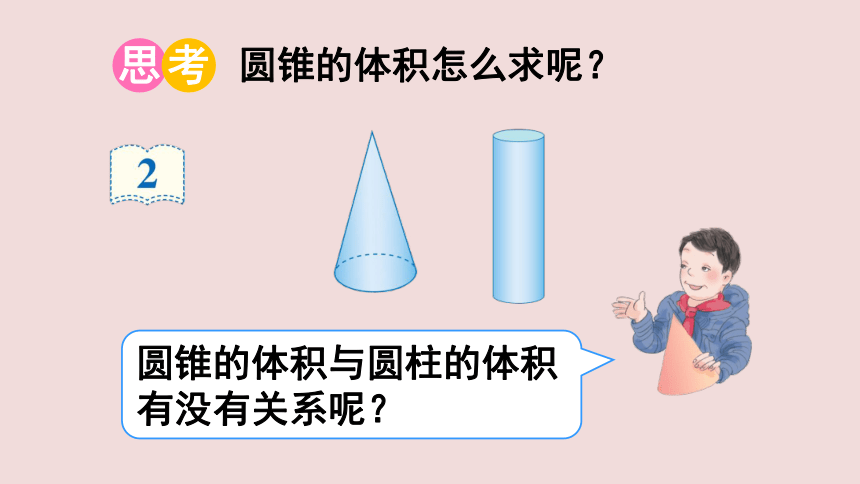
圆锥的体积与圆柱的体积有没有关系呢?
思
考
圆锥的体积怎么求呢?
圆锥的体积
下面通过试验,探究一下圆锥和圆柱体积之间的关系。
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
三次正好装满。
我把圆柱装满水,再往圆锥里倒。
正好倒了三次。
等高
等底
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
V圆锥=
V圆柱=
Sh
还有其他写法吗?
V=
sh
h
s
V=
πr2h
r
V=
π(
)2h
2
d
d
C
V=
π(
)2h
2π
C
1.
一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm?
。
×19
×12=76(cm?)
做一做
圆柱体积(cm3)
3
9
圆锥体积(cm3)
15
2.
1
45
3
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
4m
1.5m
(2)沙堆的体积:
(1)沙堆底面积:
6.28×1.5=9.42(t)
(3)沙堆重:
答:这堆沙子大约重9.42吨。
3.14
×(4÷2)2=3.14×4=12.56(m2)
×12.56×1.5=6.28(m3)
做一做
2.
一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数)
(2)铅锤的体积:
(1)铅锤底面积:
20.93×7.8≈163(g)
(3)铅锤的质量:
答:这个铅锤大约重163克
。
×12.56×5≈20.93(cm3)
3.14×(4÷2)2=3.14×4=12.56(cm2)
1.等底等高的圆柱和圆锥,圆柱的体积是12立方分米,圆锥的体积是(
)立方分米。
2.用15个同样的圆锥铝坯,可以铸造成(
)个与它等底等高的圆柱体铝坯。
4
5
3.一个圆锥和一个圆柱的体积相等,高也相等,圆柱的底面积是6cm2,圆锥的底面积是多少平方厘米?
6×3=18(平方厘米)
答:圆锥的底面积是18平方厘米。
4.一个圆锥形沙堆,底面周长是25.12米,高3米,如果每立方米沙重1.7吨,用一辆载重5吨的车来运,几次可以运完?
25.12÷3.14÷2=4(米)
3.14×42×3×
×1.7÷5≈18(次)
答:18次可以运完。
V=
sh
h
s
V=
πr2h
r
V=
π(
)2h
2
d
d
C
V=
π(
)2h
2π
C
1.完成P35第4,5,6题;
2.完成练习册本课时的习题。
圆锥的体积
R·六年级下册
上节课,我们认识了圆锥,你们知道圆锥有哪些特征吗?
顶点
底面
圆锥有一个顶点。
圆锥有一个底面,底面是一个圆。
侧面
圆锥的侧面是曲面,展开后是一个扇形。
高
顶点到底面的距离是圆锥的高。
圆锥只有一条高。
圆锥底面圆周上任一点与顶点之间的距离都相等。
今天,我们来学习圆锥的体积。
回顾
圆柱体积的计算公式
V=sh
h
d
s
V=πr2h
r
V=π(
)2h
2
d
V=π(
)2h
2π
C
C
圆柱的体积=
底面积
×
高
长方体的体积=
底面积
×
高
V
=
S
h
圆柱的体积是怎么求出来的呢?
圆柱的底面是圆,圆锥的底面也是圆。
思
考
圆锥的体积怎么求呢?
圆锥的体积与圆柱的体积有没有关系呢?
思
考
圆锥的体积怎么求呢?
圆锥的体积
下面通过试验,探究一下圆锥和圆柱体积之间的关系。
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
三次正好装满。
我把圆柱装满水,再往圆锥里倒。
正好倒了三次。
等高
等底
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
V圆锥=
V圆柱=
Sh
还有其他写法吗?
V=
sh
h
s
V=
πr2h
r
V=
π(
)2h
2
d
d
C
V=
π(
)2h
2π
C
1.
一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm?
。
×19
×12=76(cm?)
做一做
圆柱体积(cm3)
3
9
圆锥体积(cm3)
15
2.
1
45
3
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
4m
1.5m
(2)沙堆的体积:
(1)沙堆底面积:
6.28×1.5=9.42(t)
(3)沙堆重:
答:这堆沙子大约重9.42吨。
3.14
×(4÷2)2=3.14×4=12.56(m2)
×12.56×1.5=6.28(m3)
做一做
2.
一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数)
(2)铅锤的体积:
(1)铅锤底面积:
20.93×7.8≈163(g)
(3)铅锤的质量:
答:这个铅锤大约重163克
。
×12.56×5≈20.93(cm3)
3.14×(4÷2)2=3.14×4=12.56(cm2)
1.等底等高的圆柱和圆锥,圆柱的体积是12立方分米,圆锥的体积是(
)立方分米。
2.用15个同样的圆锥铝坯,可以铸造成(
)个与它等底等高的圆柱体铝坯。
4
5
3.一个圆锥和一个圆柱的体积相等,高也相等,圆柱的底面积是6cm2,圆锥的底面积是多少平方厘米?
6×3=18(平方厘米)
答:圆锥的底面积是18平方厘米。
4.一个圆锥形沙堆,底面周长是25.12米,高3米,如果每立方米沙重1.7吨,用一辆载重5吨的车来运,几次可以运完?
25.12÷3.14÷2=4(米)
3.14×42×3×
×1.7÷5≈18(次)
答:18次可以运完。
V=
sh
h
s
V=
πr2h
r
V=
π(
)2h
2
d
d
C
V=
π(
)2h
2π
C
1.完成P35第4,5,6题;
2.完成练习册本课时的习题。
