六年级数学下册课件-3.2.2 圆锥的体积人教版(共118张PPT)
文档属性
| 名称 | 六年级数学下册课件-3.2.2 圆锥的体积人教版(共118张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 19:47:02 | ||
图片预览






文档简介
(共118张PPT)
圆锥的体积
人教版六年级数学下册
教材分析:
本节课属于空间与图形知识的教学,是小学阶段几何知识的重难点部分,是小学学习立体图形体积计算的飞跃,通过这部分知识的教学,可以发展学生的空间观念、想象能力,较深入地理解几何体体积推导方法的新领域,为学生进一步学习几何知识奠定良好的基础。本节内容是在学生了解了圆锥的特征,掌握了圆柱体积的计算方法基础上进行教学的,教材重视类比,转化思想的渗透,直观引导学生经历“猜测、类比、观察、实验、探究、推理、总结”的探索过程,理解掌握求圆锥体积的计算公式,会运用公式计算圆锥的体积。这样不仅帮助学生建立空间观念,还能培养学生抽象的逻辑思维能力,激发学生的想象力.
教学目标:
1、知识与技能:掌握圆锥的体积计算公式,能运用公式求圆锥的体积,并且能运用这一知识解决生活中一些简单的实际问题。
2、过程与方法:通过“直觉猜想——试验探索——合作交流——得出结论——实践运用”探索过程,获得圆锥体积的推导过程和学习的方法。
3、情感、态度与价值观:培养学生勇于探索的求知精神,感受到数学来源于生活,能积极参与数学活动,自觉养成与人合作交流与独立思考的良好习惯。
教学重点:圆锥体积公式的理解,并能运用公式求圆锥的体积。
教学难点:圆锥体积公式的推
学具准备:等底等高的圆柱和圆锥、水、小桶、实验记录表、多媒体课件
复习:
圆柱的体积计算公式:
圆柱体积
=
底面积
×
高
V柱
=
Sh
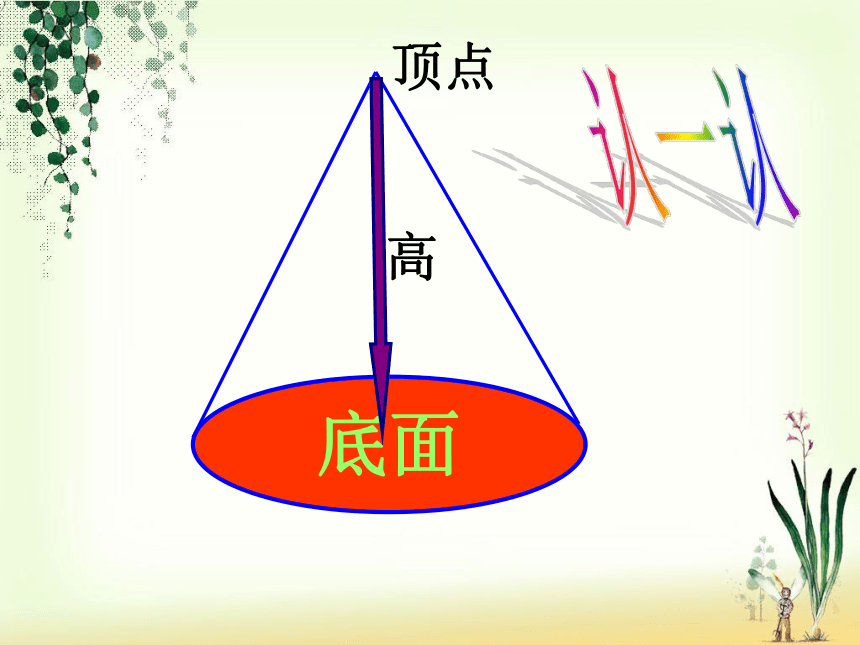
底面
顶点
高
圆柱和圆锥的底和高有
什么关系?
圆柱和圆锥等底等高
想一想:
猜想:等底等高的圆柱和圆锥的体积有什么关系呢?谁的体积更大些?
圆柱的体积是与它等底等高圆锥体积的3倍。
圆柱体积=底面积
高
圆柱体积=底面积
高
圆柱体积=底面积
高
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
底面积
高
圆柱体积=底面积
高
1
3
圆锥体积=
底面积
高
圆柱体积=底面积
高
1
3
圆锥体积=
底面积
高
想一想,讨论一下:
(1)通过刚才的实验,你发现了什么?
(2)要求圆锥的体积必须知道什么?
等底等高时,圆锥体积是圆柱体积的三分之一
底面积和高
例题1:学以致用
一个圆锥的零件,底面半径是3厘米,高是18厘米。这个零件的体积是多少?
V锥=
=3.14×3×3×18×
=169.56(立方厘米)
答:这个零件的体积是169.56立方厘米。
Sh
例2、在打谷场上,有一个近似于圆锥的小麦堆,测得底面直径是4米,高是1.2米。每立方米小麦约重700千克,这堆小麦约有多少千克?
1.2米
4米
r=4÷2=2(米)
V锥=
=3.14×2×2×1.2×
=5.024(立方米)
5.024×700=3516.8(千克)
答:这堆小麦约有3516.8千克
Sh
例3、一个体积为30立方厘米的圆锥形的零件,底面积是18平方厘米,这个零件的高是多少?
答:这个零件的高是5立方厘米。
Sh
根据:V
=
30
=
×18×h
h=5(厘米)
一、填空:
1.
圆锥的体积=(
),用字母表示是(
)。
2.
圆柱体积的
与和它(
)的圆锥的体积相等。
3.
一个圆柱和一个圆锥等底等高,圆柱的体积是3立方分米,圆锥的体积是(
)立方分米。
4.
一个圆锥的底面积是12平方厘米,高是6厘米,体积是(
)立方厘米。
等底等高
1
24
×底面积×高
V=
s
h
二、判断:
1.
圆柱体的体积一定比圆锥体的体积大(
)
2.
圆锥的体积等于和它等底等高的圆柱体的
(
)
3.
正方体、长方体、圆锥体的体积都等于底面积×高。
(
)
4.
等底等高的圆柱和圆锥,如果圆柱体的体积是27立方米,那么圆锥的体积是9立方米。(
)
√
×
√
×
三、填表:
已
知
条
件
体积
圆锥底面半径2厘米,高9厘米
圆锥底面直径6厘米,高3厘米
圆锥底面周长6.28分米,高6分米
37.68立方厘米
28.26立方厘米
6.28立方分米
有一根底面直径是6厘米,长是15厘米的圆柱形钢材,要把它削成与它等底等高的圆锥形零件。要削去钢材多少立方厘米?
15厘米
6厘米
总结:
今天有什么收获?
你学会了什么?
圆锥的体积=底面积×高×1/3
V锥=S×h×1/3
圆锥的体积
人教版六年级数学下册
教材分析:
本节课属于空间与图形知识的教学,是小学阶段几何知识的重难点部分,是小学学习立体图形体积计算的飞跃,通过这部分知识的教学,可以发展学生的空间观念、想象能力,较深入地理解几何体体积推导方法的新领域,为学生进一步学习几何知识奠定良好的基础。本节内容是在学生了解了圆锥的特征,掌握了圆柱体积的计算方法基础上进行教学的,教材重视类比,转化思想的渗透,直观引导学生经历“猜测、类比、观察、实验、探究、推理、总结”的探索过程,理解掌握求圆锥体积的计算公式,会运用公式计算圆锥的体积。这样不仅帮助学生建立空间观念,还能培养学生抽象的逻辑思维能力,激发学生的想象力.
教学目标:
1、知识与技能:掌握圆锥的体积计算公式,能运用公式求圆锥的体积,并且能运用这一知识解决生活中一些简单的实际问题。
2、过程与方法:通过“直觉猜想——试验探索——合作交流——得出结论——实践运用”探索过程,获得圆锥体积的推导过程和学习的方法。
3、情感、态度与价值观:培养学生勇于探索的求知精神,感受到数学来源于生活,能积极参与数学活动,自觉养成与人合作交流与独立思考的良好习惯。
教学重点:圆锥体积公式的理解,并能运用公式求圆锥的体积。
教学难点:圆锥体积公式的推
学具准备:等底等高的圆柱和圆锥、水、小桶、实验记录表、多媒体课件
复习:
圆柱的体积计算公式:
圆柱体积
=
底面积
×
高
V柱
=
Sh
底面
顶点
高
圆柱和圆锥的底和高有
什么关系?
圆柱和圆锥等底等高
想一想:
猜想:等底等高的圆柱和圆锥的体积有什么关系呢?谁的体积更大些?
圆柱的体积是与它等底等高圆锥体积的3倍。
圆柱体积=底面积
高
圆柱体积=底面积
高
圆柱体积=底面积
高
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
圆柱体积=底面积
高
圆锥体积=
底面积
高
圆柱体积=底面积
高
1
3
圆锥体积=
底面积
高
圆柱体积=底面积
高
1
3
圆锥体积=
底面积
高
想一想,讨论一下:
(1)通过刚才的实验,你发现了什么?
(2)要求圆锥的体积必须知道什么?
等底等高时,圆锥体积是圆柱体积的三分之一
底面积和高
例题1:学以致用
一个圆锥的零件,底面半径是3厘米,高是18厘米。这个零件的体积是多少?
V锥=
=3.14×3×3×18×
=169.56(立方厘米)
答:这个零件的体积是169.56立方厘米。
Sh
例2、在打谷场上,有一个近似于圆锥的小麦堆,测得底面直径是4米,高是1.2米。每立方米小麦约重700千克,这堆小麦约有多少千克?
1.2米
4米
r=4÷2=2(米)
V锥=
=3.14×2×2×1.2×
=5.024(立方米)
5.024×700=3516.8(千克)
答:这堆小麦约有3516.8千克
Sh
例3、一个体积为30立方厘米的圆锥形的零件,底面积是18平方厘米,这个零件的高是多少?
答:这个零件的高是5立方厘米。
Sh
根据:V
=
30
=
×18×h
h=5(厘米)
一、填空:
1.
圆锥的体积=(
),用字母表示是(
)。
2.
圆柱体积的
与和它(
)的圆锥的体积相等。
3.
一个圆柱和一个圆锥等底等高,圆柱的体积是3立方分米,圆锥的体积是(
)立方分米。
4.
一个圆锥的底面积是12平方厘米,高是6厘米,体积是(
)立方厘米。
等底等高
1
24
×底面积×高
V=
s
h
二、判断:
1.
圆柱体的体积一定比圆锥体的体积大(
)
2.
圆锥的体积等于和它等底等高的圆柱体的
(
)
3.
正方体、长方体、圆锥体的体积都等于底面积×高。
(
)
4.
等底等高的圆柱和圆锥,如果圆柱体的体积是27立方米,那么圆锥的体积是9立方米。(
)
√
×
√
×
三、填表:
已
知
条
件
体积
圆锥底面半径2厘米,高9厘米
圆锥底面直径6厘米,高3厘米
圆锥底面周长6.28分米,高6分米
37.68立方厘米
28.26立方厘米
6.28立方分米
有一根底面直径是6厘米,长是15厘米的圆柱形钢材,要把它削成与它等底等高的圆锥形零件。要削去钢材多少立方厘米?
15厘米
6厘米
总结:
今天有什么收获?
你学会了什么?
圆锥的体积=底面积×高×1/3
V锥=S×h×1/3
