苏科版九年级数学期末复习教案:圆与线段比例
文档属性
| 名称 | 苏科版九年级数学期末复习教案:圆与线段比例 |  | |
| 格式 | zip | ||
| 文件大小 | 161.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 23:10:25 | ||
图片预览


文档简介
教学内容
圆与比例线段
教学目标
掌握相似的灵魂-比例
重点
利用相似三角形解决实际问题
难点
灵活运用比例
教学过程
知识解读:
比例线段在求线段的长度,证明线段等积式、线段相等、两直线平行,线段倍分关系等方面有广泛的应用;
由相似三角形得对应边成比例,是研究比例线段的最重要方法,而角在圆中转化灵活,为寻找构造相似三角形、得到比例线段提供可能性
当直线形与圆结合时,就产生错综复杂的图形,善于分析图形是解与圆相关综合题的关键,分析图形可从以下方面入手
多视点观察图形
多元素分析图形。图中有没有特殊点,特殊线,特殊三角形,特殊四边形,全等三角形,相似三角形
将以上分析组合,寻找练习
例题精讲
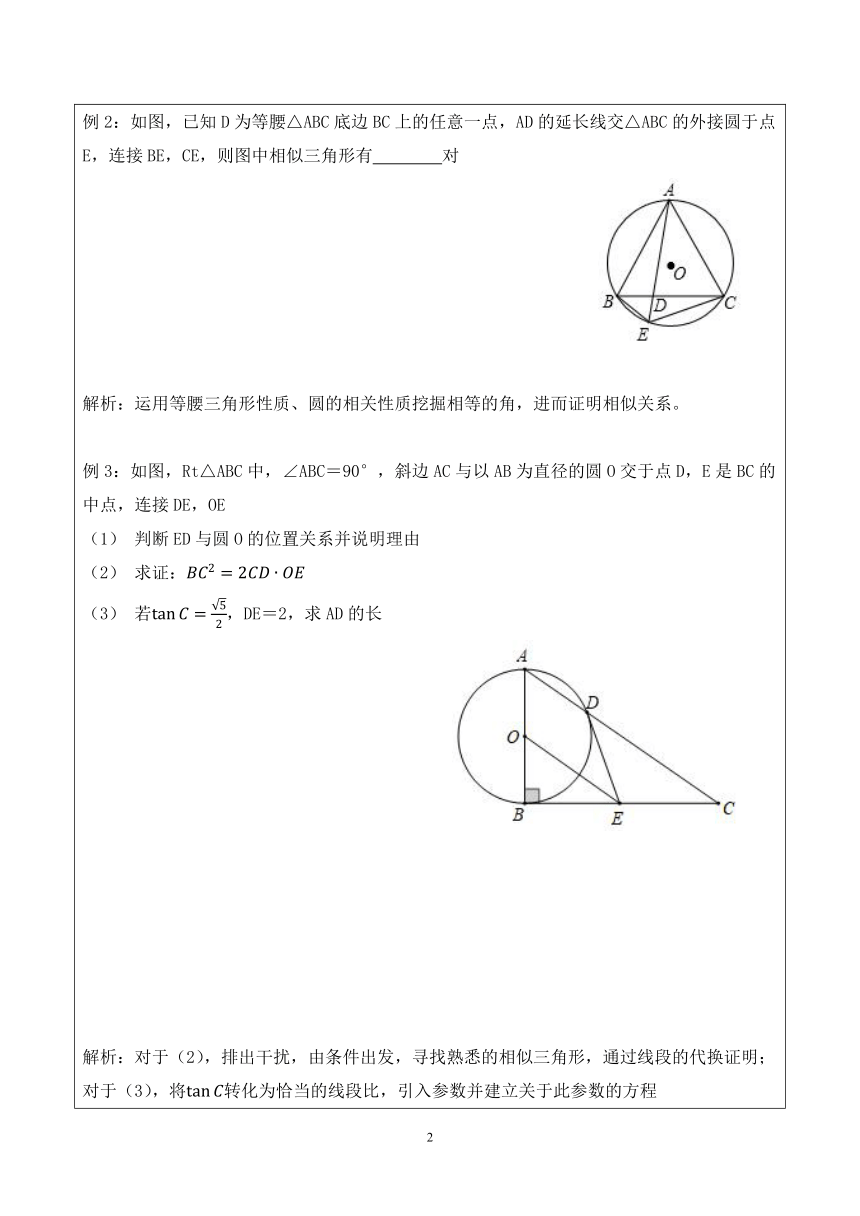
例1:如图,AB是半圆的直径,AC是一条弦,D是AC弧的中点,DE⊥AB于点E,且DE交AC于点F,DB交AC于点G,若EF∶AE=3∶4,则CG∶GB=
;
试一试:添加与直径相关的辅助线,寻找与CG,GB所在三角形的相似三角形
例2:如图,已知D为等腰△ABC底边BC上的任意一点,AD的延长线交△ABC的外接圆于点E,连接BE,CE,则图中相似三角形有
对
解析:运用等腰三角形性质、圆的相关性质挖掘相等的角,进而证明相似关系。
例3:如图,Rt△ABC中,∠ABC=90°,斜边AC与以AB为直径的圆O交于点D,E是BC的中点,连接DE,OE
判断ED与圆O的位置关系并说明理由
求证:
若,DE=2,求AD的长
解析:对于(2),排出干扰,由条件出发,寻找熟悉的相似三角形,通过线段的代换证明;对于(3),将转化为恰当的线段比,引入参数并建立关于此参数的方程
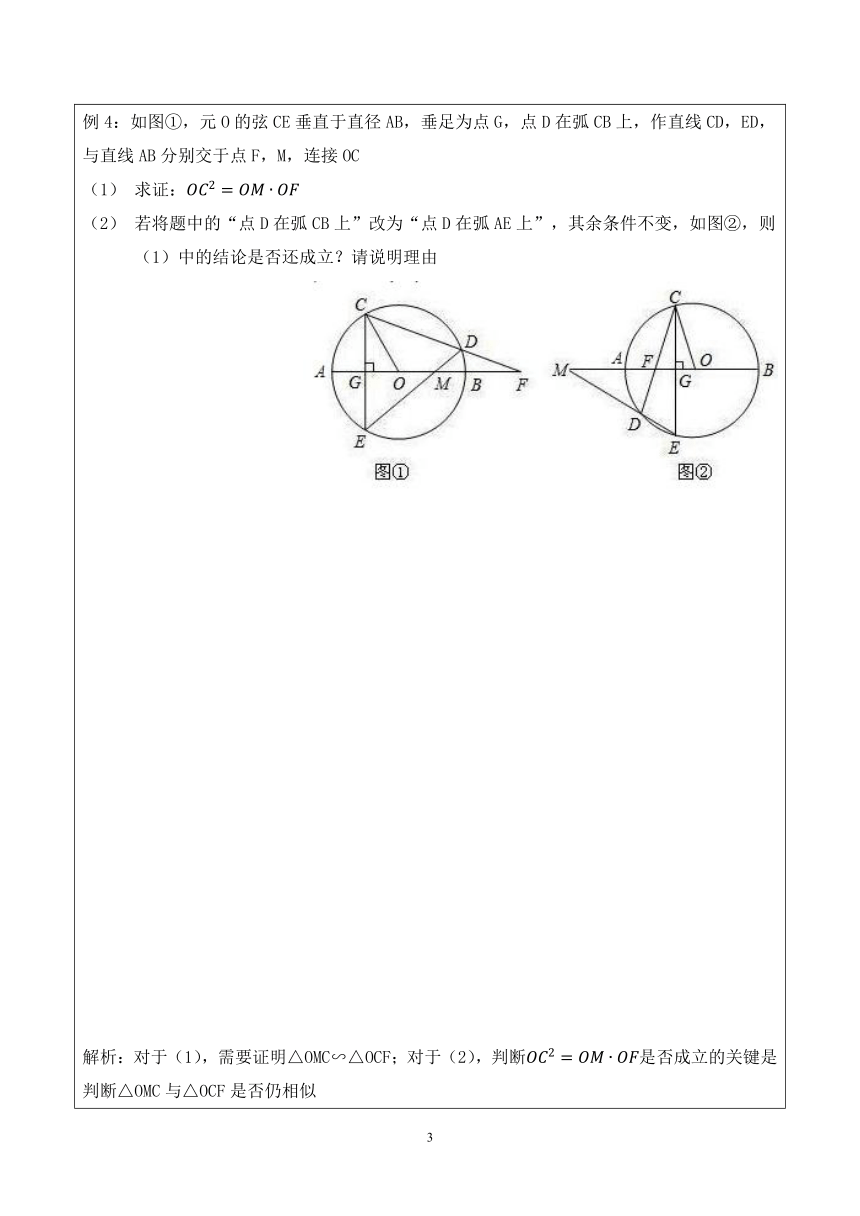
例4:如图①,元O的弦CE垂直于直径AB,垂足为点G,点D在弧CB上,作直线CD,ED,与直线AB分别交于点F,M,连接OC
求证:
若将题中的“点D在弧CB上”改为“点D在弧AE上”,其余条件不变,如图②,则(1)中的结论是否还成立?请说明理由
解析:对于(1),需要证明△OMC∽△OCF;对于(2),判断是否成立的关键是判断△OMC与△OCF是否仍相似
例5:如图,AB是圆O直径,弦CD⊥AB于点H,过CD延长线上一点E作圆O的切线交AB的延长线于点F,切线为点G,连接AG交CD于点K
求证:KE=GE
若,试判断AC与EF的位置关系,并说明理由
在(2)的条件下,若,AK=,求FG的长
解析:(1)(2)是(3)的基础,为条件的转化运用创造条件
例6:如图,已知四边形ABCD为任意一个圆内接四边形,求证:AB·CD+AD·BC=AC·BD
托勒密定理:
托勒密是古希腊天文学家、数学家。约在公元150年,他写出天文学巨著《天文学大成》。在天文学的推动下,托勒密提出如下命题:圆内接四边形两组对边乘积的和等于两条对角线的乘积。史称“托勒密定理”
解析:将问题转化为比例线段的证明,为此需构造相似三角形
综合练习:
练习1:如图,已知圆O是△ABC的外接圆,BC是圆O的直径,D是劣弧AC的中点,BD交AC于点E,若BC=,CD=,则DE=
练习2:如图,已知△ABC内接于圆O,且AB=AC,直径AD交BC于点E,F是OE的中点,如果BD∥CF,BC=,则CD=
练习3:如图,△ABC内接于圆O,AH⊥BC于点H,若AC=24,AH=18,圆O的半径OC=13,则AB=
练习4:如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的圆O与AD相切,点E为AD的中点,下列结论中:①AB+CD=AD;②;③AB·CD=;④∠ABE=∠DCE。其中正确的有
练习5:如图,AB是圆O的直径,点P在BA的延长线上,PD与圆O相切于点D,过点B作PD的垂线交PD的延长线于点C,若圆O的半径为4,BC=6,则PA=
练习6:如图,在以AB为直径的半圆中,有一内接正方形CDEF,其边长为1,若AC=a,BC=b,则下列关系中不正确的是(
)
A.
a-b=1
B.
ab=1
C.
a+b=
D.
练习7:如图,△ABC内接于圆O,且∠ABC=∠C,点D在弧BC上运动,过点D作DE∥BC,DE交直线AB于点E,连接BD;
求证:∠ADB=∠E
求证:
当点D运动到什么位置时,△DBE∽△ADE
练习8:已知圆O上有两个定点A,B和两个动点C,D,AC与BD交于点E
如图1,求证:EA·EC=EB·ED
如图2,若弧AB等于弧BC,AD是圆O的直径,求证AD·AC=2BD·BC
如图3,若AC⊥BD,点O到AD的距离为2,求BC的长
练习9:如图,AB为圆O的直径,P点为半径OA上异于O点和A点的一个点,过P点作直线AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE,DE,AE交CD于F点
求证:DE为圆O的切线
若圆O的半径为3,,求AD的长
请猜想PF与FD的数量关系,并加以证明
练习10:如图,△ABC是圆O的内接三角形,点D在弧BC上,点E在弦AB上(点E不与点A重合),且四边形BDCE为菱形
求证:AC=CE
求证
已知圆O的半径为3
①若AB∶AC=5∶3,求BC的长
②当AB∶AC为何值时,AB·AC的值最大
(
9
)
圆与比例线段
教学目标
掌握相似的灵魂-比例
重点
利用相似三角形解决实际问题
难点
灵活运用比例
教学过程
知识解读:
比例线段在求线段的长度,证明线段等积式、线段相等、两直线平行,线段倍分关系等方面有广泛的应用;
由相似三角形得对应边成比例,是研究比例线段的最重要方法,而角在圆中转化灵活,为寻找构造相似三角形、得到比例线段提供可能性
当直线形与圆结合时,就产生错综复杂的图形,善于分析图形是解与圆相关综合题的关键,分析图形可从以下方面入手
多视点观察图形
多元素分析图形。图中有没有特殊点,特殊线,特殊三角形,特殊四边形,全等三角形,相似三角形
将以上分析组合,寻找练习
例题精讲
例1:如图,AB是半圆的直径,AC是一条弦,D是AC弧的中点,DE⊥AB于点E,且DE交AC于点F,DB交AC于点G,若EF∶AE=3∶4,则CG∶GB=
;
试一试:添加与直径相关的辅助线,寻找与CG,GB所在三角形的相似三角形
例2:如图,已知D为等腰△ABC底边BC上的任意一点,AD的延长线交△ABC的外接圆于点E,连接BE,CE,则图中相似三角形有
对
解析:运用等腰三角形性质、圆的相关性质挖掘相等的角,进而证明相似关系。
例3:如图,Rt△ABC中,∠ABC=90°,斜边AC与以AB为直径的圆O交于点D,E是BC的中点,连接DE,OE
判断ED与圆O的位置关系并说明理由
求证:
若,DE=2,求AD的长
解析:对于(2),排出干扰,由条件出发,寻找熟悉的相似三角形,通过线段的代换证明;对于(3),将转化为恰当的线段比,引入参数并建立关于此参数的方程
例4:如图①,元O的弦CE垂直于直径AB,垂足为点G,点D在弧CB上,作直线CD,ED,与直线AB分别交于点F,M,连接OC
求证:
若将题中的“点D在弧CB上”改为“点D在弧AE上”,其余条件不变,如图②,则(1)中的结论是否还成立?请说明理由
解析:对于(1),需要证明△OMC∽△OCF;对于(2),判断是否成立的关键是判断△OMC与△OCF是否仍相似
例5:如图,AB是圆O直径,弦CD⊥AB于点H,过CD延长线上一点E作圆O的切线交AB的延长线于点F,切线为点G,连接AG交CD于点K
求证:KE=GE
若,试判断AC与EF的位置关系,并说明理由
在(2)的条件下,若,AK=,求FG的长
解析:(1)(2)是(3)的基础,为条件的转化运用创造条件
例6:如图,已知四边形ABCD为任意一个圆内接四边形,求证:AB·CD+AD·BC=AC·BD
托勒密定理:
托勒密是古希腊天文学家、数学家。约在公元150年,他写出天文学巨著《天文学大成》。在天文学的推动下,托勒密提出如下命题:圆内接四边形两组对边乘积的和等于两条对角线的乘积。史称“托勒密定理”
解析:将问题转化为比例线段的证明,为此需构造相似三角形
综合练习:
练习1:如图,已知圆O是△ABC的外接圆,BC是圆O的直径,D是劣弧AC的中点,BD交AC于点E,若BC=,CD=,则DE=
练习2:如图,已知△ABC内接于圆O,且AB=AC,直径AD交BC于点E,F是OE的中点,如果BD∥CF,BC=,则CD=
练习3:如图,△ABC内接于圆O,AH⊥BC于点H,若AC=24,AH=18,圆O的半径OC=13,则AB=
练习4:如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的圆O与AD相切,点E为AD的中点,下列结论中:①AB+CD=AD;②;③AB·CD=;④∠ABE=∠DCE。其中正确的有
练习5:如图,AB是圆O的直径,点P在BA的延长线上,PD与圆O相切于点D,过点B作PD的垂线交PD的延长线于点C,若圆O的半径为4,BC=6,则PA=
练习6:如图,在以AB为直径的半圆中,有一内接正方形CDEF,其边长为1,若AC=a,BC=b,则下列关系中不正确的是(
)
A.
a-b=1
B.
ab=1
C.
a+b=
D.
练习7:如图,△ABC内接于圆O,且∠ABC=∠C,点D在弧BC上运动,过点D作DE∥BC,DE交直线AB于点E,连接BD;
求证:∠ADB=∠E
求证:
当点D运动到什么位置时,△DBE∽△ADE
练习8:已知圆O上有两个定点A,B和两个动点C,D,AC与BD交于点E
如图1,求证:EA·EC=EB·ED
如图2,若弧AB等于弧BC,AD是圆O的直径,求证AD·AC=2BD·BC
如图3,若AC⊥BD,点O到AD的距离为2,求BC的长
练习9:如图,AB为圆O的直径,P点为半径OA上异于O点和A点的一个点,过P点作直线AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE,DE,AE交CD于F点
求证:DE为圆O的切线
若圆O的半径为3,,求AD的长
请猜想PF与FD的数量关系,并加以证明
练习10:如图,△ABC是圆O的内接三角形,点D在弧BC上,点E在弦AB上(点E不与点A重合),且四边形BDCE为菱形
求证:AC=CE
求证
已知圆O的半径为3
①若AB∶AC=5∶3,求BC的长
②当AB∶AC为何值时,AB·AC的值最大
(
9
)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
