人教版八年级数学上册全册培优资料(Word版 无答案)
文档属性
| 名称 | 人教版八年级数学上册全册培优资料(Word版 无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 12.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 00:00:00 | ||
图片预览


文档简介
第01讲 全等三角形的性质与判定
考点·方法·破译
1.能够完全重合的两个三角形叫全等三角形.全等三角形的形状和大小完全相同;
2.全等三角形性质:①全等三角形对应边相等,对应角相等;②全等三角形对应高、角平分线、中线相等;③全等三角形对应周长相等,面积相等;
3.全等三角形判定方法有:SAS,ASA,AAS,SSS,对于两个直角三角形全等的判定方法,除上述方法外,还有HL法;
4.证明两个三角形全等的关键,就是证明两个三角形满足判定方法中的三个条件,具体分析步骤是先找出两个三角形中相等的边或角,再根据选定的判定方法,确定还需要证明哪些相等的边或角,再设法对它们进行证明;
5..证明两个三角形全等,根据条件,有时能直接进行证明,有时要证的两个三角形并不全等,这时需要添加辅助线构造全等三角形,构造全等三角形常用的方法有:平移、翻折、旋转、等倍延长线中线、截取等等.
经典·考题·赏析
【例1】如图,AB∥EF∥DC,∠ABC=90°,AB=CD,那么图中有全等三角形( )
A.5对 B.4对 C.3对 D.2对
【解法指导】从题设题设条件出发,首先找到比较明显的一对全等三角形,并由此推出结论作为下面有用的条件,从而推出第二对,第三对全等三角形.这种逐步推进的方法常用到.
解:⑴∵AB∥EF∥DC,∠ABC=90. ∴∠DCB=90.
在△ABC和△DCB中
∴△ABC≌∴△DCB(SAS ) ∴∠A=∠D
⑵在△ABE和△DCE中
∴△ABE≌∴△DCE ∴BE=CE
⑶在Rt△EFB和Rt△EFC中
∴Rt△EFB≌Rt△EFC(HL)故选C.
【变式题组】
01.(天津)下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
02.(丽水)已知命题:如图,点A、D、B、E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.
03.(上海)已知线段AC与BD相交于点O, 连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).
⑴添加条件∠A=∠D,∠OEF=∠OFE,求证:AB=DC;
⑵分别将“∠A=∠D”记为①,“∠OEF=∠OFE”记为②,“AB=DC”记为③,添加①、③,以②为结论构成命题1;添加条件②、③,以①为结论构成命题2.命题1是______命题,命题2是_______命题(选择“真”或“假”填入空格).
【例2】已知AB=DC,AE=DF,CF=FB. 求证:AF=DE.
【解法指导】想证AF=DE,首先要找出AF和DE所在的三角形.AF在△AFB和△AEF中,而DE在△CDE和△DEF中,因而只需证明△ABF≌△DCE或△AEF≌△DFE即可.然后再根据已知条件找出证明它们全等的条件.
证明:∵FB=CE ∴FB+EF=CE+EF,即BE=CF
在△ABE和△DCF中,
∴△ABE≌△DCF(SSS) ∴∠B=∠C
在△ABF和△DCE中, ∴△ABF≌△DCE ∴AF=DE
【变式题组】
01.如图,AD、BE是锐角△ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为( )
A.2 B.3 C.4 D.5
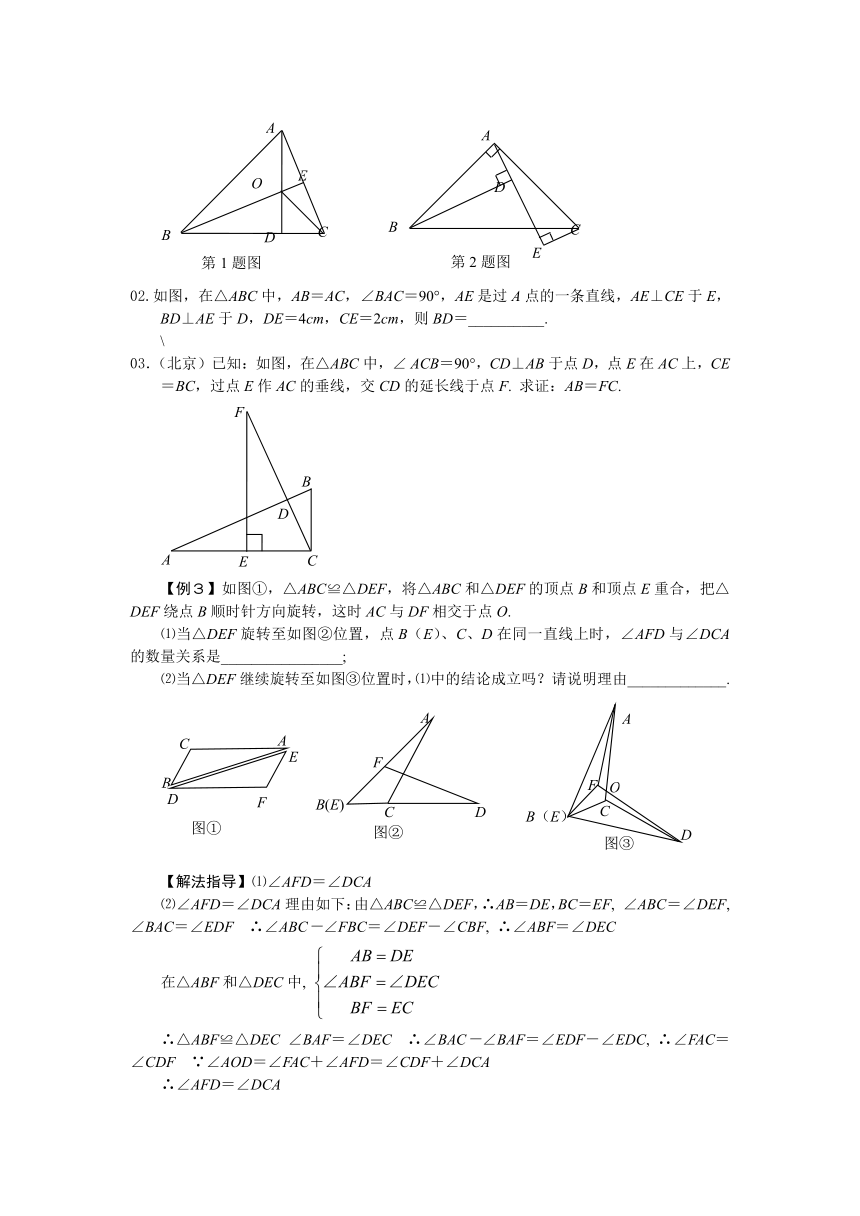
02.如图,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,AE⊥CE于E,BD⊥AE于D,DE=4cm,CE=2cm,则BD=__________.
\
03.(北京)已知:如图,在△ABC中,∠ ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过点E作AC的垂线,交CD的延长线于点F. 求证:AB=FC.
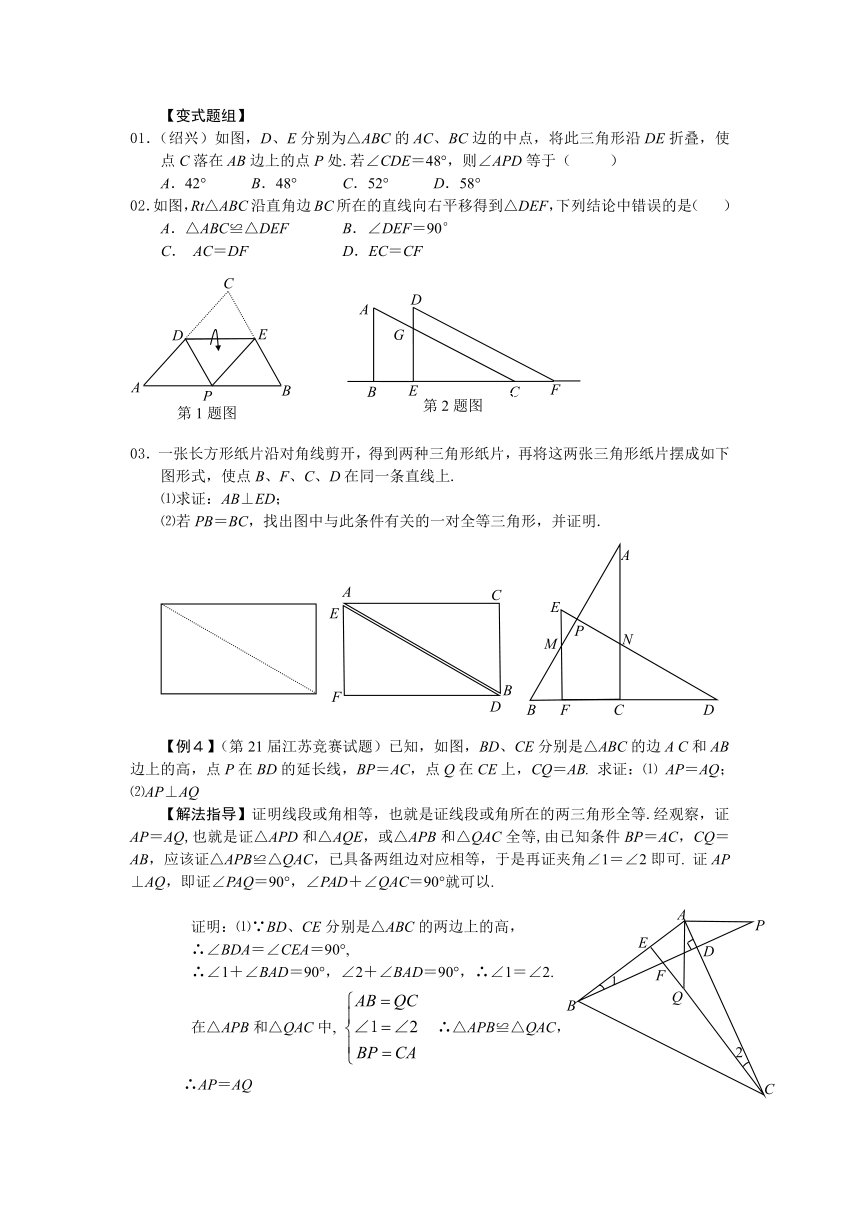
【例3】如图①,△ABC≌△DEF,将△ABC和△DEF的顶点B和顶点E重合,把△DEF绕点B顺时针方向旋转,这时AC与DF相交于点O.
⑴当△DEF旋转至如图②位置,点B(E)、C、D在同一直线上时,∠AFD与∠DCA的数量关系是________________;
⑵当△DEF继续旋转至如图③位置时,⑴中的结论成立吗?请说明理由_____________.
【解法指导】⑴∠AFD=∠DCA
⑵∠AFD=∠DCA理由如下:由△ABC≌△DEF,∴AB=DE,BC=EF, ∠ABC=∠DEF, ∠BAC=∠EDF ∴∠ABC-∠FBC=∠DEF-∠CBF, ∴∠ABF=∠DEC
在△ABF和△DEC中,
∴△ABF≌△DEC ∠BAF=∠DEC ∴∠BAC-∠BAF=∠EDF-∠EDC, ∴∠FAC=∠CDF ∵∠AOD=∠FAC+∠AFD=∠CDF+∠DCA
∴∠AFD=∠DCA
【变式题组】
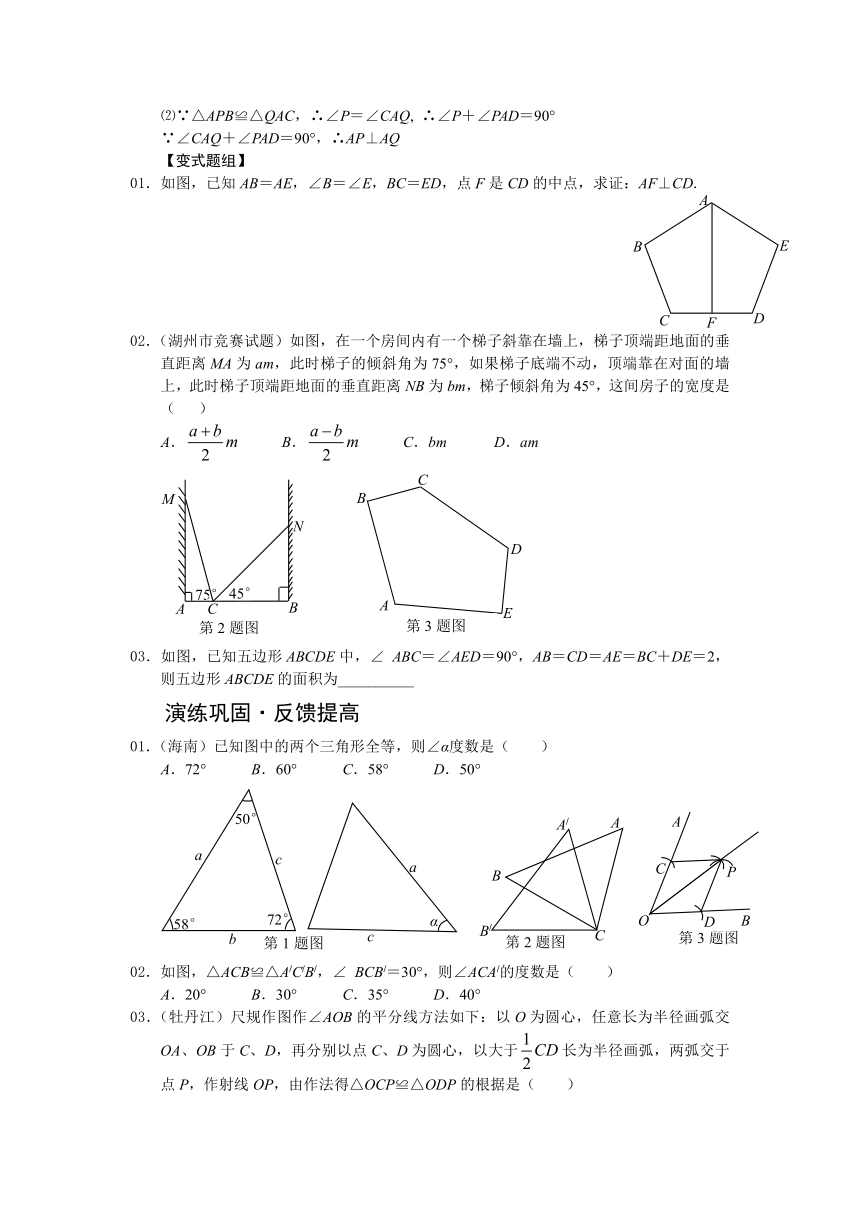
01.(绍兴)如图,D、E分别为△ABC的AC、BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )
A.42° B.48° C.52° D.58°
02.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( )
A.△ABC≌△DEF B.∠DEF=90°
C. AC=DF D.EC=CF
03.一张长方形纸片沿对角线剪开,得到两种三角形纸片,再将这两张三角形纸片摆成如下图形式,使点B、F、C、D在同一条直线上.
⑴求证:AB⊥ED;
⑵若PB=BC,找出图中与此条件有关的一对全等三角形,并证明.
【例4】(第21届江苏竞赛试题)已知,如图,BD、CE分别是△ABC的边A C和AB边上的高,点P在BD的延长线,BP=AC,点Q在CE上,CQ=AB. 求证:⑴ AP=AQ;⑵AP⊥AQ
【解法指导】证明线段或角相等,也就是证线段或角所在的两三角形全等.经观察,证AP=AQ,也就是证△APD和△AQE,或△APB和△QAC全等,由已知条件BP=AC,CQ=AB,应该证△APB≌△QAC,已具备两组边对应相等,于是再证夹角∠1=∠2即可. 证AP⊥AQ,即证∠PAQ=90°,∠PAD+∠QAC=90°就可以.
证明:⑴∵BD、CE分别是△ABC的两边上的高,
∴∠BDA=∠CEA=90°,
∴∠1+∠BAD=90°,∠2+∠BAD=90°,∴∠1=∠2.
在△APB和△QAC中, ∴△APB≌△QAC,
∴AP=AQ
⑵∵△APB≌△QAC,∴∠P=∠CAQ, ∴∠P+∠PAD=90°
∵∠CAQ+∠PAD=90°,∴AP⊥AQ
【变式题组】
01.如图,已知AB=AE,∠B=∠E,BC=ED,点F是CD的中点,求证:AF⊥CD.
02.(湖州市竞赛试题)如图,在一个房间内有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为am,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子顶端距地面的垂直距离NB为bm,梯子倾斜角为45°,这间房子的宽度是( )
A. B. C.bm D.am
03.如图,已知五边形ABCDE中,∠ ABC=∠AED=90°,AB=CD=AE=BC+DE=2,则五边形ABCDE的面积为__________
演练巩固·反馈提高
01.(海南)已知图中的两个三角形全等,则∠α度数是( )
A.72° B.60° C.58° D.50°
02.如图,△ACB≌△A/C/B/,∠ BCB/=30°,则∠ACA/的度数是( )
A.20° B.30° C.35° D.40°
03.(牡丹江)尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA、OB于C、D,再分别以点C、D为圆心,以大于长为半径画弧,两弧交于点P,作射线OP,由作法得△OCP≌△ODP的根据是( )
A.SAS B.ASA C.AAS D.SSS
04.(江西)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A. CB=CD B.∠BAC=∠DAC
C. ∠BCA=∠DCA D.∠B=∠D=90°
05.有两块不同大小的等腰直角三角板△ABC和△BDE,将它们的一个锐角顶点放在一起,将它们的一个锐角顶点放在一起,如图,当A、B、D不在一条直线上时,下面的结论不正确的是( )
A. △ABE≌△CBD B. ∠ABE=∠CBD
C. ∠ABC=∠EBD=45° D. AC∥BE
06.如图,△ABC和共顶点A,AB=AE,∠1=∠2,∠B=∠E. BC交AD于M,DE交AC于N,小华说:“一定有△ABC≌△AED.”小明说:“△ABM≌△AEN.”那么( )
A. 小华、小明都对 B. 小华、小明都不对
C. 小华对、小明不对 D.小华不对、小明对
07.如图,已知AC=EC, BC=CD, AB=ED,如果∠BCA=119°,∠ACD=98°,那么∠ECA的度数是___________.
08.如图,△ABC≌△ADE,BC延长线交DE于F,∠B=25°,∠ACB=105°,∠DAC=10°,则∠DFB的度数为_______.
09.如图,在Rt△ABC中,∠C=90°, DE⊥AB于D, BC=BD. AC=3,那么AE+DE=______
10.如图,BA⊥AC, CD∥AB. BC=DE,且BC⊥DE,若AB=2, CD=6,则AE=_____.
11.如图, AB=CD, AB∥CD. BC=12cm,同时有P、Q两只蚂蚁从点C出发,沿CB方向爬行,P的速度是0.1cm/s, Q的速度是0.2cm/s. 求爬行时间t为多少时,△APB≌△QDC.
12.如图, △ABC中,∠BCA=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
⑴求证:AE=CD;
⑵若AC=12cm, 求BD的长.
13.(吉林)如图,AB=AC,AD⊥BC于点D,AD等于AE,AB平分∠DAE交DE于点F, 请你写出图中三对全等三角形,并选取其中一对加以证明.
14.如图,将等腰直角三角板ABC的直角顶点C放在直线l上,从另两个顶点A、B分别作l的垂线,垂足分别为D、E.
⑴找出图中的全等三角形,并加以证明;
⑵若DE=a,求梯形DABE的面积.(温馨提示:补形法)
15.如图,AC⊥BC, AD⊥BD, AD=BC,CE⊥AB,DF⊥AB,垂足分别是E、F.求证:CE=DF.
16.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,那么在什么情况下,它们会全等?
⑴阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等;
对于这两个三角形均为钝角三角形,可证明它们全等(证明略);
对于这两个三角形均为锐角三角形,它们也全等,可证明如下;
已知△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.求证:△ABC≌△A1B1C1.(请你将下列证明过程补充完整)
⑵归纳与叙述:由⑴可得一个正确结论,请你写出这个结论.
培优升级·奥赛检测
01.如图,在△ABC中,AB=AC,E、F分别是AB、AC上的点,且AE=AF,BF、CE相交于点O,连接AO并延长交BC于点D,则图中全等三角形有( )
A.4对 B.5对 C.6对 D.7对
02.如图,在△ABC中,AB=AC,OC=OD,下列结论中:①∠A=∠B ②DE=CE,③连接DE, 则OE平分∠AOB,正确的是( )
A.①② B.②③ C.①③ D.①②③
03.如图,A在DE上,F在AB上,且AC=CE , ∠1=∠2=∠3, 则DE的长等于()
A.DC B. BC C. AB D.AE+AC
04.下面有四个命题,其中真命题是( )
A.两个三角形有两边及一角对应相等,这两个三角形全等
B.两边和第三边上的高对应相等的两个三角形全等
C. 有一角和一边对应相等的两个直角三角形全等
D. 两边和第三边上的中线对应相等的两个三角形全等
05.在△ABC中,高AD和BE所在直线相交于H点,且BH=AC,则∠ABC=_______.
06.如图,EB交AC于点M, 交FC于点D, AB交FC于点N,∠E=∠F=90°,∠B=∠C, AE=AF. 给出下列结论:①∠1=∠2;②BE=CF; ③△ACN≌△ABM; ④CD=DB,其中正确的结论有___________.(填序号)
07.如图,AD为在△ABC的高,E为AC上一点,BE交AD于点F,且有BF=AC,FD=CD.
⑴求证:BE⊥AC;
⑵若把条件“BF=AC”和结论“BE⊥AC”互换,这个命题成立吗?证明你的判定.
08.如图,D为在△ABC的边BC上一点,且CD=AB,∠BDA=∠BAD,AE是△ABD的中线.求证:AC=2AE.
09.如图,在凸四边形ABCD中,E为△ACD内一点,满足AC=AD,AB=AE, ∠BAE+∠BCE=90°, ∠BAC=∠EAD.求证:∠CED=90°.
10.(沈阳)将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
⑴求证:AF+EF=DE;
⑵若将图①中△DBE绕点B顺时针方向旋转角α,且0°<α<60°,其他条件不变,请在图②中画出变换后的图形,并直接写出(1)中结论是否仍然成立;
⑶若将图①中△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其他条件不变,如图③你认为(1)中结论还成立吗?若成立,写出证明过程;若不成立,请写出此时AF、EF与DE之间的关系,并说明理由。
11.(嵊州市高中提前招生考试)⑴阅读理解:课外兴趣小组活动时,老师提出了如下问题:在△ABC中,AB=5,AC=13, 求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑中线加倍,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
⑵问题解决:受到⑴的启发,请你证明下面命题:如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
求证:BE+CF>EF;
⑶问题拓展:如图,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
12.(北京)如图,已知△ABC.
⑴请你在BC边上分别取两点D、E(BC的中点除外),连接AD、AE,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
⑵请你根据使⑴成立的相应条件,证明:AB+AC>AD+AE.
13.如图,AB=AD,AC=AE,∠BAD=∠CAE=180°. AH⊥AH于H,HA的延长线交DE于G. 求证:GD=GE.
14.已知,四边形ABCD中,AB⊥AD,BC⊥CD,BA=BC,∠ABC=120°,∠MBN=60°, ∠MBN绕B点旋转,它的两边分别交AD、DC(或它们的延长线)于E、F.
当∠MBN绕B点旋转到AE=CF时,如图1,易证:AE+CF=EF;(不需证明)
当∠MBN绕B点旋转到AE≠CF时,如图2和图3中这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请写出你的猜想,不需证明.
第02讲 角平分线的性质与判定
考点·方法·破译
1.角平分线的性质定理:角平分线上的点到角两边的距离相等.
2.角平分线的判定定理:角的内角到角两边距离相等的点在这个角的平分线上.
3.有角平分线时常常通过下列几种情况构造全等三角形.
经典·考题·赏析
【例1】如图,已知OD平分∠AOB,在OA、OB边上截取OA=OB,PM⊥BD,PN⊥AD.求证:PM=PN
【解法指导】由于PM⊥BD,PN⊥AD.欲证PM=PN只需∠3=∠4,证∠3=∠4,只需∠3和∠4所在的△OBD与△OAD全等即可.
证明:∵OD平分∠AOB ∴∠1=∠2
在△OBD与△OAD中, ∴△OBD≌△OAD
∴∠3=∠4 ∵PM⊥BD,PN⊥AD 所以PM=PN
【变式题组】
01.如图,CP、BP分别平分△ABC的外角∠BCM、∠CBN.求证:点P在∠BAC的平分线上.
02.如图,BD平分∠ABC,AB=BC,点P是BD延长线上的一点,PM⊥AD,PN⊥CD.求证:PM=PN
【例2】(天津竞赛题)如图,已知四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且AE=(AB+AD),如果∠D=120°,求∠B的度数
【解法指导】由已知∠1=∠2,CE⊥AB,联想到可作CF⊥AD于F,得CE=CF,AF=AE,又由AE=(AB+AD)得DF=EB,于是可证△CFD≌△CEB,则∠B=∠CDF=60°.或者在AE上截取AM=AD从而构造全等三角形.
解:过点C作CF⊥AD于点F.∵AC平分∠BAD,CE⊥AB,点C是AC上一点,
∴CE=CF
在Rt△CFA和Rt△CEA中, ∴Rt△ACF≌Rt△ACE ∴AF=AE
又∵AE=(AE+BE+AF-DF),2AE=AE+AF+BE-DF,∴BE=DF
∵CF⊥AD,CE⊥AB,∴∠F=∠CEB=90°
在△CEB和△CFD中,,∴△CEB≌△CFD
∴∠B=∠CDF 又∵∠ADC=120°,∴∠CDF=60°,即∠B=60°.
【变式题组】
01.如图,在△ABC中,CD平分∠ACB,AC=5,BC=3.求
02.(河北竞赛)在四边形ABCD中,已知AB=a,AD=b.且BC=DC,对角线AC平分∠BAD,问a与b的大小符合什么条件时,有∠B+∠D=180°,请画图并证明你的结论.
【例3】如图,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,CE⊥BE.求证:CE=BD
【解法指导】由于BE平分∠ABC,因而可以考虑过点D作BC的垂线或延长CE从而构造全等三角形.
证明:延长CE交BA的延长线于F,∵∠1=∠2,BE=BE,∠BEF=∠BEC
∴△BEF≌△BEC(ASA) ∴CE=EF,∴CE=CF ∵∠1+∠F=∠3+∠F=90°,
∴∠1=∠3
在△ABD和△ACF中,,∴△ABD≌△ACF
∴BD=CF ∴CE=BD
【变式题组】
01.如图,已知AC∥BD,EA、EB分别平分∠CAB、∠DBA,CD过点E,求证:AB=AC+BD.
02.如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
⑴请你判断FE和FD之间的数量关系,并说明理由;
⑵求证:AE+CD=AC.
演练巩固·反馈提高
01.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于D,若CD=n,AB=m,则△ABD的面积是( )
A.mn B.mn C. mn D.2 mn
02.如图,已知AB=AC,BE=CE,下面四个结论:①BP=CP;②AD⊥BC;③AE平分∠BAC;④∠PBC=∠PCB.其中正确的结论个数有( )个
A. 1 B.2 C.3 D.4
03.如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S.若AQ=PQ,PR=PS,下列结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是( )
A. ①③ B.②③ C.①② D.①②③
04.如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD上任意一点到AB、AC的距离相等;③AD⊥BC且BD=CD;④∠BDE=∠CDF.其中正确的是( )
A.②③ B.②④ C.②③④ D.①②③④
05.如图,在Rt△ABC中,∠ACB=90°,∠CAB=30°,∠ACB的平分线与∠ABC的外角平分线交于E点,则∠AEB的度数为( )
A.50° B.45° C.40° D.35°
06.如图,P是△ABC内一点,PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,且PD=PE=PF,给出下列结论:①AD=AF;②AB+EC=AC+BE;③BC+CF=AB+AF;④点P是△ABC三条角平分线的交点.其中正确的序号是( )
A.①②③④ B.①②③ C.①②④ D.②③④
07.如图,点P是△ABC两个外角平分线的交点,则下列说法中不正确的是( )
A.点P到△ABC三边的距离相等 B.点P在∠ABC的平分线上
C.∠P与∠B的关系是:∠P+∠B=90° D.∠P与∠B的关系是:∠B=∠P
08.如图,BD平分∠ABC,CD平分∠ACE,BD与CD相交于D.给出下列结论:①点D到AB、AC的距离相等;②∠BAC=2∠BDC;③DA=DC;④DB平分∠ADC.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
09.如图,△ABC中,∠C=90°AD是△ABC的角平分线,DE⊥AB于E,下列结论中:①AD平分∠CDE;②∠BAC=∠BDE;③ DE平分∠ADB;④AB=AC+BE.其中正确的个数有( )
A.3个 B.2个 C.1个 D.4个
10.如图,已知BQ是∠ABC的内角平分线,CQ是∠ACB的外角平分线,由Q出发,作点Q到BC、AC和AB的垂线QM、QN和QK,垂足分别为M、N、K,则QM、QN、QK的关系是_________
11.如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC.求证:BE=CF
12.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F.求证:AD⊥EF.
培优升级·奥赛检测
01.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有( )
A.一处 B.二处 C.三处 D.四处
02.已知Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD:CD=9:7,则D到AB边的距离为( )
A.18 B.16 C.14 D.12
03.如图,△ABC中,∠C=90°,AD是△ABC的平分线,有一个动点P从A向B运动.已知:DC=3cm,DB=4cm,AD=8cm.DP的长为x(cm),那么x的范围是__________
04.如图,已知AB∥CD,PE⊥AB,PF⊥BD,PG⊥CD,垂足分别为E、F、G,且PF=PG=PE,则∠BPD=__________
05.如图,已知AB∥CD,O为∠CAB、∠ACD的平分线的交点,OE⊥AC,且OE=2,则两平行线AB、CD间的距离等于__________
06.如图,AD平分∠BAC,EF⊥AD,垂足为P,EF的延长线于BC的延长线相交于点G.求证:∠G=(∠ACB-∠B)
07.如图,在△ABC中,AB>AC,AD是∠BAC的平分线,P为AC上任意一点.求证:AB-AC>DB-DC
08.如图,在△ABC中,∠BAC=60°,∠ACB=40°,P、Q分别在BC、AC上,并且AP、BQ分别为∠BAC、∠ABC的角平分线上.求证:BQ+AQ=AB+BP
第3讲 轴对称及轴对称变换
考点·方法·破译
1.轴对称及其性质
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫对称轴.
轴对称的两个图形有如下性质:①关于某直线对称的两个图形是全等形;②对称轴是任何一对对应点所连线段的垂直平分线;③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.
2.线段垂直平分线
线段垂直平分线也叫线段中垂线,它反映了与线段的两种关系:①位置关系——垂直;②数量关系——平分.
性质定理:线段垂直平分线上的点与这条线段两个端点的距离相等.
判定定理:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
3.当已知条件中出现了等腰三角形、角平分线、高(或垂线)、或求几条折线段的最小值等情况时,通常考虑作轴对称变换,以“补齐”图形,集中条件.
经典·考题·赏析
【例1】(兰州)如图所示,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展开后是( )
【解法指导】对折问题即是轴对称问题,折痕就是对称轴.故选D.
【变式题组】
01.将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是( )
02.(荆州)如图,将矩形纸片ABCD沿虚线EF折叠,使点A落在点G上,点D落在点H上;然后再沿虚线GH折叠,使B落在点E上,点C落在点F上,叠完后,剪一个直径在BC上的半圆,再展开,则展开后的图形为( )
【例2】(襄樊)如图,在边长为1的正方形网格中,将△ABC向右平移两个单位长度得到△A’B’C’,则与点B’关于x轴对称的点的坐标是( )
A.(0,-1) B.(1,1) C.(2,-1) D.(1,-1)
【解法指导】在△ABC中,点B的坐标为(-1,1),将△ABC向右平移两个单位长度得到△A’B’C’,由点的坐标平移规律可得B’(-1+2,1),即B’(1,1).由关于x轴对称的点的坐标的规律可得点B’关于x轴对称的点的坐标是(1,-1),故应选D.
【变式题组】
01.若点P(-2,3)与点Q(a,b)关于x轴对称,则a、b的值分别是( )
A.-2,3 B.2,3 C.-2,-3 D.2,-3
02.在直角坐标系中,已知点P(-3,2),点Q是点P关于x轴的对称点,将点Q向右平移4个单位得到点R,则点R的坐标是___________.
03.(荆州)已知点P(a+1,2a-1)关于x轴的对称点在第一象限,则a的取值范围为___________.
【例3】如图,将一个直角三角形纸片ABC(∠ACB=90°),沿线段CD折叠,使点B落在B1处,若∠ACB1=70°,则∠ACD=( )
A.30° B.20° C.15° D.10°
【解法指导】由折叠知∠BCD=∠B1CD.设∠ACD=x,则∠BCD=∠B1CD=∠ACB1+∠ACD=70°+x.又∠ACD+∠BCD=∠ACB,即x+(70°+x)=90°,故x=10°.故选D.
【变式题组】
01.(东营)如图,把一个长方形纸片沿EF折叠后,点D、C分别落在点D’、C’的位置.若∠EFB=65°,则∠AED’等于( )
A.70° B.65° C.50° D.25°
02.如图,△ABC中,∠A=30°,以BE为边,将此三角形对折,其次,又以BA为边,再一次对折,C点落在BE上,此时∠CDB=82°,则原三角形中∠B=___________.
03.(江苏)⑴观察与发现:小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.
⑵实践与运用:
将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D’处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.
【例4】如图,在△ABC中,AD为∠BAC的平分线,EF是AD的垂直平分线,E为垂足,EF交BC的延长线于点F,求证:∠B=∠CAF.
【解法指导】∵EF是AD的中垂线,则可得△AEF≌△DEF,∴∠EAF=∠EDF.从而利用角平分线的定义与三角形的外角转化即可.
证明:∵EF是AD的中垂线,∴AE=DE,∠AEF=∠DEF,EF=EF,∴△AEF≌△DEF,∴∠2+∠4=∠3,∴∠3=∠B+∠1,∴∠2+∠4=∠B+∠1,∵∠1=∠2,∴∠B=∠4
【变式题组】
01.如图,点D在△ABC的BC边上,且BC=BD+AD,则点D在__________的垂直平分线上.
02.如图,△ABC中,∠ABC=90°,∠C=15°,DE⊥AC于E,且AE=EC,若AB=3cm,则DC=___________cm.
03.如图,△ABC中,∠BAC=126°,DE、FG分别为AB、AC的垂直平分线,则∠EAG=___________.
04.△ABC中,AB=AC,AB边的垂直平分线交AC于F,若AB=12cm,△BCF的周长为20cm,则△ABC的周长是___________cm.
【例5】(眉山)如图,在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面的备用图中画出所有这样的△DEF.
【解法指导】在正方形格点图中,如果已知条件中没有给对称轴,在找对称轴时,通常找图案居中的水平直线、居中的竖直直线或者斜线作为对称轴.若以图案居中的水平直线为对称轴,所作的△DEF如图①②③所示;若以图案居中的竖直直线为对称轴,所作的△DEF如图④所示;若以图案居中的斜线为对称轴,所作的△DEF如图⑤⑥所示.
【变式题组】
01.(泰州)如图,在2×2的正方形格点图中,有一个以格点为顶点的△ABC,请你找出格点图中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有___________个.
02.(绍兴)如图甲,正方形被划分成16个 全等的三角形,将其中若干个三角形涂黑,且满足下列条件:
⑴涂黑部分的面积是原正方形面积的一半;
⑵涂黑部分成轴对称图形.
如图乙是一种涂法,请在图1-3中分别设计另外三种涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种不同涂法,如图乙与图丙)
【例6】如图,牧童在A处放牛,其家在B处,若牧童从A处出发牵牛到河岸CD处饮水后回家,试问在何处饮水,所求路程最短?
【解法指导】⑴所求问题可转化为CD上取一点M,使其AM+BM为最小;⑵本题利用轴对称知识进行解答.
解:先作点A关于直线CD的对称点A’,连接A’B交CD于点M,则点M为所求,下面证明此时的AM+BM最小.
证明:在CD上任取与M不重合的点M’,
∵AA’关于CD对称,∴CD为线段AA’的中垂线,
∴AM=A’M,M’=A’M’,在△A’M’B中,有A’B<A’M’+BM’,
∴A’M+BM<A’M’+BM’,∴AM+BM<AM’+BM’,
即AM+BM最小.
【变式题组】
01.(山西)设直线l是一条河,P、Q两地相距8千米,P、Q两地到l地距离分别为2千米、5千米,欲在l上的某点M处修建一个水泵站向P、Q两地供水.现在如下四种铺设管道方案,图中的实线表示辅设的管道,则铺设的管道最短的是( )
02.若点A、B是锐角∠MON内两点,请在OM、ON上确定点C、点D,使四边形ABCD周长最小,写出你作图的主要步骤并标明你确定的点.
演练巩固·反馈提高
01.(黄冈)如图,△ABC与△A’B’C’关于直线l对称,且∠A=78°,∠C’=48°,则∠B的度数是( ).
A.48° B.54° C.74° D.78°
02.(泰州)如图,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
03.图1是四边形纸片ABCD,其中∠B=120°,∠D=50°,若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图2所示,则∠C=( )
A.80° B.85° C.95° D.110°
04.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于y轴成轴对称的图形,若点A的坐标是(1,3),则点M和点N的坐标分别是( )
A.M(1,-3),N(-1,-3) B.M(-1,-3),N(-1,3)
C.M(-1,-3),N(1,-3) D.M(-1,3),N(1,-3)
05.点P关于x轴对称的对称点P’的坐标是(-3,5),则点P关于y轴对称的对称点的坐标是( )
A.(3,-5) B.(-5,3) C.(3,5) D.(5,3)
06.已知M(1-a,2a+2)关于y轴对称的点在第二象限,则a的取值范围是( )
A.-1<a<1 B.-1≤a≤1 C.a>1 D.a>-1
07.(杭州)如图,镜子中号码的实际号码是___________.
08.(贵阳)如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为___________cm2.
09.已知点A(2a+3b,-2)和B(8,3a+2b)关于x轴对称,则a+b=___________.
10.如图,在△ABC中,OE、OF分别是AB、AC中垂线,且∠ABO=20°,∠ABC=45°,求∠BAC和∠ACB的度数.
11.如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.
12.如图,P为∠ABC的平分线与AC的垂直平分线的交点,PM⊥BC于M,PN⊥BA的延长线于N.求证:AN=MC.
13.(荆州)有如图“”的8张纸条,用每4张拼成一个正方形图案,拼成的正方形的每一行和每一列中,同色的小正方形仅为2个 ,且使每个正方形图案都是轴对称图形,在网格中画出你拼成的图.(画出的两个图案不能全等)
培优升级·奥赛检测
01.(浙江竞赛试题)如图,直线l1与直线l2相交,∠α=60°,点P在∠α内(不在l1l2上).小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,……如此继续,得到一系列P1、P2、P3……Pn与P重合,则n的最小值是( )
A.5 B.6 C.7 D.8
02.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
⑴如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
⑵如果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是点P1,点P1关于直线l的对称点是P2,求PP2的长.
03.(荆州)某住宅小区拟栽种12棵风景树,若想栽成6行,每行4棵,且6行树所处位置连成线后能组成精美的对称图案,请你仿照举例在下面方框中再设计两种不同的栽树方案.
04.(宜昌)已知:如图,AF平分∠BAC,BC⊥AF,垂足为E,点D与点A关于点E对称,PB分别与线段CF、AF相交于P、M.
⑴求证:AB=CD;
⑵若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
05.在△ABC中,∠BAC=90°,点A关于BC边的对称点为A’,点B关于AC边的对称点为B’,点C关于AB边的对称点为C’,若S△ABC=1,求S△A’B’C’.
06.(湖州市竞赛试题)小王同学在小组数学活动中,给本小组出了这样一道“对称跳棋”题:如图,在作业本上画一条直线l,在直线l两边各放一粒围棋子A、B,使线段AB长a厘米,并关于直线l对称,在图中P1处有一粒跳棋子,P1距A点b厘米、与直线l的距离C厘米,按以下程序起跳:第1次,从P1点以A为对称中心跳至P2点;第2次,从P2点以l为对称轴跳至P3点;第3次,从P3点以B为对称中心跳至P4点;第4次,从P4以l为对称轴跳至P1点;
⑴画出跳棋子这4次跳过的路径并标注出各点字母;(画图工具不限)
⑵棋子按上述程序跳跃2011次后停下,假设a=8,b=6,c=3,计算这时它与A的距离是多少?
07.(湖州)如图,已知平面直角坐标系,A、B两点的坐标分别为A(2,-3),B(4,-1).
⑴若P(p,0)是x轴上的一个动点,则当p=___________时,△PAB的周长最短;
⑵若C(a,0),D(a+3,0)是x轴上的两个动点,则当a=___________时 ,四边形ABCD的周长最短;
⑶设M、N分别为x轴和y轴上的动点,请问:是否存在这样的点M(m,0)、N(0,n),使四边形ABMN的周长最短?若存在,请求出m=___________,n=___________(不必写解答过程);若不存在,请说明理由.
第4讲 等腰三角形
考点·方法·破译
1.等腰三角形及其性质
有两条边相等的三角形叫做等腰三角形,等腰三角形是轴对称图形,因此它的性质有:⑴等腰三角形的两个底角相等(即等边对等角);⑵等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(即等腰三角形三线合一)
2.等腰三角形的判定
证明一个三角形是等腰三角形的基本方法是:⑴从定义入手,证明一个三角形有两条边相等;⑵从角入手,证明一个三角形有两个角相等,依据是等腰三角形判定定理;等角对等边.
3.构造等腰三角形的常用方法
⑴角平分线+平行线=等腰三角形 ⑵角平分线+垂线(或高)=等腰三角形
⑶线段中垂线构造等腰三角形 ⑷将2倍角转化为相等角构造等腰三角形
经典·考题·赏析
等腰三角形一腰上的高与另一腰所成的夹角为400,则这个等腰三角形的底角为________________.
【解法指导】 若问题中涉及到三角形的高,则要分别考虑三角形的高是在三角形的外,三角形内的情况.
解:如图1,当一腰上的高在三角形内时,∠ACD=400,∴∠A=500
∴∠B=∠ACB=
如图2,当一腰上的高在三角形外时,∠ACD=400,∠DAC=500
∴∠DAC=∠B+∠ACB=2∠B
∴∠B=∠ACB=250,故填650或250.
【变式题组】
01.(呼和浩特)在等腰⊿ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )
A.7 B.11 C.7或11 D.7或10
02.(黄冈)在⊿ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为500,则∠B=___________度.
03.(襄樊)在⊿ABC中,AB=AC=12cm,BC=6cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的方向运动.设运动时间为t,那么当t=_________秒时,过D、P两点的直线将⊿ABC的周长分成两个部分,使其中一部分是另一部分的2倍.
【例2】 如图,在⊿ABC中,AB=AC,点D在AC上,AD=BD=BC,求∠A的度数.
【解法指导】 图中的等腰三角形多,可利用等腰三角形的性质,用方程的思想求角的度数.
解:设∠A=x,
∵BD=AD,∴∠A=∠ABD=x,
∴∠BDC=∠A+∠ABD=2x,
∵BD=BC,∴∠C=∠BDC=2x,
∵AB=AC,∴∠ C=∠ABC=2x,
∵在△ABC中, ∠A+∠ABC+∠ACB=180°
∴x+2x+2x=180°,
x=36°,∴∠A=36°.
【变式题组】
01.如图,在⊿ABC中,AB=AC,BD=BC,AD=DE=EB,求∠A的度数.
02.如图,在⊿ABC中,AB=AC,BC=BD= ED=EA,求∠A的大小.
【例3】 已知坐标原点O和点A(2,-2),B是坐标轴上的一点.若⊿AOB是等腰三角形,则这样的点B一共有( )个
A.4 B.5 C.6 D.8
【解法指导】 ⊿AOB是等腰三角形,但不能确定哪条边是等腰三角形的底,因而要分三种情况进行说明①AO=OB,②OA=AB,③BA=BO,又∵B是坐标轴上的点.要考虑x轴与y轴两种情况.
解:①如图1,当OA是底边时,B在OA的中垂线上,又B在坐标轴上,因而B是OA中垂线与坐标轴的交点;
②如图2,当OA为腰时,若O为顶点,则B在以O为圆心,OA为半径的圆上,又B在坐标轴上,因而B是圆与坐标轴的交点;
③如图3,当OA为腰时,若A为顶点,则B在以A为圆心,OA为半径的圆上,又B在坐标轴上,因而B是圆与坐标轴的交点.故选D.
【变式题组】
01.(海南竞赛试题)在平面直角坐标系xOy内,已知A(3,-3),点P是y轴上一点,则使⊿AOP为等腰三角形的点P共有( )
A.2个 B.3个 C.4个 D.5个
02.如图,在平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(0,),点C在坐标平面内.若以A、B、C为顶点构成的三角形是等腰三角形,且底角为30度,则满足条件的点C有_________个.
03.(南昌)如图,已知长方形纸片ABCD,点E是AB的中点,点G是BC上一点,∠BEG>600,现沿直线EG将纸片折叠,使点B落在纸片中的点H处,连接AH,则与∠BEG相等的角的个数为( )
A.4 B.3 C.2 D.1
04.(济南)如图所示,矩形ABCD中,AB=4,BC=,点E是折线段A-D-C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
A.2个 B.3个 C.4个 D.5个
【例4】 (枣庄)两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连结BD,取BD的中点M,连结ME,MC.试判断△EMC的形状,并说明理由.
【解法指导】 判断⊿MEC为等腰直角三角形,M为直角顶点,即想证∠EMC=900,而⊿ABD为等腰三角形,M是BD的中点,若连接AM则有∠AMD=900,因而只需证∠DME=∠AMC,利用全等三角形即可.
解:的形状是等腰直角三角形,理由如下:
连接,由题意得:
.
.
又,
.
.
.
.
又,
.
.
所以的形状是等腰直角三角形.
【变式题组】
01.如图,在等腰直角三角形ABC中,P是斜边BC的中点,以P为直角顶点的两边分别与边AB、AC交于点E、F,当∠EPF绕顶点P旋转时(点E不与A、B重合),⊿PEF也始终是等腰三角形,请你说明理由.
02.如图,在等腰三角形ABC中,∠ACB=900,D是BC的中点,DE⊥AB垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF交AD于G.
⑴求证:AD⊥CF;
⑵连接AF,试判断⊿ACF的形状,并说明理由.
03.如图,⊿ABC中,∠ACB=900,AC=BC,CO为中线.现将一直角三角板顶点放在点O上并绕点O旋转,若三角板的两直角边分别交AC、CB的延长线于点G、H.
⑴试写出图中除AC=BC,OA=OB=OC外其他所有相等的线段;
⑵请选一组你写出的相等线段给予证明.
【例5】 我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
⑴请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
⑵如图,在中,点分别在上,设相交于点,若,.请你写出图中一个与相等的角,并猜想图中哪个四边形是等对边四边形;
⑶在中,如果是不等于的锐角,点分别在上,且.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
【解法指导】 证明两条线段相等时,若两条线段在同一三角形中,可证明它们所对的角相等.若两条线段在不同的三角形中,则证它们所在的两个三角形全等,若三角形不全等,即可通过构造全等三角形或等腰三角形解决问题.
解:⑴如:平行四边形、等腰梯形等
⑵答:与∠A相等的角是∠BOD(或∠COE),四边形DBCE是等对边四边形;
⑶答:此时存在等对边四边形,是四边形DBCE.
证法一:如图1,作CG⊥BE于G点,作BF⊥CD交CD延长线于F点.
∵∠DCB=∠EBC=∠A,BC为公共边,
∴△BCF≌△CBG,
∴BF=CG,
∵∠BDF=∠ABE+∠EBC+∠DCB,∠BEC=∠ABE+∠A,
∴∠BDF=∠BEC,
可证△BDF≌△CEG,
∴BD=CE
∴四边形DBCE是等边四边形.
证法二:如图2,以C为顶点作∠FCB=∠DBC,CF交BE于F点.
∵∠DCB=∠EBC=∠A,BC为公共边,
∴△BDC≌△CFB,
∴BD=CF,∠BDC=∠CFB,
∴∠ADC=∠CFE,
∵∠ADC=∠DCB+∠EBC+∠ABE,∠FEC=∠A+∠ABE,
∴∠ADC=∠FEC,
∴∠FEC=∠CFE,
∴CF=CE,∴BD=CE,
∴四边形DBCE是等边四边形.
【变式题组】
01.如图,在ABC中,∠B=2∠C,AD为∠BAC的平分线.求证:AC=AB+BD.
02.(天津初赛试题)如图,在四边形ABCD中,∠ACB=∠BAD=1050,∠ABC=∠ADC=450,若AB=2,求CD的长.
03.如图,在ABC中,AB=AC,D在AB上,F在AC延长线上,BD=CF.求证DE=EF.
【变式题组】
01.(重庆)已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为( )
A.200 B.1200 C.200或1200 D.3600
02.(云南)已知等腰三角形的两边分别为6和3,则此等腰三角形周长为( )
A.9 B.15 C.15 D.12或15
03.(云南)如图,等腰ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则BEC的周长为( )
A.13 B.14 C.15 D.16
04.如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=180,则∠GEF的度数是( )
A.800 B.900 C.1000 D.1080
05.如图,RtABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中不正确的是( )
A.∠ACD=∠B B.CH=CE=EF C.CH=HD D.AC=AF
06.如图,ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①BDF和CEF都是等腰三角形;②DE=BD+CE;③ADE的周长等于AB与AC的和;④BF=CF.其中正确的有( )
A.①②③ B.①②③④ C.①② D.①
07.(武汉)如图,已知O是四边形ABCD内一点,OA=OB=OC, ∠ABC=∠ADC=700,则∠DAO+∠DCO的大小是( )
A.700 B.1100 C.1400 D.1500
08.(滨州)已知等腰ABC的周长为10,若设腰长为x,则x的取值范围是____________.
09.如图所示,在ABC中,已知AB=AC,∠A=360,BC=2,BD是ABC的角平分线,则AD=___________.
10.(威海)如图,AB=AC,BD=BC,若∠A=400,则∠ABD的度数是_________.
11.(乌鲁木齐) 在一次数学课上,王老师在黑板上画出图6,并写下了四个等式:
①,②,③,④.
要求同学从这四个等式中选出两个作为条件,推出是等腰三角形.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)
已知:
求证:是等腰三角形.
证明:
12.(泰安) 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,在同一条直线上,连结.
⑴请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
⑵证明:.
13.(包头)如图,已知中,厘米,厘米,点为的中点.
⑴如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?
⑵若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?
14.(临沂)如图1,已知中,,,把一块含角的直角三角板的直角顶点放在的中点上(直角三角板的短直角边为,长直角边为),将直角三角板绕点按逆时针方向旋转.
⑴在图1中,交于,交于.
①证明;
②在这一旋转过程中,直角三角板与的重叠部分为四边形,请说明四边形的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
⑵继续旋转至如图2的位置,延长交于,延长交于,是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
⑶继续旋转至如图3的位置,延长交于,延长交于,是否仍然成立?请写出结论,不用证明.
培优升级·奥赛检测
01.如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:①GA=GP;②③BP垂直平分CE;④FP=FC;其中正确的判断有( )
A.只有①② B.只有③④ C.只有①③④ D.只有①②③④
02.如图,点A是网格图形中的一个网格图形中的一个格点(小正方形的顶点),图中每个小正方形的边长为1,以A为其中的一个顶点,面积等于2.5的格点等腰直角三角形(三角形的三个顶点都是格点)的个数是( )
A.10个 B.12个 C.14个 D.16个
03.如图,在ABC中,AB=BC,MN=NA, ∠BAM=∠NAC,则∠MAC=_________.
04.如图,AA’、BB’分别是∠EAB、∠DBC的平分线,若AA’=BB’=AB.则∠BAC的度数为______________.
05.(全国联赛)在等腰RtABC中,AC=BC=1,M是BC的中点,CE⊥AM于E,交AB于F.则 =_____________
06.如图,在ABC中,AB=AC,EF为过点A的任意一条直线,CF⊥BC, BE⊥BC.求证:AE=AF.
07.(湖州市竞赛试题)如图,在RtABC中,∠ACB=900,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE,求证:FK∥AB
08.(四川省初二数学联赛试题)有一等腰钝角三角形纸片,若能从一个顶点出发,将其剪成两个等腰三角形纸片,求等腰三角形纸片的顶角的度数.
09.如图,在ABC中,∠ABC=460,D是边BC上一点,DC=AB, ∠DAB=210,求∠CAD的度数.
10.(浙江省杭州市中考试题)如图,在等腰△中,是底边上的高线,点是线段上不与端点重合的任意一点,连接交于点,连接交于点.
(1) 证明:;
(2) 证明:;
(3) 以线段和为边构成一个新的三角形(点与点重合于点),记△和△的面积分别为和,如果存在点,能使得 , 求∠的取值范围.
11.如图,已知在△中,AB=AC,∠BAC=900,AD=AE, AF⊥BE交BC于F,过F作FG⊥CD交BE的延长线于G.求证:BG=AF+FG
第五讲 等边三角形
考点 方法 破译
1.等边三角形及其性质:三边都相等的三角形叫做等边三角形,等边三角形的三个内角都相等,并且每一个角都等于60.等边三角形是轴对称图形,对称轴是顶角平分线或底边上的高、中线所在直线;
2.等边三角形的判定:三边都相等的三角形是等边三角形;三个角都相等的三角形是等边三角形;有一个角为60°的等腰三角形是等边三角形;
3.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,反之也成立.
经典 考题 赏析
【例1】如图,△DAC和△EBC均是等边三角形,A、C、B三点在一条直线上.AE、BD分别与CD、CE交于点M、N.
(1)求证:△ACE≌△DCB;
(2)求∠AFD的度数;
(3)判断△CMN的形状
【解法指导】根据等边三角形的性质,利用全等三角形中边角的关系可解决问题.
解:(1)∵等边三角形DAC与等边三角形EBC ∴AC=DC,CE=CB,∠ACD=∠BCE=60°
∴ ∠ACE=∠DCB
∴在△ACE和△DCB中,,∴△ACE≌△DCB
(2) ∵∠ACE≌∠DCB, ∴∠1=∠2
又∵∠1+∠DFA==∠2+∠ACD ∴∠AFD=∠ACD=60°
(3) 在△ACM和△DCN中,
∴△ACM≌△DCN ∴CM=CN
又∵∠DCN =60°∴△CMN是等边三角形.
【变式题组】
01.(天津)如图,P、Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,
则∠BAC的大小等于__________ 度
02.(荆州)如图,D是等边△ABC的边AB上的一动点,以CD为一边向上作等边△EDC,连接AE,找出图中的一组全等三角形,并说明理由.
03.如图,在正△ABC中,D,E分别是BC、AC上的一点,且AE=CD .AD与BE相交于点P,且BQ⊥AD于Q.求证BP=2PQ
04.(黄冈)如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q是BC延长线上一点,当PA=CQ时,连接PQ交AC于D,求DE的长.
【例2】P是△ABC内一点,∠PBC=30°,∠PBA=8°,且∠PAB=∠PAC=22°,求∠APC的度数
【解法指导】 由于∠PAB =∠PAC,因而PA平分∠BAC,根据角平分线的特点可构造全等三角形,其方法一:在AB边上截取;方法二:延长AC边,又由于∠BPA=150°是特殊角,考虑∠BPA的完整性,因而取方法二的可能性更大.
解:延长AC到D,使AD=AB,连接PD、BD,∵∠PBA=8°∠PAB =22°
∴∠BPA=150°,在△ABP和△ADP中,∴△ABP≌△ADP ∴∠APB=∠APD = 150°,BP=DP ,∠PBA=∠APD =8°
∴∠BPD=60°, ∴△BPD是正三角形
∵∠PBC=30° ∴∠PBC=∠DBC
在△PBC和△DBC中,
∴△PBC≌△DBC , ∴PC=CD ∴∠CPD=∠CDP=8°
∴∠APC=∠APD一∠CPD=150°一8°=142°
【变式题组】
01.如图,D是等边三角形ABC内一点,E为ABC外部一点,满足DA=DB,BE=BA,∠DBE=∠DBC.求∠BED的度数.
02.如图.D是△ABC外一点.AB=AC=BD+CD,∠ABD=60°求∠ACD的度数.
【例3】如图(1),△ABC等边三角形,△BDC是顶角120°的等腰三角形,以D为顶点作60°的角,它的两边分别与AB、AC交于点M和N,连接MN.
(1)探究:MN、NC之间的关系,并加以证明;
(2)若点M、N分别在射线AB、CA上,其他条件不变,再探究线段BM、MN、NC之间的关系,在图(2)中画出相应的图形.并就结论说明理由
【解法指导】对于(1),这时在△DMB中,有∠DBM=∠DBC+∠CBA=30°+60°=90°
为了把BM,MN,NC集中到一个三角形中去,将△DMB 绕D点顺时针旋转120°得到△DGC.如图(3).从而有MB=GC.而此时恰又有△MND≌△GND·得MN=NG=NC+CG=NC+BM.对于(2),此时的图形(4),仍作(1)中的旋转,类似地可以推得MN=CN一BM
解(1)关系为MN=BM+NC
证明:延长AC到G,使CG=BM,连接DG,如图(3)
∠ABD=∠ABC+∠CBD=60°十30°=90°同理也有∠ACD=90°
在△DMB和△DGC中; DB=DC.BM=CG
∴△DMB≌△DGC ∴DM=DG.∠MDB=∠GDC.
在△MND和△GND中,ND公用,DM=DG,∠MDN=60°
∠GDN=∠GDC+∠DCN=∠MDB+∠CDN=60°
∴△MND≌△GND ∴ MN=GN=GC十NC=BM+NC
(2)此时.图形如图(4),有关系式MN=CN—BM理由如下:
在CN上截取GG=BM.连接DG,如图(4)与(1)中情况类似.可推得
∠ABD=∠ACD=90°.且Rt△DMB≌△DGC ,得DM=DG.∠MDB=∠GDC
仍与(1)中情况娄似,可推得△MND≌△GND.就有MN=GN=NC—CG=NC—BM.
【变式题组】
01.用两个全等的等边三角形△ABC和△ACD拼成四边形ABCD,把一个含60°角的三角尺与这个四边形叠合,使三角尺的60°角的顶点与点A重合.两边分别与AB、AC重合,将三角尺绕点A按逆时针方向旋转
(1)当三角尺的两边分别与四边形的两边BC、CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;
(2)当三角尺的两边分别与四边形的两边BC、CD的延长线相交于点F时(如图2),你在(1)中得到的结论还成立吗,简要说明理由.
02.如图.四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°
求证:AC=BC+DC.
巩固练习 反馈提高
01.如图.△ABC是等边三角形,AD⊥BC,点E在AC上,且AE=AD,则∠DEC=( )
A 105° B 85° C 95° D 75°
第1题图 第2题图
02.如图,等边△ABC,D在AC上,延长BC到E.使CE=CD,若BD=DE,给出下列结论:① BD平分∠ABC ② AD = AB ③ CE= BC ④∠A=2∠E,其中正确结论的个数是( )
A.4个 B 3个 C 2个 D 1个
03.(河北)如图,等边△ABC的边长为1cm,D、E分别是AB、AC 上的点,将△ABC沿直线DE折叠,点A落在A’处,且A’在△ABC外部,则阴影部分图形的周长为__________ cm
04.在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°,得到线段OD,要使点D恰好落在BC上,则AP=__________.
05.如图,△ABC是等边三角形,D、E、F分别在AB、BC、AC上,且DE⊥BC,EF⊥AC,FD⊥AB,试判断△DEF是否为等边三角形,并说明理由.
06.请你用三种不同的分割方法,将图中的三个正三角形分别分割成四个等腰三角形(在图中画出分割线,并标出必要的角的度数) .
07.如图,点D是等边△ABC边AB上的一点.AB=3AD,DE⊥BC于点E,AE、CD相交于点F
(1)求证:△ACD≌△BAE:
(2)过点C作CG⊥AE,垂足为点G,探究CF与FG之间的数量关系,并证明.
08.如图:△ABC是等边三角形,D是AB边上的点,将线段DB绕点D顺时针旋转60°得到线段DE,延长ED交AC于点F,连接DC,AE.
求证:△ADE≌△DFC
09.如图:△ABC是等边三角形,点D、E分别在CA、AB的延长线上, AD=BE.DB的延长线交EC于F.
求证:(1)DB=EC;(2) ∠BFC=60°
10.(常德)如图1,若△ABC与△ADE为等边三角形,M、N分别是EB、CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕点A旋转到图2的位置时,CD=BE是否仍然成立? 若成立请证明,若不成立请说明理由;
(2) 当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形? 若成立请证明,若不成立请说明理由.
第06讲 实 数
考点·方法·破译
1.平方根与立方根:
若=a(a≥0)则x叫做a的平方根,记为:a的平方根为x=±,其中a的平方根为x=叫做a的算术平方根.
若x3=a,则x叫做a的立方根.记为:a的立方根为x=.
2.无限不循环小数叫做无理数,有理数和无理数统称实数.实数与数轴上的点一一对应.任何有理数都可以表示为分数(p、q是两个互质的整数,且q≠0)的形式.
3非负数:
实数的绝对值,实数的偶次幂,非负数的算术平方根(或偶次方根)都是非负数.即>0,≥0(n为正整数),≥0(a≥0) .
经典·考题·赏析
【例1】若2m-4与3m-1是同一个数的平方根,求m的值.
【解法指导】一个正数的平方根有两个,并且这两个数互为相反数.∵2m ?4与3m?l是同一个数的平方根,∴2m?4 +3m?l=0,5m=5,m=l.
【变式题组】
01.一个数的立方根与它的算术平方根相等,则这个数是____.
02.已知m是小于的最大整数,则m的平方根是____.
03.的立方根是____.
04.如图,有一个数值转化器,当输入的x为64时,输出的y是____.
【例2】(全国竞赛)已知非零实数a、b满足,则a+b等于( )
A.-1 B. 0 C.1 D.2
【解法指导】若有意义,∵a、b为非零实数,∴b2>0∴a-3≥0 a≥3
∵
∴,∴.
∴,∴,故选C.
【变式题组】
0l.在实数范围内,等式=0成立,则ab=____.
02.若,则的平方根是____.
03.(天津)若x、y为实数,且,则的值为( )
A.1 B.-1 C.2 D.-2
04.已知x是实数,则的值是( )
A. B. C. D.无法确定
【例3】若a、b都为有理效,且满足.求a+b的平方根.
【解法指导】任何两个有理数的和、差、积、商(除数不为0)还是有理数,但两个无理数的和、差、积、商(除数不为0)不一定是无理数.∵,
∴ 即,∴,
a +b=12 +13=25.
∴a+b的平方根为:.
【变式题组】
01.(西安市竞赛题)已知m、n是有理数,且(+2)m+(3-2)n+7=0求m、n.
02.(希望杯试题)设x、y都是有理数,且满足方程()x+()y?4?=0,则x?y=____.
【例4】若a为?2的整数部分,b?1是9的平方根,且,求a+b的值.
【解法指导】一个实数由小数部分与整数部分组成,?2=整数部分+小数部分.整数部分估算可得2,则小数部分=?2 ?2=?4.∵a=2,b?1=±3 ,∴b=-2或4
∵.∴a【变式题组】
01.若3+的小数部分是a,3?的小数部分是b,则a+b的值为____.
02.的整数部分为a,小数部分为b,则(+a)·b=____.
演练巩固 反馈提高
0l.下列说法正确的是( )
A.-2是(-2)2的算术平方根 B.3是-9的算术平方根
C. 16的平方根是±4 D.27的立方根是±3
02.设,b= -2,,则a、b、c的大小关系是( )
A.a03.下列各组数中,互为相反数的是( )
A.-9与81的平方根 B.4与 C.4与 D.3与
04.在实数1.414,,0.,5?,,3.,中无理数有( )
A.2个 B.3个 C.4个 D. 5个
05.实数a、b在数轴上表示的位置如图所示,则( )
A.b>a B.
C. -a<b D.-b>a
06.现有四个无理数,,,,其中在+1与+1之间的有( )
A. 1个 B.2个 C. 3个 D .4个
07.设m是的平方根,n=.则m,n的关系是( )
A. m=±n B.m=n C .m=-n D.
08.(烟台)如图,数轴上 A、B两点表示的数分别为-1和,点B关于点A的对称点C,则点C所表示的数为( )
A.-2 B.-1 C.-2 + D.l +
09.点A在数轴上和原点相距个单位,点B在数轴上和原点相距3个单位,且点B在点A左边,则A、B之间的距离为____.
10.用计算器探索:已知按一定规律排列的一组数:1,,…,,.如果从中选出若干个数,使它的和大于3,那么至少要选____个数.
11.对于任意不相等的两个数a、b,定义一种运算※如下:a※b=,如3※2==.那么12.※4=____.
12.(长沙中考题)已知a、b为两个连续整数,且a<13.对实数a、b,定义运算“*”,如下a*b=,已知3*m =36,则实数m=____.
14.设a是大于1的实数.若a,,在数轴上对应的点分别是A、B、C,则三点在数轴上从左自右的顺序是____.
15.如图,直径为1的圆与数轴有唯一的公共点P.点P表示的实数为-1.如果该圆沿数轴正方向滚动一周后与数轴的公共点为P′,那么点P′所表示的数是____.
16.已知整数x、y满足+2=,求x、y.
17.已知2a?1的平方根是±3,3a+b?1的算术平方根是4,求a+b+1的立方根.
18.小颖同学在电脑上做扇形滚动的游戏,如图有一圆心角为60°,半径为1个单位长的扇形放置在数轴上,当扇形在数轴上做无滑动的滚动时,当B点恰好落在数轴上时,(1)求此时B点所对的数;(2)求圆心O移动的路程.
19.若b= + +3l,且a+11的算术平方根为m,4b+1的立方根为n,求(mn?2)(3mn +4)的平方根与立方根.
20.若x、y为实数,且(x?y+1)2与互为相反数,求的值.
培优升级 奥赛检测
01.(荆州市八年级数学联赛试题)一个正数x的两个平方根分别是a+1与a?3,则a值为( )
A. 2 B.-1 C. 1 D. 0
02.(黄冈竞赛)代数式++的最小值是( )
A.0 B. 1+ C.1 D. 2
03.代数式?2的最小值为____.
04.设a、b为有理数,且a、b满足等式a2+3b+b=21?5,则a+b=____.
05.若=1,且3=4,则在数轴上表示a、b两数对应点的距离为____.
06.已知实数a满足,则a? 20092=_______.
07.若m满足关系式 ,试确定m的值.
08.(全国联赛)若a、b满足=7,S=,求S的取值范围.
09.(北京市初二年级竞赛试题)已知010.(北京竞赛试题)已知实数a、b、x、y满足y+,,求的值.
11.(全国竞赛试题)巳知x=,a、b为互质的正整数.且a≤8,?1 (1)试写出一个满足条件的x;(2)求所有满足条件的x.
第7讲 变量与函数
考点·方法·破译
1.函数的概念及其表示方法
⑴函数的定义:在一个变化过程中,有两个变量x和y,对于给定的每一个x值,y都有唯一确定的值与其对应,那么,x是自变量,y是x的函数.
⑵函数的表示方法
①解析法:用含有自变量的代数式表示函数的方法;
②列表法:把自变量x的一系列值和函数y的对应值列成表格来表示函数的方法;
③图象法:用图象表示函数关系的方法.
2.自变量取值范围的确定
自变量的取值必须使含自变量的代数式都有意义,且必须符合实际问题的要求.
经典·考题·赏析
【例1】(兰州)函数中自变量x的取值范围是( )
A. x≤2 B. x=3 C. x<2且x≠3 D.x≤2且x≠3
【解法指导】 求x的取值范围,可根据题目要求列出下列式子: 解得x≤2且x≠3, 故选A
【变式题组】
01.(大兴安岭)函数中,自变量x 的取值范围是________
02.(芜湖)函数中自变量x的取值范围是_________
03.函数中自变量x的取值范围是_________
04.已知函数y=-2x+1中的自变量x的取值范围是0<x<10,则y的取值范围是______
【例2】汽车由北京驶往相距850km的沈阳,它的平均速度为80km/h,求汽车距沈阳的路程s(km)与行驶时间t(h)的函数关系式,写出自变量的取值范围
【解法指导】⑴此题属于行程问题,其基本数量关系是:速度时间=路程.因此汽车行驶t(h)的路程是80t(km)与汽车距沈阳的路程s(km)及北京与沈阳的距离850km之间的等量关系是80t+s=850;(2)由于s与t都应是非负数可确定自变量的取值范围.
解:由题意得,s=850-80t
又由于 即 解得 0≤t≤
因此汽车距沈阳的路程s与时间t的函数关系式为s=850-80t,自变量的取值范围是0≤t≤
【变式题组】
01.已知三角形的面积为20cm2,设它的底边长为x(cm),则底边上的高y(cm)关于x的函数关系式为______,自变量的取值范围是__________.
02.等腰三角形的周长是40cm,腰长y(cm)与底边长x(cm)关系的函数解析式正确的是( )
A. y=-0.5x+20(0<x<20) B.y=-0.5x+20(10<x<20)
C. y=-2x+40(10<x<20) D.y=-2x+40(0<x<20)
03. 某市为了鼓劲居民节约用水,对自来水用户按如下标准收费:若每月每户用水不超过12米3,按每立方米 a 元收费;若超过12米3,则超过部分每立方米按2a元收费.某户居民五月份交水费y(元)与用水量x(米3)(x>12)之间的关系式为______,若该月交水费20a元,则这个月实际用水______米3.
【例3】下列曲线中,表示y不是x的函数的是( )
【解法指导】 要根据曲线判断所给变化中,y是否是x的函数,则需要根据曲线观察对于x的每一个确定的值,是否y都有惟一的一个确定的值与之对应,如果是,则y就是x的函数,观察所给的四个选项,可知B中所示的曲线,当x取一个值时,y有两个值与之对应,根据函数的定义可知y不是x的函数,应选B.
【变式题组】
01.图中分给给出了x与y的对应关系,其中y是x的函数是( )
02.下列函数中,与y=x表示同一个函数的是( )
A. B. C. D.
【例4】 如右图,圆柱形开口杯的底部固定在长方体池底,向水池匀速注入水(倒在杯外),水池中水面高度是h ,注水时间是t,则h与t之间的关系大致为下面图中的( )
【解法指导】由题意知,此注水过程中分为三段:⑴由于圆柱形开口杯底部固定在长方体水池,也就是说水池被开口杯占据了一部分空间,因此注水时水池中水面上升的速度较快,其图象是一段自原点出发较陡的上升线段;⑵当水的与开口杯口等高时,水开始注入开口杯,也就是说水池中水面高度不变,则其图象是一段平行于t轴的水平线段;⑶当开口杯注满时,水位开始上升,由于水池的此部分空间比⑴段大,因此水池中水面上升的速度要比⑴段速度慢,则其图象是一段比⑴段中上升线段较缓的上升线段,由此可知答案应选B.
【变式题组】
01.如图所示,向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度h与注水时间t的函数关系式,大致是下列图象中的( )
02.某蓄水池的横截面示意图如图所示,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出,下面的图象能大致表示水的深度h和放水时间t之间的关系的是( )
03.用均匀的速度向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图表示(图中OAB为一折线),这个容器的形状是图中的( )
【例5】 已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边线运动,运动路径为:G→C→D→E→F→H相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象,如图2,若AB=6cm,则下列四个结论中正确的个数有( )
图1中的BC边长是8cm
图2中的M点表示第4秒时y的值为24cm2
图中的CD长是4cm
图2中的N点表示第12秒时y的值为18cm2
A. 1个 B. 2个 C. 3个 D. 4个
【解法指导】 若把点P由G→C→D→E→F→H对应的图象分别记为第I段、第II段、第III段、第IV段、第V段,则从图1和图2的对应情况可知:
由I的两端点横坐标,知由G到C运动2秒,可得GC=4cm,即BC=8cm;
∴a正确
M点的纵坐标等于S△ABD=;∴b正确
∵P在CD上的时间从图2知为2秒,∴CD==24cm
ABCDEFGH的周长为(AB+BC+DE)2=40cm
∴ AH=
∴ y= ∴d正确 故选D.
【变式题组】
01.(莆田)如图1,在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到的位置是( )
A. N处 B. P处 C. Q处 D.M处
02.(重庆綦江)如图1,在直角梯形ABCD中,动点P从点B出发,沿BC、CD运动至点D停止,设点P运动的路径为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
A. 3 B. 4 C. 5
演练巩固·反馈提高
01.(益阳)某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,图中描述了他上学的情景,下列说法错误的是( )
A. 修车时间为15分钟 B. 学校离家的距离为2000米
C. 到达学校时共用时间20分钟 D.自行车发生故障时离家距离为1000米
02.(宜昌)由于干旱,某水库的蓄水量随时间的增加而直线下降,若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( )
A. 干旱开始时,蓄水量每天减少20万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱第50天时,蓄水量为1200万米3
03.(黑龙江大兴安岭)一个水池接有甲、乙、丙三个水管,先打开甲,一段时间后再打开乙,水池注满水后关闭甲,现时打开丙,直到水池中的水排空,水池中的水量V(m3)与时间t(h)之间的函数关系如图,则关于三个水管每小时的水流量,下列判断正确的是
A. 乙>甲 B. 丙>甲 C.甲>乙 D.丙>乙
04.(杭州)已知点P(x,y)在函数的图象上,那么点P应在平面直角坐标系中的( )
A. 第一象限 B.第二象限 C. 第三象限 D.第四象限
05.(大连)函数的自变量x的取值范围是( )
A.x≥-2 B. x>-2且x≠2 C.x≥0且x≠2 D.x≥-2且x≠2
06.已知某一函数的图象如图所示,根据图象回答下列问题.
⑴确定自变量的取值范围;
⑵求当x=-4,-2时y的值是多少?
⑶求当y=0,4时,x的值是多少?
⑷当x取何值时y的值最大?当x何值时y的值最小?
(5)当x在什么范围内取值时y随x的增大而增大?当x在什么范围内取值时y随x的增大而减小?
07.甲、乙两人在一次赛跑中,路程s与时间t的关系式如图所示,那么你可知道:
⑴这是一次_________米的赛跑;
⑵甲、乙两人中先跑到终点的是_______
(3) 乙在这次赛跑中的速度为______米/秒
第8讲 一次函数的图象与性质
考点·方法·破译
1.一次函数及图象:
⑴形如y=kx+b(k,b为常数,且k≠0),则y叫做x的一次函数,当b=0,k≠0时,y叫做x的正比例函数.
⑵正比例函数y=kx(k≠0)的图象是经过(0,0),(1,k)两点的直线,一次函数y=kx+b(k≠0)是经过(0,b)、(-,0)两点的直线.
2.一次函数的性质:
当k>0时,y随自变量x的增大而增大;当k<0时,y随x的增大而减小.
3.函数y=kx+b中的系数符号,决定图象的大致位置的增减性.
经典·考题·赏析
【例1】(山东)函数y=ax+b①和y=bx+a②(ab≠0)在同一坐标系中的图象可能是( )
【解法指导】A中①a>0,b>0,②b<0,a<0矛盾.B中①a<0,b<0,矛盾.C中①a>0,b>0②b>0,a=0矛盾.D中①a>0,b<0②b<0,a>0,故选D.
【变式题组】
01.(河北)如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
02.(安徽)已知函数y=kx+b的图象如左图,则y=2kx+b的图象可能是( )
03.下列图象中,表示一次函数y=mx+n与正比例函数y=mnx(m、n为常数,则mn≠0)的图象是( )
【例2】(绍兴)如图,一次函数y=x+5的图象经过点P(a,b)和Q(c,d)则a(c-d)-b(c-d)的值为_______.
【解法指导】因为点P(a,b),Q(c,d)在一次函数图象上,∴b=a+5,d=c+5∴a-b=-5,c-d=-5,a(c-d)-b(c-d)=(c-d)(a-b)=(-5)×(-5)=25
【变式题组】
01.如图一条直线l经过不同三点A(a,b),B(b,a)C(a-b,b-a)则直线l经过( )
A.第二、四象限 B.第一、三象限 C.第二、三、四象限 D.第一、三、四象限
02.(南京市八年级竞赛试题)已知三点A(2,3),B(5,4)C(-4,1)依次连接这三点,则( )
A.构成等边三角形B.构成直角三角形C.构成锐角三角形D.三点在同一条直线上
03.(四川省初二数学联赛试题)已知一次函数y=ax+b的图象经过点(0,1),它与坐标轴围成的图是等腰直角三角形,则a的值为_______.
【例3】如图,已知正方形ABCD的顶点坐标为A(1,1)、B(3,1)、C(3,3)、D(1,3),直线y=2x+b交AB于点E,交CD于点F.直线与y轴的交点为(0,b),则b的变化范围是_____.
【解法指导】直线y=2x+b是平行于直线y=2x的直线,当直线经过B点时,b最小,当x=3时,y=1
∴1=2×3+b, b=-5
当直线经过D点时,b最大,
所以当x=1时,y=3
∴3=2×1+b, b=1
∴-5≤b≤1
【变式题组】
01.线段y=-x+a(1≤b≤3),当a的值由-1增加到2时,该线段运动所经过的平面区域的面积为( )
A.6 B.8 C.9 D.10
02.(新知杯上海)在平面直角坐标系中有两点P(-1,1),Q(2,2),函数y=kx-1的图象与线段PQ延长线相交(交点不包括Q),则实数k的取值范围是_________.
03.(济南)阅读下面的材料:在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1= k2,且b1=b2,我们就称直线l1与直线l2平行.解答下面的问题:
⑴求过点P(1,4)且与已知直线y=-2x-1平行的直线l的函数表达式,并画出直线l的图象;
⑵设直线l分别与y轴、x轴交于点A、B,如果直线m:y=kx+t(t>0)与直线平行且交于x轴于点C,求出△ABC的面积S关于t的函数关系式.
【例4】已知一次函数y=kx+b,当自变量取值范围是2≤x≤6时,函数值的取值范围5≤y≤9.求此函数的解析式.
【解法指导】⑴当k>0,y随x的增大而增大,∴y=kx+b经过(2,5),(6,9)两点
∴∴,∴y=x+3
⑵当k<0,y随x的增大而减小,∴y=kx+b经过(2,9),(6,5)两点
∴∴,∴y=-x+11
∴所求解析式为y=x+3或y=-x+11
【变式题组】
01.已知一次函数y=kx+b,当-3≤x≤1时,对应y的值为1≤y≤9,则kb的值为( )
A.4 B. -6 C.-4或21 D.-6或14
02.(遂宁)已知整数x满足-5≤x≤5,y1=x+1,y2=2x+4,对任意一个x,m都取y1,、y2中的最小值,则m的最大值是( )
A.1 B. 2 C.24 D.-9
【例5】如图,直线y=-5x-5与x轴交于A,与y轴交于B,直线y=kx+b与x轴交于 C,与y轴交于B点,CD⊥AB交y轴于E.若CE=AB,求直线BC 的解析式.
【解法指导】由CE=AB,CD⊥AB可得△AOB≌△EOC,因而OB=OC而y=-5x-5与y轴交于B
∴B(0,-5)
∴C(5,0),而直线BC经过(0,-5),(5,0)可求得解析式y=x-5
【变式题组】
01.如图,在平面直角坐标系中,点P(x,y)是直线y=-x+6第一象限上的点,点A(5,0),O是坐标原点,△PAO的面积S.
⑴求S与x的函数关系式,并写出x的取值范围;
⑵探究:当P点运动到什么位置时△PAO的面积为10.
02.如图,直线l:y=-x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
⑴求A、B两点的坐标;
⑵求△COM的面积S与M的移动时间t之间的函数关系式;
⑶当t为何值时,△COM≌△AOB,并求此时M点的坐标.
03.如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过A(0,2)、B(4,2)两点.
⑴求直线AB的解析式;
⑵点C的坐标为(0,1),过点C作CD⊥AO交AB于D. x轴上的点P和A、B、C、D、O中的两个点所构成的三角形与△ACD全等,这样的三角形有_____个,请子啊图中画出其中两个三角形的示意图.
【例6】如图,已知直线y=-x+2与x轴、y轴分别交于点A和点B.另一条直线y=kx+b(k≠0)经过(1,0),且把△AOB分成两部分.⑴若△AOB被分成的两部分面积相等,求k和b的值;⑵若△AOB被分成的两部分的面积比为1:5,求k和b的值.
【解法指导】欲求k和b的值,需知道直线y=kx+b(k≠0)经过两已知点,而点C(1,0)在直线上,因而只需求出另一点的坐标即可.
解:⑴由题意得(2,0)、B(0,2),∴C为OA的中点,因而直线y=kx+b过OA中点且平分△AOB的面积时只可能韦中线BC.
∴y=kx+b经过C(1,0),(0,2)
∴∴k=2 b=2
⑵①设y=kx+b与OB交于M(0,t)则有S△OMC=S△CAN,∴MN∥x轴,∴N(,)
∴直线y=kx+b经过,),(1,0)∴ ∴
【变式题组】
01.如图,在平面直角坐标系xOy,已知直线AC的解析式为y=-x+2,直线AC交x轴于点C,交于y轴于点A.
⑴若一个等腰直角三角形OBD的顶点D与点C重合,直角顶点B在第一象限内,请直接写出点B的坐标;
⑵过点B作x轴的垂线l,在l上是否存一点P,使得△AOP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
⑶试在直线AC上求出到两坐标轴距离相等的所有点的坐标.
02.(浙江杭州)已知,直线y=-与x轴、y轴分别交于点A、B,以线段AB为直角边的第一象限内作等腰Rt△ABC,°,且点P(1,a)为坐标系中的一个动点.
⑴求三角形ABC的面积S△ABC;
⑵证明不论a取任何实数,三角形BOP的面积是一个常数;
⑶要使得△ABC和△ABP的面积相等,求实数a的值.
演练巩固·反馈提高
01.(芜湖)关于x的一次函数y=kx+k2+1的图象可能正确的是( )
02.一次函数y=kx-b和正比例函数y=kbx在同一直角坐标系内的大致图象不可能的是()
03.一次函数y=(m-1)x+m2+2的图象与y轴的交点的纵坐标是3,则m的值是()
A. B. C.-1 D.-2
04.直线y1=kx+b过第一、二、四象限,则直线y2=bx-k不经过()
A. 第一象限 B.第二象限 C.第三象限 D.第四象限
05.已知一次函数y=(1-2m)x+m-2,函数y随着x的增大而减小,且其图象不经过第一象限,则m的取值范围是( )
A.m> B.m≤2 C.<m<2 D. <m≤2
06.如图,点A、B、C、D在一次函数y=-2x+m的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A. 1 B.3 C.3(m-1) D. (m-2)
07.(绍兴)如图,在x轴上有五个点,它们横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0,则图中阴影部分的面积是( )
A. 12.5 B.25 C.12.5a D. 25a
08.(重庆)如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致是( )
09.(日照)如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A.(0,0) B.(,-) C.(-,-) D.(-,-)
10.(义务)李老师给出了一个函数,甲、乙、丙三位同学分别指出这个函数的一个特征.甲:它的图象经过第一象限;乙:它的图象经过第二象限;丙:在第一象限内函数值y随x增大而增大.在你学习的函数中,写出一个满足上述特征的函数解析式_________.
11.观察下列各直角坐标系中的直线AB,点P(x,y)是线段AB上的点,且x、y都是整数,请根据图中所包含的规律,回答下列问题:
⑴第5个图中满足条件的点P个数是_______;
⑵第n个图中满足条件的点P个数m与n之间的关系是________.
12.(十堰)直线y=kx+b经过点A(-2,0)和y轴上的一点B,如果△ABO(O为坐标原点)的面积为2,则b的值为________.
13.如图,长方形OABC的顶点B的坐标为(6,4),直线y=-x+b恰好平分长方形的面积,则b=_______.
14.如图,点B、C分别在两条直线y=2x和y=kx上,点A、D是x轴上两点,已知四边形ABCD是正方形,则k=______.
15.(东营)正方形A1B1C1O1,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2)则Bn的坐标是________.
16.点P为直线y=-3x+6上的一点,且点P到两坐标轴距离相等,则P点坐标为_____.
17.已知直线y1=x,y2=x+1,y3=-x+5的图象如图所示,若无论x取何值,y总取y1、y2、y3中最小的值,则y的最大值为_______.
18.已知一次函数y=kx+b的图象经过点P(0,-3),且与函数y=x+1的图象相交于点A().
⑴求a的值;
⑵若函数y=kx+b的图象与x轴的交点是B,函数y=x+1的图象与y轴的交点是C,求四边形ABOC的面积(其中O为坐标原点).
19.定义为一次函数y=px+q的特征数.
⑴求一次函数y=-2(x-1)的特征数;
⑵若特征数是的一次函数为正比例函数,求k的值.
20.已知:三点A(a,1)、B(3,1)、C(6,0),点A在正比例函数y=x的图象上.
⑴求a的值;
⑵点P为x轴上一动点,当△OAP与△CBP周长的和取得最小值时,求点P的坐标;
21.已知直线ln:y=-x+(n是正整数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1.设△A1OB1(O是平面直角坐标系的原点)的面积为s1.当n=2时,直线l2:y=-与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,?…,依次类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
?⑴求△A1OB1的面积s1;
⑵求s1+s2+s3+…+s2010的值.
22.(长沙)在平面直角坐标系中,一动点P(x,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动.图②是P点运动的路程s(个单位)与运动时间t(秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
⑴s与t之间的函数关系式是:_________;
(2)与图③相对应的P点的运动路径是:________;P点出发 _______秒首次到达点B;
⑶写出当3≤s≤8时,y与s之间的函数关系式,并在图③中补全函数图象.
培优升级·奥赛检测
01.已知abc≠0,且=t,则直线y=tx+t一定通过( )
A.第一、二象限 B.第二、三象限 C.第三、四象限 D.第一、四象限
02.一个一次函数的图象与直线y=+平行,与x轴、y轴的交点分别为A、B,并且过点(-1,-25),则在线段AB上(包括端点A、B)横坐标、纵坐标都是整数的点有( )
A.4个 B.5个 C.6个 D.7个
03.在一次函数y=-x+3的图象上取点P,作PA⊥x轴,PB⊥y轴,垂足分别为A、B,长方形OAPB的面积为2,则这样的点P共有( )
A.4个 B.3个 C.2个 D.1个
04.在直角坐标系中,x轴上的动点M(x,0)到定点P(5,5),Q(2,1)的距离分别为MP和MQ,若MP+MQ取最小值,则点M的坐标为________.
05.已知点A(0,2)、B(4,0),点C、D分别在直线x=1与x=2上运动,且CD∥x轴,当AC+CD+DB的值最小值,点C的坐标为_____________.
06.在直角坐标系中,有两个点A(-8,3)、B(-4,5)以及动点C(0,n)、D(m,0).当四边形ABCD的周长最短时,的值为_________.
07.已知函数y=(a-2)x-3a-1,当自变量x的值范围为3≤x≤5时,y既能取到大于5的值,又能取到小于3的值,求实数a的取值范围.
08.(荆州市八年级数学联赛试题)已知一次函数y=ax+b(a为整数)的图象过(98,19),它与x轴的交点为(p,0),与y轴的交点为(0,q),若P为质数,q是正整数,问符合条件的一次函数是否存在?若存在,求出解析式;若存在,说明理由.
09.若直线y=mx-3,y=-1,y=3和x=1所围成的四边形面积为12,求m.
10.设f(x)=kx+1是x的函数,若m(k)表示函数f(x)=kx+1在1≤x≤3条件下的最大值,求函数m(k)的解析式,并作出图象.
第9讲 一次函数与方程、不等式
考点·方法·破译
1. 一次函数与一元一次方程的关系:任何一元一次方程都可以转化成kx+b=0(k、b为常数,k≠0)的形式,可见一元一次方程是一次函数的一个特例.即在y=kx+b中,当y=0时则为一元一次方程.
2. 一次函数与二元一次方程(组)的关系:
⑴任何二元一次方程ax+by=c(a、b、c为常数,且a≠0,b≠0)都可以化为y=的形式,因而每个二元一次方程都对应一个一次函数;
⑵从“数”的角度看,解方程组相当于求两个函数的函数值相等时自变量的取值,以及这个函数值是什么;从“形”的角度看,解方程组相当于确定两个函数图像交点的坐标.
3. 一次函数与一元一次不等式的关系:由于任何一元一次不等式都可以转化成ax+b>0或ax+b<0(a、b为常数,a≠0)的形式,所以解一元一次不等式可以看成是当一次函数的函数值大于或小于0时,求相应自变量的取值范围.
经典·考题·赏析
【例1】直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
A.x>-1 B.x<-1 C.x<-2 D.无法确定
【解法指导】由图象可知l1与l2的交点坐标为(-1,-2),即当x=-1时,两函数的函数值相等;当x>-1时,l2的位置比l1高,因而k2x>k1x+b;当当x<-1时,l1的位置比l2高,因而k2x<k1x+b.因此选A.
【变式题组】
01.(咸宁)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为________.
第1题图 第2题图 第3题图 第4题图
02.(浙江金华)一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
A.0 B.1 C.2 D.3
03. 如图,已知一次函数y=2x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式2x+b>ax-3的解集是________.
04. (武汉)如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式x>kx+b>-2的解集为_________.
【例2】若直线l1:y=x-2与直线l2:y=3-mx在同一平面直角坐标系的交点在第一象限,求m的取值范围.
【解法指导】直线交点坐标在第一象限,即对应方程组的解满足,从而求出m的取值范围.
解:,∴,∵,∴,即,∴-1<m<.
【变式题组】
01. 如果直线y=kx+3与y=3x-2b的交点在x轴上,当k=2时,b等于( )
A.9 B.-3 C. D.
02. 若直线与直线相较于x轴上一点,则直线不经过( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
03. 两条直线y1=ax+b,y2=cx+5,学生甲解出它们的交点坐标为(3,-2),学生乙因抄错了c而解出它们的交点坐标为(,),则这两条直线的解析式为____________.
04. 已知直线y=3x和y=2x+k的交点在第三象限,则k的取值范围是________.
【例3】(四川省初二数学联赛试题)在直角坐标系中,若一点的纵横坐标都是整数,则称该点为整点,设k为整数,当直线y=x-2与y=kx+k的交点为整点时,k的取值可以取( )
A.4个 B.5个 C.6个 D.7个
【解法指导】两直线的交点为整点即对应方程组的解均为整数.
解:由得,
∵两直线交点为整数,
∴x、y均为整数,
又当x为整数时,y为整数,
∴为整数即可,,
∵k-1是整数,
∴k-1=±1,±3时,x、y为整数,
∴k=-2,0,2,4.
所以选A.
【变式题组】
01. (广西南宁)从2,3,4,5这四个数中,任取两个数p和q(p≠q),构成函数y=px-2和y=x+q,并使这两个函数图象的交点在直线x=2的右侧,则这样的有序数对(p,q)共有( )
A.12对 B.6对 C.5对 D.3对
02. (浙江竞赛试题)直线l:y=px(p是不等于0的整数)
考点·方法·破译
1.能够完全重合的两个三角形叫全等三角形.全等三角形的形状和大小完全相同;
2.全等三角形性质:①全等三角形对应边相等,对应角相等;②全等三角形对应高、角平分线、中线相等;③全等三角形对应周长相等,面积相等;
3.全等三角形判定方法有:SAS,ASA,AAS,SSS,对于两个直角三角形全等的判定方法,除上述方法外,还有HL法;
4.证明两个三角形全等的关键,就是证明两个三角形满足判定方法中的三个条件,具体分析步骤是先找出两个三角形中相等的边或角,再根据选定的判定方法,确定还需要证明哪些相等的边或角,再设法对它们进行证明;
5..证明两个三角形全等,根据条件,有时能直接进行证明,有时要证的两个三角形并不全等,这时需要添加辅助线构造全等三角形,构造全等三角形常用的方法有:平移、翻折、旋转、等倍延长线中线、截取等等.
经典·考题·赏析
【例1】如图,AB∥EF∥DC,∠ABC=90°,AB=CD,那么图中有全等三角形( )
A.5对 B.4对 C.3对 D.2对
【解法指导】从题设题设条件出发,首先找到比较明显的一对全等三角形,并由此推出结论作为下面有用的条件,从而推出第二对,第三对全等三角形.这种逐步推进的方法常用到.
解:⑴∵AB∥EF∥DC,∠ABC=90. ∴∠DCB=90.
在△ABC和△DCB中
∴△ABC≌∴△DCB(SAS ) ∴∠A=∠D
⑵在△ABE和△DCE中
∴△ABE≌∴△DCE ∴BE=CE
⑶在Rt△EFB和Rt△EFC中
∴Rt△EFB≌Rt△EFC(HL)故选C.
【变式题组】
01.(天津)下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
02.(丽水)已知命题:如图,点A、D、B、E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.
03.(上海)已知线段AC与BD相交于点O, 连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).
⑴添加条件∠A=∠D,∠OEF=∠OFE,求证:AB=DC;
⑵分别将“∠A=∠D”记为①,“∠OEF=∠OFE”记为②,“AB=DC”记为③,添加①、③,以②为结论构成命题1;添加条件②、③,以①为结论构成命题2.命题1是______命题,命题2是_______命题(选择“真”或“假”填入空格).
【例2】已知AB=DC,AE=DF,CF=FB. 求证:AF=DE.
【解法指导】想证AF=DE,首先要找出AF和DE所在的三角形.AF在△AFB和△AEF中,而DE在△CDE和△DEF中,因而只需证明△ABF≌△DCE或△AEF≌△DFE即可.然后再根据已知条件找出证明它们全等的条件.
证明:∵FB=CE ∴FB+EF=CE+EF,即BE=CF
在△ABE和△DCF中,
∴△ABE≌△DCF(SSS) ∴∠B=∠C
在△ABF和△DCE中, ∴△ABF≌△DCE ∴AF=DE
【变式题组】
01.如图,AD、BE是锐角△ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为( )
A.2 B.3 C.4 D.5
02.如图,在△ABC中,AB=AC,∠BAC=90°,AE是过A点的一条直线,AE⊥CE于E,BD⊥AE于D,DE=4cm,CE=2cm,则BD=__________.
\
03.(北京)已知:如图,在△ABC中,∠ ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过点E作AC的垂线,交CD的延长线于点F. 求证:AB=FC.
【例3】如图①,△ABC≌△DEF,将△ABC和△DEF的顶点B和顶点E重合,把△DEF绕点B顺时针方向旋转,这时AC与DF相交于点O.
⑴当△DEF旋转至如图②位置,点B(E)、C、D在同一直线上时,∠AFD与∠DCA的数量关系是________________;
⑵当△DEF继续旋转至如图③位置时,⑴中的结论成立吗?请说明理由_____________.
【解法指导】⑴∠AFD=∠DCA
⑵∠AFD=∠DCA理由如下:由△ABC≌△DEF,∴AB=DE,BC=EF, ∠ABC=∠DEF, ∠BAC=∠EDF ∴∠ABC-∠FBC=∠DEF-∠CBF, ∴∠ABF=∠DEC
在△ABF和△DEC中,
∴△ABF≌△DEC ∠BAF=∠DEC ∴∠BAC-∠BAF=∠EDF-∠EDC, ∴∠FAC=∠CDF ∵∠AOD=∠FAC+∠AFD=∠CDF+∠DCA
∴∠AFD=∠DCA
【变式题组】
01.(绍兴)如图,D、E分别为△ABC的AC、BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=48°,则∠APD等于( )
A.42° B.48° C.52° D.58°
02.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( )
A.△ABC≌△DEF B.∠DEF=90°
C. AC=DF D.EC=CF
03.一张长方形纸片沿对角线剪开,得到两种三角形纸片,再将这两张三角形纸片摆成如下图形式,使点B、F、C、D在同一条直线上.
⑴求证:AB⊥ED;
⑵若PB=BC,找出图中与此条件有关的一对全等三角形,并证明.
【例4】(第21届江苏竞赛试题)已知,如图,BD、CE分别是△ABC的边A C和AB边上的高,点P在BD的延长线,BP=AC,点Q在CE上,CQ=AB. 求证:⑴ AP=AQ;⑵AP⊥AQ
【解法指导】证明线段或角相等,也就是证线段或角所在的两三角形全等.经观察,证AP=AQ,也就是证△APD和△AQE,或△APB和△QAC全等,由已知条件BP=AC,CQ=AB,应该证△APB≌△QAC,已具备两组边对应相等,于是再证夹角∠1=∠2即可. 证AP⊥AQ,即证∠PAQ=90°,∠PAD+∠QAC=90°就可以.
证明:⑴∵BD、CE分别是△ABC的两边上的高,
∴∠BDA=∠CEA=90°,
∴∠1+∠BAD=90°,∠2+∠BAD=90°,∴∠1=∠2.
在△APB和△QAC中, ∴△APB≌△QAC,
∴AP=AQ
⑵∵△APB≌△QAC,∴∠P=∠CAQ, ∴∠P+∠PAD=90°
∵∠CAQ+∠PAD=90°,∴AP⊥AQ
【变式题组】
01.如图,已知AB=AE,∠B=∠E,BC=ED,点F是CD的中点,求证:AF⊥CD.
02.(湖州市竞赛试题)如图,在一个房间内有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为am,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子顶端距地面的垂直距离NB为bm,梯子倾斜角为45°,这间房子的宽度是( )
A. B. C.bm D.am
03.如图,已知五边形ABCDE中,∠ ABC=∠AED=90°,AB=CD=AE=BC+DE=2,则五边形ABCDE的面积为__________
演练巩固·反馈提高
01.(海南)已知图中的两个三角形全等,则∠α度数是( )
A.72° B.60° C.58° D.50°
02.如图,△ACB≌△A/C/B/,∠ BCB/=30°,则∠ACA/的度数是( )
A.20° B.30° C.35° D.40°
03.(牡丹江)尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA、OB于C、D,再分别以点C、D为圆心,以大于长为半径画弧,两弧交于点P,作射线OP,由作法得△OCP≌△ODP的根据是( )
A.SAS B.ASA C.AAS D.SSS
04.(江西)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A. CB=CD B.∠BAC=∠DAC
C. ∠BCA=∠DCA D.∠B=∠D=90°
05.有两块不同大小的等腰直角三角板△ABC和△BDE,将它们的一个锐角顶点放在一起,将它们的一个锐角顶点放在一起,如图,当A、B、D不在一条直线上时,下面的结论不正确的是( )
A. △ABE≌△CBD B. ∠ABE=∠CBD
C. ∠ABC=∠EBD=45° D. AC∥BE
06.如图,△ABC和共顶点A,AB=AE,∠1=∠2,∠B=∠E. BC交AD于M,DE交AC于N,小华说:“一定有△ABC≌△AED.”小明说:“△ABM≌△AEN.”那么( )
A. 小华、小明都对 B. 小华、小明都不对
C. 小华对、小明不对 D.小华不对、小明对
07.如图,已知AC=EC, BC=CD, AB=ED,如果∠BCA=119°,∠ACD=98°,那么∠ECA的度数是___________.
08.如图,△ABC≌△ADE,BC延长线交DE于F,∠B=25°,∠ACB=105°,∠DAC=10°,则∠DFB的度数为_______.
09.如图,在Rt△ABC中,∠C=90°, DE⊥AB于D, BC=BD. AC=3,那么AE+DE=______
10.如图,BA⊥AC, CD∥AB. BC=DE,且BC⊥DE,若AB=2, CD=6,则AE=_____.
11.如图, AB=CD, AB∥CD. BC=12cm,同时有P、Q两只蚂蚁从点C出发,沿CB方向爬行,P的速度是0.1cm/s, Q的速度是0.2cm/s. 求爬行时间t为多少时,△APB≌△QDC.
12.如图, △ABC中,∠BCA=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
⑴求证:AE=CD;
⑵若AC=12cm, 求BD的长.
13.(吉林)如图,AB=AC,AD⊥BC于点D,AD等于AE,AB平分∠DAE交DE于点F, 请你写出图中三对全等三角形,并选取其中一对加以证明.
14.如图,将等腰直角三角板ABC的直角顶点C放在直线l上,从另两个顶点A、B分别作l的垂线,垂足分别为D、E.
⑴找出图中的全等三角形,并加以证明;
⑵若DE=a,求梯形DABE的面积.(温馨提示:补形法)
15.如图,AC⊥BC, AD⊥BD, AD=BC,CE⊥AB,DF⊥AB,垂足分别是E、F.求证:CE=DF.
16.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,那么在什么情况下,它们会全等?
⑴阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等;
对于这两个三角形均为钝角三角形,可证明它们全等(证明略);
对于这两个三角形均为锐角三角形,它们也全等,可证明如下;
已知△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.求证:△ABC≌△A1B1C1.(请你将下列证明过程补充完整)
⑵归纳与叙述:由⑴可得一个正确结论,请你写出这个结论.
培优升级·奥赛检测
01.如图,在△ABC中,AB=AC,E、F分别是AB、AC上的点,且AE=AF,BF、CE相交于点O,连接AO并延长交BC于点D,则图中全等三角形有( )
A.4对 B.5对 C.6对 D.7对
02.如图,在△ABC中,AB=AC,OC=OD,下列结论中:①∠A=∠B ②DE=CE,③连接DE, 则OE平分∠AOB,正确的是( )
A.①② B.②③ C.①③ D.①②③
03.如图,A在DE上,F在AB上,且AC=CE , ∠1=∠2=∠3, 则DE的长等于()
A.DC B. BC C. AB D.AE+AC
04.下面有四个命题,其中真命题是( )
A.两个三角形有两边及一角对应相等,这两个三角形全等
B.两边和第三边上的高对应相等的两个三角形全等
C. 有一角和一边对应相等的两个直角三角形全等
D. 两边和第三边上的中线对应相等的两个三角形全等
05.在△ABC中,高AD和BE所在直线相交于H点,且BH=AC,则∠ABC=_______.
06.如图,EB交AC于点M, 交FC于点D, AB交FC于点N,∠E=∠F=90°,∠B=∠C, AE=AF. 给出下列结论:①∠1=∠2;②BE=CF; ③△ACN≌△ABM; ④CD=DB,其中正确的结论有___________.(填序号)
07.如图,AD为在△ABC的高,E为AC上一点,BE交AD于点F,且有BF=AC,FD=CD.
⑴求证:BE⊥AC;
⑵若把条件“BF=AC”和结论“BE⊥AC”互换,这个命题成立吗?证明你的判定.
08.如图,D为在△ABC的边BC上一点,且CD=AB,∠BDA=∠BAD,AE是△ABD的中线.求证:AC=2AE.
09.如图,在凸四边形ABCD中,E为△ACD内一点,满足AC=AD,AB=AE, ∠BAE+∠BCE=90°, ∠BAC=∠EAD.求证:∠CED=90°.
10.(沈阳)将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
⑴求证:AF+EF=DE;
⑵若将图①中△DBE绕点B顺时针方向旋转角α,且0°<α<60°,其他条件不变,请在图②中画出变换后的图形,并直接写出(1)中结论是否仍然成立;
⑶若将图①中△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其他条件不变,如图③你认为(1)中结论还成立吗?若成立,写出证明过程;若不成立,请写出此时AF、EF与DE之间的关系,并说明理由。
11.(嵊州市高中提前招生考试)⑴阅读理解:课外兴趣小组活动时,老师提出了如下问题:在△ABC中,AB=5,AC=13, 求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑中线加倍,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
⑵问题解决:受到⑴的启发,请你证明下面命题:如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
求证:BE+CF>EF;
⑶问题拓展:如图,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
12.(北京)如图,已知△ABC.
⑴请你在BC边上分别取两点D、E(BC的中点除外),连接AD、AE,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
⑵请你根据使⑴成立的相应条件,证明:AB+AC>AD+AE.
13.如图,AB=AD,AC=AE,∠BAD=∠CAE=180°. AH⊥AH于H,HA的延长线交DE于G. 求证:GD=GE.
14.已知,四边形ABCD中,AB⊥AD,BC⊥CD,BA=BC,∠ABC=120°,∠MBN=60°, ∠MBN绕B点旋转,它的两边分别交AD、DC(或它们的延长线)于E、F.
当∠MBN绕B点旋转到AE=CF时,如图1,易证:AE+CF=EF;(不需证明)
当∠MBN绕B点旋转到AE≠CF时,如图2和图3中这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,线段AE、CF、EF又有怎样的数量关系?请写出你的猜想,不需证明.
第02讲 角平分线的性质与判定
考点·方法·破译
1.角平分线的性质定理:角平分线上的点到角两边的距离相等.
2.角平分线的判定定理:角的内角到角两边距离相等的点在这个角的平分线上.
3.有角平分线时常常通过下列几种情况构造全等三角形.
经典·考题·赏析
【例1】如图,已知OD平分∠AOB,在OA、OB边上截取OA=OB,PM⊥BD,PN⊥AD.求证:PM=PN
【解法指导】由于PM⊥BD,PN⊥AD.欲证PM=PN只需∠3=∠4,证∠3=∠4,只需∠3和∠4所在的△OBD与△OAD全等即可.
证明:∵OD平分∠AOB ∴∠1=∠2
在△OBD与△OAD中, ∴△OBD≌△OAD
∴∠3=∠4 ∵PM⊥BD,PN⊥AD 所以PM=PN
【变式题组】
01.如图,CP、BP分别平分△ABC的外角∠BCM、∠CBN.求证:点P在∠BAC的平分线上.
02.如图,BD平分∠ABC,AB=BC,点P是BD延长线上的一点,PM⊥AD,PN⊥CD.求证:PM=PN
【例2】(天津竞赛题)如图,已知四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,且AE=(AB+AD),如果∠D=120°,求∠B的度数
【解法指导】由已知∠1=∠2,CE⊥AB,联想到可作CF⊥AD于F,得CE=CF,AF=AE,又由AE=(AB+AD)得DF=EB,于是可证△CFD≌△CEB,则∠B=∠CDF=60°.或者在AE上截取AM=AD从而构造全等三角形.
解:过点C作CF⊥AD于点F.∵AC平分∠BAD,CE⊥AB,点C是AC上一点,
∴CE=CF
在Rt△CFA和Rt△CEA中, ∴Rt△ACF≌Rt△ACE ∴AF=AE
又∵AE=(AE+BE+AF-DF),2AE=AE+AF+BE-DF,∴BE=DF
∵CF⊥AD,CE⊥AB,∴∠F=∠CEB=90°
在△CEB和△CFD中,,∴△CEB≌△CFD
∴∠B=∠CDF 又∵∠ADC=120°,∴∠CDF=60°,即∠B=60°.
【变式题组】
01.如图,在△ABC中,CD平分∠ACB,AC=5,BC=3.求
02.(河北竞赛)在四边形ABCD中,已知AB=a,AD=b.且BC=DC,对角线AC平分∠BAD,问a与b的大小符合什么条件时,有∠B+∠D=180°,请画图并证明你的结论.
【例3】如图,在△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC,CE⊥BE.求证:CE=BD
【解法指导】由于BE平分∠ABC,因而可以考虑过点D作BC的垂线或延长CE从而构造全等三角形.
证明:延长CE交BA的延长线于F,∵∠1=∠2,BE=BE,∠BEF=∠BEC
∴△BEF≌△BEC(ASA) ∴CE=EF,∴CE=CF ∵∠1+∠F=∠3+∠F=90°,
∴∠1=∠3
在△ABD和△ACF中,,∴△ABD≌△ACF
∴BD=CF ∴CE=BD
【变式题组】
01.如图,已知AC∥BD,EA、EB分别平分∠CAB、∠DBA,CD过点E,求证:AB=AC+BD.
02.如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
⑴请你判断FE和FD之间的数量关系,并说明理由;
⑵求证:AE+CD=AC.
演练巩固·反馈提高
01.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于D,若CD=n,AB=m,则△ABD的面积是( )
A.mn B.mn C. mn D.2 mn
02.如图,已知AB=AC,BE=CE,下面四个结论:①BP=CP;②AD⊥BC;③AE平分∠BAC;④∠PBC=∠PCB.其中正确的结论个数有( )个
A. 1 B.2 C.3 D.4
03.如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S.若AQ=PQ,PR=PS,下列结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是( )
A. ①③ B.②③ C.①② D.①②③
04.如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD上任意一点到AB、AC的距离相等;③AD⊥BC且BD=CD;④∠BDE=∠CDF.其中正确的是( )
A.②③ B.②④ C.②③④ D.①②③④
05.如图,在Rt△ABC中,∠ACB=90°,∠CAB=30°,∠ACB的平分线与∠ABC的外角平分线交于E点,则∠AEB的度数为( )
A.50° B.45° C.40° D.35°
06.如图,P是△ABC内一点,PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,且PD=PE=PF,给出下列结论:①AD=AF;②AB+EC=AC+BE;③BC+CF=AB+AF;④点P是△ABC三条角平分线的交点.其中正确的序号是( )
A.①②③④ B.①②③ C.①②④ D.②③④
07.如图,点P是△ABC两个外角平分线的交点,则下列说法中不正确的是( )
A.点P到△ABC三边的距离相等 B.点P在∠ABC的平分线上
C.∠P与∠B的关系是:∠P+∠B=90° D.∠P与∠B的关系是:∠B=∠P
08.如图,BD平分∠ABC,CD平分∠ACE,BD与CD相交于D.给出下列结论:①点D到AB、AC的距离相等;②∠BAC=2∠BDC;③DA=DC;④DB平分∠ADC.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
09.如图,△ABC中,∠C=90°AD是△ABC的角平分线,DE⊥AB于E,下列结论中:①AD平分∠CDE;②∠BAC=∠BDE;③ DE平分∠ADB;④AB=AC+BE.其中正确的个数有( )
A.3个 B.2个 C.1个 D.4个
10.如图,已知BQ是∠ABC的内角平分线,CQ是∠ACB的外角平分线,由Q出发,作点Q到BC、AC和AB的垂线QM、QN和QK,垂足分别为M、N、K,则QM、QN、QK的关系是_________
11.如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC.求证:BE=CF
12.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F.求证:AD⊥EF.
培优升级·奥赛检测
01.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有( )
A.一处 B.二处 C.三处 D.四处
02.已知Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD:CD=9:7,则D到AB边的距离为( )
A.18 B.16 C.14 D.12
03.如图,△ABC中,∠C=90°,AD是△ABC的平分线,有一个动点P从A向B运动.已知:DC=3cm,DB=4cm,AD=8cm.DP的长为x(cm),那么x的范围是__________
04.如图,已知AB∥CD,PE⊥AB,PF⊥BD,PG⊥CD,垂足分别为E、F、G,且PF=PG=PE,则∠BPD=__________
05.如图,已知AB∥CD,O为∠CAB、∠ACD的平分线的交点,OE⊥AC,且OE=2,则两平行线AB、CD间的距离等于__________
06.如图,AD平分∠BAC,EF⊥AD,垂足为P,EF的延长线于BC的延长线相交于点G.求证:∠G=(∠ACB-∠B)
07.如图,在△ABC中,AB>AC,AD是∠BAC的平分线,P为AC上任意一点.求证:AB-AC>DB-DC
08.如图,在△ABC中,∠BAC=60°,∠ACB=40°,P、Q分别在BC、AC上,并且AP、BQ分别为∠BAC、∠ABC的角平分线上.求证:BQ+AQ=AB+BP
第3讲 轴对称及轴对称变换
考点·方法·破译
1.轴对称及其性质
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫对称轴.
轴对称的两个图形有如下性质:①关于某直线对称的两个图形是全等形;②对称轴是任何一对对应点所连线段的垂直平分线;③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.
2.线段垂直平分线
线段垂直平分线也叫线段中垂线,它反映了与线段的两种关系:①位置关系——垂直;②数量关系——平分.
性质定理:线段垂直平分线上的点与这条线段两个端点的距离相等.
判定定理:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
3.当已知条件中出现了等腰三角形、角平分线、高(或垂线)、或求几条折线段的最小值等情况时,通常考虑作轴对称变换,以“补齐”图形,集中条件.
经典·考题·赏析
【例1】(兰州)如图所示,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展开后是( )
【解法指导】对折问题即是轴对称问题,折痕就是对称轴.故选D.
【变式题组】
01.将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是( )
02.(荆州)如图,将矩形纸片ABCD沿虚线EF折叠,使点A落在点G上,点D落在点H上;然后再沿虚线GH折叠,使B落在点E上,点C落在点F上,叠完后,剪一个直径在BC上的半圆,再展开,则展开后的图形为( )
【例2】(襄樊)如图,在边长为1的正方形网格中,将△ABC向右平移两个单位长度得到△A’B’C’,则与点B’关于x轴对称的点的坐标是( )
A.(0,-1) B.(1,1) C.(2,-1) D.(1,-1)
【解法指导】在△ABC中,点B的坐标为(-1,1),将△ABC向右平移两个单位长度得到△A’B’C’,由点的坐标平移规律可得B’(-1+2,1),即B’(1,1).由关于x轴对称的点的坐标的规律可得点B’关于x轴对称的点的坐标是(1,-1),故应选D.
【变式题组】
01.若点P(-2,3)与点Q(a,b)关于x轴对称,则a、b的值分别是( )
A.-2,3 B.2,3 C.-2,-3 D.2,-3
02.在直角坐标系中,已知点P(-3,2),点Q是点P关于x轴的对称点,将点Q向右平移4个单位得到点R,则点R的坐标是___________.
03.(荆州)已知点P(a+1,2a-1)关于x轴的对称点在第一象限,则a的取值范围为___________.
【例3】如图,将一个直角三角形纸片ABC(∠ACB=90°),沿线段CD折叠,使点B落在B1处,若∠ACB1=70°,则∠ACD=( )
A.30° B.20° C.15° D.10°
【解法指导】由折叠知∠BCD=∠B1CD.设∠ACD=x,则∠BCD=∠B1CD=∠ACB1+∠ACD=70°+x.又∠ACD+∠BCD=∠ACB,即x+(70°+x)=90°,故x=10°.故选D.
【变式题组】
01.(东营)如图,把一个长方形纸片沿EF折叠后,点D、C分别落在点D’、C’的位置.若∠EFB=65°,则∠AED’等于( )
A.70° B.65° C.50° D.25°
02.如图,△ABC中,∠A=30°,以BE为边,将此三角形对折,其次,又以BA为边,再一次对折,C点落在BE上,此时∠CDB=82°,则原三角形中∠B=___________.
03.(江苏)⑴观察与发现:小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?请说明理由.
⑵实践与运用:
将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点D’处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.
【例4】如图,在△ABC中,AD为∠BAC的平分线,EF是AD的垂直平分线,E为垂足,EF交BC的延长线于点F,求证:∠B=∠CAF.
【解法指导】∵EF是AD的中垂线,则可得△AEF≌△DEF,∴∠EAF=∠EDF.从而利用角平分线的定义与三角形的外角转化即可.
证明:∵EF是AD的中垂线,∴AE=DE,∠AEF=∠DEF,EF=EF,∴△AEF≌△DEF,∴∠2+∠4=∠3,∴∠3=∠B+∠1,∴∠2+∠4=∠B+∠1,∵∠1=∠2,∴∠B=∠4
【变式题组】
01.如图,点D在△ABC的BC边上,且BC=BD+AD,则点D在__________的垂直平分线上.
02.如图,△ABC中,∠ABC=90°,∠C=15°,DE⊥AC于E,且AE=EC,若AB=3cm,则DC=___________cm.
03.如图,△ABC中,∠BAC=126°,DE、FG分别为AB、AC的垂直平分线,则∠EAG=___________.
04.△ABC中,AB=AC,AB边的垂直平分线交AC于F,若AB=12cm,△BCF的周长为20cm,则△ABC的周长是___________cm.
【例5】(眉山)如图,在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面的备用图中画出所有这样的△DEF.
【解法指导】在正方形格点图中,如果已知条件中没有给对称轴,在找对称轴时,通常找图案居中的水平直线、居中的竖直直线或者斜线作为对称轴.若以图案居中的水平直线为对称轴,所作的△DEF如图①②③所示;若以图案居中的竖直直线为对称轴,所作的△DEF如图④所示;若以图案居中的斜线为对称轴,所作的△DEF如图⑤⑥所示.
【变式题组】
01.(泰州)如图,在2×2的正方形格点图中,有一个以格点为顶点的△ABC,请你找出格点图中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有___________个.
02.(绍兴)如图甲,正方形被划分成16个 全等的三角形,将其中若干个三角形涂黑,且满足下列条件:
⑴涂黑部分的面积是原正方形面积的一半;
⑵涂黑部分成轴对称图形.
如图乙是一种涂法,请在图1-3中分别设计另外三种涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种不同涂法,如图乙与图丙)
【例6】如图,牧童在A处放牛,其家在B处,若牧童从A处出发牵牛到河岸CD处饮水后回家,试问在何处饮水,所求路程最短?
【解法指导】⑴所求问题可转化为CD上取一点M,使其AM+BM为最小;⑵本题利用轴对称知识进行解答.
解:先作点A关于直线CD的对称点A’,连接A’B交CD于点M,则点M为所求,下面证明此时的AM+BM最小.
证明:在CD上任取与M不重合的点M’,
∵AA’关于CD对称,∴CD为线段AA’的中垂线,
∴AM=A’M,M’=A’M’,在△A’M’B中,有A’B<A’M’+BM’,
∴A’M+BM<A’M’+BM’,∴AM+BM<AM’+BM’,
即AM+BM最小.
【变式题组】
01.(山西)设直线l是一条河,P、Q两地相距8千米,P、Q两地到l地距离分别为2千米、5千米,欲在l上的某点M处修建一个水泵站向P、Q两地供水.现在如下四种铺设管道方案,图中的实线表示辅设的管道,则铺设的管道最短的是( )
02.若点A、B是锐角∠MON内两点,请在OM、ON上确定点C、点D,使四边形ABCD周长最小,写出你作图的主要步骤并标明你确定的点.
演练巩固·反馈提高
01.(黄冈)如图,△ABC与△A’B’C’关于直线l对称,且∠A=78°,∠C’=48°,则∠B的度数是( ).
A.48° B.54° C.74° D.78°
02.(泰州)如图,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
03.图1是四边形纸片ABCD,其中∠B=120°,∠D=50°,若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图2所示,则∠C=( )
A.80° B.85° C.95° D.110°
04.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于y轴成轴对称的图形,若点A的坐标是(1,3),则点M和点N的坐标分别是( )
A.M(1,-3),N(-1,-3) B.M(-1,-3),N(-1,3)
C.M(-1,-3),N(1,-3) D.M(-1,3),N(1,-3)
05.点P关于x轴对称的对称点P’的坐标是(-3,5),则点P关于y轴对称的对称点的坐标是( )
A.(3,-5) B.(-5,3) C.(3,5) D.(5,3)
06.已知M(1-a,2a+2)关于y轴对称的点在第二象限,则a的取值范围是( )
A.-1<a<1 B.-1≤a≤1 C.a>1 D.a>-1
07.(杭州)如图,镜子中号码的实际号码是___________.
08.(贵阳)如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为___________cm2.
09.已知点A(2a+3b,-2)和B(8,3a+2b)关于x轴对称,则a+b=___________.
10.如图,在△ABC中,OE、OF分别是AB、AC中垂线,且∠ABO=20°,∠ABC=45°,求∠BAC和∠ACB的度数.
11.如图,C、D、E、F是一个长方形台球桌的4个顶点,A、B是桌面上的两个球,怎样击打A球,才能使A球撞击桌面边缘CF后反弹能够撞击B球?请画出A球经过的路线,并写出作法.
12.如图,P为∠ABC的平分线与AC的垂直平分线的交点,PM⊥BC于M,PN⊥BA的延长线于N.求证:AN=MC.
13.(荆州)有如图“”的8张纸条,用每4张拼成一个正方形图案,拼成的正方形的每一行和每一列中,同色的小正方形仅为2个 ,且使每个正方形图案都是轴对称图形,在网格中画出你拼成的图.(画出的两个图案不能全等)
培优升级·奥赛检测
01.(浙江竞赛试题)如图,直线l1与直线l2相交,∠α=60°,点P在∠α内(不在l1l2上).小明用下面的方法作P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作P1关于l2的对称点P2,然后再以l1为对称轴作P2关于l1的对称点P3,以l2为对称轴作P3关于l2的对称点P4,……如此继续,得到一系列P1、P2、P3……Pn与P重合,则n的最小值是( )
A.5 B.6 C.7 D.8
02.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
⑴如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
⑵如果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是点P1,点P1关于直线l的对称点是P2,求PP2的长.
03.(荆州)某住宅小区拟栽种12棵风景树,若想栽成6行,每行4棵,且6行树所处位置连成线后能组成精美的对称图案,请你仿照举例在下面方框中再设计两种不同的栽树方案.
04.(宜昌)已知:如图,AF平分∠BAC,BC⊥AF,垂足为E,点D与点A关于点E对称,PB分别与线段CF、AF相交于P、M.
⑴求证:AB=CD;
⑵若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
05.在△ABC中,∠BAC=90°,点A关于BC边的对称点为A’,点B关于AC边的对称点为B’,点C关于AB边的对称点为C’,若S△ABC=1,求S△A’B’C’.
06.(湖州市竞赛试题)小王同学在小组数学活动中,给本小组出了这样一道“对称跳棋”题:如图,在作业本上画一条直线l,在直线l两边各放一粒围棋子A、B,使线段AB长a厘米,并关于直线l对称,在图中P1处有一粒跳棋子,P1距A点b厘米、与直线l的距离C厘米,按以下程序起跳:第1次,从P1点以A为对称中心跳至P2点;第2次,从P2点以l为对称轴跳至P3点;第3次,从P3点以B为对称中心跳至P4点;第4次,从P4以l为对称轴跳至P1点;
⑴画出跳棋子这4次跳过的路径并标注出各点字母;(画图工具不限)
⑵棋子按上述程序跳跃2011次后停下,假设a=8,b=6,c=3,计算这时它与A的距离是多少?
07.(湖州)如图,已知平面直角坐标系,A、B两点的坐标分别为A(2,-3),B(4,-1).
⑴若P(p,0)是x轴上的一个动点,则当p=___________时,△PAB的周长最短;
⑵若C(a,0),D(a+3,0)是x轴上的两个动点,则当a=___________时 ,四边形ABCD的周长最短;
⑶设M、N分别为x轴和y轴上的动点,请问:是否存在这样的点M(m,0)、N(0,n),使四边形ABMN的周长最短?若存在,请求出m=___________,n=___________(不必写解答过程);若不存在,请说明理由.
第4讲 等腰三角形
考点·方法·破译
1.等腰三角形及其性质
有两条边相等的三角形叫做等腰三角形,等腰三角形是轴对称图形,因此它的性质有:⑴等腰三角形的两个底角相等(即等边对等角);⑵等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(即等腰三角形三线合一)
2.等腰三角形的判定
证明一个三角形是等腰三角形的基本方法是:⑴从定义入手,证明一个三角形有两条边相等;⑵从角入手,证明一个三角形有两个角相等,依据是等腰三角形判定定理;等角对等边.
3.构造等腰三角形的常用方法
⑴角平分线+平行线=等腰三角形 ⑵角平分线+垂线(或高)=等腰三角形
⑶线段中垂线构造等腰三角形 ⑷将2倍角转化为相等角构造等腰三角形
经典·考题·赏析
等腰三角形一腰上的高与另一腰所成的夹角为400,则这个等腰三角形的底角为________________.
【解法指导】 若问题中涉及到三角形的高,则要分别考虑三角形的高是在三角形的外,三角形内的情况.
解:如图1,当一腰上的高在三角形内时,∠ACD=400,∴∠A=500
∴∠B=∠ACB=
如图2,当一腰上的高在三角形外时,∠ACD=400,∠DAC=500
∴∠DAC=∠B+∠ACB=2∠B
∴∠B=∠ACB=250,故填650或250.
【变式题组】
01.(呼和浩特)在等腰⊿ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )
A.7 B.11 C.7或11 D.7或10
02.(黄冈)在⊿ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为500,则∠B=___________度.
03.(襄樊)在⊿ABC中,AB=AC=12cm,BC=6cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的方向运动.设运动时间为t,那么当t=_________秒时,过D、P两点的直线将⊿ABC的周长分成两个部分,使其中一部分是另一部分的2倍.
【例2】 如图,在⊿ABC中,AB=AC,点D在AC上,AD=BD=BC,求∠A的度数.
【解法指导】 图中的等腰三角形多,可利用等腰三角形的性质,用方程的思想求角的度数.
解:设∠A=x,
∵BD=AD,∴∠A=∠ABD=x,
∴∠BDC=∠A+∠ABD=2x,
∵BD=BC,∴∠C=∠BDC=2x,
∵AB=AC,∴∠ C=∠ABC=2x,
∵在△ABC中, ∠A+∠ABC+∠ACB=180°
∴x+2x+2x=180°,
x=36°,∴∠A=36°.
【变式题组】
01.如图,在⊿ABC中,AB=AC,BD=BC,AD=DE=EB,求∠A的度数.
02.如图,在⊿ABC中,AB=AC,BC=BD= ED=EA,求∠A的大小.
【例3】 已知坐标原点O和点A(2,-2),B是坐标轴上的一点.若⊿AOB是等腰三角形,则这样的点B一共有( )个
A.4 B.5 C.6 D.8
【解法指导】 ⊿AOB是等腰三角形,但不能确定哪条边是等腰三角形的底,因而要分三种情况进行说明①AO=OB,②OA=AB,③BA=BO,又∵B是坐标轴上的点.要考虑x轴与y轴两种情况.
解:①如图1,当OA是底边时,B在OA的中垂线上,又B在坐标轴上,因而B是OA中垂线与坐标轴的交点;
②如图2,当OA为腰时,若O为顶点,则B在以O为圆心,OA为半径的圆上,又B在坐标轴上,因而B是圆与坐标轴的交点;
③如图3,当OA为腰时,若A为顶点,则B在以A为圆心,OA为半径的圆上,又B在坐标轴上,因而B是圆与坐标轴的交点.故选D.
【变式题组】
01.(海南竞赛试题)在平面直角坐标系xOy内,已知A(3,-3),点P是y轴上一点,则使⊿AOP为等腰三角形的点P共有( )
A.2个 B.3个 C.4个 D.5个
02.如图,在平面直角坐标系中,点A的坐标是(1,0),点B的坐标是(0,),点C在坐标平面内.若以A、B、C为顶点构成的三角形是等腰三角形,且底角为30度,则满足条件的点C有_________个.
03.(南昌)如图,已知长方形纸片ABCD,点E是AB的中点,点G是BC上一点,∠BEG>600,现沿直线EG将纸片折叠,使点B落在纸片中的点H处,连接AH,则与∠BEG相等的角的个数为( )
A.4 B.3 C.2 D.1
04.(济南)如图所示,矩形ABCD中,AB=4,BC=,点E是折线段A-D-C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
A.2个 B.3个 C.4个 D.5个
【例4】 (枣庄)两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连结BD,取BD的中点M,连结ME,MC.试判断△EMC的形状,并说明理由.
【解法指导】 判断⊿MEC为等腰直角三角形,M为直角顶点,即想证∠EMC=900,而⊿ABD为等腰三角形,M是BD的中点,若连接AM则有∠AMD=900,因而只需证∠DME=∠AMC,利用全等三角形即可.
解:的形状是等腰直角三角形,理由如下:
连接,由题意得:
.
.
又,
.
.
.
.
又,
.
.
所以的形状是等腰直角三角形.
【变式题组】
01.如图,在等腰直角三角形ABC中,P是斜边BC的中点,以P为直角顶点的两边分别与边AB、AC交于点E、F,当∠EPF绕顶点P旋转时(点E不与A、B重合),⊿PEF也始终是等腰三角形,请你说明理由.
02.如图,在等腰三角形ABC中,∠ACB=900,D是BC的中点,DE⊥AB垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF交AD于G.
⑴求证:AD⊥CF;
⑵连接AF,试判断⊿ACF的形状,并说明理由.
03.如图,⊿ABC中,∠ACB=900,AC=BC,CO为中线.现将一直角三角板顶点放在点O上并绕点O旋转,若三角板的两直角边分别交AC、CB的延长线于点G、H.
⑴试写出图中除AC=BC,OA=OB=OC外其他所有相等的线段;
⑵请选一组你写出的相等线段给予证明.
【例5】 我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
⑴请写出一个你学过的特殊四边形中是等对边四边形的图形的名称;
⑵如图,在中,点分别在上,设相交于点,若,.请你写出图中一个与相等的角,并猜想图中哪个四边形是等对边四边形;
⑶在中,如果是不等于的锐角,点分别在上,且.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
【解法指导】 证明两条线段相等时,若两条线段在同一三角形中,可证明它们所对的角相等.若两条线段在不同的三角形中,则证它们所在的两个三角形全等,若三角形不全等,即可通过构造全等三角形或等腰三角形解决问题.
解:⑴如:平行四边形、等腰梯形等
⑵答:与∠A相等的角是∠BOD(或∠COE),四边形DBCE是等对边四边形;
⑶答:此时存在等对边四边形,是四边形DBCE.
证法一:如图1,作CG⊥BE于G点,作BF⊥CD交CD延长线于F点.
∵∠DCB=∠EBC=∠A,BC为公共边,
∴△BCF≌△CBG,
∴BF=CG,
∵∠BDF=∠ABE+∠EBC+∠DCB,∠BEC=∠ABE+∠A,
∴∠BDF=∠BEC,
可证△BDF≌△CEG,
∴BD=CE
∴四边形DBCE是等边四边形.
证法二:如图2,以C为顶点作∠FCB=∠DBC,CF交BE于F点.
∵∠DCB=∠EBC=∠A,BC为公共边,
∴△BDC≌△CFB,
∴BD=CF,∠BDC=∠CFB,
∴∠ADC=∠CFE,
∵∠ADC=∠DCB+∠EBC+∠ABE,∠FEC=∠A+∠ABE,
∴∠ADC=∠FEC,
∴∠FEC=∠CFE,
∴CF=CE,∴BD=CE,
∴四边形DBCE是等边四边形.
【变式题组】
01.如图,在ABC中,∠B=2∠C,AD为∠BAC的平分线.求证:AC=AB+BD.
02.(天津初赛试题)如图,在四边形ABCD中,∠ACB=∠BAD=1050,∠ABC=∠ADC=450,若AB=2,求CD的长.
03.如图,在ABC中,AB=AC,D在AB上,F在AC延长线上,BD=CF.求证DE=EF.
【变式题组】
01.(重庆)已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为( )
A.200 B.1200 C.200或1200 D.3600
02.(云南)已知等腰三角形的两边分别为6和3,则此等腰三角形周长为( )
A.9 B.15 C.15 D.12或15
03.(云南)如图,等腰ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则BEC的周长为( )
A.13 B.14 C.15 D.16
04.如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=180,则∠GEF的度数是( )
A.800 B.900 C.1000 D.1080
05.如图,RtABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中不正确的是( )
A.∠ACD=∠B B.CH=CE=EF C.CH=HD D.AC=AF
06.如图,ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①BDF和CEF都是等腰三角形;②DE=BD+CE;③ADE的周长等于AB与AC的和;④BF=CF.其中正确的有( )
A.①②③ B.①②③④ C.①② D.①
07.(武汉)如图,已知O是四边形ABCD内一点,OA=OB=OC, ∠ABC=∠ADC=700,则∠DAO+∠DCO的大小是( )
A.700 B.1100 C.1400 D.1500
08.(滨州)已知等腰ABC的周长为10,若设腰长为x,则x的取值范围是____________.
09.如图所示,在ABC中,已知AB=AC,∠A=360,BC=2,BD是ABC的角平分线,则AD=___________.
10.(威海)如图,AB=AC,BD=BC,若∠A=400,则∠ABD的度数是_________.
11.(乌鲁木齐) 在一次数学课上,王老师在黑板上画出图6,并写下了四个等式:
①,②,③,④.
要求同学从这四个等式中选出两个作为条件,推出是等腰三角形.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)
已知:
求证:是等腰三角形.
证明:
12.(泰安) 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,在同一条直线上,连结.
⑴请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
⑵证明:.
13.(包头)如图,已知中,厘米,厘米,点为的中点.
⑴如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?
⑵若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?
14.(临沂)如图1,已知中,,,把一块含角的直角三角板的直角顶点放在的中点上(直角三角板的短直角边为,长直角边为),将直角三角板绕点按逆时针方向旋转.
⑴在图1中,交于,交于.
①证明;
②在这一旋转过程中,直角三角板与的重叠部分为四边形,请说明四边形的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
⑵继续旋转至如图2的位置,延长交于,延长交于,是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
⑶继续旋转至如图3的位置,延长交于,延长交于,是否仍然成立?请写出结论,不用证明.
培优升级·奥赛检测
01.如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:①GA=GP;②③BP垂直平分CE;④FP=FC;其中正确的判断有( )
A.只有①② B.只有③④ C.只有①③④ D.只有①②③④
02.如图,点A是网格图形中的一个网格图形中的一个格点(小正方形的顶点),图中每个小正方形的边长为1,以A为其中的一个顶点,面积等于2.5的格点等腰直角三角形(三角形的三个顶点都是格点)的个数是( )
A.10个 B.12个 C.14个 D.16个
03.如图,在ABC中,AB=BC,MN=NA, ∠BAM=∠NAC,则∠MAC=_________.
04.如图,AA’、BB’分别是∠EAB、∠DBC的平分线,若AA’=BB’=AB.则∠BAC的度数为______________.
05.(全国联赛)在等腰RtABC中,AC=BC=1,M是BC的中点,CE⊥AM于E,交AB于F.则 =_____________
06.如图,在ABC中,AB=AC,EF为过点A的任意一条直线,CF⊥BC, BE⊥BC.求证:AE=AF.
07.(湖州市竞赛试题)如图,在RtABC中,∠ACB=900,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE,求证:FK∥AB
08.(四川省初二数学联赛试题)有一等腰钝角三角形纸片,若能从一个顶点出发,将其剪成两个等腰三角形纸片,求等腰三角形纸片的顶角的度数.
09.如图,在ABC中,∠ABC=460,D是边BC上一点,DC=AB, ∠DAB=210,求∠CAD的度数.
10.(浙江省杭州市中考试题)如图,在等腰△中,是底边上的高线,点是线段上不与端点重合的任意一点,连接交于点,连接交于点.
(1) 证明:;
(2) 证明:;
(3) 以线段和为边构成一个新的三角形(点与点重合于点),记△和△的面积分别为和,如果存在点,能使得 , 求∠的取值范围.
11.如图,已知在△中,AB=AC,∠BAC=900,AD=AE, AF⊥BE交BC于F,过F作FG⊥CD交BE的延长线于G.求证:BG=AF+FG
第五讲 等边三角形
考点 方法 破译
1.等边三角形及其性质:三边都相等的三角形叫做等边三角形,等边三角形的三个内角都相等,并且每一个角都等于60.等边三角形是轴对称图形,对称轴是顶角平分线或底边上的高、中线所在直线;
2.等边三角形的判定:三边都相等的三角形是等边三角形;三个角都相等的三角形是等边三角形;有一个角为60°的等腰三角形是等边三角形;
3.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,反之也成立.
经典 考题 赏析
【例1】如图,△DAC和△EBC均是等边三角形,A、C、B三点在一条直线上.AE、BD分别与CD、CE交于点M、N.
(1)求证:△ACE≌△DCB;
(2)求∠AFD的度数;
(3)判断△CMN的形状
【解法指导】根据等边三角形的性质,利用全等三角形中边角的关系可解决问题.
解:(1)∵等边三角形DAC与等边三角形EBC ∴AC=DC,CE=CB,∠ACD=∠BCE=60°
∴ ∠ACE=∠DCB
∴在△ACE和△DCB中,,∴△ACE≌△DCB
(2) ∵∠ACE≌∠DCB, ∴∠1=∠2
又∵∠1+∠DFA==∠2+∠ACD ∴∠AFD=∠ACD=60°
(3) 在△ACM和△DCN中,
∴△ACM≌△DCN ∴CM=CN
又∵∠DCN =60°∴△CMN是等边三角形.
【变式题组】
01.(天津)如图,P、Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,
则∠BAC的大小等于__________ 度
02.(荆州)如图,D是等边△ABC的边AB上的一动点,以CD为一边向上作等边△EDC,连接AE,找出图中的一组全等三角形,并说明理由.
03.如图,在正△ABC中,D,E分别是BC、AC上的一点,且AE=CD .AD与BE相交于点P,且BQ⊥AD于Q.求证BP=2PQ
04.(黄冈)如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q是BC延长线上一点,当PA=CQ时,连接PQ交AC于D,求DE的长.
【例2】P是△ABC内一点,∠PBC=30°,∠PBA=8°,且∠PAB=∠PAC=22°,求∠APC的度数
【解法指导】 由于∠PAB =∠PAC,因而PA平分∠BAC,根据角平分线的特点可构造全等三角形,其方法一:在AB边上截取;方法二:延长AC边,又由于∠BPA=150°是特殊角,考虑∠BPA的完整性,因而取方法二的可能性更大.
解:延长AC到D,使AD=AB,连接PD、BD,∵∠PBA=8°∠PAB =22°
∴∠BPA=150°,在△ABP和△ADP中,∴△ABP≌△ADP ∴∠APB=∠APD = 150°,BP=DP ,∠PBA=∠APD =8°
∴∠BPD=60°, ∴△BPD是正三角形
∵∠PBC=30° ∴∠PBC=∠DBC
在△PBC和△DBC中,
∴△PBC≌△DBC , ∴PC=CD ∴∠CPD=∠CDP=8°
∴∠APC=∠APD一∠CPD=150°一8°=142°
【变式题组】
01.如图,D是等边三角形ABC内一点,E为ABC外部一点,满足DA=DB,BE=BA,∠DBE=∠DBC.求∠BED的度数.
02.如图.D是△ABC外一点.AB=AC=BD+CD,∠ABD=60°求∠ACD的度数.
【例3】如图(1),△ABC等边三角形,△BDC是顶角120°的等腰三角形,以D为顶点作60°的角,它的两边分别与AB、AC交于点M和N,连接MN.
(1)探究:MN、NC之间的关系,并加以证明;
(2)若点M、N分别在射线AB、CA上,其他条件不变,再探究线段BM、MN、NC之间的关系,在图(2)中画出相应的图形.并就结论说明理由
【解法指导】对于(1),这时在△DMB中,有∠DBM=∠DBC+∠CBA=30°+60°=90°
为了把BM,MN,NC集中到一个三角形中去,将△DMB 绕D点顺时针旋转120°得到△DGC.如图(3).从而有MB=GC.而此时恰又有△MND≌△GND·得MN=NG=NC+CG=NC+BM.对于(2),此时的图形(4),仍作(1)中的旋转,类似地可以推得MN=CN一BM
解(1)关系为MN=BM+NC
证明:延长AC到G,使CG=BM,连接DG,如图(3)
∠ABD=∠ABC+∠CBD=60°十30°=90°同理也有∠ACD=90°
在△DMB和△DGC中; DB=DC.BM=CG
∴△DMB≌△DGC ∴DM=DG.∠MDB=∠GDC.
在△MND和△GND中,ND公用,DM=DG,∠MDN=60°
∠GDN=∠GDC+∠DCN=∠MDB+∠CDN=60°
∴△MND≌△GND ∴ MN=GN=GC十NC=BM+NC
(2)此时.图形如图(4),有关系式MN=CN—BM理由如下:
在CN上截取GG=BM.连接DG,如图(4)与(1)中情况类似.可推得
∠ABD=∠ACD=90°.且Rt△DMB≌△DGC ,得DM=DG.∠MDB=∠GDC
仍与(1)中情况娄似,可推得△MND≌△GND.就有MN=GN=NC—CG=NC—BM.
【变式题组】
01.用两个全等的等边三角形△ABC和△ACD拼成四边形ABCD,把一个含60°角的三角尺与这个四边形叠合,使三角尺的60°角的顶点与点A重合.两边分别与AB、AC重合,将三角尺绕点A按逆时针方向旋转
(1)当三角尺的两边分别与四边形的两边BC、CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;
(2)当三角尺的两边分别与四边形的两边BC、CD的延长线相交于点F时(如图2),你在(1)中得到的结论还成立吗,简要说明理由.
02.如图.四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°
求证:AC=BC+DC.
巩固练习 反馈提高
01.如图.△ABC是等边三角形,AD⊥BC,点E在AC上,且AE=AD,则∠DEC=( )
A 105° B 85° C 95° D 75°
第1题图 第2题图
02.如图,等边△ABC,D在AC上,延长BC到E.使CE=CD,若BD=DE,给出下列结论:① BD平分∠ABC ② AD = AB ③ CE= BC ④∠A=2∠E,其中正确结论的个数是( )
A.4个 B 3个 C 2个 D 1个
03.(河北)如图,等边△ABC的边长为1cm,D、E分别是AB、AC 上的点,将△ABC沿直线DE折叠,点A落在A’处,且A’在△ABC外部,则阴影部分图形的周长为__________ cm
04.在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°,得到线段OD,要使点D恰好落在BC上,则AP=__________.
05.如图,△ABC是等边三角形,D、E、F分别在AB、BC、AC上,且DE⊥BC,EF⊥AC,FD⊥AB,试判断△DEF是否为等边三角形,并说明理由.
06.请你用三种不同的分割方法,将图中的三个正三角形分别分割成四个等腰三角形(在图中画出分割线,并标出必要的角的度数) .
07.如图,点D是等边△ABC边AB上的一点.AB=3AD,DE⊥BC于点E,AE、CD相交于点F
(1)求证:△ACD≌△BAE:
(2)过点C作CG⊥AE,垂足为点G,探究CF与FG之间的数量关系,并证明.
08.如图:△ABC是等边三角形,D是AB边上的点,将线段DB绕点D顺时针旋转60°得到线段DE,延长ED交AC于点F,连接DC,AE.
求证:△ADE≌△DFC
09.如图:△ABC是等边三角形,点D、E分别在CA、AB的延长线上, AD=BE.DB的延长线交EC于F.
求证:(1)DB=EC;(2) ∠BFC=60°
10.(常德)如图1,若△ABC与△ADE为等边三角形,M、N分别是EB、CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕点A旋转到图2的位置时,CD=BE是否仍然成立? 若成立请证明,若不成立请说明理由;
(2) 当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形? 若成立请证明,若不成立请说明理由.
第06讲 实 数
考点·方法·破译
1.平方根与立方根:
若=a(a≥0)则x叫做a的平方根,记为:a的平方根为x=±,其中a的平方根为x=叫做a的算术平方根.
若x3=a,则x叫做a的立方根.记为:a的立方根为x=.
2.无限不循环小数叫做无理数,有理数和无理数统称实数.实数与数轴上的点一一对应.任何有理数都可以表示为分数(p、q是两个互质的整数,且q≠0)的形式.
3非负数:
实数的绝对值,实数的偶次幂,非负数的算术平方根(或偶次方根)都是非负数.即>0,≥0(n为正整数),≥0(a≥0) .
经典·考题·赏析
【例1】若2m-4与3m-1是同一个数的平方根,求m的值.
【解法指导】一个正数的平方根有两个,并且这两个数互为相反数.∵2m ?4与3m?l是同一个数的平方根,∴2m?4 +3m?l=0,5m=5,m=l.
【变式题组】
01.一个数的立方根与它的算术平方根相等,则这个数是____.
02.已知m是小于的最大整数,则m的平方根是____.
03.的立方根是____.
04.如图,有一个数值转化器,当输入的x为64时,输出的y是____.
【例2】(全国竞赛)已知非零实数a、b满足,则a+b等于( )
A.-1 B. 0 C.1 D.2
【解法指导】若有意义,∵a、b为非零实数,∴b2>0∴a-3≥0 a≥3
∵
∴,∴.
∴,∴,故选C.
【变式题组】
0l.在实数范围内,等式=0成立,则ab=____.
02.若,则的平方根是____.
03.(天津)若x、y为实数,且,则的值为( )
A.1 B.-1 C.2 D.-2
04.已知x是实数,则的值是( )
A. B. C. D.无法确定
【例3】若a、b都为有理效,且满足.求a+b的平方根.
【解法指导】任何两个有理数的和、差、积、商(除数不为0)还是有理数,但两个无理数的和、差、积、商(除数不为0)不一定是无理数.∵,
∴ 即,∴,
a +b=12 +13=25.
∴a+b的平方根为:.
【变式题组】
01.(西安市竞赛题)已知m、n是有理数,且(+2)m+(3-2)n+7=0求m、n.
02.(希望杯试题)设x、y都是有理数,且满足方程()x+()y?4?=0,则x?y=____.
【例4】若a为?2的整数部分,b?1是9的平方根,且,求a+b的值.
【解法指导】一个实数由小数部分与整数部分组成,?2=整数部分+小数部分.整数部分估算可得2,则小数部分=?2 ?2=?4.∵a=2,b?1=±3 ,∴b=-2或4
∵.∴a【变式题组】
01.若3+的小数部分是a,3?的小数部分是b,则a+b的值为____.
02.的整数部分为a,小数部分为b,则(+a)·b=____.
演练巩固 反馈提高
0l.下列说法正确的是( )
A.-2是(-2)2的算术平方根 B.3是-9的算术平方根
C. 16的平方根是±4 D.27的立方根是±3
02.设,b= -2,,则a、b、c的大小关系是( )
A.a
A.-9与81的平方根 B.4与 C.4与 D.3与
04.在实数1.414,,0.,5?,,3.,中无理数有( )
A.2个 B.3个 C.4个 D. 5个
05.实数a、b在数轴上表示的位置如图所示,则( )
A.b>a B.
C. -a<b D.-b>a
06.现有四个无理数,,,,其中在+1与+1之间的有( )
A. 1个 B.2个 C. 3个 D .4个
07.设m是的平方根,n=.则m,n的关系是( )
A. m=±n B.m=n C .m=-n D.
08.(烟台)如图,数轴上 A、B两点表示的数分别为-1和,点B关于点A的对称点C,则点C所表示的数为( )
A.-2 B.-1 C.-2 + D.l +
09.点A在数轴上和原点相距个单位,点B在数轴上和原点相距3个单位,且点B在点A左边,则A、B之间的距离为____.
10.用计算器探索:已知按一定规律排列的一组数:1,,…,,.如果从中选出若干个数,使它的和大于3,那么至少要选____个数.
11.对于任意不相等的两个数a、b,定义一种运算※如下:a※b=,如3※2==.那么12.※4=____.
12.(长沙中考题)已知a、b为两个连续整数,且a<
14.设a是大于1的实数.若a,,在数轴上对应的点分别是A、B、C,则三点在数轴上从左自右的顺序是____.
15.如图,直径为1的圆与数轴有唯一的公共点P.点P表示的实数为-1.如果该圆沿数轴正方向滚动一周后与数轴的公共点为P′,那么点P′所表示的数是____.
16.已知整数x、y满足+2=,求x、y.
17.已知2a?1的平方根是±3,3a+b?1的算术平方根是4,求a+b+1的立方根.
18.小颖同学在电脑上做扇形滚动的游戏,如图有一圆心角为60°,半径为1个单位长的扇形放置在数轴上,当扇形在数轴上做无滑动的滚动时,当B点恰好落在数轴上时,(1)求此时B点所对的数;(2)求圆心O移动的路程.
19.若b= + +3l,且a+11的算术平方根为m,4b+1的立方根为n,求(mn?2)(3mn +4)的平方根与立方根.
20.若x、y为实数,且(x?y+1)2与互为相反数,求的值.
培优升级 奥赛检测
01.(荆州市八年级数学联赛试题)一个正数x的两个平方根分别是a+1与a?3,则a值为( )
A. 2 B.-1 C. 1 D. 0
02.(黄冈竞赛)代数式++的最小值是( )
A.0 B. 1+ C.1 D. 2
03.代数式?2的最小值为____.
04.设a、b为有理数,且a、b满足等式a2+3b+b=21?5,则a+b=____.
05.若=1,且3=4,则在数轴上表示a、b两数对应点的距离为____.
06.已知实数a满足,则a? 20092=_______.
07.若m满足关系式 ,试确定m的值.
08.(全国联赛)若a、b满足=7,S=,求S的取值范围.
09.(北京市初二年级竞赛试题)已知0
11.(全国竞赛试题)巳知x=,a、b为互质的正整数.且a≤8,?1
第7讲 变量与函数
考点·方法·破译
1.函数的概念及其表示方法
⑴函数的定义:在一个变化过程中,有两个变量x和y,对于给定的每一个x值,y都有唯一确定的值与其对应,那么,x是自变量,y是x的函数.
⑵函数的表示方法
①解析法:用含有自变量的代数式表示函数的方法;
②列表法:把自变量x的一系列值和函数y的对应值列成表格来表示函数的方法;
③图象法:用图象表示函数关系的方法.
2.自变量取值范围的确定
自变量的取值必须使含自变量的代数式都有意义,且必须符合实际问题的要求.
经典·考题·赏析
【例1】(兰州)函数中自变量x的取值范围是( )
A. x≤2 B. x=3 C. x<2且x≠3 D.x≤2且x≠3
【解法指导】 求x的取值范围,可根据题目要求列出下列式子: 解得x≤2且x≠3, 故选A
【变式题组】
01.(大兴安岭)函数中,自变量x 的取值范围是________
02.(芜湖)函数中自变量x的取值范围是_________
03.函数中自变量x的取值范围是_________
04.已知函数y=-2x+1中的自变量x的取值范围是0<x<10,则y的取值范围是______
【例2】汽车由北京驶往相距850km的沈阳,它的平均速度为80km/h,求汽车距沈阳的路程s(km)与行驶时间t(h)的函数关系式,写出自变量的取值范围
【解法指导】⑴此题属于行程问题,其基本数量关系是:速度时间=路程.因此汽车行驶t(h)的路程是80t(km)与汽车距沈阳的路程s(km)及北京与沈阳的距离850km之间的等量关系是80t+s=850;(2)由于s与t都应是非负数可确定自变量的取值范围.
解:由题意得,s=850-80t
又由于 即 解得 0≤t≤
因此汽车距沈阳的路程s与时间t的函数关系式为s=850-80t,自变量的取值范围是0≤t≤
【变式题组】
01.已知三角形的面积为20cm2,设它的底边长为x(cm),则底边上的高y(cm)关于x的函数关系式为______,自变量的取值范围是__________.
02.等腰三角形的周长是40cm,腰长y(cm)与底边长x(cm)关系的函数解析式正确的是( )
A. y=-0.5x+20(0<x<20) B.y=-0.5x+20(10<x<20)
C. y=-2x+40(10<x<20) D.y=-2x+40(0<x<20)
03. 某市为了鼓劲居民节约用水,对自来水用户按如下标准收费:若每月每户用水不超过12米3,按每立方米 a 元收费;若超过12米3,则超过部分每立方米按2a元收费.某户居民五月份交水费y(元)与用水量x(米3)(x>12)之间的关系式为______,若该月交水费20a元,则这个月实际用水______米3.
【例3】下列曲线中,表示y不是x的函数的是( )
【解法指导】 要根据曲线判断所给变化中,y是否是x的函数,则需要根据曲线观察对于x的每一个确定的值,是否y都有惟一的一个确定的值与之对应,如果是,则y就是x的函数,观察所给的四个选项,可知B中所示的曲线,当x取一个值时,y有两个值与之对应,根据函数的定义可知y不是x的函数,应选B.
【变式题组】
01.图中分给给出了x与y的对应关系,其中y是x的函数是( )
02.下列函数中,与y=x表示同一个函数的是( )
A. B. C. D.
【例4】 如右图,圆柱形开口杯的底部固定在长方体池底,向水池匀速注入水(倒在杯外),水池中水面高度是h ,注水时间是t,则h与t之间的关系大致为下面图中的( )
【解法指导】由题意知,此注水过程中分为三段:⑴由于圆柱形开口杯底部固定在长方体水池,也就是说水池被开口杯占据了一部分空间,因此注水时水池中水面上升的速度较快,其图象是一段自原点出发较陡的上升线段;⑵当水的与开口杯口等高时,水开始注入开口杯,也就是说水池中水面高度不变,则其图象是一段平行于t轴的水平线段;⑶当开口杯注满时,水位开始上升,由于水池的此部分空间比⑴段大,因此水池中水面上升的速度要比⑴段速度慢,则其图象是一段比⑴段中上升线段较缓的上升线段,由此可知答案应选B.
【变式题组】
01.如图所示,向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度h与注水时间t的函数关系式,大致是下列图象中的( )
02.某蓄水池的横截面示意图如图所示,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出,下面的图象能大致表示水的深度h和放水时间t之间的关系的是( )
03.用均匀的速度向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图表示(图中OAB为一折线),这个容器的形状是图中的( )
【例5】 已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边线运动,运动路径为:G→C→D→E→F→H相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象,如图2,若AB=6cm,则下列四个结论中正确的个数有( )
图1中的BC边长是8cm
图2中的M点表示第4秒时y的值为24cm2
图中的CD长是4cm
图2中的N点表示第12秒时y的值为18cm2
A. 1个 B. 2个 C. 3个 D. 4个
【解法指导】 若把点P由G→C→D→E→F→H对应的图象分别记为第I段、第II段、第III段、第IV段、第V段,则从图1和图2的对应情况可知:
由I的两端点横坐标,知由G到C运动2秒,可得GC=4cm,即BC=8cm;
∴a正确
M点的纵坐标等于S△ABD=;∴b正确
∵P在CD上的时间从图2知为2秒,∴CD==24cm
ABCDEFGH的周长为(AB+BC+DE)2=40cm
∴ AH=
∴ y= ∴d正确 故选D.
【变式题组】
01.(莆田)如图1,在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到的位置是( )
A. N处 B. P处 C. Q处 D.M处
02.(重庆綦江)如图1,在直角梯形ABCD中,动点P从点B出发,沿BC、CD运动至点D停止,设点P运动的路径为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
A. 3 B. 4 C. 5
演练巩固·反馈提高
01.(益阳)某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,图中描述了他上学的情景,下列说法错误的是( )
A. 修车时间为15分钟 B. 学校离家的距离为2000米
C. 到达学校时共用时间20分钟 D.自行车发生故障时离家距离为1000米
02.(宜昌)由于干旱,某水库的蓄水量随时间的增加而直线下降,若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( )
A. 干旱开始时,蓄水量每天减少20万米3
B.干旱开始后,蓄水量每天增加20万米3
C.干旱开始时,蓄水量为200万米3
D.干旱第50天时,蓄水量为1200万米3
03.(黑龙江大兴安岭)一个水池接有甲、乙、丙三个水管,先打开甲,一段时间后再打开乙,水池注满水后关闭甲,现时打开丙,直到水池中的水排空,水池中的水量V(m3)与时间t(h)之间的函数关系如图,则关于三个水管每小时的水流量,下列判断正确的是
A. 乙>甲 B. 丙>甲 C.甲>乙 D.丙>乙
04.(杭州)已知点P(x,y)在函数的图象上,那么点P应在平面直角坐标系中的( )
A. 第一象限 B.第二象限 C. 第三象限 D.第四象限
05.(大连)函数的自变量x的取值范围是( )
A.x≥-2 B. x>-2且x≠2 C.x≥0且x≠2 D.x≥-2且x≠2
06.已知某一函数的图象如图所示,根据图象回答下列问题.
⑴确定自变量的取值范围;
⑵求当x=-4,-2时y的值是多少?
⑶求当y=0,4时,x的值是多少?
⑷当x取何值时y的值最大?当x何值时y的值最小?
(5)当x在什么范围内取值时y随x的增大而增大?当x在什么范围内取值时y随x的增大而减小?
07.甲、乙两人在一次赛跑中,路程s与时间t的关系式如图所示,那么你可知道:
⑴这是一次_________米的赛跑;
⑵甲、乙两人中先跑到终点的是_______
(3) 乙在这次赛跑中的速度为______米/秒
第8讲 一次函数的图象与性质
考点·方法·破译
1.一次函数及图象:
⑴形如y=kx+b(k,b为常数,且k≠0),则y叫做x的一次函数,当b=0,k≠0时,y叫做x的正比例函数.
⑵正比例函数y=kx(k≠0)的图象是经过(0,0),(1,k)两点的直线,一次函数y=kx+b(k≠0)是经过(0,b)、(-,0)两点的直线.
2.一次函数的性质:
当k>0时,y随自变量x的增大而增大;当k<0时,y随x的增大而减小.
3.函数y=kx+b中的系数符号,决定图象的大致位置的增减性.
经典·考题·赏析
【例1】(山东)函数y=ax+b①和y=bx+a②(ab≠0)在同一坐标系中的图象可能是( )
【解法指导】A中①a>0,b>0,②b<0,a<0矛盾.B中①a<0,b<0,矛盾.C中①a>0,b>0②b>0,a=0矛盾.D中①a>0,b<0②b<0,a>0,故选D.
【变式题组】
01.(河北)如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
02.(安徽)已知函数y=kx+b的图象如左图,则y=2kx+b的图象可能是( )
03.下列图象中,表示一次函数y=mx+n与正比例函数y=mnx(m、n为常数,则mn≠0)的图象是( )
【例2】(绍兴)如图,一次函数y=x+5的图象经过点P(a,b)和Q(c,d)则a(c-d)-b(c-d)的值为_______.
【解法指导】因为点P(a,b),Q(c,d)在一次函数图象上,∴b=a+5,d=c+5∴a-b=-5,c-d=-5,a(c-d)-b(c-d)=(c-d)(a-b)=(-5)×(-5)=25
【变式题组】
01.如图一条直线l经过不同三点A(a,b),B(b,a)C(a-b,b-a)则直线l经过( )
A.第二、四象限 B.第一、三象限 C.第二、三、四象限 D.第一、三、四象限
02.(南京市八年级竞赛试题)已知三点A(2,3),B(5,4)C(-4,1)依次连接这三点,则( )
A.构成等边三角形B.构成直角三角形C.构成锐角三角形D.三点在同一条直线上
03.(四川省初二数学联赛试题)已知一次函数y=ax+b的图象经过点(0,1),它与坐标轴围成的图是等腰直角三角形,则a的值为_______.
【例3】如图,已知正方形ABCD的顶点坐标为A(1,1)、B(3,1)、C(3,3)、D(1,3),直线y=2x+b交AB于点E,交CD于点F.直线与y轴的交点为(0,b),则b的变化范围是_____.
【解法指导】直线y=2x+b是平行于直线y=2x的直线,当直线经过B点时,b最小,当x=3时,y=1
∴1=2×3+b, b=-5
当直线经过D点时,b最大,
所以当x=1时,y=3
∴3=2×1+b, b=1
∴-5≤b≤1
【变式题组】
01.线段y=-x+a(1≤b≤3),当a的值由-1增加到2时,该线段运动所经过的平面区域的面积为( )
A.6 B.8 C.9 D.10
02.(新知杯上海)在平面直角坐标系中有两点P(-1,1),Q(2,2),函数y=kx-1的图象与线段PQ延长线相交(交点不包括Q),则实数k的取值范围是_________.
03.(济南)阅读下面的材料:在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1= k2,且b1=b2,我们就称直线l1与直线l2平行.解答下面的问题:
⑴求过点P(1,4)且与已知直线y=-2x-1平行的直线l的函数表达式,并画出直线l的图象;
⑵设直线l分别与y轴、x轴交于点A、B,如果直线m:y=kx+t(t>0)与直线平行且交于x轴于点C,求出△ABC的面积S关于t的函数关系式.
【例4】已知一次函数y=kx+b,当自变量取值范围是2≤x≤6时,函数值的取值范围5≤y≤9.求此函数的解析式.
【解法指导】⑴当k>0,y随x的增大而增大,∴y=kx+b经过(2,5),(6,9)两点
∴∴,∴y=x+3
⑵当k<0,y随x的增大而减小,∴y=kx+b经过(2,9),(6,5)两点
∴∴,∴y=-x+11
∴所求解析式为y=x+3或y=-x+11
【变式题组】
01.已知一次函数y=kx+b,当-3≤x≤1时,对应y的值为1≤y≤9,则kb的值为( )
A.4 B. -6 C.-4或21 D.-6或14
02.(遂宁)已知整数x满足-5≤x≤5,y1=x+1,y2=2x+4,对任意一个x,m都取y1,、y2中的最小值,则m的最大值是( )
A.1 B. 2 C.24 D.-9
【例5】如图,直线y=-5x-5与x轴交于A,与y轴交于B,直线y=kx+b与x轴交于 C,与y轴交于B点,CD⊥AB交y轴于E.若CE=AB,求直线BC 的解析式.
【解法指导】由CE=AB,CD⊥AB可得△AOB≌△EOC,因而OB=OC而y=-5x-5与y轴交于B
∴B(0,-5)
∴C(5,0),而直线BC经过(0,-5),(5,0)可求得解析式y=x-5
【变式题组】
01.如图,在平面直角坐标系中,点P(x,y)是直线y=-x+6第一象限上的点,点A(5,0),O是坐标原点,△PAO的面积S.
⑴求S与x的函数关系式,并写出x的取值范围;
⑵探究:当P点运动到什么位置时△PAO的面积为10.
02.如图,直线l:y=-x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
⑴求A、B两点的坐标;
⑵求△COM的面积S与M的移动时间t之间的函数关系式;
⑶当t为何值时,△COM≌△AOB,并求此时M点的坐标.
03.如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过A(0,2)、B(4,2)两点.
⑴求直线AB的解析式;
⑵点C的坐标为(0,1),过点C作CD⊥AO交AB于D. x轴上的点P和A、B、C、D、O中的两个点所构成的三角形与△ACD全等,这样的三角形有_____个,请子啊图中画出其中两个三角形的示意图.
【例6】如图,已知直线y=-x+2与x轴、y轴分别交于点A和点B.另一条直线y=kx+b(k≠0)经过(1,0),且把△AOB分成两部分.⑴若△AOB被分成的两部分面积相等,求k和b的值;⑵若△AOB被分成的两部分的面积比为1:5,求k和b的值.
【解法指导】欲求k和b的值,需知道直线y=kx+b(k≠0)经过两已知点,而点C(1,0)在直线上,因而只需求出另一点的坐标即可.
解:⑴由题意得(2,0)、B(0,2),∴C为OA的中点,因而直线y=kx+b过OA中点且平分△AOB的面积时只可能韦中线BC.
∴y=kx+b经过C(1,0),(0,2)
∴∴k=2 b=2
⑵①设y=kx+b与OB交于M(0,t)则有S△OMC=S△CAN,∴MN∥x轴,∴N(,)
∴直线y=kx+b经过,),(1,0)∴ ∴
【变式题组】
01.如图,在平面直角坐标系xOy,已知直线AC的解析式为y=-x+2,直线AC交x轴于点C,交于y轴于点A.
⑴若一个等腰直角三角形OBD的顶点D与点C重合,直角顶点B在第一象限内,请直接写出点B的坐标;
⑵过点B作x轴的垂线l,在l上是否存一点P,使得△AOP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
⑶试在直线AC上求出到两坐标轴距离相等的所有点的坐标.
02.(浙江杭州)已知,直线y=-与x轴、y轴分别交于点A、B,以线段AB为直角边的第一象限内作等腰Rt△ABC,°,且点P(1,a)为坐标系中的一个动点.
⑴求三角形ABC的面积S△ABC;
⑵证明不论a取任何实数,三角形BOP的面积是一个常数;
⑶要使得△ABC和△ABP的面积相等,求实数a的值.
演练巩固·反馈提高
01.(芜湖)关于x的一次函数y=kx+k2+1的图象可能正确的是( )
02.一次函数y=kx-b和正比例函数y=kbx在同一直角坐标系内的大致图象不可能的是()
03.一次函数y=(m-1)x+m2+2的图象与y轴的交点的纵坐标是3,则m的值是()
A. B. C.-1 D.-2
04.直线y1=kx+b过第一、二、四象限,则直线y2=bx-k不经过()
A. 第一象限 B.第二象限 C.第三象限 D.第四象限
05.已知一次函数y=(1-2m)x+m-2,函数y随着x的增大而减小,且其图象不经过第一象限,则m的取值范围是( )
A.m> B.m≤2 C.<m<2 D. <m≤2
06.如图,点A、B、C、D在一次函数y=-2x+m的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A. 1 B.3 C.3(m-1) D. (m-2)
07.(绍兴)如图,在x轴上有五个点,它们横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0,则图中阴影部分的面积是( )
A. 12.5 B.25 C.12.5a D. 25a
08.(重庆)如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致是( )
09.(日照)如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A.(0,0) B.(,-) C.(-,-) D.(-,-)
10.(义务)李老师给出了一个函数,甲、乙、丙三位同学分别指出这个函数的一个特征.甲:它的图象经过第一象限;乙:它的图象经过第二象限;丙:在第一象限内函数值y随x增大而增大.在你学习的函数中,写出一个满足上述特征的函数解析式_________.
11.观察下列各直角坐标系中的直线AB,点P(x,y)是线段AB上的点,且x、y都是整数,请根据图中所包含的规律,回答下列问题:
⑴第5个图中满足条件的点P个数是_______;
⑵第n个图中满足条件的点P个数m与n之间的关系是________.
12.(十堰)直线y=kx+b经过点A(-2,0)和y轴上的一点B,如果△ABO(O为坐标原点)的面积为2,则b的值为________.
13.如图,长方形OABC的顶点B的坐标为(6,4),直线y=-x+b恰好平分长方形的面积,则b=_______.
14.如图,点B、C分别在两条直线y=2x和y=kx上,点A、D是x轴上两点,已知四边形ABCD是正方形,则k=______.
15.(东营)正方形A1B1C1O1,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2)则Bn的坐标是________.
16.点P为直线y=-3x+6上的一点,且点P到两坐标轴距离相等,则P点坐标为_____.
17.已知直线y1=x,y2=x+1,y3=-x+5的图象如图所示,若无论x取何值,y总取y1、y2、y3中最小的值,则y的最大值为_______.
18.已知一次函数y=kx+b的图象经过点P(0,-3),且与函数y=x+1的图象相交于点A().
⑴求a的值;
⑵若函数y=kx+b的图象与x轴的交点是B,函数y=x+1的图象与y轴的交点是C,求四边形ABOC的面积(其中O为坐标原点).
19.定义为一次函数y=px+q的特征数.
⑴求一次函数y=-2(x-1)的特征数;
⑵若特征数是的一次函数为正比例函数,求k的值.
20.已知:三点A(a,1)、B(3,1)、C(6,0),点A在正比例函数y=x的图象上.
⑴求a的值;
⑵点P为x轴上一动点,当△OAP与△CBP周长的和取得最小值时,求点P的坐标;
21.已知直线ln:y=-x+(n是正整数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1.设△A1OB1(O是平面直角坐标系的原点)的面积为s1.当n=2时,直线l2:y=-与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,?…,依次类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
?⑴求△A1OB1的面积s1;
⑵求s1+s2+s3+…+s2010的值.
22.(长沙)在平面直角坐标系中,一动点P(x,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动.图②是P点运动的路程s(个单位)与运动时间t(秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
⑴s与t之间的函数关系式是:_________;
(2)与图③相对应的P点的运动路径是:________;P点出发 _______秒首次到达点B;
⑶写出当3≤s≤8时,y与s之间的函数关系式,并在图③中补全函数图象.
培优升级·奥赛检测
01.已知abc≠0,且=t,则直线y=tx+t一定通过( )
A.第一、二象限 B.第二、三象限 C.第三、四象限 D.第一、四象限
02.一个一次函数的图象与直线y=+平行,与x轴、y轴的交点分别为A、B,并且过点(-1,-25),则在线段AB上(包括端点A、B)横坐标、纵坐标都是整数的点有( )
A.4个 B.5个 C.6个 D.7个
03.在一次函数y=-x+3的图象上取点P,作PA⊥x轴,PB⊥y轴,垂足分别为A、B,长方形OAPB的面积为2,则这样的点P共有( )
A.4个 B.3个 C.2个 D.1个
04.在直角坐标系中,x轴上的动点M(x,0)到定点P(5,5),Q(2,1)的距离分别为MP和MQ,若MP+MQ取最小值,则点M的坐标为________.
05.已知点A(0,2)、B(4,0),点C、D分别在直线x=1与x=2上运动,且CD∥x轴,当AC+CD+DB的值最小值,点C的坐标为_____________.
06.在直角坐标系中,有两个点A(-8,3)、B(-4,5)以及动点C(0,n)、D(m,0).当四边形ABCD的周长最短时,的值为_________.
07.已知函数y=(a-2)x-3a-1,当自变量x的值范围为3≤x≤5时,y既能取到大于5的值,又能取到小于3的值,求实数a的取值范围.
08.(荆州市八年级数学联赛试题)已知一次函数y=ax+b(a为整数)的图象过(98,19),它与x轴的交点为(p,0),与y轴的交点为(0,q),若P为质数,q是正整数,问符合条件的一次函数是否存在?若存在,求出解析式;若存在,说明理由.
09.若直线y=mx-3,y=-1,y=3和x=1所围成的四边形面积为12,求m.
10.设f(x)=kx+1是x的函数,若m(k)表示函数f(x)=kx+1在1≤x≤3条件下的最大值,求函数m(k)的解析式,并作出图象.
第9讲 一次函数与方程、不等式
考点·方法·破译
1. 一次函数与一元一次方程的关系:任何一元一次方程都可以转化成kx+b=0(k、b为常数,k≠0)的形式,可见一元一次方程是一次函数的一个特例.即在y=kx+b中,当y=0时则为一元一次方程.
2. 一次函数与二元一次方程(组)的关系:
⑴任何二元一次方程ax+by=c(a、b、c为常数,且a≠0,b≠0)都可以化为y=的形式,因而每个二元一次方程都对应一个一次函数;
⑵从“数”的角度看,解方程组相当于求两个函数的函数值相等时自变量的取值,以及这个函数值是什么;从“形”的角度看,解方程组相当于确定两个函数图像交点的坐标.
3. 一次函数与一元一次不等式的关系:由于任何一元一次不等式都可以转化成ax+b>0或ax+b<0(a、b为常数,a≠0)的形式,所以解一元一次不等式可以看成是当一次函数的函数值大于或小于0时,求相应自变量的取值范围.
经典·考题·赏析
【例1】直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
A.x>-1 B.x<-1 C.x<-2 D.无法确定
【解法指导】由图象可知l1与l2的交点坐标为(-1,-2),即当x=-1时,两函数的函数值相等;当x>-1时,l2的位置比l1高,因而k2x>k1x+b;当当x<-1时,l1的位置比l2高,因而k2x<k1x+b.因此选A.
【变式题组】
01.(咸宁)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为________.
第1题图 第2题图 第3题图 第4题图
02.(浙江金华)一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
A.0 B.1 C.2 D.3
03. 如图,已知一次函数y=2x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式2x+b>ax-3的解集是________.
04. (武汉)如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式x>kx+b>-2的解集为_________.
【例2】若直线l1:y=x-2与直线l2:y=3-mx在同一平面直角坐标系的交点在第一象限,求m的取值范围.
【解法指导】直线交点坐标在第一象限,即对应方程组的解满足,从而求出m的取值范围.
解:,∴,∵,∴,即,∴-1<m<.
【变式题组】
01. 如果直线y=kx+3与y=3x-2b的交点在x轴上,当k=2时,b等于( )
A.9 B.-3 C. D.
02. 若直线与直线相较于x轴上一点,则直线不经过( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
03. 两条直线y1=ax+b,y2=cx+5,学生甲解出它们的交点坐标为(3,-2),学生乙因抄错了c而解出它们的交点坐标为(,),则这两条直线的解析式为____________.
04. 已知直线y=3x和y=2x+k的交点在第三象限,则k的取值范围是________.
【例3】(四川省初二数学联赛试题)在直角坐标系中,若一点的纵横坐标都是整数,则称该点为整点,设k为整数,当直线y=x-2与y=kx+k的交点为整点时,k的取值可以取( )
A.4个 B.5个 C.6个 D.7个
【解法指导】两直线的交点为整点即对应方程组的解均为整数.
解:由得,
∵两直线交点为整数,
∴x、y均为整数,
又当x为整数时,y为整数,
∴为整数即可,,
∵k-1是整数,
∴k-1=±1,±3时,x、y为整数,
∴k=-2,0,2,4.
所以选A.
【变式题组】
01. (广西南宁)从2,3,4,5这四个数中,任取两个数p和q(p≠q),构成函数y=px-2和y=x+q,并使这两个函数图象的交点在直线x=2的右侧,则这样的有序数对(p,q)共有( )
A.12对 B.6对 C.5对 D.3对
02. (浙江竞赛试题)直线l:y=px(p是不等于0的整数)
