华东师大版九年级数学下册 26.1 二次函数 同步测试题(Word版 有答案)
文档属性
| 名称 | 华东师大版九年级数学下册 26.1 二次函数 同步测试题(Word版 有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 47.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览




文档简介
26.1
二次函数
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
1.
若是二次函数,则等于(
)
A.
B.
C.
D.不能确定
?
2.
下列函数是二次函数的有(
)
;;;.
A.个
B.个
C.个
D.个
?
3.
若函数?是二次函数,则的值为(?
?
?
?
)
A.
B.
C.
D.
?
4.
九年级举行篮球赛,初赛采用单循环制(每两个班之间都进行一场比赛),据统计,比赛共进行了场,求九年级共有多少个班.若设九年级共有个班,根据题意列出的方程是(?
?
?
?
)
A.
B.
C.
D.
?
5.
下列是二次函数的是(
)
A.
B.
C.
D.
?
6.
我市共享单车为市民出行带来了方便,某共享单车公司第一个月投放辆共享单车,计划第三个月投放共享单车辆,设该公司第二个月和第三个月投放共享单车数量的月平均增长率为,那么与的函数关系式是(?
?
?
?
)
A.
B.
C.
D.
?
7.
某商店从厂家一每件元的价格购进一批商品,该商店可以自行定价.若每件商品售为元,则可卖出件商品,那商品所赚钱元与售价元的函数关系为(
)
A.
B.
C.
D.
?
8.
某产品进货单价为元,按一件售出时,能售件,如果这种商品每涨价元,其销售量就减少件,设每件产品涨元,所获利润为元,可得函数关系式为(
)
A.
B.
C.
D.
?
9.
长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则与的关系式为(
)
A.
B.
C.
D.
?
10.
如图,四边形中,,,,设的长为,四边形的面积为,则与之间的函数关系式是(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
11.
正方体的表面积与正方体的棱长之间的函数关系式为________.
?
12.
当________时,是关于的二次函数.
?
13.
在半径为的圆中截取两个半径分别为和的圆,且,若所剩的阴影部分的面积为,则与的关系式为________,当________时,有最大值________.
?
14.
已知函数,当________时,它是二次函数.
?
15.
某工厂实行技术改造,产量年均增长率为,已知年产量为万件,那么年的产量与间的关系式为________(万件).
?
16.
已知长方形的周长为,其中一边长为,面积为,则这个长方形的面积与之间的关系可表示为________
?
17.
长方体底面周长为,高为,则长方体体积关于底面的一条边长的函数解析式是________,其中的取值范围是________.
?
18.
若二次函数,存在不同实数,且使得,则________.
?
19.
在边长为的正方形中间挖去一个长为的小正方形,剩下的四方框形的面积为,则与间的函数关系式为________.
?
20.
某地区原有个养殖场,平均每个养殖场养奶牛头,后来由于市场原因,决定减少养殖场的数量,当养殖场每减少个时,平均每个养殖场奶牛数将增加头,如果养殖场减少个,则求该地区奶牛总数(头)与(个)之间的函数表达式为________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,用长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积与它与墙平行的边的长之间的函数.
?
22.
一条隧道的横截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为米.如果隧道下部的宽度大于米但不超过米,求隧道横截面积(平方米)关于上部半圆半径(米)的函数解析式及函数的定义域.
?
23.
某商场将进货单价为元的裤子,按元/件出售时,每月能卖出件,已知该商场裤子每涨价元月销量减少件.若这种裤子售价为元/件,该裤子获得的利润为元,请写出与的函数关系式.
?
24.
某商场以每件元的价格购进一种商品,试销中发现,这种商品每天的销售量(件)与每件的销售价(元)满足一次函数关系.请写出商场卖这种商品每天的销售利润(元)与每件销售价(元)之间的函数关系式.
?
25.
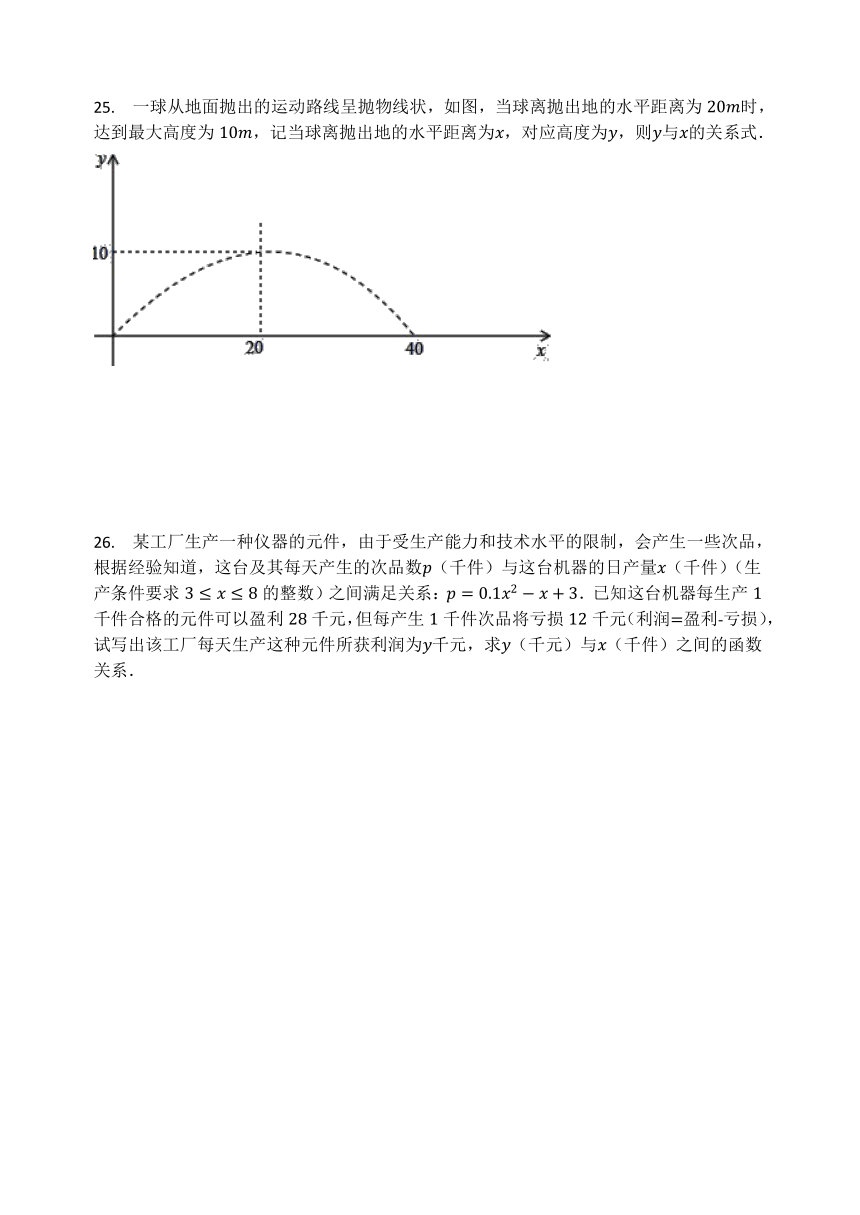
一球从地面抛出的运动路线呈抛物线状,如图,当球离抛出地的水平距离为时,达到最大高度为,记当球离抛出地的水平距离为,对应高度为,则与的关系式.
?
26.
某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,这台及其每天产生的次品数(千件)与这台机器的日产量(千件)(生产条件要求的整数)之间满足关系:.已知这台机器每生产千件合格的元件可以盈利千元,但每产生千件次品将亏损千元(利润盈利-亏损),试写出该工厂每天生产这种元件所获利润为千元,求(千元)与(千件)之间的函数关系.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
由题意,得
=,且,
解得=,
2.
【答案】
A
【解答】
解:符合二次函数的定义,故正确;
是反比例函数,故错误;
是正比例函数,故错误;
当时,不是二次函数,故错误;
是一次函数,故错误;
.是一次函数,故错误.
综上所述,二次函数的个数是个.
故选:.
3.
【答案】
B
【解答】
解:由二次函数定义得:
且,
解得且,
故.
故选.
4.
【答案】
B
【解答】
解:设九年级共有个班,
则每个班都要比赛场,
且两班之间只有一场比赛,
则可设方程为.
故选.
5.
【答案】
A
【解答】
解:、,故本选项正确;
、,不是整式,故本选项错误;
、整理后含三次项,故本选项错误;
、不含二次项,故本选项错误.
故选.
6.
【答案】
C
【解答】
解:设该公司第二、三两个月投放单车数量的月平均增长率为,
依题意得第三个月第三个月投放单车辆,
则.
故选.
7.
【答案】
B
【解答】
解:每件的利润为,
∴
.
故选.
8.
【答案】
D
【解答】
解:由题意,得
,
.
故选.
9.
【答案】
C
【解答】
解:设小正方形边长为,由题意知:
现在底面长为,宽为,
故,
故选.
10.
【答案】
C
【解答】
解:作,,两线交于点,作垂足为点,
∵
,即
∴
又∵
,
∴
∴
,,
设,则,,
,
在中,由勾股定理得,
,即,
解得:,
∴
.
故选:.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:根据题意可得:.
故答案为:.
12.
【答案】
【解答】
解:∵
是关于的二次函数,
∴
,,
,
故答案为:.
13.
【答案】
,,
【解答】
解:∵
半径为的圆中截取两个半径分别为和的圆,且,
∴
,
∵
所剩的阴影部分的面积为,
则与的关系式为:,
当时,最大为:.
故答案为:,.
14.
【答案】
【解答】
解:∵
函数是二次函数,
∴
且.
解得.
故答案是:.
15.
【答案】
【解答】
解:∵
某工厂实行技术改造,产量年均增长率为,年产量为万件,
∴
年产量为:;
年的产量与间的关系式为:;
即:.
故答案为:.
16.
【答案】
【解答】
解::矩形周长为
…两邻边之和为
________….若一边长为,则另一边长为;面积为
∴
即
故答案是:
17.
【答案】
,
【解答】
解:∵
长方体底面周长为,底面的一条边长,
∴
底面的另一条边长为:,根据题意得出:
.
故答案为:,.
18.
【答案】
【解答】
解:由,
得,
即,
∵
,
∴
,
故.
19.
【答案】
【解答】
解:∵
剩下的四方框形的面积边长为的正方形面积-长为的小正方形面积,
∴
.
故填空答案:.
20.
【答案】
【解答】
解:∵
当养殖场每减少个时,平均每个养殖场奶牛数将增加头,
∴
当养殖场减少个,则该地区奶牛总数(头)与(个)之间的函数表达式为:
.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:∵
与墙平行的边的长为,则垂直于墙的边长为:,
根据题意得出:.
【解答】
解:∵
与墙平行的边的长为,则垂直于墙的边长为:,
根据题意得出:.
22.
【答案】
解:半圆的半径为,矩形的另一边长为,
则:隧道截面的面积,
即;
∵
,
∴
.
【解答】
解:半圆的半径为,矩形的另一边长为,
则:隧道截面的面积,
即;
∵
,
∴
.
23.
【答案】
解:根据题意可得:
.
【解答】
解:根据题意可得:
.
24.
【答案】
解:由题意,得每件商品的销售利润为元,那么件的销售利润为.
又∵
,
∴
,
即.
∵
,
∴
.
又∴
,
∴
,即.
∴
.
∴
所求关系式为.
【解答】
解:由题意,得每件商品的销售利润为元,那么件的销售利润为.
又∵
,
∴
,
即.
∵
,
∴
.
又∴
,
∴
,即.
∴
.
∴
所求关系式为.
25.
【答案】
解:由题意可得出:抛物线过点,
故设解析式为:,
将代入得出:,
解得:,
则关于的函数解析式为:.
【解答】
解:由题意可得出:抛物线过点,
故设解析式为:,
将代入得出:,
解得:,
则关于的函数解析式为:.
26.
【答案】
解:根据题意可得:
(的整数).
【解答】
解:根据题意可得:
(的整数).
二次函数
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
1.
若是二次函数,则等于(
)
A.
B.
C.
D.不能确定
?
2.
下列函数是二次函数的有(
)
;;;.
A.个
B.个
C.个
D.个
?
3.
若函数?是二次函数,则的值为(?
?
?
?
)
A.
B.
C.
D.
?
4.
九年级举行篮球赛,初赛采用单循环制(每两个班之间都进行一场比赛),据统计,比赛共进行了场,求九年级共有多少个班.若设九年级共有个班,根据题意列出的方程是(?
?
?
?
)
A.
B.
C.
D.
?
5.
下列是二次函数的是(
)
A.
B.
C.
D.
?
6.
我市共享单车为市民出行带来了方便,某共享单车公司第一个月投放辆共享单车,计划第三个月投放共享单车辆,设该公司第二个月和第三个月投放共享单车数量的月平均增长率为,那么与的函数关系式是(?
?
?
?
)
A.
B.
C.
D.
?
7.
某商店从厂家一每件元的价格购进一批商品,该商店可以自行定价.若每件商品售为元,则可卖出件商品,那商品所赚钱元与售价元的函数关系为(
)
A.
B.
C.
D.
?
8.
某产品进货单价为元,按一件售出时,能售件,如果这种商品每涨价元,其销售量就减少件,设每件产品涨元,所获利润为元,可得函数关系式为(
)
A.
B.
C.
D.
?
9.
长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则与的关系式为(
)
A.
B.
C.
D.
?
10.
如图,四边形中,,,,设的长为,四边形的面积为,则与之间的函数关系式是(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
11.
正方体的表面积与正方体的棱长之间的函数关系式为________.
?
12.
当________时,是关于的二次函数.
?
13.
在半径为的圆中截取两个半径分别为和的圆,且,若所剩的阴影部分的面积为,则与的关系式为________,当________时,有最大值________.
?
14.
已知函数,当________时,它是二次函数.
?
15.
某工厂实行技术改造,产量年均增长率为,已知年产量为万件,那么年的产量与间的关系式为________(万件).
?
16.
已知长方形的周长为,其中一边长为,面积为,则这个长方形的面积与之间的关系可表示为________
?
17.
长方体底面周长为,高为,则长方体体积关于底面的一条边长的函数解析式是________,其中的取值范围是________.
?
18.
若二次函数,存在不同实数,且使得,则________.
?
19.
在边长为的正方形中间挖去一个长为的小正方形,剩下的四方框形的面积为,则与间的函数关系式为________.
?
20.
某地区原有个养殖场,平均每个养殖场养奶牛头,后来由于市场原因,决定减少养殖场的数量,当养殖场每减少个时,平均每个养殖场奶牛数将增加头,如果养殖场减少个,则求该地区奶牛总数(头)与(个)之间的函数表达式为________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
如图,用长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积与它与墙平行的边的长之间的函数.
?
22.
一条隧道的横截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为米.如果隧道下部的宽度大于米但不超过米,求隧道横截面积(平方米)关于上部半圆半径(米)的函数解析式及函数的定义域.
?
23.
某商场将进货单价为元的裤子,按元/件出售时,每月能卖出件,已知该商场裤子每涨价元月销量减少件.若这种裤子售价为元/件,该裤子获得的利润为元,请写出与的函数关系式.
?
24.
某商场以每件元的价格购进一种商品,试销中发现,这种商品每天的销售量(件)与每件的销售价(元)满足一次函数关系.请写出商场卖这种商品每天的销售利润(元)与每件销售价(元)之间的函数关系式.
?
25.
一球从地面抛出的运动路线呈抛物线状,如图,当球离抛出地的水平距离为时,达到最大高度为,记当球离抛出地的水平距离为,对应高度为,则与的关系式.
?
26.
某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,这台及其每天产生的次品数(千件)与这台机器的日产量(千件)(生产条件要求的整数)之间满足关系:.已知这台机器每生产千件合格的元件可以盈利千元,但每产生千件次品将亏损千元(利润盈利-亏损),试写出该工厂每天生产这种元件所获利润为千元,求(千元)与(千件)之间的函数关系.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
由题意,得
=,且,
解得=,
2.
【答案】
A
【解答】
解:符合二次函数的定义,故正确;
是反比例函数,故错误;
是正比例函数,故错误;
当时,不是二次函数,故错误;
是一次函数,故错误;
.是一次函数,故错误.
综上所述,二次函数的个数是个.
故选:.
3.
【答案】
B
【解答】
解:由二次函数定义得:
且,
解得且,
故.
故选.
4.
【答案】
B
【解答】
解:设九年级共有个班,
则每个班都要比赛场,
且两班之间只有一场比赛,
则可设方程为.
故选.
5.
【答案】
A
【解答】
解:、,故本选项正确;
、,不是整式,故本选项错误;
、整理后含三次项,故本选项错误;
、不含二次项,故本选项错误.
故选.
6.
【答案】
C
【解答】
解:设该公司第二、三两个月投放单车数量的月平均增长率为,
依题意得第三个月第三个月投放单车辆,
则.
故选.
7.
【答案】
B
【解答】
解:每件的利润为,
∴
.
故选.
8.
【答案】
D
【解答】
解:由题意,得
,
.
故选.
9.
【答案】
C
【解答】
解:设小正方形边长为,由题意知:
现在底面长为,宽为,
故,
故选.
10.
【答案】
C
【解答】
解:作,,两线交于点,作垂足为点,
∵
,即
∴
又∵
,
∴
∴
,,
设,则,,
,
在中,由勾股定理得,
,即,
解得:,
∴
.
故选:.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:根据题意可得:.
故答案为:.
12.
【答案】
【解答】
解:∵
是关于的二次函数,
∴
,,
,
故答案为:.
13.
【答案】
,,
【解答】
解:∵
半径为的圆中截取两个半径分别为和的圆,且,
∴
,
∵
所剩的阴影部分的面积为,
则与的关系式为:,
当时,最大为:.
故答案为:,.
14.
【答案】
【解答】
解:∵
函数是二次函数,
∴
且.
解得.
故答案是:.
15.
【答案】
【解答】
解:∵
某工厂实行技术改造,产量年均增长率为,年产量为万件,
∴
年产量为:;
年的产量与间的关系式为:;
即:.
故答案为:.
16.
【答案】
【解答】
解::矩形周长为
…两邻边之和为
________….若一边长为,则另一边长为;面积为
∴
即
故答案是:
17.
【答案】
,
【解答】
解:∵
长方体底面周长为,底面的一条边长,
∴
底面的另一条边长为:,根据题意得出:
.
故答案为:,.
18.
【答案】
【解答】
解:由,
得,
即,
∵
,
∴
,
故.
19.
【答案】
【解答】
解:∵
剩下的四方框形的面积边长为的正方形面积-长为的小正方形面积,
∴
.
故填空答案:.
20.
【答案】
【解答】
解:∵
当养殖场每减少个时,平均每个养殖场奶牛数将增加头,
∴
当养殖场减少个,则该地区奶牛总数(头)与(个)之间的函数表达式为:
.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:∵
与墙平行的边的长为,则垂直于墙的边长为:,
根据题意得出:.
【解答】
解:∵
与墙平行的边的长为,则垂直于墙的边长为:,
根据题意得出:.
22.
【答案】
解:半圆的半径为,矩形的另一边长为,
则:隧道截面的面积,
即;
∵
,
∴
.
【解答】
解:半圆的半径为,矩形的另一边长为,
则:隧道截面的面积,
即;
∵
,
∴
.
23.
【答案】
解:根据题意可得:
.
【解答】
解:根据题意可得:
.
24.
【答案】
解:由题意,得每件商品的销售利润为元,那么件的销售利润为.
又∵
,
∴
,
即.
∵
,
∴
.
又∴
,
∴
,即.
∴
.
∴
所求关系式为.
【解答】
解:由题意,得每件商品的销售利润为元,那么件的销售利润为.
又∵
,
∴
,
即.
∵
,
∴
.
又∴
,
∴
,即.
∴
.
∴
所求关系式为.
25.
【答案】
解:由题意可得出:抛物线过点,
故设解析式为:,
将代入得出:,
解得:,
则关于的函数解析式为:.
【解答】
解:由题意可得出:抛物线过点,
故设解析式为:,
将代入得出:,
解得:,
则关于的函数解析式为:.
26.
【答案】
解:根据题意可得:
(的整数).
【解答】
解:根据题意可得:
(的整数).
