苏科版九年级数学下册 7.6 用锐角三角函数解决问题 同步测试题(Word版 有答案)
文档属性
| 名称 | 苏科版九年级数学下册 7.6 用锐角三角函数解决问题 同步测试题(Word版 有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 251.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览

文档简介
7.6
用锐角三角函数解决问题
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
如图,上午时一条船从出发(海里/时)向正东航行,时分到处,经测小岛在北偏东,在北偏东方向,那么的距离为(
)
A.海里
B.海里
C.海里
D.海里
?
2.
如图,为测量一棵与地面垂直的树的高度,在距离树的底端米的处,测得树顶的仰角为,则树的高度为(
)
A.米
B.米
C.米
D.米
?
3.
如图,某一大坝的横断面是梯形,坝顶宽=米,斜坡=米,坝高米,斜坡的坡度=,则坝底宽是(
)米.
A.
B.
C.
D.
?
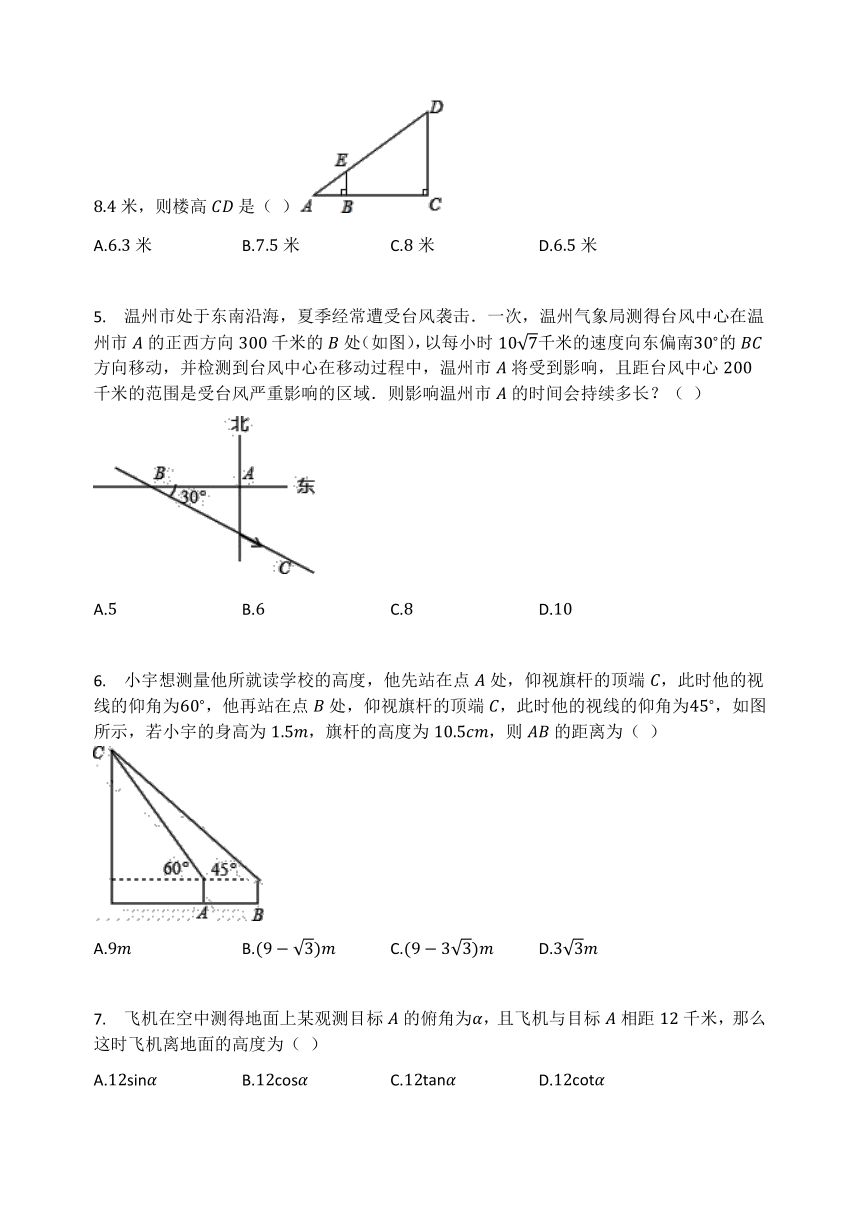
4.
如图,利用标杆测量建筑物的高度,如果标杆长为米,若,米,则楼高是(
)
A.米
B.米
C.米
D.米
?
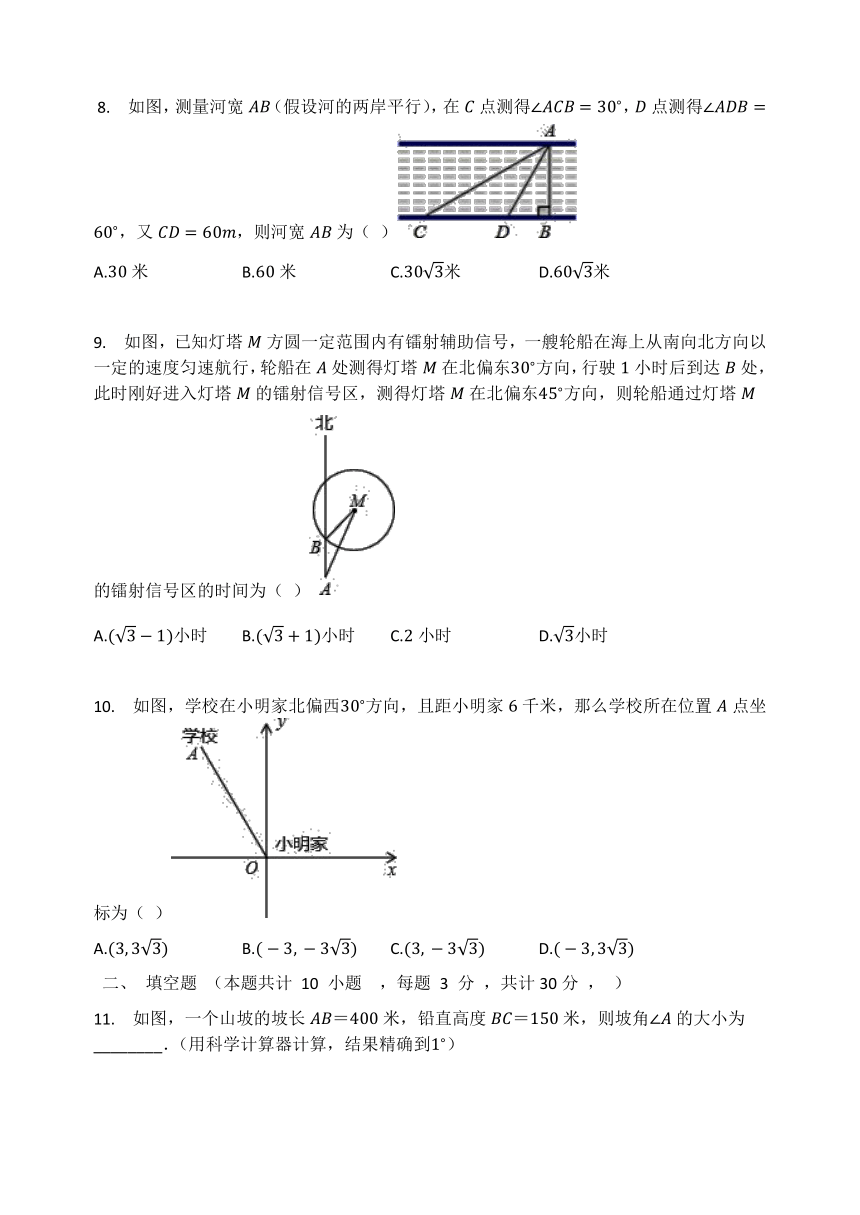
5.
温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市的正西方向千米的处(如图),以每小时千米的速度向东偏南的方向移动,并检测到台风中心在移动过程中,温州市将受到影响,且距台风中心千米的范围是受台风严重影响的区域.则影响温州市的时间会持续多长?(
)
A.
B.
C.
D.
?
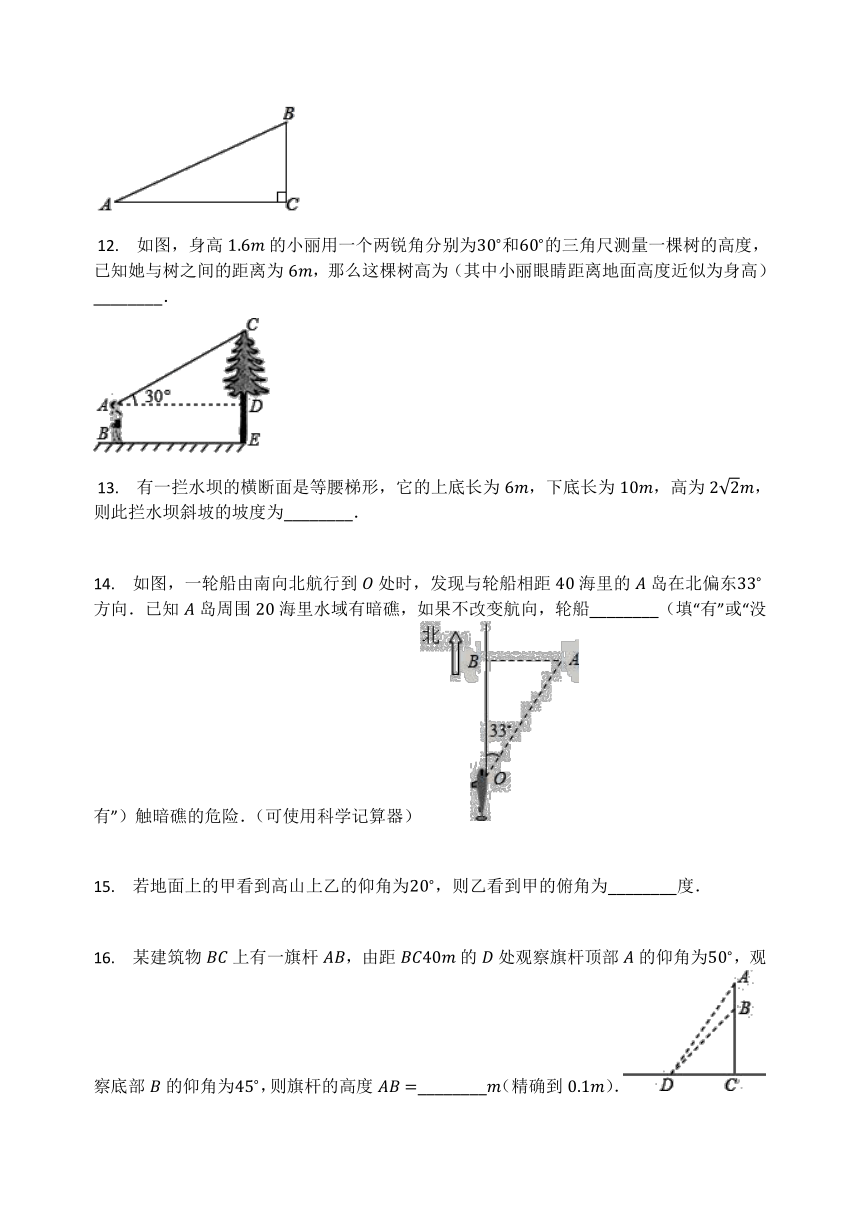
6.
小宇想测量他所就读学校的高度,他先站在点处,仰视旗杆的顶端,此时他的视线的仰角为,他再站在点处,仰视旗杆的顶端,此时他的视线的仰角为,如图所示,若小宇的身高为,旗杆的高度为,则的距离为(
)
A.
B.
C.
D.
?
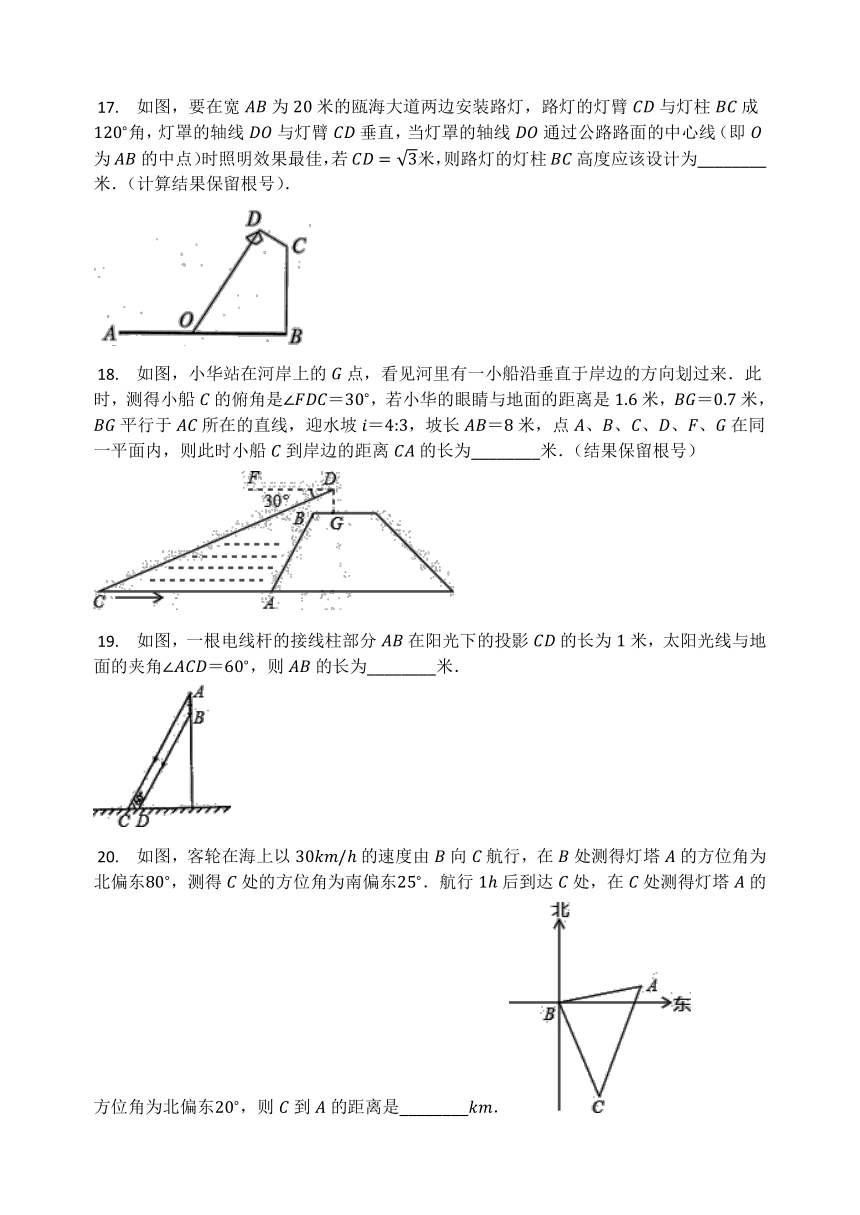
7.
飞机在空中测得地面上某观测目标的俯角为,且飞机与目标相距千米,那么这时飞机离地面的高度为(
)
A.
B.
C.
D.
?8.
如图,测量河宽(假设河的两岸平行),在点测得,点测得,又,则河宽为(
)
A.米
B.米
C.米
D.米
?
9.
如图,已知灯塔方圆一定范围内有镭射辅助信号,一艘轮船在海上从南向北方向以一定的速度匀速航行,轮船在处测得灯塔在北偏东方向,行驶小时后到达处,此时刚好进入灯塔的镭射信号区,测得灯塔在北偏东方向,则轮船通过灯塔的镭射信号区的时间为(
)
A.小时
B.小时
C.小时
D.小时
?
10.
如图,学校在小明家北偏西方向,且距小明家千米,那么学校所在位置点坐标为(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
如图,一个山坡的坡长=米,铅直高度=米,则坡角的大小为________.(用科学计算器计算,结果精确到)
?12.
如图,身高的小丽用一个两锐角分别为和的三角尺测量一棵树的高度,已知她与树之间的距离为,那么这棵树高为(其中小丽眼睛距离地面高度近似为身高)________.
?13.
有一拦水坝的横断面是等腰梯形,它的上底长为,下底长为,高为,则此拦水坝斜坡的坡度为________.
?
14.
如图,一轮船由南向北航行到处时,发现与轮船相距海里的岛在北偏东方向.已知岛周围海里水域有暗礁,如果不改变航向,轮船________(填“有”或“没有”)触暗礁的危险.(可使用科学记算器)
?
15.
若地面上的甲看到高山上乙的仰角为,则乙看到甲的俯角为________度.
?
16.
某建筑物上有一旗杆,由距的处观察旗杆顶部的仰角为,观察底部的仰角为,则旗杆的高度________(精确到).
?17.
如图,要在宽为米的瓯海大道两边安装路灯,路灯的灯臂与灯柱成角,灯罩的轴线与灯臂垂直,当灯罩的轴线通过公路路面的中心线(即为的中点)时照明效果最佳,若米,则路灯的灯柱高度应该设计为________米.(计算结果保留根号).
?18.
如图,小华站在河岸上的点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船的俯角是=,若小华的眼睛与地面的距离是米,=米,平行于所在的直线,迎水坡=,坡长=米,点、、、、、在同一平面内,则此时小船到岸边的距离的长为________米.(结果保留根号)
?19.
如图,一根电线杆的接线柱部分在阳光下的投影的长为米,太阳光线与地面的夹角=,则的长为________米.
?20.
如图,客轮在海上以的速度由向航行,在处测得灯塔的方位角为北偏东,测得处的方位角为南偏东.航行后到达处,在处测得灯塔的方位角为北偏东,则到的距离是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
已知电线杆直立于地面,它的影子恰好照在土坡的坡面和地面上.如果与地面成,,米,米,求电线杆的长.
?
22.
如图,甲楼的底端处与乙楼的底端处相距,从甲楼顶部处看乙楼顶部处的仰角的度数为.从甲楼顶部处看乙楼底部处的俯角的度数为.分别求甲楼和乙楼的高为多少(精确到).(参考数据:,,,,,)
?
23.
如图,海上有一灯塔,在它周围海里内有暗礁.一艘海轮以海里/时的速度由西向东方向航行,行至点处测得灯塔在它的北偏东的方向上,继续向东行驶分钟后,到达处又测得灯塔在它的北偏东方向上,如果海轮不改变方向继续前进有没有触礁的危险?
?
24.
如图,道路边有一棵树,身高米的某人站在水平地面的点处,从点测得树的顶端点的仰角为,树的底部点的俯角为,求树的高度.
?
25.
如图,小芳站在地面上处放风筝,风筝飞到处时的线长为米,这时测得,牵引底端与地面的距离为米,求此时风筝离地面的高度.(结果精确到米)(参考数据:,,)
?
26.
如图,小明设计了一个“简易量角器”:在中,,,,在边上有一系列点,,,使得,,,….
(1)连接,求的度数;
(2)求线段的长(结果精确到,参考数据:,,).
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:如图,过点作于点.
由题意得,(海里),.
在直角中,海里.
在直角中,,则,
所以(海里).
故选.
2.
【答案】
C
【解答】
在中,
∵
=米,为,
∴
==(米).
3.
【答案】
C
【解答】
过点作于点,过点作于点,则四边形是矩形
∴
==,==,
在中,,
∵
=,
∴
==,
即==米.
4.
【答案】
B
【解答】
解:如图,∵
在中,,米,,
∴
(米).
又∵
米,
∴
米.
又∵
在直角中,,,
∴
(米)
故选:.
5.
【答案】
D
【解答】
解:过点作于,
由题意得,,
则,
设台风中心距点处,刚好处在上的,两点则,
在中,,,
则,
从而可得:,
故镇受台风严重影响的时间为.
故选.
6.
【答案】
C
【解答】
解:如图,
,
在中,,
在中,,
.
故选:.
7.
【答案】
A
【解答】
解:如图:为飞机离地面的高度,
所以在直角三角形中,,,
则,
故选:.
8.
【答案】
C
【解答】
解:∵
,,
∴
,
∴
,
在中,
.
故选.
9.
【答案】
B
【解答】
解:连接,过点作于.
在中,∵
,
∴
,
在中,∵
,
∴
,
∴
,
∴
:.
故轮船通过灯塔的镭射信号区的时间为小时.
故选.
10.
【答案】
D
【解答】
解:∵
学校在小明家北偏西方向,且距小明家千米,
∴
,.
∵
,
∴
,.
即点坐标为.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
∵
=米,=米,
∴
.
∴
=.
12.
【答案】
【解答】
由题意得:=,
在中,
∴
=,又=
∴
===,
所以树的高度为.
13.
【答案】
【解答】
解:如图,作于,于,
,,.
∵
,,为等腰梯形.
∴
,.
∵
.
坡角.
14.
【答案】
没有
【解答】
解:已知,,
则.
所以轮船没有触暗礁的危险.
15.
【答案】
【解答】
解:若地面上的甲看到高山上乙的仰角为,则乙看到甲的俯角为.
故答案为:
16.
【答案】
【解答】
解:根据题意:在中,有.
在中,有.
∴
(米).
17.
【答案】
【解答】
解:如图,延长,交于点.
∵
,,米,米,
∴
在直角中,米,
(米),
∵
,,
∴
,
∴
,
∴
(米),
∴
(米).
故答案为:.
18.
【答案】
【解答】
过点作于点,延长交于点,得和矩形.
∵
,=米,
∴
,.
∵
=,=,
∴
==,
==.
在中,
∵
==,=,,
∴
=.
又∵
=,
即,
∴
=(米).
19.
【答案】
【解答】
作于,于.
∵
=,=,
∴
=.
在中=,,
∴
=(米).
20.
【答案】
【解答】
解:过点作于点.
在中,∵
,,,
∴
,
在中,∵
,,
∴
,
∴
.
即到的距离为.
故答案为.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:如图,延长交的延长线于点,作于.
∵
在中,,,,
∴
.
∵
在中,,,
∴
,
∴
.
∵
在中,,,
∴
.
故电线杆的长为米.
【解答】
解:如图,延长交的延长线于点,作于.
∵
在中,,,,
∴
.
∵
在中,,,
∴
,
∴
.
∵
在中,,,
∴
.
故电线杆的长为米.
22.
【答案】
甲楼的高约为,乙楼的高约为.
【解答】
解:由题意,得,,,,
在中,,
∴
,
在?中,,
∴
,
∴
.
23.
【答案】
解:过作.
海里.
∵
,
∴
∴
海里.
在直角中,海里.
∵
∴
海轮不改变方向继续前进没有触礁的危险.
【解答】
解:过作.
海里.
∵
,
∴
∴
海里.
在直角中,海里.
∵
∴
海轮不改变方向继续前进没有触礁的危险.
24.
【答案】
树的高度为.
【解答】
解:在中,
∵
,,
∴
,
在中,∵
,∴
,
25.
【答案】
此时风筝离地面的高度约为米.
【解答】
解:在中,(米),
米米米.
26.
【答案】
解:(1)如下图一所示:
∵
在边上有一系列点,,,使得,,,…,
∴
,
∵
,
∴
,
即的度数是;
(2)∵
在中,,,,,
∴
,
∴
,
∵
,,
∴
,
∵
,,
∴
,
即线段的长是.
【解答】
解:(1)如下图一所示:
∵
在边上有一系列点,,,使得,,,…,
∴
,
∵
,
∴
,
即的度数是;
(2)∵
在中,,,,,
∴
,
∴
,
∵
,,
∴
,
∵
,,
∴
,
即线段的长是.
用锐角三角函数解决问题
同步测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
如图,上午时一条船从出发(海里/时)向正东航行,时分到处,经测小岛在北偏东,在北偏东方向,那么的距离为(
)
A.海里
B.海里
C.海里
D.海里
?
2.
如图,为测量一棵与地面垂直的树的高度,在距离树的底端米的处,测得树顶的仰角为,则树的高度为(
)
A.米
B.米
C.米
D.米
?
3.
如图,某一大坝的横断面是梯形,坝顶宽=米,斜坡=米,坝高米,斜坡的坡度=,则坝底宽是(
)米.
A.
B.
C.
D.
?
4.
如图,利用标杆测量建筑物的高度,如果标杆长为米,若,米,则楼高是(
)
A.米
B.米
C.米
D.米
?
5.
温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市的正西方向千米的处(如图),以每小时千米的速度向东偏南的方向移动,并检测到台风中心在移动过程中,温州市将受到影响,且距台风中心千米的范围是受台风严重影响的区域.则影响温州市的时间会持续多长?(
)
A.
B.
C.
D.
?
6.
小宇想测量他所就读学校的高度,他先站在点处,仰视旗杆的顶端,此时他的视线的仰角为,他再站在点处,仰视旗杆的顶端,此时他的视线的仰角为,如图所示,若小宇的身高为,旗杆的高度为,则的距离为(
)
A.
B.
C.
D.
?
7.
飞机在空中测得地面上某观测目标的俯角为,且飞机与目标相距千米,那么这时飞机离地面的高度为(
)
A.
B.
C.
D.
?8.
如图,测量河宽(假设河的两岸平行),在点测得,点测得,又,则河宽为(
)
A.米
B.米
C.米
D.米
?
9.
如图,已知灯塔方圆一定范围内有镭射辅助信号,一艘轮船在海上从南向北方向以一定的速度匀速航行,轮船在处测得灯塔在北偏东方向,行驶小时后到达处,此时刚好进入灯塔的镭射信号区,测得灯塔在北偏东方向,则轮船通过灯塔的镭射信号区的时间为(
)
A.小时
B.小时
C.小时
D.小时
?
10.
如图,学校在小明家北偏西方向,且距小明家千米,那么学校所在位置点坐标为(
)
A.
B.
C.
D.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
如图,一个山坡的坡长=米,铅直高度=米,则坡角的大小为________.(用科学计算器计算,结果精确到)
?12.
如图,身高的小丽用一个两锐角分别为和的三角尺测量一棵树的高度,已知她与树之间的距离为,那么这棵树高为(其中小丽眼睛距离地面高度近似为身高)________.
?13.
有一拦水坝的横断面是等腰梯形,它的上底长为,下底长为,高为,则此拦水坝斜坡的坡度为________.
?
14.
如图,一轮船由南向北航行到处时,发现与轮船相距海里的岛在北偏东方向.已知岛周围海里水域有暗礁,如果不改变航向,轮船________(填“有”或“没有”)触暗礁的危险.(可使用科学记算器)
?
15.
若地面上的甲看到高山上乙的仰角为,则乙看到甲的俯角为________度.
?
16.
某建筑物上有一旗杆,由距的处观察旗杆顶部的仰角为,观察底部的仰角为,则旗杆的高度________(精确到).
?17.
如图,要在宽为米的瓯海大道两边安装路灯,路灯的灯臂与灯柱成角,灯罩的轴线与灯臂垂直,当灯罩的轴线通过公路路面的中心线(即为的中点)时照明效果最佳,若米,则路灯的灯柱高度应该设计为________米.(计算结果保留根号).
?18.
如图,小华站在河岸上的点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船的俯角是=,若小华的眼睛与地面的距离是米,=米,平行于所在的直线,迎水坡=,坡长=米,点、、、、、在同一平面内,则此时小船到岸边的距离的长为________米.(结果保留根号)
?19.
如图,一根电线杆的接线柱部分在阳光下的投影的长为米,太阳光线与地面的夹角=,则的长为________米.
?20.
如图,客轮在海上以的速度由向航行,在处测得灯塔的方位角为北偏东,测得处的方位角为南偏东.航行后到达处,在处测得灯塔的方位角为北偏东,则到的距离是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
已知电线杆直立于地面,它的影子恰好照在土坡的坡面和地面上.如果与地面成,,米,米,求电线杆的长.
?
22.
如图,甲楼的底端处与乙楼的底端处相距,从甲楼顶部处看乙楼顶部处的仰角的度数为.从甲楼顶部处看乙楼底部处的俯角的度数为.分别求甲楼和乙楼的高为多少(精确到).(参考数据:,,,,,)
?
23.
如图,海上有一灯塔,在它周围海里内有暗礁.一艘海轮以海里/时的速度由西向东方向航行,行至点处测得灯塔在它的北偏东的方向上,继续向东行驶分钟后,到达处又测得灯塔在它的北偏东方向上,如果海轮不改变方向继续前进有没有触礁的危险?
?
24.
如图,道路边有一棵树,身高米的某人站在水平地面的点处,从点测得树的顶端点的仰角为,树的底部点的俯角为,求树的高度.
?
25.
如图,小芳站在地面上处放风筝,风筝飞到处时的线长为米,这时测得,牵引底端与地面的距离为米,求此时风筝离地面的高度.(结果精确到米)(参考数据:,,)
?
26.
如图,小明设计了一个“简易量角器”:在中,,,,在边上有一系列点,,,使得,,,….
(1)连接,求的度数;
(2)求线段的长(结果精确到,参考数据:,,).
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:如图,过点作于点.
由题意得,(海里),.
在直角中,海里.
在直角中,,则,
所以(海里).
故选.
2.
【答案】
C
【解答】
在中,
∵
=米,为,
∴
==(米).
3.
【答案】
C
【解答】
过点作于点,过点作于点,则四边形是矩形
∴
==,==,
在中,,
∵
=,
∴
==,
即==米.
4.
【答案】
B
【解答】
解:如图,∵
在中,,米,,
∴
(米).
又∵
米,
∴
米.
又∵
在直角中,,,
∴
(米)
故选:.
5.
【答案】
D
【解答】
解:过点作于,
由题意得,,
则,
设台风中心距点处,刚好处在上的,两点则,
在中,,,
则,
从而可得:,
故镇受台风严重影响的时间为.
故选.
6.
【答案】
C
【解答】
解:如图,
,
在中,,
在中,,
.
故选:.
7.
【答案】
A
【解答】
解:如图:为飞机离地面的高度,
所以在直角三角形中,,,
则,
故选:.
8.
【答案】
C
【解答】
解:∵
,,
∴
,
∴
,
在中,
.
故选.
9.
【答案】
B
【解答】
解:连接,过点作于.
在中,∵
,
∴
,
在中,∵
,
∴
,
∴
,
∴
:.
故轮船通过灯塔的镭射信号区的时间为小时.
故选.
10.
【答案】
D
【解答】
解:∵
学校在小明家北偏西方向,且距小明家千米,
∴
,.
∵
,
∴
,.
即点坐标为.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
∵
=米,=米,
∴
.
∴
=.
12.
【答案】
【解答】
由题意得:=,
在中,
∴
=,又=
∴
===,
所以树的高度为.
13.
【答案】
【解答】
解:如图,作于,于,
,,.
∵
,,为等腰梯形.
∴
,.
∵
.
坡角.
14.
【答案】
没有
【解答】
解:已知,,
则.
所以轮船没有触暗礁的危险.
15.
【答案】
【解答】
解:若地面上的甲看到高山上乙的仰角为,则乙看到甲的俯角为.
故答案为:
16.
【答案】
【解答】
解:根据题意:在中,有.
在中,有.
∴
(米).
17.
【答案】
【解答】
解:如图,延长,交于点.
∵
,,米,米,
∴
在直角中,米,
(米),
∵
,,
∴
,
∴
,
∴
(米),
∴
(米).
故答案为:.
18.
【答案】
【解答】
过点作于点,延长交于点,得和矩形.
∵
,=米,
∴
,.
∵
=,=,
∴
==,
==.
在中,
∵
==,=,,
∴
=.
又∵
=,
即,
∴
=(米).
19.
【答案】
【解答】
作于,于.
∵
=,=,
∴
=.
在中=,,
∴
=(米).
20.
【答案】
【解答】
解:过点作于点.
在中,∵
,,,
∴
,
在中,∵
,,
∴
,
∴
.
即到的距离为.
故答案为.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:如图,延长交的延长线于点,作于.
∵
在中,,,,
∴
.
∵
在中,,,
∴
,
∴
.
∵
在中,,,
∴
.
故电线杆的长为米.
【解答】
解:如图,延长交的延长线于点,作于.
∵
在中,,,,
∴
.
∵
在中,,,
∴
,
∴
.
∵
在中,,,
∴
.
故电线杆的长为米.
22.
【答案】
甲楼的高约为,乙楼的高约为.
【解答】
解:由题意,得,,,,
在中,,
∴
,
在?中,,
∴
,
∴
.
23.
【答案】
解:过作.
海里.
∵
,
∴
∴
海里.
在直角中,海里.
∵
∴
海轮不改变方向继续前进没有触礁的危险.
【解答】
解:过作.
海里.
∵
,
∴
∴
海里.
在直角中,海里.
∵
∴
海轮不改变方向继续前进没有触礁的危险.
24.
【答案】
树的高度为.
【解答】
解:在中,
∵
,,
∴
,
在中,∵
,∴
,
25.
【答案】
此时风筝离地面的高度约为米.
【解答】
解:在中,(米),
米米米.
26.
【答案】
解:(1)如下图一所示:
∵
在边上有一系列点,,,使得,,,…,
∴
,
∵
,
∴
,
即的度数是;
(2)∵
在中,,,,,
∴
,
∴
,
∵
,,
∴
,
∵
,,
∴
,
即线段的长是.
【解答】
解:(1)如下图一所示:
∵
在边上有一系列点,,,使得,,,…,
∴
,
∵
,
∴
,
即的度数是;
(2)∵
在中,,,,,
∴
,
∴
,
∵
,,
∴
,
∵
,,
∴
,
即线段的长是.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
