苏科版九年级数学下册 第七章 锐角三角函数 单元检测试题(Word版 有答案)
文档属性
| 名称 | 苏科版九年级数学下册 第七章 锐角三角函数 单元检测试题(Word版 有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 178.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览


文档简介
第七章
锐角三角函数
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
在中,,,,则的正切值为?
?
?
?
A.
B.
C.
D.
?
2.
在中,,若,则的值是?
?
?
?
A.
B.
C.
D.
?
3.
若,则的正切值的范围是(
)
A.
B.
C.
D.
?
4.
中,,若,则的长为(?
?
?
?
)
A.
B.
C.
D.
?
5.
已知为锐角,,则=(
)
A.
B.
C.
D.
?
6.
在中,,下列式子中不一定成立的是(?
?
?
?
)
A.
B.
C.
D.
?
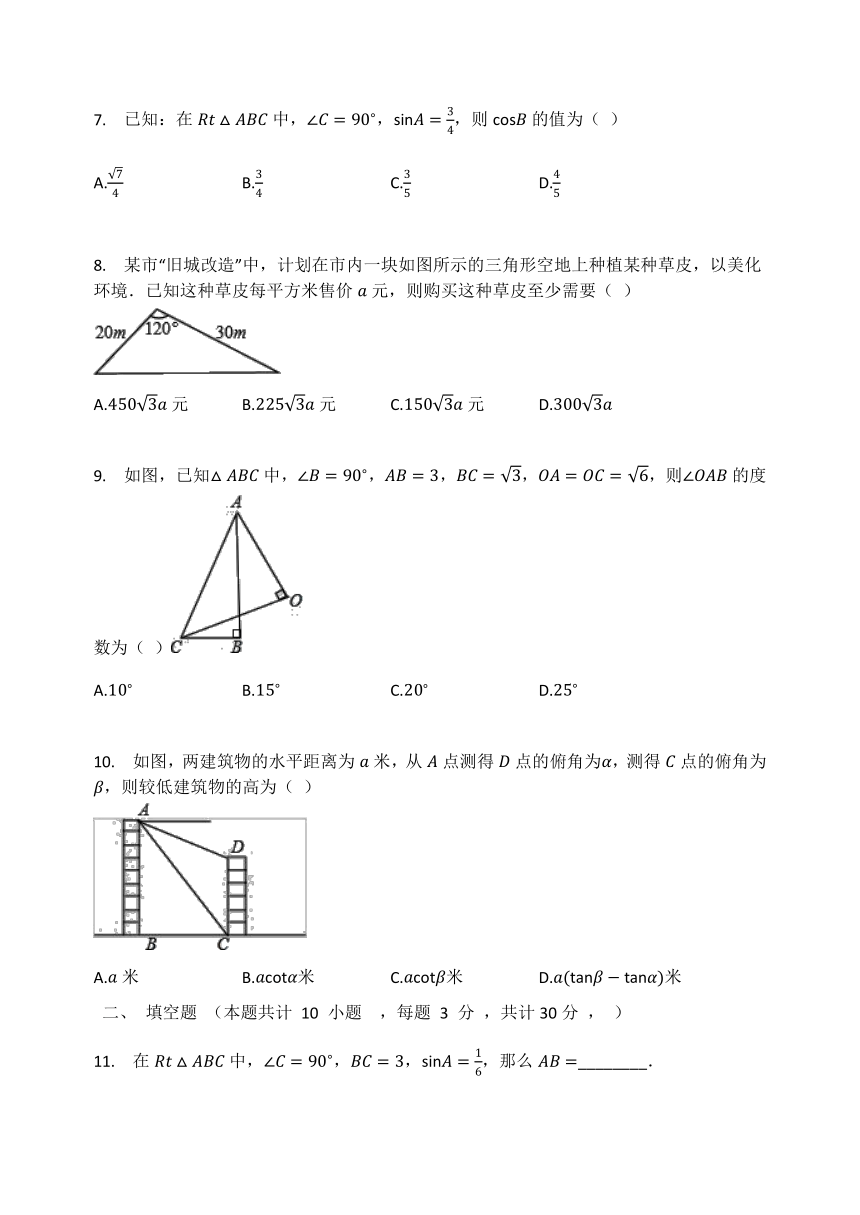
7.
已知:在中,,,则的值为(
)
A.
B.
C.
D.
?
8.
某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价元,则购买这种草皮至少需要(
)
A.元
B.元
C.元
D.
?
9.
如图,已知中,,,,,则的度数为(
)
A.
B.
C.
D.
?
10.
如图,两建筑物的水平距离为米,从点测得点的俯角为,测得点的俯角为,则较低建筑物的高为(
)
A.米
B.米
C.米
D.米
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
在中,,,,那么________.
?
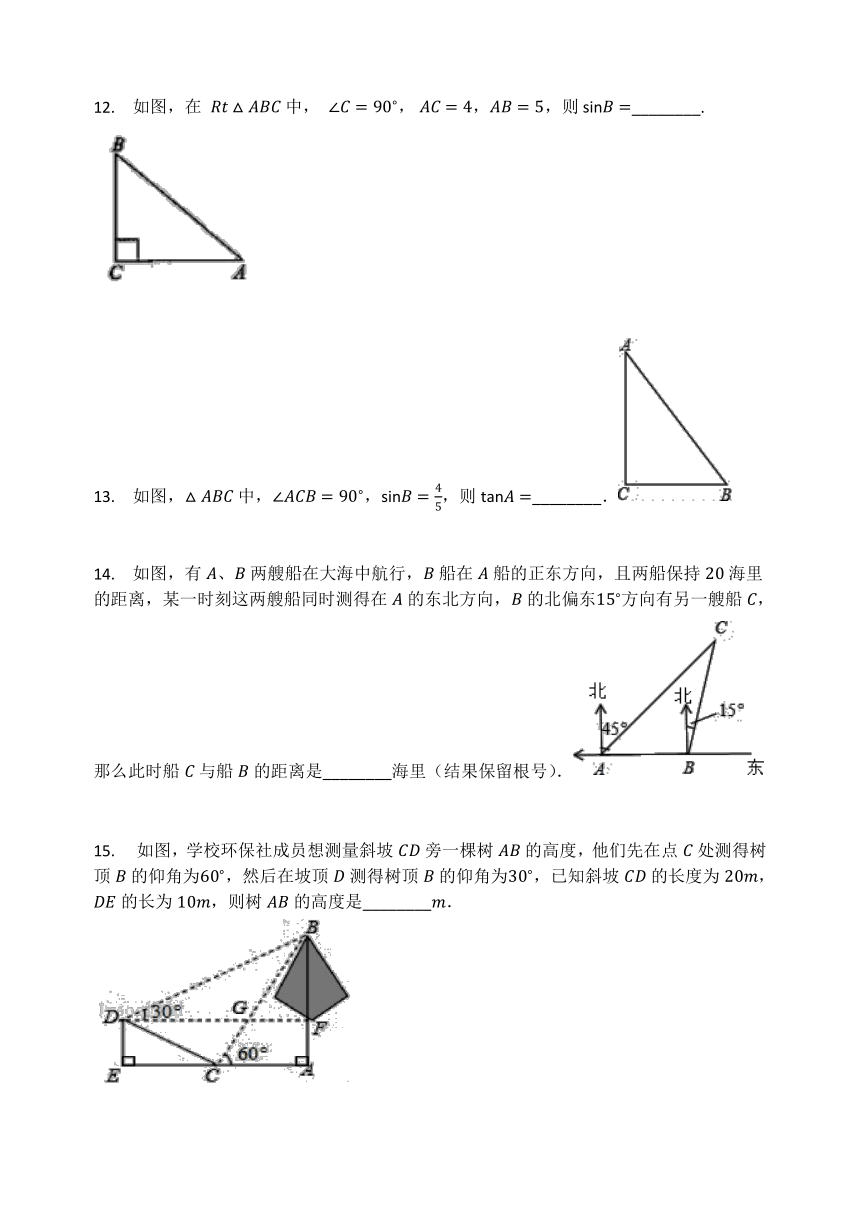
12.
如图,在
中,
,?,,则?________.
?
13.
如图,中,,,则________.
?
14.
如图,有、两艘船在大海中航行,船在船的正东方向,且两船保持海里的距离,某一时刻这两艘船同时测得在的东北方向,的北偏东方向有另一艘船,那么此时船与船的距离是________海里(结果保留根号).
?
15.
?如图,学校环保社成员想测量斜坡旁一棵树的高度,他们先在点处测得树顶的仰角为,然后在坡顶测得树顶的仰角为,已知斜坡的长度为,的长为,则树的高度是________.
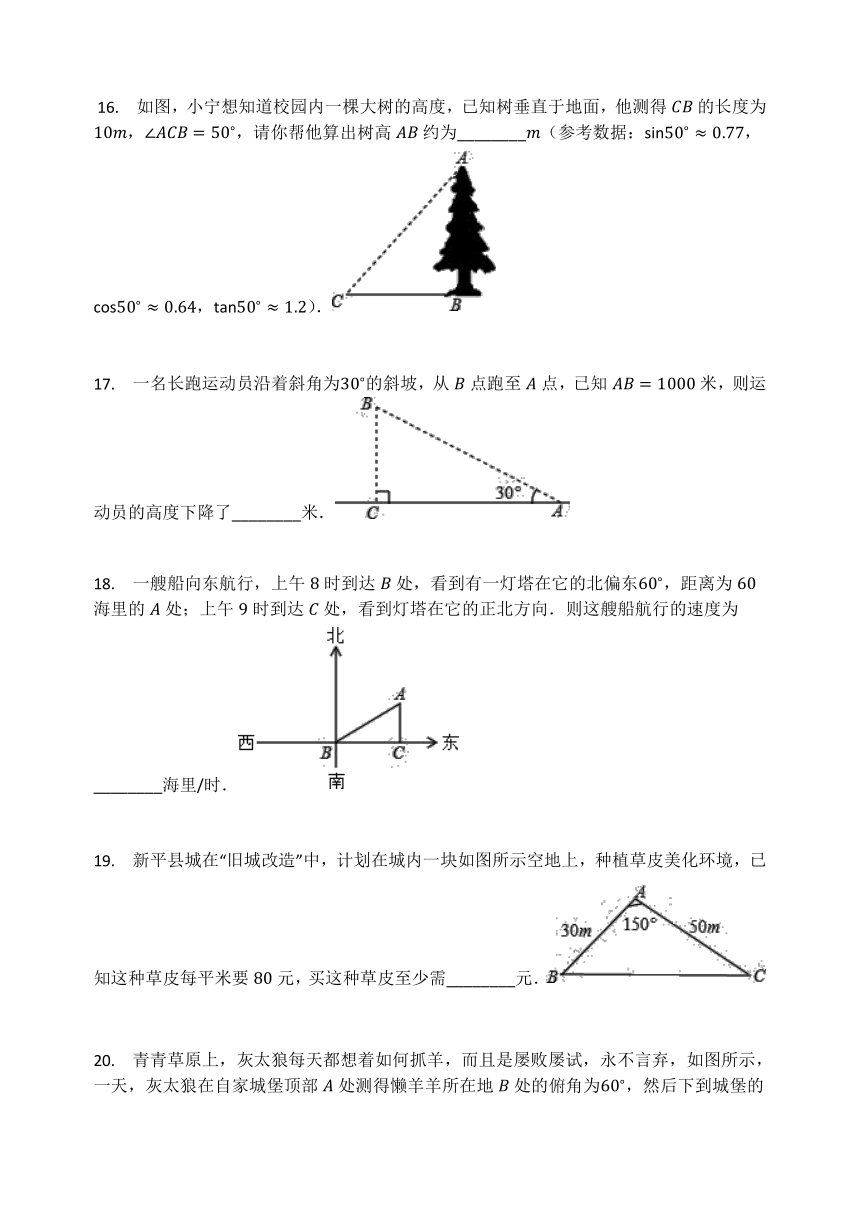
?16.
如图,小宁想知道校园内一棵大树的高度,已知树垂直于地面,他测得的长度为,,请你帮他算出树高约为________(参考数据:,,).
?
17.
一名长跑运动员沿着斜角为的斜坡,从点跑至点,已知米,则运动员的高度下降了________米.
?
18.
一艘船向东航行,上午时到达处,看到有一灯塔在它的北偏东,距离为海里的处;上午时到达处,看到灯塔在它的正北方向.则这艘船航行的速度为________海里/时.
?
19.
新平县城在“旧城改造”中,计划在城内一块如图所示空地上,种植草皮美化环境,已知这种草皮每平米要元,买这种草皮至少需________元.
?
20.
青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃,如图所示,一天,灰太狼在自家城堡顶部处测得懒羊羊所在地处的俯角为,然后下到城堡的处,测得处的俯角为.已知米,若灰太狼以的速度从城堡底部处出发,则至少需________秒钟后能抓到懒羊羊.(结果精确到个位)
三、
解答题
(本题共计
6
小题
,共计60分
,
)
21.
计算:
(1);
(2);
(3);
(4).
?
22.
已知:如图,,、是上的两点,.
(1)求证:;
(2)锐角的正切函数值随角度的增大而________.
?
23.
某学校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动,如图,她在山坡脚处测得这座楼房顶点的仰角为,沿山坡向上走到处再测得点的仰角为,已知,山坡的坡度,且、、在同一条直线上.求:
(1)楼房的高度;
(2)小红在山坡上走过的距离(结果保留根号)
?
24.
在矩形中,点,在边上,米,点在上,米,若,,求的长(精确到个位).
(参考数据:,,,,,)
?
25.
如图,某数学活动小组为测量学校旗杆的高度,从旗杆正前方的处出发,沿斜面坡度的斜坡前进到达处,在处垂直地面放置测量仪,测得旗杆顶部的仰角为.测量仪的高为,求旗杆的高度.
?
26.
某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点处,测得河的南岸边的点在其南偏东方向,然后向北走米到达点,测得点在点的南偏东方向,求出这段河的宽度.(结果精确到米,参考数据:,,,)
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:∵
在中,,,,
∴
的正切值为:.
故选.
2.
【答案】
B
【解答】
解:在中,
∵
,
∴
,
∴
.
∵
,
∴
.
故选.
3.
【答案】
D
【解答】
解:∵
,,一个角的正切值随角的增大而增大,
∴
,
即,
故选.
4.
【答案】
B
【解答】
解:中,,若,
,
∴
.
故选.
5.
【答案】
D
【解答】
∵
为锐角,,
∴
=,
∴
=,
6.
【答案】
D
【解答】
解:根据同角的三角函数的关系:,,,可知只有不正确.
故选.
7.
【答案】
B
【解答】
解:在中,得
.
由一个角的正弦等于它余角的余弦,得
,
故选:.
8.
【答案】
C
【解答】
解:如图,作于点,
在直角中,,
则的面积是.
因而购买这种草皮至少需要元.
故选.
9.
【答案】
B
【解答】
解:∵
,
,
∴
,
∴
,
∵
,
∴
,
在中,
∵
,
∴
,
∴
,
故选.
10.
【答案】
D
【解答】
作于点.
在直角中,==,=
∵
,
∴
==.
同理=.
∴
====.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:在中,
∵
,,
∴
.
故答案为:.
12.
【答案】
【解答】
解:∵
,,,
∴
.
故答案为:.
13.
【答案】
【解答】
解:∵
在中,,
∴
,,.
∵
,
设,则,.
∴
.
14.
【答案】
【解答】
解:过点作于点,
由题意可知:,,
则,
在中,,
在中,.
答:此时船与船的距离是海里.
故答案为.
15.
【答案】
【解答】
解:作于,交于.则四边形是矩形,
∴
,
∵
,
∴
,
∵
,,
∴
,
∴
,
在中,
∵
,
∴
,
∴
,
在和中,
∵
∴
,
∴
,
∴
,
故答案为:.
16.
【答案】
【解答】
解:由题意得出:,
∴
,
∴
,
故答案为:.
17.
【答案】
【解答】
解:在中,
∵
米,,
∴
(米).
故答案为:.
18.
【答案】
【解答】
解:易得,.
∴
(海里).
∴
这艘船航行的速度为(海里/时).
19.
【答案】
【解答】
解:作交的延长线于,
∵
,
∴
,
∵
,
∴
,
∴
,
∴
所需费用为元,
故答案为.
20.
【答案】
【解答】
解:根据题意得:,,
在中,
∵
,
∴
则,
在中,
∵
,
∴
,
即,
解得:,
∴
,
∴
约秒钟后灰太狼能抓到懒羊羊.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:(1)原式
;
(2)原式
;
(3)原式
;
(4)原式
.
【解答】
解:(1)原式
;
(2)原式
;
(3)原式
;
(4)原式
.
22.
【答案】
增大.
【解答】
解:(1)∵
,
∴
和均为直角三角形.
∴
,.
∴
.
(2)由(1)可知锐角的正切函数值随角度的增大而增大.
23.
【答案】
高楼的高度为,小玲在山坡上走过的距离为.
【解答】
解:(1)在中,,.
∵
,
即,
∴
.?
(2)如图,过点作于,于.
则,.
根据题意,知,
可设,.???????????????????????
在中,,
∴
,
即.
∴
.
解得.??????????????????????????
在中,
∵
,
∴
.
∴
.????????????????????
答:高楼的高度为,小玲在山坡上走过的距离为.
24.
【答案】
的长约为米.
【解答】
解:过点作,交于点,过点作,垂足为点,
∵
矩形,
∴
,
∵
米,
∴
米,
∵
米,
∴
米,
∵
,,
∴
,
∴
米,
在中,(米),
25.
【答案】
解:延长交于,过作于,
∵
,
?∴
,
设,则,
∴
,
∴
,
∴
,
,
在中,
,
∴
.
【解答】
解:延长交于,过作于,
∵
,
?∴
,
设,则,
∴
,
∴
,
∴
,
,
在中,
,
∴
.
26.
【答案】
解:如图,记河南岸为,延长交于点,则.
由题意知,,,
设米,则米,米,
在中,,
∴
,
解得.
答:这段河宽约为.
【解答】
解:如图,记河南岸为,延长交于点,则.
由题意知,,,
设米,则米,米,
在中,,
∴
,
解得.
答:这段河宽约为.
锐角三角函数
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
在中,,,,则的正切值为?
?
?
?
A.
B.
C.
D.
?
2.
在中,,若,则的值是?
?
?
?
A.
B.
C.
D.
?
3.
若,则的正切值的范围是(
)
A.
B.
C.
D.
?
4.
中,,若,则的长为(?
?
?
?
)
A.
B.
C.
D.
?
5.
已知为锐角,,则=(
)
A.
B.
C.
D.
?
6.
在中,,下列式子中不一定成立的是(?
?
?
?
)
A.
B.
C.
D.
?
7.
已知:在中,,,则的值为(
)
A.
B.
C.
D.
?
8.
某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价元,则购买这种草皮至少需要(
)
A.元
B.元
C.元
D.
?
9.
如图,已知中,,,,,则的度数为(
)
A.
B.
C.
D.
?
10.
如图,两建筑物的水平距离为米,从点测得点的俯角为,测得点的俯角为,则较低建筑物的高为(
)
A.米
B.米
C.米
D.米
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
在中,,,,那么________.
?
12.
如图,在
中,
,?,,则?________.
?
13.
如图,中,,,则________.
?
14.
如图,有、两艘船在大海中航行,船在船的正东方向,且两船保持海里的距离,某一时刻这两艘船同时测得在的东北方向,的北偏东方向有另一艘船,那么此时船与船的距离是________海里(结果保留根号).
?
15.
?如图,学校环保社成员想测量斜坡旁一棵树的高度,他们先在点处测得树顶的仰角为,然后在坡顶测得树顶的仰角为,已知斜坡的长度为,的长为,则树的高度是________.
?16.
如图,小宁想知道校园内一棵大树的高度,已知树垂直于地面,他测得的长度为,,请你帮他算出树高约为________(参考数据:,,).
?
17.
一名长跑运动员沿着斜角为的斜坡,从点跑至点,已知米,则运动员的高度下降了________米.
?
18.
一艘船向东航行,上午时到达处,看到有一灯塔在它的北偏东,距离为海里的处;上午时到达处,看到灯塔在它的正北方向.则这艘船航行的速度为________海里/时.
?
19.
新平县城在“旧城改造”中,计划在城内一块如图所示空地上,种植草皮美化环境,已知这种草皮每平米要元,买这种草皮至少需________元.
?
20.
青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃,如图所示,一天,灰太狼在自家城堡顶部处测得懒羊羊所在地处的俯角为,然后下到城堡的处,测得处的俯角为.已知米,若灰太狼以的速度从城堡底部处出发,则至少需________秒钟后能抓到懒羊羊.(结果精确到个位)
三、
解答题
(本题共计
6
小题
,共计60分
,
)
21.
计算:
(1);
(2);
(3);
(4).
?
22.
已知:如图,,、是上的两点,.
(1)求证:;
(2)锐角的正切函数值随角度的增大而________.
?
23.
某学校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动,如图,她在山坡脚处测得这座楼房顶点的仰角为,沿山坡向上走到处再测得点的仰角为,已知,山坡的坡度,且、、在同一条直线上.求:
(1)楼房的高度;
(2)小红在山坡上走过的距离(结果保留根号)
?
24.
在矩形中,点,在边上,米,点在上,米,若,,求的长(精确到个位).
(参考数据:,,,,,)
?
25.
如图,某数学活动小组为测量学校旗杆的高度,从旗杆正前方的处出发,沿斜面坡度的斜坡前进到达处,在处垂直地面放置测量仪,测得旗杆顶部的仰角为.测量仪的高为,求旗杆的高度.
?
26.
某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点处,测得河的南岸边的点在其南偏东方向,然后向北走米到达点,测得点在点的南偏东方向,求出这段河的宽度.(结果精确到米,参考数据:,,,)
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:∵
在中,,,,
∴
的正切值为:.
故选.
2.
【答案】
B
【解答】
解:在中,
∵
,
∴
,
∴
.
∵
,
∴
.
故选.
3.
【答案】
D
【解答】
解:∵
,,一个角的正切值随角的增大而增大,
∴
,
即,
故选.
4.
【答案】
B
【解答】
解:中,,若,
,
∴
.
故选.
5.
【答案】
D
【解答】
∵
为锐角,,
∴
=,
∴
=,
6.
【答案】
D
【解答】
解:根据同角的三角函数的关系:,,,可知只有不正确.
故选.
7.
【答案】
B
【解答】
解:在中,得
.
由一个角的正弦等于它余角的余弦,得
,
故选:.
8.
【答案】
C
【解答】
解:如图,作于点,
在直角中,,
则的面积是.
因而购买这种草皮至少需要元.
故选.
9.
【答案】
B
【解答】
解:∵
,
,
∴
,
∴
,
∵
,
∴
,
在中,
∵
,
∴
,
∴
,
故选.
10.
【答案】
D
【解答】
作于点.
在直角中,==,=
∵
,
∴
==.
同理=.
∴
====.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:在中,
∵
,,
∴
.
故答案为:.
12.
【答案】
【解答】
解:∵
,,,
∴
.
故答案为:.
13.
【答案】
【解答】
解:∵
在中,,
∴
,,.
∵
,
设,则,.
∴
.
14.
【答案】
【解答】
解:过点作于点,
由题意可知:,,
则,
在中,,
在中,.
答:此时船与船的距离是海里.
故答案为.
15.
【答案】
【解答】
解:作于,交于.则四边形是矩形,
∴
,
∵
,
∴
,
∵
,,
∴
,
∴
,
在中,
∵
,
∴
,
∴
,
在和中,
∵
∴
,
∴
,
∴
,
故答案为:.
16.
【答案】
【解答】
解:由题意得出:,
∴
,
∴
,
故答案为:.
17.
【答案】
【解答】
解:在中,
∵
米,,
∴
(米).
故答案为:.
18.
【答案】
【解答】
解:易得,.
∴
(海里).
∴
这艘船航行的速度为(海里/时).
19.
【答案】
【解答】
解:作交的延长线于,
∵
,
∴
,
∵
,
∴
,
∴
,
∴
所需费用为元,
故答案为.
20.
【答案】
【解答】
解:根据题意得:,,
在中,
∵
,
∴
则,
在中,
∵
,
∴
,
即,
解得:,
∴
,
∴
约秒钟后灰太狼能抓到懒羊羊.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:(1)原式
;
(2)原式
;
(3)原式
;
(4)原式
.
【解答】
解:(1)原式
;
(2)原式
;
(3)原式
;
(4)原式
.
22.
【答案】
增大.
【解答】
解:(1)∵
,
∴
和均为直角三角形.
∴
,.
∴
.
(2)由(1)可知锐角的正切函数值随角度的增大而增大.
23.
【答案】
高楼的高度为,小玲在山坡上走过的距离为.
【解答】
解:(1)在中,,.
∵
,
即,
∴
.?
(2)如图,过点作于,于.
则,.
根据题意,知,
可设,.???????????????????????
在中,,
∴
,
即.
∴
.
解得.??????????????????????????
在中,
∵
,
∴
.
∴
.????????????????????
答:高楼的高度为,小玲在山坡上走过的距离为.
24.
【答案】
的长约为米.
【解答】
解:过点作,交于点,过点作,垂足为点,
∵
矩形,
∴
,
∵
米,
∴
米,
∵
米,
∴
米,
∵
,,
∴
,
∴
米,
在中,(米),
25.
【答案】
解:延长交于,过作于,
∵
,
?∴
,
设,则,
∴
,
∴
,
∴
,
,
在中,
,
∴
.
【解答】
解:延长交于,过作于,
∵
,
?∴
,
设,则,
∴
,
∴
,
∴
,
,
在中,
,
∴
.
26.
【答案】
解:如图,记河南岸为,延长交于点,则.
由题意知,,,
设米,则米,米,
在中,,
∴
,
解得.
答:这段河宽约为.
【解答】
解:如图,记河南岸为,延长交于点,则.
由题意知,,,
设米,则米,米,
在中,,
∴
,
解得.
答:这段河宽约为.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
