人教版 八年级上册数学 11.3 多边形及其内角和 同步训练(word解析版)
文档属性
| 名称 | 人教版 八年级上册数学 11.3 多边形及其内角和 同步训练(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 244.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 08:56:11 | ||
图片预览


文档简介
人教版
八年级数学
11.3
多边形及其内角和
同步训练
一、选择题(本大题共10道小题)
1.
若正多边形的内角和是540°,则该正多边形的一个外角为
A.45°
B.60°
C.72°
D.90°
2.
八边形的内角和等于( )
A.360°
B.1080°
C.1440°
D.2160°
3.
从九边形的一个顶点出发可以引出的对角线的条数为( )
A.3
B.4
C.6
D.9
4.
如图,足球图片正中的黑色正五边形的内角和是
A.180°
B.360°
C.540°
D.720°
5.
若一个正多边形的每一个外角都等于40°,则它是( )
A.正九边形
B.正十边形
C.正十一边形
D.正十二边形
6.
若一个多边形的一个顶点处的所有对角线把多边形分成4个三角形,则这个多边形的边数为( )
A.3
B.4
C.5
D.6
7.
下列哪一个度数可以作为某一个多边形的内角和
( )
A.240°
B.600°
C.540°
D.2180°
8.
一个正多边形的每个外角不可能等于( )
A.30°
B.50°
C.40°
D.60°
9.
一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7
B.7或8
C.8或9
D.7或8或9
10.
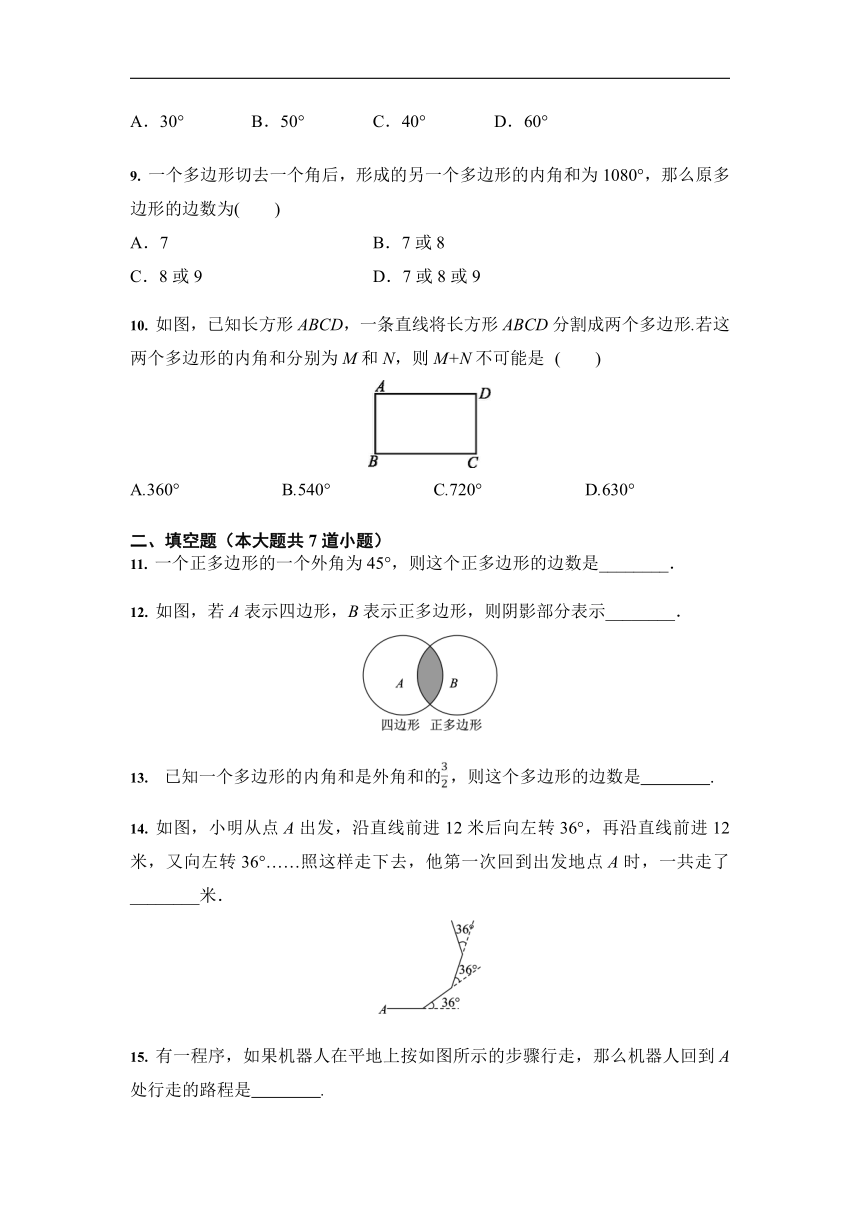
如图,已知长方形ABCD,一条直线将长方形ABCD分割成两个多边形.若这两个多边形的内角和分别为M和N,则M+N不可能是
( )
A.360°
B.540°
C.720°
D.630°
二、填空题(本大题共7道小题)
11.
一个正多边形的一个外角为45°,则这个正多边形的边数是________.
12.
如图,若A表示四边形,B表示正多边形,则阴影部分表示________.
13.
已知一个多边形的内角和是外角和的,则这个多边形的边数是 .
?
14.
如图,小明从点A出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°……照这样走下去,他第一次回到出发地点A时,一共走了________米.
15.
有一程序,如果机器人在平地上按如图所示的步骤行走,那么机器人回到A处行走的路程是 .?
16.
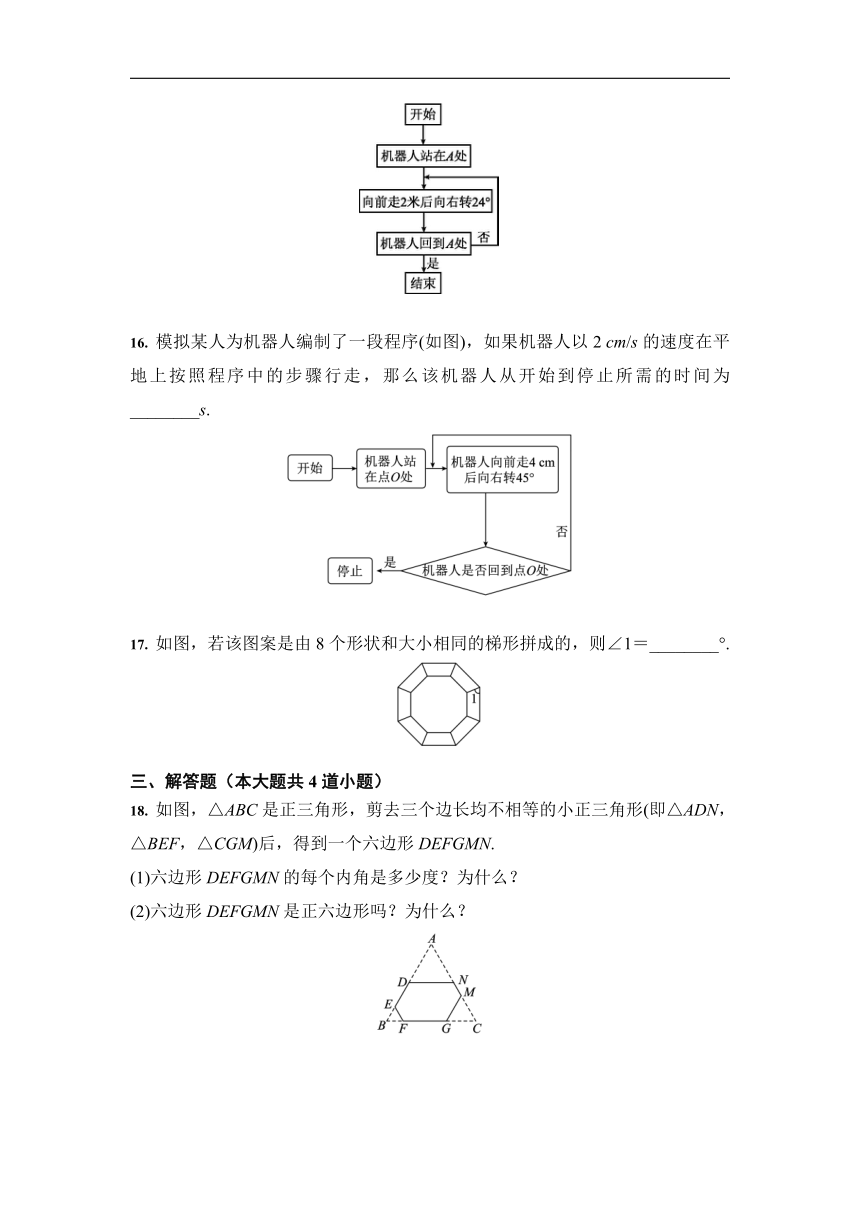
模拟某人为机器人编制了一段程序(如图),如果机器人以2
cm/s的速度在平地上按照程序中的步骤行走,那么该机器人从开始到停止所需的时间为________s.
17.
如图,若该图案是由8个形状和大小相同的梯形拼成的,则∠1=________°.
三、解答题(本大题共4道小题)
18.
如图,△ABC是正三角形,剪去三个边长均不相等的小正三角形(即△ADN,△BEF,△CGM)后,得到一个六边形DEFGMN.
(1)六边形DEFGMN的每个内角是多少度?为什么?
(2)六边形DEFGMN是正六边形吗?为什么?
19.
某单位修建正多边形花台,已知正多边形花台的一个外角的度数比一个内角度数的多12°.
(1)求出这个正多边形的一个内角的度数;
(2)求这个正多边形的边数.
20.
小华与小明在讨论一个凸多边形的问题,他们的对话如下:
小华说:“这个凸多边形的内角和是2020°.”
小明说:“不可能吧!你错把一个外角当作内角了!”
请根据俩人的对话,回答下列问题:
(1)凸多边形的内角和为2020°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
21.
如图,在五边形ABCDE中,∠A+∠B+∠E=310°,CF平分∠DCB,CF的反向延长线与∠EDC处的外角的平分线相交于点P,求∠P的度数.
人教版
八年级数学
11.3
多边形及其内角和
同步训练-答案
一、选择题(本大题共10道小题)
1.
【答案】C
【解析】∵正多边形的内角和是540°,
∴多边形的边数为540°÷180°+2=5,
∵多边形的外角和都是360°,
∴多边形的每个外角=360÷5=72°.
故选C.
2.
【答案】B
3.
【答案】C [解析]
从九边形的一个顶点出发,可以向与这个顶点不相邻的6个顶点引对角线,即能引出6条对角线.
4.
【答案】C
【解析】黑色正五边形的内角和为:(5–2)×180°=540°,
故选C.
5.
【答案】A [解析]
由于正多边形的外角和为360°,且每一个外角都相等,因此边数==9.
6.
【答案】D [解析]
设这个多边形的边数为n,则n-2=4,解得n=6.
7.
【答案】C [解析]
∵多边形内角和公式为(n-2)×180°,
∴多边形内角和一定是180°的倍数.
∵540°=3×180°,
∴540°可以作为某一个多边形的内角和.
8.
【答案】B [解析]
设正多边形的边数为n,则当30°n=360°时,n=12,故A可能;当50°n=360°时,n=,不是整数,故B不可能;当40°n=360°时,n=9,故C可能;当60°n=360°时,n=6,故D可能.
9.
【答案】D [解析]
设内角和为1080°的多边形的边数为n,则(n-2)×180°=1080°,解得n=8.则原多边形的边数为7或8或9.故选D.
10.
【答案】D [解析]
一条直线将长方形ABCD分割成两个多边形的情况有以下三种:
(1)直线不经过原长方形的顶点,如图①②,此时长方形被分割为一个五边形和一个三角形或两个四边形,
∴M+N=540°+180°=720°或M+N=360°+360°=720°;
(2)直线经过原长方形的一个顶点,如图③,此时长方形被分割为一个四边形和一个三角形,
∴M+N=360°+180°=540°;
(3)直线经过原长方形的两个顶点,如图④,此时长方形被分割为两个三角形,
∴M+N=180°+180°=360°.
二、填空题(本大题共7道小题)
11.
【答案】8 【解析】由正多边形的每一个外角都是45°,其外角和为360°,可得这个正多边形的边数是=8.
【一题多解】因为正多边形的每一个外角都是45°,所以这个正多边形的每一个内角都是180°-45°=135°,设正多边形的边数为n,则(n-2)×180°=135°×n,解得n=8.
设正多边形的边数为n,正多边形的外角和为360°,内角和为(n-2)×180°,每个内角的度数为.
12.
【答案】正方形
13.
【答案】
5
14.
【答案】120 [解析]
由题意得360°÷36°=10,
则他第一次回到出发地点A时,一共走了12×10=120(米).故答案为120.
15.
【答案】30米 [解析]
360°÷24°=15,利用多边形的外角和等于360°,可知机器人回到A处时,恰好沿着正十五边形的边走了一圈,即可求得路程为15×2=30(米).
16.
【答案】16 [解析]
由题意得,该机器人所经过的路径是一个正多边形,
多边形的边数为=8,
则所走的路程是4×8=32(cm),
故所用的时间是32÷2=16(s).
17.
【答案】67.5
三、解答题(本大题共4道小题)
18.
【答案】
解:(1)六边形DEFGMN的各个内角都是120°.
理由:∵△ADN,△BEF,△CGM都是正三角形,
∴它们的每个内角都是60°,即六边形DEFGMN的每个外角都是60°.
∴六边形DEFGMN的每个内角都是120°.
(2)六边形DEFGMN不是正六边形.
理由:∵三个小正三角形(即△ADN,△BEF,△CGM)的边长均不相等,
∴DN,EF,GM均不相等.
∴六边形DEFGMN不是正六边形.
19.
【答案】
解:(1)设这个多边形的一个内角的度数是x°,则与其相邻的外角度数是x°+12°.
由题意,得x+x+12=180,解得x=140.
即这个正多边形的一个内角的度数是140°.
(2)这个正多边形的每一个外角的度数为180°-140°=40°,所以这个正多边形的边数是=9.
20.
【答案】
解:(1)∵n边形的内角和是(n-2)×180°,
∴多边形的内角和一定是180°的整倍数.
∵2020÷180=11……40,
∴多边形的内角和不可能为2020°.
(2)设小华求的是n边形的内角和,这个内角为x°,则0<x<180.
根据题意,得(n-2)×180°-x+(180°-x)=2020°,解得n=12+.
∵n为正整数,
∴2x+40必为180的整倍数.
又∵0<x<180,
∴<<.
∴n=13或14.
∴小华求的是十三边形或十四边形的内角和.
21.
【答案】
解:延长ED,BC相交于点G.
在四边形ABGE中,∠G=360°-(∠A+∠B+∠E)=50°,
∠P=∠FCD-∠CDP=(∠DCB-∠CDG)=∠G=×50°=25°.
八年级数学
11.3
多边形及其内角和
同步训练
一、选择题(本大题共10道小题)
1.
若正多边形的内角和是540°,则该正多边形的一个外角为
A.45°
B.60°
C.72°
D.90°
2.
八边形的内角和等于( )
A.360°
B.1080°
C.1440°
D.2160°
3.
从九边形的一个顶点出发可以引出的对角线的条数为( )
A.3
B.4
C.6
D.9
4.
如图,足球图片正中的黑色正五边形的内角和是
A.180°
B.360°
C.540°
D.720°
5.
若一个正多边形的每一个外角都等于40°,则它是( )
A.正九边形
B.正十边形
C.正十一边形
D.正十二边形
6.
若一个多边形的一个顶点处的所有对角线把多边形分成4个三角形,则这个多边形的边数为( )
A.3
B.4
C.5
D.6
7.
下列哪一个度数可以作为某一个多边形的内角和
( )
A.240°
B.600°
C.540°
D.2180°
8.
一个正多边形的每个外角不可能等于( )
A.30°
B.50°
C.40°
D.60°
9.
一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7
B.7或8
C.8或9
D.7或8或9
10.
如图,已知长方形ABCD,一条直线将长方形ABCD分割成两个多边形.若这两个多边形的内角和分别为M和N,则M+N不可能是
( )
A.360°
B.540°
C.720°
D.630°
二、填空题(本大题共7道小题)
11.
一个正多边形的一个外角为45°,则这个正多边形的边数是________.
12.
如图,若A表示四边形,B表示正多边形,则阴影部分表示________.
13.
已知一个多边形的内角和是外角和的,则这个多边形的边数是 .
?
14.
如图,小明从点A出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°……照这样走下去,他第一次回到出发地点A时,一共走了________米.
15.
有一程序,如果机器人在平地上按如图所示的步骤行走,那么机器人回到A处行走的路程是 .?
16.
模拟某人为机器人编制了一段程序(如图),如果机器人以2
cm/s的速度在平地上按照程序中的步骤行走,那么该机器人从开始到停止所需的时间为________s.
17.
如图,若该图案是由8个形状和大小相同的梯形拼成的,则∠1=________°.
三、解答题(本大题共4道小题)
18.
如图,△ABC是正三角形,剪去三个边长均不相等的小正三角形(即△ADN,△BEF,△CGM)后,得到一个六边形DEFGMN.
(1)六边形DEFGMN的每个内角是多少度?为什么?
(2)六边形DEFGMN是正六边形吗?为什么?
19.
某单位修建正多边形花台,已知正多边形花台的一个外角的度数比一个内角度数的多12°.
(1)求出这个正多边形的一个内角的度数;
(2)求这个正多边形的边数.
20.
小华与小明在讨论一个凸多边形的问题,他们的对话如下:
小华说:“这个凸多边形的内角和是2020°.”
小明说:“不可能吧!你错把一个外角当作内角了!”
请根据俩人的对话,回答下列问题:
(1)凸多边形的内角和为2020°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
21.
如图,在五边形ABCDE中,∠A+∠B+∠E=310°,CF平分∠DCB,CF的反向延长线与∠EDC处的外角的平分线相交于点P,求∠P的度数.
人教版
八年级数学
11.3
多边形及其内角和
同步训练-答案
一、选择题(本大题共10道小题)
1.
【答案】C
【解析】∵正多边形的内角和是540°,
∴多边形的边数为540°÷180°+2=5,
∵多边形的外角和都是360°,
∴多边形的每个外角=360÷5=72°.
故选C.
2.
【答案】B
3.
【答案】C [解析]
从九边形的一个顶点出发,可以向与这个顶点不相邻的6个顶点引对角线,即能引出6条对角线.
4.
【答案】C
【解析】黑色正五边形的内角和为:(5–2)×180°=540°,
故选C.
5.
【答案】A [解析]
由于正多边形的外角和为360°,且每一个外角都相等,因此边数==9.
6.
【答案】D [解析]
设这个多边形的边数为n,则n-2=4,解得n=6.
7.
【答案】C [解析]
∵多边形内角和公式为(n-2)×180°,
∴多边形内角和一定是180°的倍数.
∵540°=3×180°,
∴540°可以作为某一个多边形的内角和.
8.
【答案】B [解析]
设正多边形的边数为n,则当30°n=360°时,n=12,故A可能;当50°n=360°时,n=,不是整数,故B不可能;当40°n=360°时,n=9,故C可能;当60°n=360°时,n=6,故D可能.
9.
【答案】D [解析]
设内角和为1080°的多边形的边数为n,则(n-2)×180°=1080°,解得n=8.则原多边形的边数为7或8或9.故选D.
10.
【答案】D [解析]
一条直线将长方形ABCD分割成两个多边形的情况有以下三种:
(1)直线不经过原长方形的顶点,如图①②,此时长方形被分割为一个五边形和一个三角形或两个四边形,
∴M+N=540°+180°=720°或M+N=360°+360°=720°;
(2)直线经过原长方形的一个顶点,如图③,此时长方形被分割为一个四边形和一个三角形,
∴M+N=360°+180°=540°;
(3)直线经过原长方形的两个顶点,如图④,此时长方形被分割为两个三角形,
∴M+N=180°+180°=360°.
二、填空题(本大题共7道小题)
11.
【答案】8 【解析】由正多边形的每一个外角都是45°,其外角和为360°,可得这个正多边形的边数是=8.
【一题多解】因为正多边形的每一个外角都是45°,所以这个正多边形的每一个内角都是180°-45°=135°,设正多边形的边数为n,则(n-2)×180°=135°×n,解得n=8.
设正多边形的边数为n,正多边形的外角和为360°,内角和为(n-2)×180°,每个内角的度数为.
12.
【答案】正方形
13.
【答案】
5
14.
【答案】120 [解析]
由题意得360°÷36°=10,
则他第一次回到出发地点A时,一共走了12×10=120(米).故答案为120.
15.
【答案】30米 [解析]
360°÷24°=15,利用多边形的外角和等于360°,可知机器人回到A处时,恰好沿着正十五边形的边走了一圈,即可求得路程为15×2=30(米).
16.
【答案】16 [解析]
由题意得,该机器人所经过的路径是一个正多边形,
多边形的边数为=8,
则所走的路程是4×8=32(cm),
故所用的时间是32÷2=16(s).
17.
【答案】67.5
三、解答题(本大题共4道小题)
18.
【答案】
解:(1)六边形DEFGMN的各个内角都是120°.
理由:∵△ADN,△BEF,△CGM都是正三角形,
∴它们的每个内角都是60°,即六边形DEFGMN的每个外角都是60°.
∴六边形DEFGMN的每个内角都是120°.
(2)六边形DEFGMN不是正六边形.
理由:∵三个小正三角形(即△ADN,△BEF,△CGM)的边长均不相等,
∴DN,EF,GM均不相等.
∴六边形DEFGMN不是正六边形.
19.
【答案】
解:(1)设这个多边形的一个内角的度数是x°,则与其相邻的外角度数是x°+12°.
由题意,得x+x+12=180,解得x=140.
即这个正多边形的一个内角的度数是140°.
(2)这个正多边形的每一个外角的度数为180°-140°=40°,所以这个正多边形的边数是=9.
20.
【答案】
解:(1)∵n边形的内角和是(n-2)×180°,
∴多边形的内角和一定是180°的整倍数.
∵2020÷180=11……40,
∴多边形的内角和不可能为2020°.
(2)设小华求的是n边形的内角和,这个内角为x°,则0<x<180.
根据题意,得(n-2)×180°-x+(180°-x)=2020°,解得n=12+.
∵n为正整数,
∴2x+40必为180的整倍数.
又∵0<x<180,
∴<<.
∴n=13或14.
∴小华求的是十三边形或十四边形的内角和.
21.
【答案】
解:延长ED,BC相交于点G.
在四边形ABGE中,∠G=360°-(∠A+∠B+∠E)=50°,
∠P=∠FCD-∠CDP=(∠DCB-∠CDG)=∠G=×50°=25°.
