沪教版(上海)初中数学九年级第一学期 25.1(2)锐角三角比的意义 教案
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 25.1(2)锐角三角比的意义 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 67.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览

文档简介
25.1(2)锐角三角比的意义
教学目标:
类比正切、余切概念的形成过程得到一个锐角的正弦与余弦的定义以及锐角三角比的定义。能熟练运用锐角三角比的概念进行有关计算。掌握直角三角形锐角三角比及其值的取值范围;在学习过程中培养学生分析问题解决问题的能力及学习数学的兴趣。
教学重点:理解余弦、正弦的概念;熟练运用锐角三角比的概念进行有关计算。
教学难点:灵活应用锐角三角比解决问题
教学过程:
教学环节
教学过程
设计意图
一、
回
顾
旧
知
上节课我们学了在直角三角形中一个锐角的对边与邻边之间的关系。
1.∠A的正切:tanA=
2.∠A的余切:cotA=
思考:我们是怎么说明一个锐角的对边与邻边的比值是一个定值的?
巩固正切、余切概念,并回忆上节课内容的证法,为本节课做铺垫。
二、
探
索
新
知
1、讨论:
在直角三角形中,当锐角A确定时,邻边与对边的比值随之确定外,还有其他两边之间的比值是确定的吗?
请学生用学过的知识说明。
先小组讨论,然后交流。
2、归纳:
(1)、∠A的对边和斜边的比值是确定的。
(2)、∠A的邻边和斜边的比值是确定的。
3、引出概念
(1)在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正弦.记作sinA.
sinA=
(2)在Rt△ABC中,∠C=90°,我们把锐角A的邻边与对边的比叫做∠A的余弦.记作cosA.
cosA=;
(3)一个锐角的正切、余切、正弦、余弦统称为这个锐角三角比。
借助于上节课的知识发挥学生的主观能动性,探讨正弦、余弦的概念,并培养学生团结协作的精神。
三、
应
用
新
知
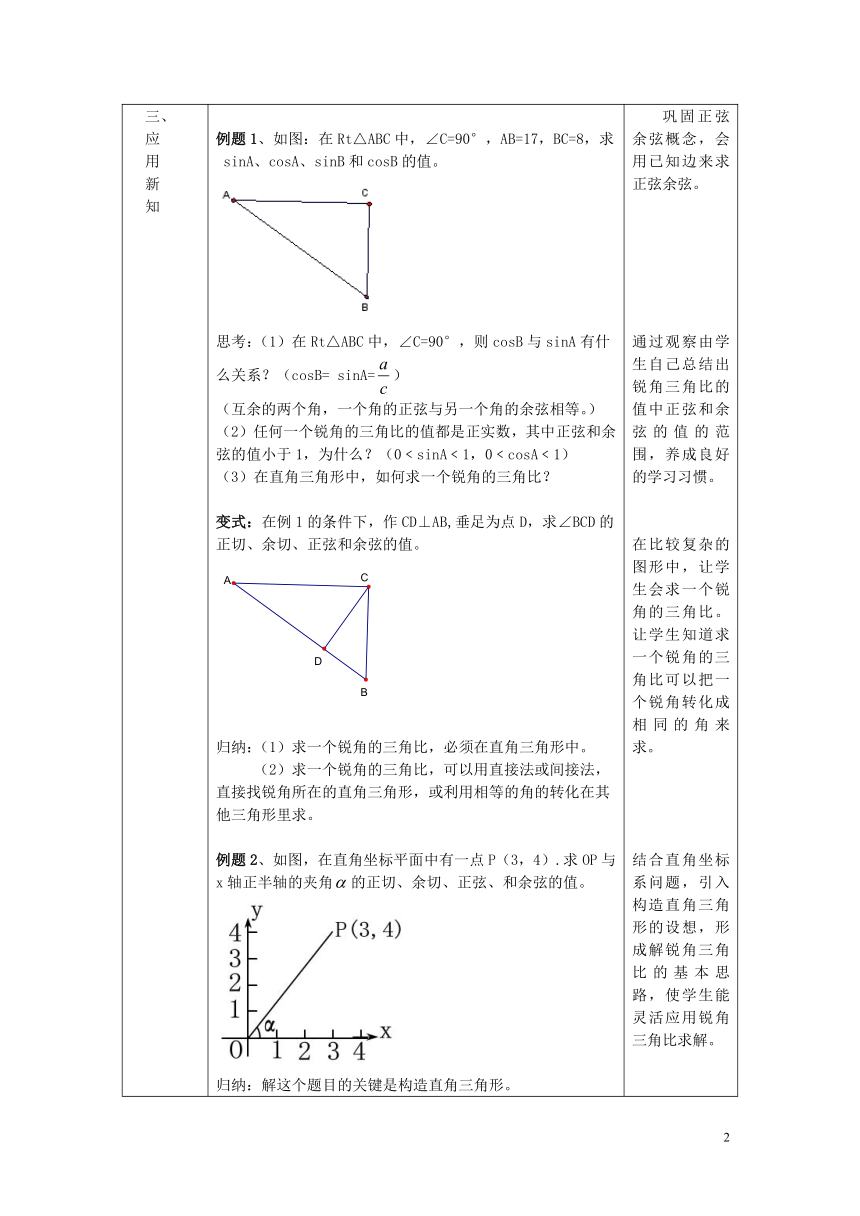
例题1、如图:在Rt△ABC中,∠C=90°,AB=17,BC=8,求sinA、cosA、sinB和cosB的值。
思考:(1)在Rt△ABC中,∠C=90°,则cosB与sinA有什么关系?(cosB=
sinA=)
(互余的两个角,一个角的正弦与另一个角的余弦相等。)
(2)任何一个锐角的三角比的值都是正实数,其中正弦和余弦的值小于1,为什么?(0﹤sinA﹤1,0﹤cosA﹤1)
(3)在直角三角形中,如何求一个锐角的三角比?
变式:在例1的条件下,作CD⊥AB,垂足为点D,求∠BCD的正切、余切、正弦和余弦的值。
归纳:(1)求一个锐角的三角比,必须在直角三角形中。
(2)求一个锐角的三角比,可以用直接法或间接法,直接找锐角所在的直角三角形,或利用相等的角的转化在其他三角形里求。
例题2、如图,在直角坐标平面中有一点P(3,4).求OP与x轴正半轴的夹角的正切、余切、正弦、和余弦的值。
归纳:解这个题目的关键是构造直角三角形。
变式:当点P是正比例函数在第一象限的一个点,你能求出OP与x轴正半轴的夹角的正切、余切、正弦、和余弦的值吗?
巩固正弦余弦概念,会用已知边来求正弦余弦。
通过观察由学生自己总结出锐角三角比的值中正弦和余弦的值的范围,养成良好的学习习惯。
在比较复杂的图形中,让学生会求一个锐角的三角比。让学生知道求一个锐角的三角比可以把一个锐角转化成相同的角来求。
结合直角坐标系问题,引入构造直角三角形的设想,形成解锐角三角比的基本思路,使学生能灵活应用锐角三角比求解。
有助于深入理解锐角三角比的概念,同时渗透了用坐标法定义三角比的思路。
四、
整
理
知
识
1、直角三角形中边与角的关系,四个锐角三角比。
2、怎样求一个角的锐角三角比。
3、直角三角形中三边的关系,三角的关系。
有助于学生在归纳过程中把所学的知识条理化、系统化。
五、
作
业
布
置
必做题:练习册25.1(2)
选做题:
如图:直线交轴于点A,交轴于点B,点D是线段AB的中点,如何求∠AOD的余弦值及正切值。
作业安排是为了让学生更进一步落实课堂教学目标,
选做题是为了满足不同层次学生的需求,为学有余力的学生提供发展空间.
教学设计说明:在直角三角形中,一个锐角的三角比有4个,正切和余切是上节课的内容,本节课主要讲正弦和余弦。本节课的重点是理解余弦、正弦的概念;熟练运用锐角三角比的概念进行有关计算。学好本节课,为今后学习解直角三角形打下重要基础。
本节课我通过复习,旨在让学生用类比的方法发现这样一个事实:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边(邻边)与斜边的比是一个固定值。并引导学生用上一节课的证明方法证明这个事实。然后与学生一起归纳得出正弦与余弦的定义。在接下来的应用环节上,例1:在巩固正弦余弦概念的基础上,让学生通过观察,论证得出正弦和余弦值的范围。例1的变式:在例1的基础上,添了一条高,求稍微复杂一点的图形中的锐角三角比,让学生知道除了直接在直角三角形中求三角比以外,还可以间接的求,把角转化成相同的角,进一步让学生体会到角度不变,锐角三角比是不变的。例2:主要是要让学生构造直角三角形,让学生明确求锐角三角比的前提条件是在直角三角形中。例2的变式更进一步强化锐角三角比概念同时跟函数结合起来。最后通过师生共同小结,发挥学生的主体作用,有利于学生巩固所学知识,培养学生归纳、概括的能力.作业安排是为了让学生更进一步落实课堂教学目标,而选做题则满足了不同层次学生的需求,为学有余力的学生提供发展空间。
整堂课的设计力求以问题思维为主线,让学生充分参与数学学习,获得广泛的数学经验,这样的设计是希望这节课能融基础性、灵活性、实践性于一体。我认为这样既注重知识的发生、发展、形成的过程,展现了对解题思路、解题方法、解题规律的探索概括,又能使学习者积极主动地将知识融入已构建的结构,而不是被动的接受并积累知识,从而“构建自己的知识体系”。并通过探索过程,不断丰富学生解决问题的策略,提高解决问题的能力,发展数学思维。
2
教学目标:
类比正切、余切概念的形成过程得到一个锐角的正弦与余弦的定义以及锐角三角比的定义。能熟练运用锐角三角比的概念进行有关计算。掌握直角三角形锐角三角比及其值的取值范围;在学习过程中培养学生分析问题解决问题的能力及学习数学的兴趣。
教学重点:理解余弦、正弦的概念;熟练运用锐角三角比的概念进行有关计算。
教学难点:灵活应用锐角三角比解决问题
教学过程:
教学环节
教学过程
设计意图
一、
回
顾
旧
知
上节课我们学了在直角三角形中一个锐角的对边与邻边之间的关系。
1.∠A的正切:tanA=
2.∠A的余切:cotA=
思考:我们是怎么说明一个锐角的对边与邻边的比值是一个定值的?
巩固正切、余切概念,并回忆上节课内容的证法,为本节课做铺垫。
二、
探
索
新
知
1、讨论:
在直角三角形中,当锐角A确定时,邻边与对边的比值随之确定外,还有其他两边之间的比值是确定的吗?
请学生用学过的知识说明。
先小组讨论,然后交流。
2、归纳:
(1)、∠A的对边和斜边的比值是确定的。
(2)、∠A的邻边和斜边的比值是确定的。
3、引出概念
(1)在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正弦.记作sinA.
sinA=
(2)在Rt△ABC中,∠C=90°,我们把锐角A的邻边与对边的比叫做∠A的余弦.记作cosA.
cosA=;
(3)一个锐角的正切、余切、正弦、余弦统称为这个锐角三角比。
借助于上节课的知识发挥学生的主观能动性,探讨正弦、余弦的概念,并培养学生团结协作的精神。
三、
应
用
新
知
例题1、如图:在Rt△ABC中,∠C=90°,AB=17,BC=8,求sinA、cosA、sinB和cosB的值。
思考:(1)在Rt△ABC中,∠C=90°,则cosB与sinA有什么关系?(cosB=
sinA=)
(互余的两个角,一个角的正弦与另一个角的余弦相等。)
(2)任何一个锐角的三角比的值都是正实数,其中正弦和余弦的值小于1,为什么?(0﹤sinA﹤1,0﹤cosA﹤1)
(3)在直角三角形中,如何求一个锐角的三角比?
变式:在例1的条件下,作CD⊥AB,垂足为点D,求∠BCD的正切、余切、正弦和余弦的值。
归纳:(1)求一个锐角的三角比,必须在直角三角形中。
(2)求一个锐角的三角比,可以用直接法或间接法,直接找锐角所在的直角三角形,或利用相等的角的转化在其他三角形里求。
例题2、如图,在直角坐标平面中有一点P(3,4).求OP与x轴正半轴的夹角的正切、余切、正弦、和余弦的值。
归纳:解这个题目的关键是构造直角三角形。
变式:当点P是正比例函数在第一象限的一个点,你能求出OP与x轴正半轴的夹角的正切、余切、正弦、和余弦的值吗?
巩固正弦余弦概念,会用已知边来求正弦余弦。
通过观察由学生自己总结出锐角三角比的值中正弦和余弦的值的范围,养成良好的学习习惯。
在比较复杂的图形中,让学生会求一个锐角的三角比。让学生知道求一个锐角的三角比可以把一个锐角转化成相同的角来求。
结合直角坐标系问题,引入构造直角三角形的设想,形成解锐角三角比的基本思路,使学生能灵活应用锐角三角比求解。
有助于深入理解锐角三角比的概念,同时渗透了用坐标法定义三角比的思路。
四、
整
理
知
识
1、直角三角形中边与角的关系,四个锐角三角比。
2、怎样求一个角的锐角三角比。
3、直角三角形中三边的关系,三角的关系。
有助于学生在归纳过程中把所学的知识条理化、系统化。
五、
作
业
布
置
必做题:练习册25.1(2)
选做题:
如图:直线交轴于点A,交轴于点B,点D是线段AB的中点,如何求∠AOD的余弦值及正切值。
作业安排是为了让学生更进一步落实课堂教学目标,
选做题是为了满足不同层次学生的需求,为学有余力的学生提供发展空间.
教学设计说明:在直角三角形中,一个锐角的三角比有4个,正切和余切是上节课的内容,本节课主要讲正弦和余弦。本节课的重点是理解余弦、正弦的概念;熟练运用锐角三角比的概念进行有关计算。学好本节课,为今后学习解直角三角形打下重要基础。
本节课我通过复习,旨在让学生用类比的方法发现这样一个事实:在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边(邻边)与斜边的比是一个固定值。并引导学生用上一节课的证明方法证明这个事实。然后与学生一起归纳得出正弦与余弦的定义。在接下来的应用环节上,例1:在巩固正弦余弦概念的基础上,让学生通过观察,论证得出正弦和余弦值的范围。例1的变式:在例1的基础上,添了一条高,求稍微复杂一点的图形中的锐角三角比,让学生知道除了直接在直角三角形中求三角比以外,还可以间接的求,把角转化成相同的角,进一步让学生体会到角度不变,锐角三角比是不变的。例2:主要是要让学生构造直角三角形,让学生明确求锐角三角比的前提条件是在直角三角形中。例2的变式更进一步强化锐角三角比概念同时跟函数结合起来。最后通过师生共同小结,发挥学生的主体作用,有利于学生巩固所学知识,培养学生归纳、概括的能力.作业安排是为了让学生更进一步落实课堂教学目标,而选做题则满足了不同层次学生的需求,为学有余力的学生提供发展空间。
整堂课的设计力求以问题思维为主线,让学生充分参与数学学习,获得广泛的数学经验,这样的设计是希望这节课能融基础性、灵活性、实践性于一体。我认为这样既注重知识的发生、发展、形成的过程,展现了对解题思路、解题方法、解题规律的探索概括,又能使学习者积极主动地将知识融入已构建的结构,而不是被动的接受并积累知识,从而“构建自己的知识体系”。并通过探索过程,不断丰富学生解决问题的策略,提高解决问题的能力,发展数学思维。
2
