沪教版(上海)初中数学九年级第一学期 26.3 二次函数y=a(x+m)2的图像 教案
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 26.3 二次函数y=a(x+m)2的图像 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 157.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-31 00:00:00 | ||
图片预览

文档简介
26.2(3)
二次函数的图像
教学目标
1.掌握二次函数的图像及基本性质;
2.经历二次函数与的图像的位置关系的探究,能由m的值确定图像平移的方向和距离;
3.在运用图形运动、变换的思想研究二次函数的过程中,通过独立思考,初步学会归纳、概括、提炼数学知识的方法.
教学重点
二次函数的图像及性质.
教学难点
在运用图形运动、变换的思想研究二次函数的过程中,探索二次函数的性质.
教学流程
教学过程
一、复习引入
1.说出下列二次函数的开口方向、对称轴和顶点坐标
(1)
;
(2).
2.将抛物线向
平移
个单位可以得到抛物线;将抛物线向
平移
个单位可以得到抛物线;将抛物线向
平移
个单位可以得到抛物线.
二、探究新知
探究1二次函数图像可以通过二次函数的图像平移得到吗?
…
-4
-3
-2
-1
0
1
2
3
…
…
…
-2
0
-2
…
…
-2
0
-2
…
…
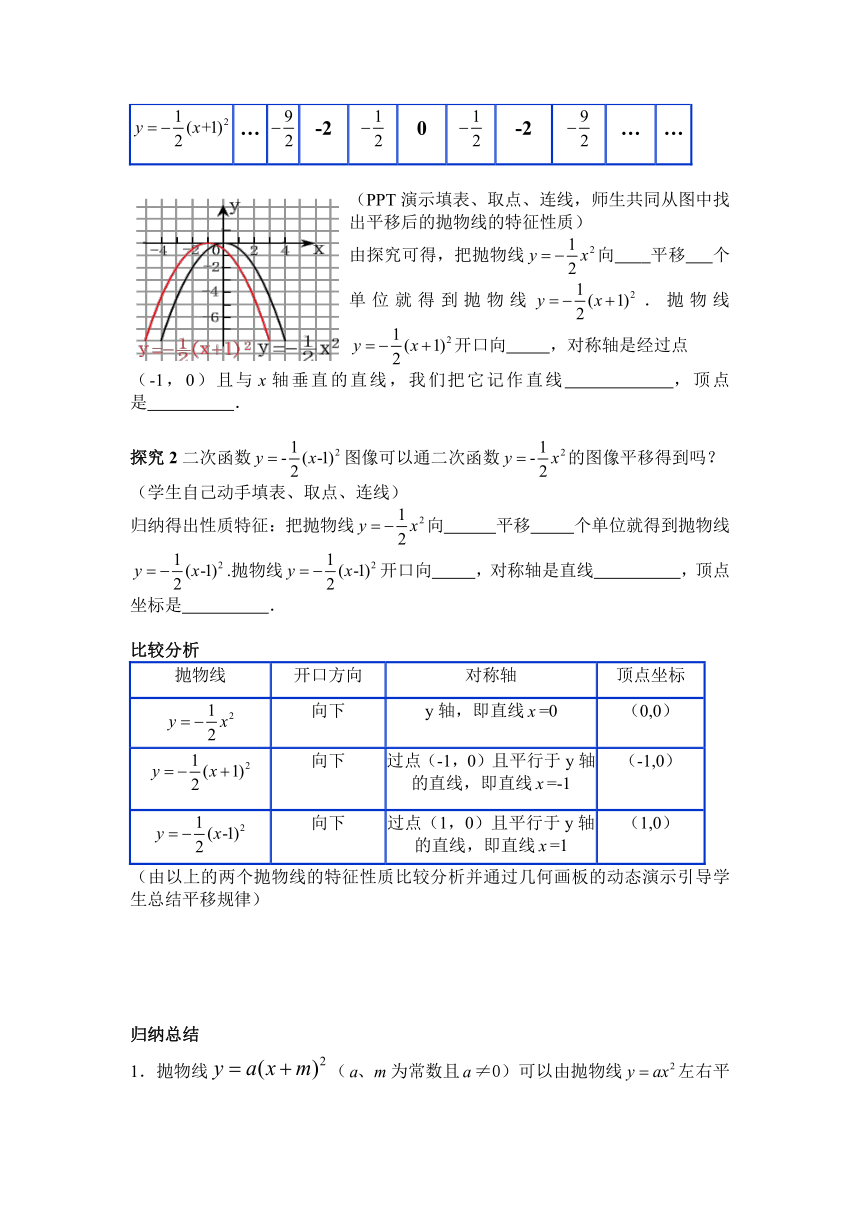
(PPT演示填表、取点、连线,师生共同从图中找出平移后的抛物线的特征性质)
由探究可得,把抛物线向
平移
个单位就得到抛物线.抛物线开口向
,对称轴是经过点
(-1,0)且与轴垂直的直线,我们把它记作直线
,顶点是
.
探究2二次函数图像可以通二次函数的图像平移得到吗?
(学生自己动手填表、取点、连线)
归纳得出性质特征:把抛物线向
平移
个单位就得到抛物线.抛物线开口向
,对称轴是直线
,顶点坐标是
.
比较分析
抛物线
开口方向
对称轴
顶点坐标
向下
y轴,即直线=0
(0,0)
向下
过点(-1,0)且平行于y轴的直线,即直线=-1
(-1,0)
向下
过点(1,0)且平行于y轴的直线,即直线=1
(1,0)
(由以上的两个抛物线的特征性质比较分析并通过几何画板的动态演示引导学生总结平移规律)
归纳总结
1.抛物线(为常数且≠0)可以由抛物线左右平移个单位得到.
>0,向左平移;<0,向右平移.
注意:左加右减
2.抛物线图像的性质特征:
(1)开口方向:>0,开口向上,顶点是它的最低点;
<0,开口向下,顶点是它的最高点.
(2)对称轴:过点(,0)且平行(重合)于轴的直线,即直线.
(3)顶点坐标:(,0)
三、巩固新知
1.二次函数的图像是
,它的开口向
,对称轴是
,顶点坐标
.
2.抛物线是由抛物线向
平移
个单位得到的,它的开口向
,对称轴是
,顶点坐标
.
3.将抛物线向左平移4个单位可得抛物线
,所得抛物线的对称轴是
;顶点坐标是
,顶点是它的最
点.
4.将抛物线向下平移2个单位后可得抛物线
,再向
平移
个单位可得抛物线.
5.将抛物线向
平移
个单位可得抛物线.
6.抛物线经过点(3,1),抛物线的对称轴是
,
解析式为
.
7.已知抛物线的图像对称轴是直线且经过点(0,5),
求a、m的值.
四、课堂小结
拓展提高
1.将抛物线沿着x轴翻折,所得的新抛物线
;将抛物线沿着y轴翻折,所得的新抛物线
;
将抛物线绕着它的顶点旋转180°,所得的新抛物线
.
2.将抛物线向左平移5个单位后得到抛物线的图象,若抛物线的顶点M,抛物线的顶点是N,
且与y轴交于点A.
求a、m的值;
(2)求
的面积.
五、布置作业
练习册P54-55
26.2(3)
教学设计说明
在本节课之前,学生已经学习了二次函数的概念和二次函数和的图像和性质。因此,本课的教学是在学习过的二次函数的基础上,运用类比探究的方法得出二次函数由平移得到的一般规律,由特殊到一般,总结得到二次函数的图像性质,并为下一节作铺垫。这样符合学生的认知规律,学生也能进一步体会数形结合的方法。
在教学过程中,由上一节上下平移的习题引出探究1,通过PPT演示填表、取点、连线,师生共同探讨的图像性质;再通过学生自己动手填表、取点、连线作出函数图像,体现学生是主体的教学地位,学生通过观察、分析、探究出函数的图像性质;再由特殊到一般,通过几何画板动态演示引导学生归纳出平移的一般规律,总结得出的图像性质。为了巩固新知,设计了一系列基础题供学生训练,对于学有余力的学生,我还设计了2个拓展提高训练。
二次函数的图像
教学目标
1.掌握二次函数的图像及基本性质;
2.经历二次函数与的图像的位置关系的探究,能由m的值确定图像平移的方向和距离;
3.在运用图形运动、变换的思想研究二次函数的过程中,通过独立思考,初步学会归纳、概括、提炼数学知识的方法.
教学重点
二次函数的图像及性质.
教学难点
在运用图形运动、变换的思想研究二次函数的过程中,探索二次函数的性质.
教学流程
教学过程
一、复习引入
1.说出下列二次函数的开口方向、对称轴和顶点坐标
(1)
;
(2).
2.将抛物线向
平移
个单位可以得到抛物线;将抛物线向
平移
个单位可以得到抛物线;将抛物线向
平移
个单位可以得到抛物线.
二、探究新知
探究1二次函数图像可以通过二次函数的图像平移得到吗?
…
-4
-3
-2
-1
0
1
2
3
…
…
…
-2
0
-2
…
…
-2
0
-2
…
…
(PPT演示填表、取点、连线,师生共同从图中找出平移后的抛物线的特征性质)
由探究可得,把抛物线向
平移
个单位就得到抛物线.抛物线开口向
,对称轴是经过点
(-1,0)且与轴垂直的直线,我们把它记作直线
,顶点是
.
探究2二次函数图像可以通二次函数的图像平移得到吗?
(学生自己动手填表、取点、连线)
归纳得出性质特征:把抛物线向
平移
个单位就得到抛物线.抛物线开口向
,对称轴是直线
,顶点坐标是
.
比较分析
抛物线
开口方向
对称轴
顶点坐标
向下
y轴,即直线=0
(0,0)
向下
过点(-1,0)且平行于y轴的直线,即直线=-1
(-1,0)
向下
过点(1,0)且平行于y轴的直线,即直线=1
(1,0)
(由以上的两个抛物线的特征性质比较分析并通过几何画板的动态演示引导学生总结平移规律)
归纳总结
1.抛物线(为常数且≠0)可以由抛物线左右平移个单位得到.
>0,向左平移;<0,向右平移.
注意:左加右减
2.抛物线图像的性质特征:
(1)开口方向:>0,开口向上,顶点是它的最低点;
<0,开口向下,顶点是它的最高点.
(2)对称轴:过点(,0)且平行(重合)于轴的直线,即直线.
(3)顶点坐标:(,0)
三、巩固新知
1.二次函数的图像是
,它的开口向
,对称轴是
,顶点坐标
.
2.抛物线是由抛物线向
平移
个单位得到的,它的开口向
,对称轴是
,顶点坐标
.
3.将抛物线向左平移4个单位可得抛物线
,所得抛物线的对称轴是
;顶点坐标是
,顶点是它的最
点.
4.将抛物线向下平移2个单位后可得抛物线
,再向
平移
个单位可得抛物线.
5.将抛物线向
平移
个单位可得抛物线.
6.抛物线经过点(3,1),抛物线的对称轴是
,
解析式为
.
7.已知抛物线的图像对称轴是直线且经过点(0,5),
求a、m的值.
四、课堂小结
拓展提高
1.将抛物线沿着x轴翻折,所得的新抛物线
;将抛物线沿着y轴翻折,所得的新抛物线
;
将抛物线绕着它的顶点旋转180°,所得的新抛物线
.
2.将抛物线向左平移5个单位后得到抛物线的图象,若抛物线的顶点M,抛物线的顶点是N,
且与y轴交于点A.
求a、m的值;
(2)求
的面积.
五、布置作业
练习册P54-55
26.2(3)
教学设计说明
在本节课之前,学生已经学习了二次函数的概念和二次函数和的图像和性质。因此,本课的教学是在学习过的二次函数的基础上,运用类比探究的方法得出二次函数由平移得到的一般规律,由特殊到一般,总结得到二次函数的图像性质,并为下一节作铺垫。这样符合学生的认知规律,学生也能进一步体会数形结合的方法。
在教学过程中,由上一节上下平移的习题引出探究1,通过PPT演示填表、取点、连线,师生共同探讨的图像性质;再通过学生自己动手填表、取点、连线作出函数图像,体现学生是主体的教学地位,学生通过观察、分析、探究出函数的图像性质;再由特殊到一般,通过几何画板动态演示引导学生归纳出平移的一般规律,总结得出的图像性质。为了巩固新知,设计了一系列基础题供学生训练,对于学有余力的学生,我还设计了2个拓展提高训练。
