苏科版七年级数学下册 第七章 平面图形的认识(二) 单元检测试题(word版含解析)
文档属性
| 名称 | 苏科版七年级数学下册 第七章 平面图形的认识(二) 单元检测试题(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 149.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 00:00:00 | ||
图片预览

文档简介
第七章
平面图形的认识(二)
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
下列说法正确的是(
)
A.有一组邻边相等的四边形是菱形
B.四条边都相等的四边形是菱形
C.两条对角线相等的矩形是正方形
D.对角线相等的四边形是平行四边形
?
2.
如果是的中线,那么下列结论一定成立的有(
)
①;②;③.
A.个
B.个
C.个
D.个
?
3.
如图,正四边形有条对角线,正五边形有条对角线,正六边形有条对角线,则正十边形有(
)条对角线.
A.
B.
C.
D.
?
4.
若边形的内角和等于外角和的倍,则边数为?
?
?
?
A.
B.
C.
D.
?
5.
如图,在中,,沿图中虚线截去,则(?
?
?
?
)
A.
B.
C.
D.
?
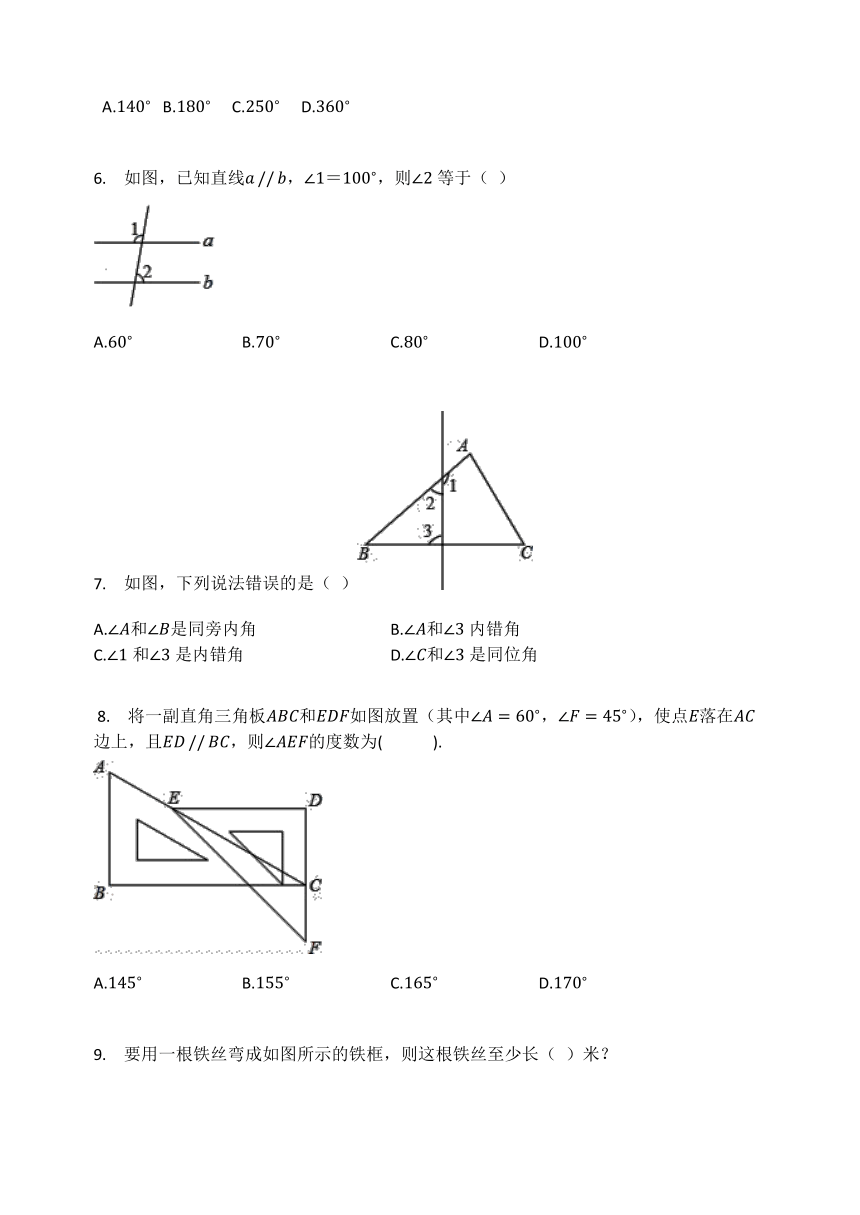
6.
如图,已知直线,=,则等于(
)
A.
B.
C.
D.
?
7.
如图,下列说法错误的是(
)
A.和是同旁内角
B.和内错角
C.和是内错角
D.和是同位角
?8.
将一副直角三角板和如图放置(其中,),使点落在边上,且,则的度数为(?
?
?
?
).
A.
B.
C.
D.
?
9.
要用一根铁丝弯成如图所示的铁框,则这根铁丝至少长(
)米?
A.
B.
C.
D.无法确定
?
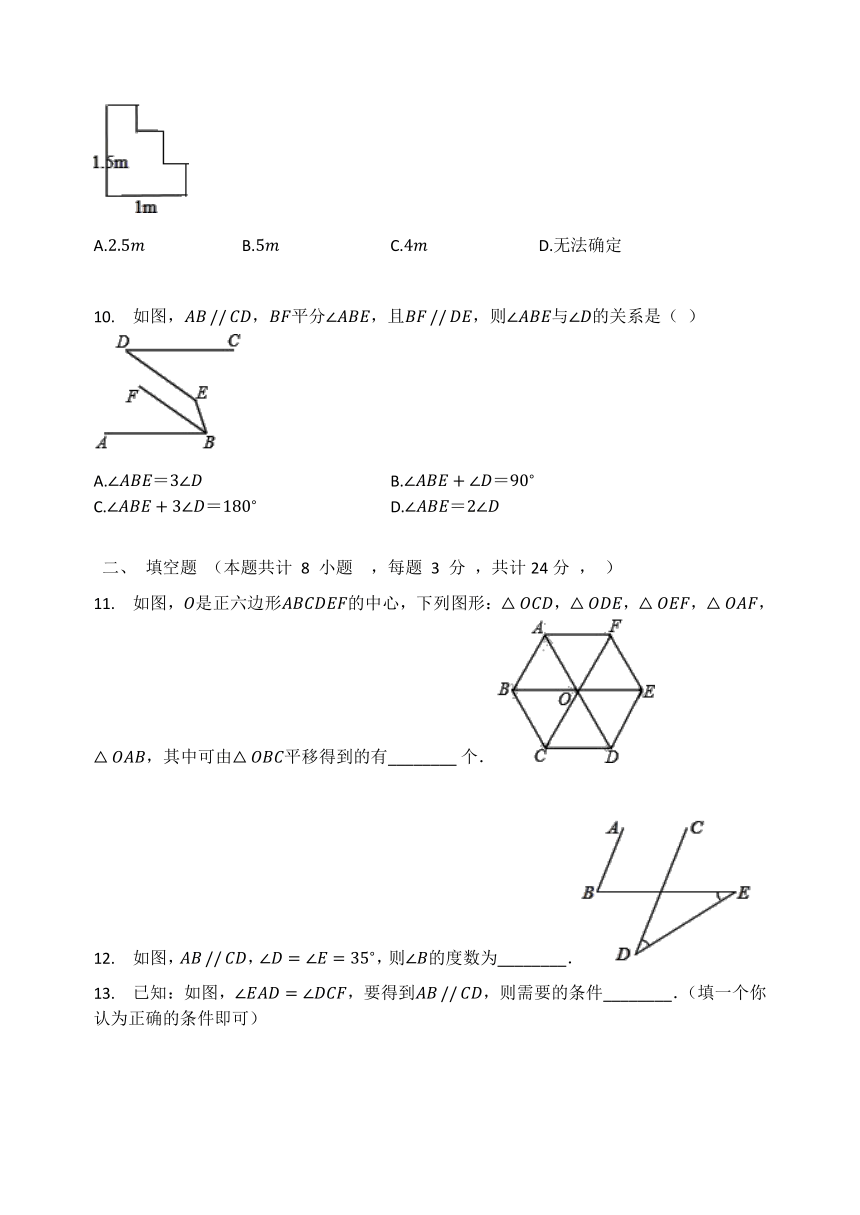
10.
如图,,平分,且,则与的关系是(
)
A.=
B.=
C.=
D.=
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
,
)
?
11.
如图,是正六边形的中心,下列图形:,,,,,其中可由平移得到的有________?个.
?
12.
如图,,,则的度数为________.
?
13.
已知:如图,,要得到,则需要的条件________.(填一个你认为正确的条件即可)
14.
已知四条线段的长分别为,,,,用其中的三条线段构成的三角形的周长是________.
?
15.
图中,有很多大大小小的三角形,这些三角形有的是单独显现的,有的是合并若干区块才得到的,这些位置不完全相同的三角形共有________个.
?
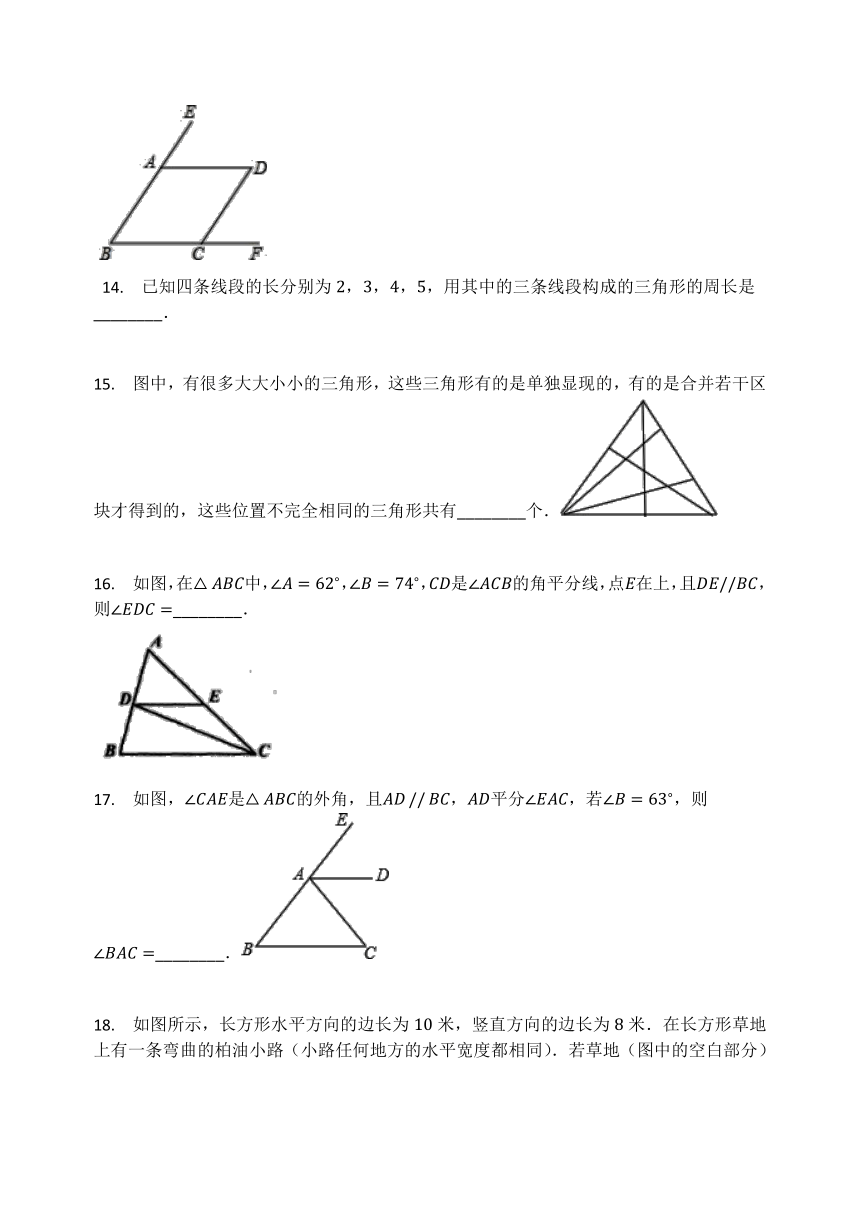
16.
如图,在中,,,是的角平分线,点在上,且,则________.
?
17.
如图,是的外角,且,平分,若,则________.
?
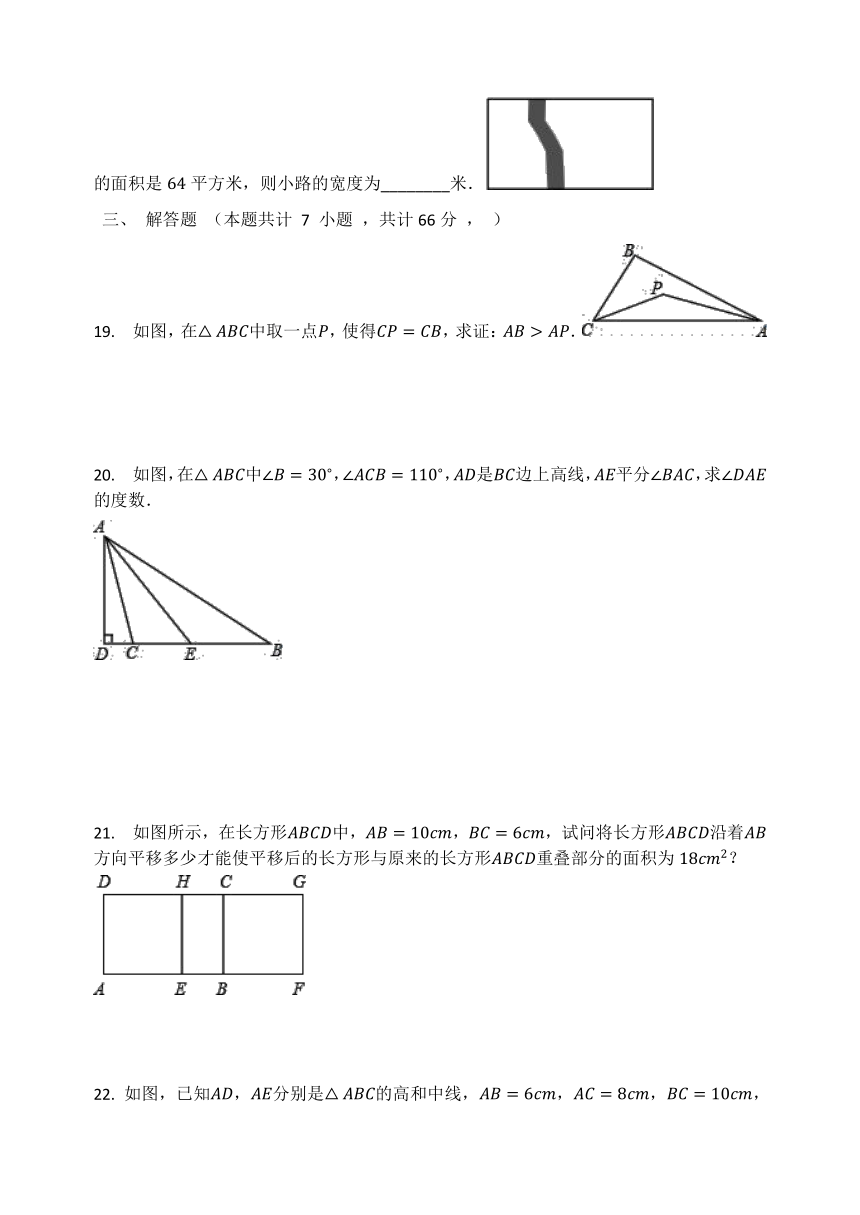
18.
如图所示,长方形水平方向的边长为米,竖直方向的边长为米.在长方形草地上有一条弯曲的柏油小路(小路任何地方的水平宽度都相同).若草地(图中的空白部分)的面积是平方米,则小路的宽度为________米.
三、
解答题
(本题共计
7
小题
,共计66分
,
)
?
19.
如图,在中取一点,使得,求证:.
?
20.
如图,在中,,是边上高线,平分,求的度数.
?
21.
如图所示,在长方形中,,,试问将长方形沿着方向平移多少才能使平移后的长方形与原来的长方形重叠部分的面积为?
?
22.
如图,已知,分别是的高和中线,,,,.试求:
的长;
的面积;
和的周长的差.
?
23.
如图,平分,平分,、交于,若,,求的度数.
?
24.
如图,中,,是的角平分线,,求的度数.
?
25.
一个零件的形状如图所示,按规定应等于,、应分别是和,李叔叔量得是多少时,才能断定这个零件是合格的,你能说出道理吗?
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:、有一组邻边相等的平行四边形是菱形,故此选项错误;
、四条边都相等的四边形是菱形,此选项正确;
、两条对角线相等的菱形是正方形,故此选项错误;
、对角线互相平分的四边形是平行四边形,故此选项错误;
故选:.
2.
【答案】
B
【解答】
解:∵
是的中线,
∴
,故①正确;
∵
与不一定互相垂直,
∴
与不一定相等,故②错误;
设中边上的高为,
则,故③正确.
故选:.
3.
【答案】
B
【解答】
解:当时,
,
即凸十边形的对角线有条.
故选.
4.
【答案】
C
【解答】
解:设这个多边形的边数为,则依题意可得:
,
解得.
故选.
5.
【答案】
C
【解答】
解:∵
,
∴
.
故选.
6.
【答案】
C
【解答】
∵
,=,
∴
=,
∴
=,
7.
【答案】
B
【解答】
解:、和是同旁内角,故本选项错误;
、和不是内错角,故本选项正确;
、和是内错角,故本选项错误;
、和是同位角,故本选项错误;
故选.
8.
【答案】
C
【解答】
解:∵
,,
∴
,
∵
,
∴
,
∴
,
.
故选.
9.
【答案】
B
【解答】
这根铁丝至少长:=,
10.
【答案】
D
【解答】
证明:如图,延长交的延长线于,
∵
,
∴
=,
∵
,
∴
=,
∴
=,
∵
平分,
∴
==,即=.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
【解答】
解:方向发生了变化,不是平移得到;
符合平移的性质,是平移得到;
方向发生了变化,不是平移得到;
符合平移的性质,是平移得到;
方向发生了变化,不是平移得到.
故答案为:.
12.
【答案】
【解答】
解:∵
,
∴
,
∵
,
∴
.
故答案为:.
13.
【答案】
【解答】
解:可以添加条件,理由如下:
∵
,,
∴
,
∴
.
故答案为:.
14.
【答案】
或或
【解答】
解:由这四条线段组成三角形的情况有:、、,
故周长为或或.
故答案为:或或.
15.
【答案】
【解答】
解:
以为边的三角形有:,,;
以为边的三角形有:,;
以为边的三角形有:,,,,,,;
以为边的三角形有:,,;
以为边的三角形有:;
以为边的三角形有:,,,
以为边的三角形有:,;
以为边的三角形有:
以为边的三角形有:,;
以为边的三角形有:,
以为边的三角形有:,
以为边的三角形有:,,
以为边的三角形有:,,
以为边的三角形有:,,
以为边的三角形有:
以为边的三角形有:
以为边的三角形有:
以为边的三角形有:;
三角形共有个.
故答案是:.
16.
【答案】
【解答】
此题暂无解答
17.
【答案】
【解答】
解:∵
,,
∴
,
∵
是的平分线,
∴
,
∴
,
故答案为:
18.
【答案】
【解答】
解:设小路的宽为米,根据题意得,
,
解得米.
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
证明:如图,
延长到交于,连结.
∵
在中,,
在中,,
∴
,
∵
,
∴
.
【解答】
证明:如图,
延长到交于,连结.
∵
在中,,
在中,,
∴
,
∵
,
∴
.
20.
【答案】
解:∵
,,
∴
,
∵
平分,
∴
,
∵
,是边上高线,
∴
,
∴
.
【解答】
解:∵
,,
∴
,
∵
平分,
∴
,
∵
,是边上高线,
∴
,
∴
.
21.
【答案】
解:设平移线段,到,到,则,
∵
,
∴
,
解得,
∴
向右平移.
【解答】
解:设平移线段,到,到,则,
∵
,
∴
,
解得,
∴
向右平移.
22.
【答案】
解:∵
,是边上的高,
∴
,
∴
,
即的长度为;
如图,∵
是直角三角形,
,,,
∴
.
又∵
是边的中线,
∴
,
∴
,即,
∴
.
∴
的面积是.
∵
为边上的中线,
∴
,
∴
的周长的周长
,
即和的周长的差是.
【解答】
解:∵
,是边上的高,
∴
,
∴
,
即的长度为;
如图,∵
是直角三角形,
,,,
∴
.
又∵
是边的中线,
∴
,
∴
,即,
∴
.
∴
的面积是.
∵
为边上的中线,
∴
,
∴
的周长的周长
,
即和的周长的差是.
23.
【答案】
解:如图,连接.
∵
是的平分线,是的平分线,
∴
,,
又,,
∴
,,
∴
,
∴
,
∴
,即,
∴
.
【解答】
解:如图,连接.
∵
是的平分线,是的平分线,
∴
,,
又,,
∴
,,
∴
,
∴
,
∴
,即,
∴
.
24.
【答案】
解:在中,
,,
∴
,
∵
是的角平分线,
∴
,
∵
,
∴
.
【解答】
解:在中,
,,
∴
,
∵
是的角平分线,
∴
,
∵
,
∴
.
25.
【答案】
解:延长交于,
.
【解答】
解:延长交于,
.
平面图形的认识(二)
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
下列说法正确的是(
)
A.有一组邻边相等的四边形是菱形
B.四条边都相等的四边形是菱形
C.两条对角线相等的矩形是正方形
D.对角线相等的四边形是平行四边形
?
2.
如果是的中线,那么下列结论一定成立的有(
)
①;②;③.
A.个
B.个
C.个
D.个
?
3.
如图,正四边形有条对角线,正五边形有条对角线,正六边形有条对角线,则正十边形有(
)条对角线.
A.
B.
C.
D.
?
4.
若边形的内角和等于外角和的倍,则边数为?
?
?
?
A.
B.
C.
D.
?
5.
如图,在中,,沿图中虚线截去,则(?
?
?
?
)
A.
B.
C.
D.
?
6.
如图,已知直线,=,则等于(
)
A.
B.
C.
D.
?
7.
如图,下列说法错误的是(
)
A.和是同旁内角
B.和内错角
C.和是内错角
D.和是同位角
?8.
将一副直角三角板和如图放置(其中,),使点落在边上,且,则的度数为(?
?
?
?
).
A.
B.
C.
D.
?
9.
要用一根铁丝弯成如图所示的铁框,则这根铁丝至少长(
)米?
A.
B.
C.
D.无法确定
?
10.
如图,,平分,且,则与的关系是(
)
A.=
B.=
C.=
D.=
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
,
)
?
11.
如图,是正六边形的中心,下列图形:,,,,,其中可由平移得到的有________?个.
?
12.
如图,,,则的度数为________.
?
13.
已知:如图,,要得到,则需要的条件________.(填一个你认为正确的条件即可)
14.
已知四条线段的长分别为,,,,用其中的三条线段构成的三角形的周长是________.
?
15.
图中,有很多大大小小的三角形,这些三角形有的是单独显现的,有的是合并若干区块才得到的,这些位置不完全相同的三角形共有________个.
?
16.
如图,在中,,,是的角平分线,点在上,且,则________.
?
17.
如图,是的外角,且,平分,若,则________.
?
18.
如图所示,长方形水平方向的边长为米,竖直方向的边长为米.在长方形草地上有一条弯曲的柏油小路(小路任何地方的水平宽度都相同).若草地(图中的空白部分)的面积是平方米,则小路的宽度为________米.
三、
解答题
(本题共计
7
小题
,共计66分
,
)
?
19.
如图,在中取一点,使得,求证:.
?
20.
如图,在中,,是边上高线,平分,求的度数.
?
21.
如图所示,在长方形中,,,试问将长方形沿着方向平移多少才能使平移后的长方形与原来的长方形重叠部分的面积为?
?
22.
如图,已知,分别是的高和中线,,,,.试求:
的长;
的面积;
和的周长的差.
?
23.
如图,平分,平分,、交于,若,,求的度数.
?
24.
如图,中,,是的角平分线,,求的度数.
?
25.
一个零件的形状如图所示,按规定应等于,、应分别是和,李叔叔量得是多少时,才能断定这个零件是合格的,你能说出道理吗?
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:、有一组邻边相等的平行四边形是菱形,故此选项错误;
、四条边都相等的四边形是菱形,此选项正确;
、两条对角线相等的菱形是正方形,故此选项错误;
、对角线互相平分的四边形是平行四边形,故此选项错误;
故选:.
2.
【答案】
B
【解答】
解:∵
是的中线,
∴
,故①正确;
∵
与不一定互相垂直,
∴
与不一定相等,故②错误;
设中边上的高为,
则,故③正确.
故选:.
3.
【答案】
B
【解答】
解:当时,
,
即凸十边形的对角线有条.
故选.
4.
【答案】
C
【解答】
解:设这个多边形的边数为,则依题意可得:
,
解得.
故选.
5.
【答案】
C
【解答】
解:∵
,
∴
.
故选.
6.
【答案】
C
【解答】
∵
,=,
∴
=,
∴
=,
7.
【答案】
B
【解答】
解:、和是同旁内角,故本选项错误;
、和不是内错角,故本选项正确;
、和是内错角,故本选项错误;
、和是同位角,故本选项错误;
故选.
8.
【答案】
C
【解答】
解:∵
,,
∴
,
∵
,
∴
,
∴
,
.
故选.
9.
【答案】
B
【解答】
这根铁丝至少长:=,
10.
【答案】
D
【解答】
证明:如图,延长交的延长线于,
∵
,
∴
=,
∵
,
∴
=,
∴
=,
∵
平分,
∴
==,即=.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
【解答】
解:方向发生了变化,不是平移得到;
符合平移的性质,是平移得到;
方向发生了变化,不是平移得到;
符合平移的性质,是平移得到;
方向发生了变化,不是平移得到.
故答案为:.
12.
【答案】
【解答】
解:∵
,
∴
,
∵
,
∴
.
故答案为:.
13.
【答案】
【解答】
解:可以添加条件,理由如下:
∵
,,
∴
,
∴
.
故答案为:.
14.
【答案】
或或
【解答】
解:由这四条线段组成三角形的情况有:、、,
故周长为或或.
故答案为:或或.
15.
【答案】
【解答】
解:
以为边的三角形有:,,;
以为边的三角形有:,;
以为边的三角形有:,,,,,,;
以为边的三角形有:,,;
以为边的三角形有:;
以为边的三角形有:,,,
以为边的三角形有:,;
以为边的三角形有:
以为边的三角形有:,;
以为边的三角形有:,
以为边的三角形有:,
以为边的三角形有:,,
以为边的三角形有:,,
以为边的三角形有:,,
以为边的三角形有:
以为边的三角形有:
以为边的三角形有:
以为边的三角形有:;
三角形共有个.
故答案是:.
16.
【答案】
【解答】
此题暂无解答
17.
【答案】
【解答】
解:∵
,,
∴
,
∵
是的平分线,
∴
,
∴
,
故答案为:
18.
【答案】
【解答】
解:设小路的宽为米,根据题意得,
,
解得米.
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
证明:如图,
延长到交于,连结.
∵
在中,,
在中,,
∴
,
∵
,
∴
.
【解答】
证明:如图,
延长到交于,连结.
∵
在中,,
在中,,
∴
,
∵
,
∴
.
20.
【答案】
解:∵
,,
∴
,
∵
平分,
∴
,
∵
,是边上高线,
∴
,
∴
.
【解答】
解:∵
,,
∴
,
∵
平分,
∴
,
∵
,是边上高线,
∴
,
∴
.
21.
【答案】
解:设平移线段,到,到,则,
∵
,
∴
,
解得,
∴
向右平移.
【解答】
解:设平移线段,到,到,则,
∵
,
∴
,
解得,
∴
向右平移.
22.
【答案】
解:∵
,是边上的高,
∴
,
∴
,
即的长度为;
如图,∵
是直角三角形,
,,,
∴
.
又∵
是边的中线,
∴
,
∴
,即,
∴
.
∴
的面积是.
∵
为边上的中线,
∴
,
∴
的周长的周长
,
即和的周长的差是.
【解答】
解:∵
,是边上的高,
∴
,
∴
,
即的长度为;
如图,∵
是直角三角形,
,,,
∴
.
又∵
是边的中线,
∴
,
∴
,即,
∴
.
∴
的面积是.
∵
为边上的中线,
∴
,
∴
的周长的周长
,
即和的周长的差是.
23.
【答案】
解:如图,连接.
∵
是的平分线,是的平分线,
∴
,,
又,,
∴
,,
∴
,
∴
,
∴
,即,
∴
.
【解答】
解:如图,连接.
∵
是的平分线,是的平分线,
∴
,,
又,,
∴
,,
∴
,
∴
,
∴
,即,
∴
.
24.
【答案】
解:在中,
,,
∴
,
∵
是的角平分线,
∴
,
∵
,
∴
.
【解答】
解:在中,
,,
∴
,
∵
是的角平分线,
∴
,
∵
,
∴
.
25.
【答案】
解:延长交于,
.
【解答】
解:延长交于,
.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
