人教版数学五上多边形整理与复习课件(82张)
文档属性
| 名称 | 人教版数学五上多边形整理与复习课件(82张) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 00:00:00 | ||
图片预览





文档简介
(共82张PPT)
多边形的面积
整理和复习
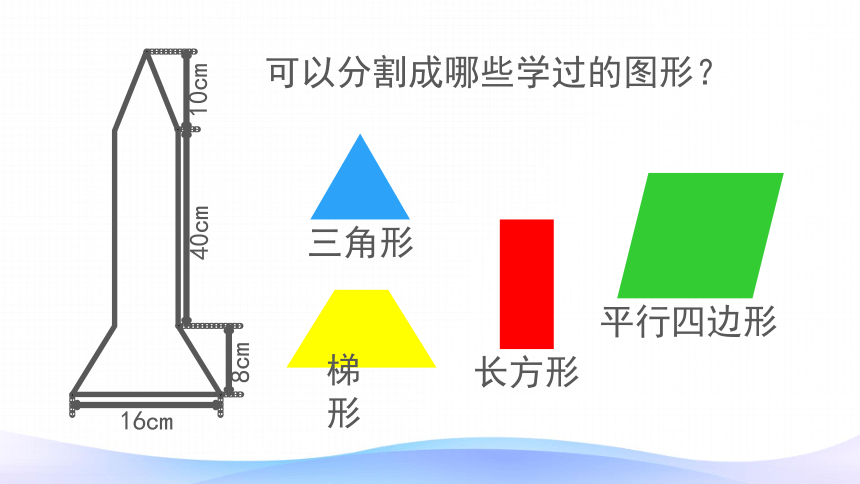
可以分割成哪些学过的图形?
三角形
长方形
梯形
平行四边形
10cm
40cm
8cm
16cm
三角形
长方形
梯形
平行四边形
多边形
整理和复习
三角形
长方形
梯形
平行四边形
写出这些多边形的公式
三角形
长方形
梯形
平行四边形
写出这些多边形的公式
S=ah÷2
S=ab
S=ah
S=(a+b)×h÷2
平行四边形
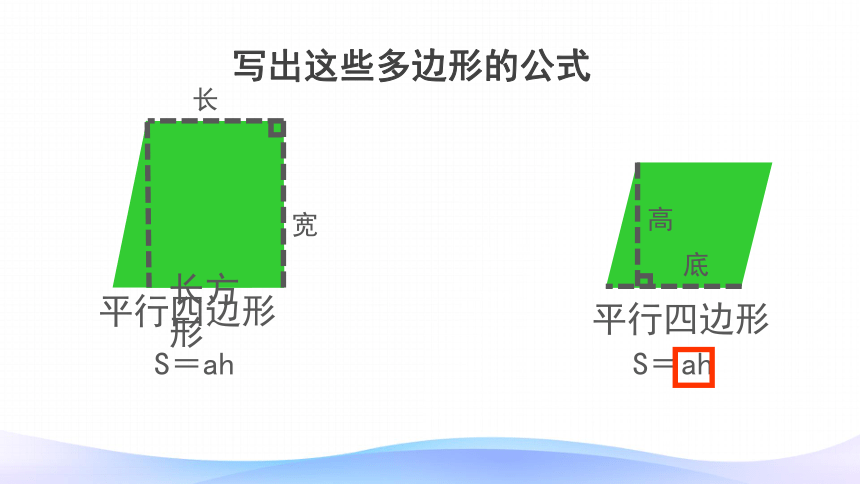
写出这些多边形的公式
平行四边形
长方形
长
底
宽
高
S=ah
S=ah
三角形
写出这些多边形的公式
S=ah÷2
三角形
平行四边形
底
底
高
高
S=ah÷2
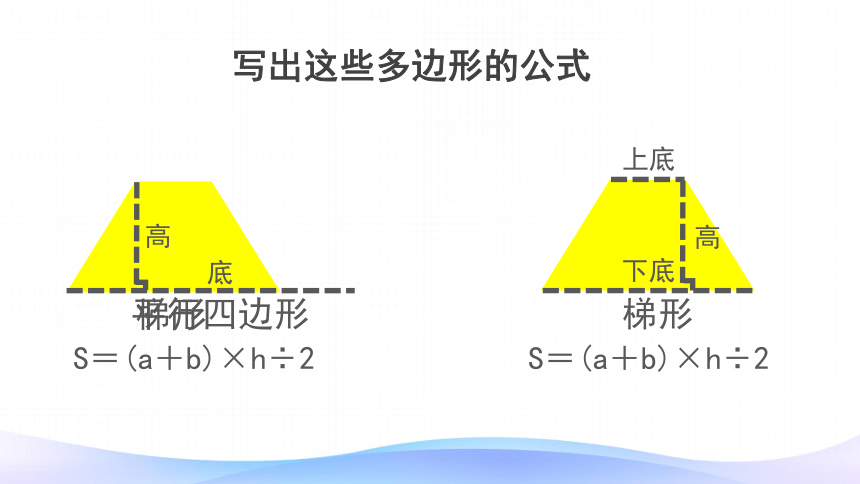
写出这些多边形的公式
梯形
S=(a+b)×h÷2
梯形
S=(a+b)×h÷2
底
高
高
上底
下底
平行四边形
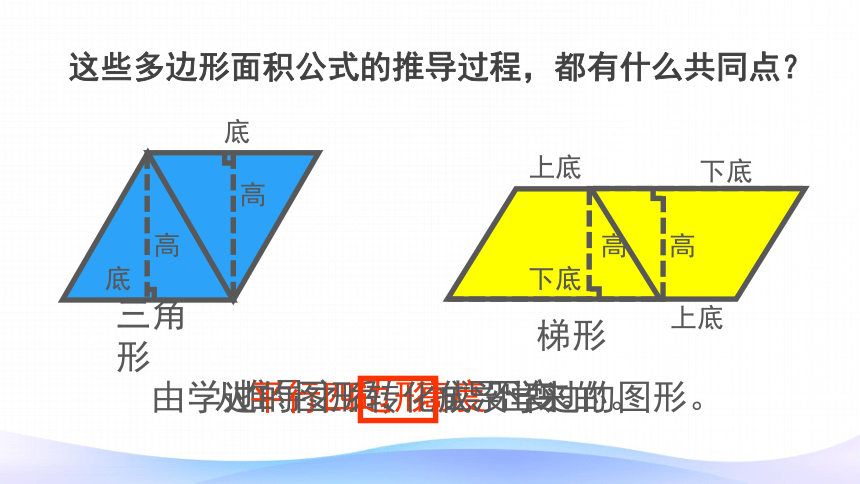
这些多边形面积公式的推导过程,都有什么共同点?
梯形
高
上底
下底
三角形
底
高
底
高
高
上底
下底
推导之后,高度不变。
从平行四边形推导出来的。
由学过的图形转化成没学过的图形。
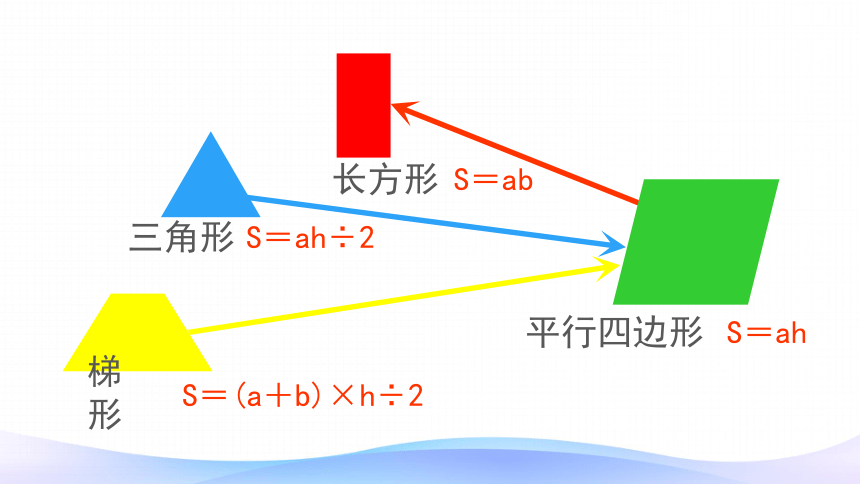
三角形
梯形
平行四边形
S=ah÷2
S=ab
S=ah
S=(a+b)×h÷2
长方形
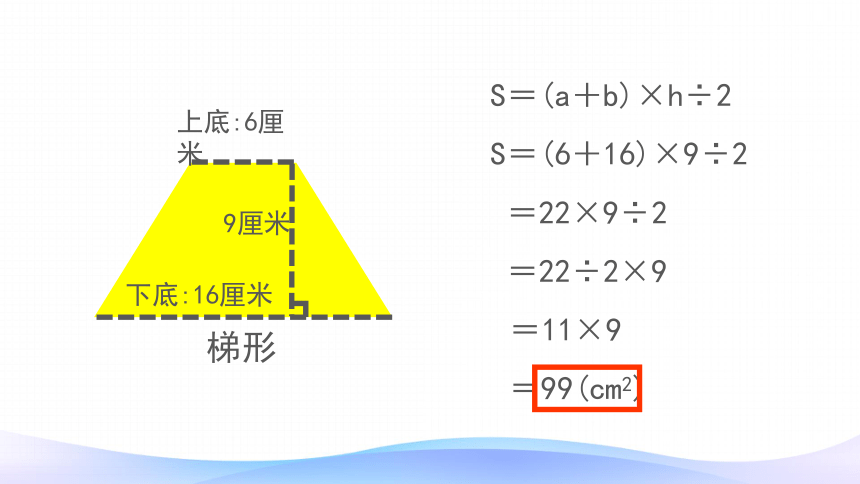
梯形
9厘米
上底:6厘米
下底:16厘米
S=(a+b)×h÷2
S=(6+16)×9÷2
=22×9÷2
=22÷2×9
=99(cm2)
=11×9
梯形
梯形与哪些图形的形状比较接近?
三角形
平行四边形
梯形怎么变成三角形?又怎么变成平行四边形?
梯形
梯形
梯形怎么变成三角形?
三角形
把梯形的上底变成底就是一个三角形。
上底
底
梯形
梯形怎么变成平行四边形?
平行四边形
把梯形的上底变为和下底相等,可以变为一个平行四边形。
梯形
将梯形变成三角形。
三角形
计算三角形的面积。
9厘米
16厘米
S=(a+b)×h÷2
计算三角形的面积。
三角形
S=(a+b)h÷2
S=(16+0)×9÷2
=16÷2×9
=8×9
=72(cm2)
9厘米
16厘米
=16×9÷2
S=ah÷2
S=16×9÷2
=16÷2×9
=8×9
=72(cm2)
梯形
将梯形变成平行四边形。
平行四边形
16厘米
计算平行四边形的面积。
平行四边形
16厘米
9厘米
计算平行四边形的面积。
16厘米
S=(a+b)h÷2
S=(16+16)×9÷2
=32÷2×9
=16×9
=144(cm2)
=32×9÷2
平行四边形
9厘米
S=ah
S=16×9
=144(cm2)
问:对比两种计算方式,你有什么想说的?
三角形
S=(a+b)h÷2
S=(16+0)×9÷2
=16÷2×9
=8×9
=72(cm2)
9厘米
16厘米
=16×9÷2
S=ah÷2
S=16×9÷2
=16÷2×9
=8×9
=72(cm2)
16厘米
S=(a+b)h÷2
S=(16+16)×9÷2
=32÷2×9
=16×9
=144(cm2)
=32×9÷2
平行四边形
9厘米
S=ah
S=16×9
=144(cm2)
问:对比两种计算方式,你有什么想说的?
答:梯形的面积公式既可以计算平行四边形的,也可以计算三角形的面积。
S=(a+b)h÷2
问:梯形的面积公式还可以计算哪些多边形的面积?
答:可以计算长方形和正方形的面积。
答:正方形是长方形推导出来的,长方形是平行四边形推导出来的,他们三个之间有联系。
问:为什么梯形的面积公式可以计算长方形和正方形的面积?
答:两个梯形可以变成平行四边形,平行四边形面积是由长方形推导出来的,长方形是由正方形转化的,正方形就是特殊的长方形。
问:为什么梯形的面积公式可以计算长方形和正方形的面积?
三角形
长方形
梯形
平行四边形
S=ah÷2
S=ab
S=ah
S=(a+b)×h÷2
三角形
长方形
梯形
平行四边形
S=ah÷2
S=ab
S=ah
S=(a+b)×h÷2
要想利用这些面积公式来计算它们的面积,必须要知道哪两个条件?
需要知道这些图形的底和高。
平行四边形
平行四边形
高度相等
观察这两个平行四边形,你有什么发现?
等底等高
观察这两个平行四边形,你有什么发现?
平行四边形的底相等,高也相等。
等底等高
平行四边形
平行四边形
等底等高
观察这两个平行四边形,你有什么发现?
面积相等
形状不同
三角形
三角形
等底等高
观察这两个三角形,你有什么发现?
观察这两个三角形,你有什么发现?
两个三角形的底相等,高也相等。
三角形
三角形
观察这两个三角形,你有什么发现?
等底等高
面积相等
形状不同
总结你的发现
三角形
三角形
平行四边形
平行四边形
等底等高的两个三角形或者平行四边形,它们的面积相等,但是形状不一定相同。
等底等高的两个三角形或者平行四边形,它们的面积相等,但是形状不一定相同。
总结你的发现
长方形
平行四边形
长方形与平行四边形,它们有什么关系?
宽
底
长
高
等底等高
面积相等
6厘米
12厘米
72平方厘米
长方形
平行四边形
宽
底
长
高
6厘米
12厘米
72平方厘米
等底等高的图形,面积是不会变的。
长方形与平行四边形,它们有什么关系?
等底等高
一样大
仔细观察,两个蓝色的面积哪个大?
一样大
仔细观察,两个蓝色的面积哪个大?
相等
仔细观察,两个蓝色的面积哪个大?
这两个三角形一直都是等底等高的。
相等
去掉公共的部分,剩下的蓝色部分面积怎么样?
相等
去掉公共的部分,剩下的蓝色部分面积怎么样?
等底等高的两个多边形面积相等。
周长没变。
如果多边形的面积增大或者减少,又与它们的底和高,有什么关系呢?
长:14.4厘米
宽:7.7厘米
高变小,底没变。
周长没变。
如果多边形的面积增大或者减少,又与它们的底和高,有什么关系呢?
长:14.4厘米
宽:7.7厘米
高变长,面积也变大。
底没变,高变长,面积变大。
底没变,高变长,面积变大。
高变短,底没变,面积缩小。
三角形底不变时,高变长或者是变短,它的面积也会随之变大或者是减小。
底不变时,面积随着高的变化而变化。
高没变,底变长,面积变大。
高不变时,面积随着底的变化而变化。
高没变,底变短,面积随之变小。
它们的底和高都是正方形的边长。
A
B
C
D
E
F
三角形ABC和三角形DEF,哪个面积大?
它们的面积一样大。
它们是等底等高的。
A
B
C
D
E
F
三角形ABC和三角形DEF,哪个面积大?
面积相同。
A
B
C
三角形ABC和三角形DEF,哪个面积大?
E
F
D
三角形DEF的面积变大了。
面积比之前大一倍。
因为它的底从一个小格挪到了第二个小格,它的底扩大到了原来的底的两倍。
三角形
长方形
梯形
平行四边形
S=ah÷2
S=ab
S=ah
S=(a+b)×h÷2
这些圆木,一共有多少根?
用数一数的办法,数出来这些原木有多少根。
可以用数层数的方法,先数出原木的上层是6根,再数出它的层数是4层,然后用四层乘6,等于24根。
这些圆木,一共有多少根?
每层的根数
×层数
每层的根数与层数,和这个长方形,有什么关系?
长方形
圆木的层数就是长方形的长和宽。
长:6
宽:4
这个长方形的面积,是多少?
长方形
6×4=24
长:6
宽:4
长方形的面积与长方形算出来的根数,有什么关系?
长:6
宽:4
相等
横截面是长方形的圆木,可以用长方形的面积公式,去算它们的面积。
这些圆木,一共有多少根?
这些圆木,一共有多少根?
(2+6)×5÷2
=8×5÷2
=40÷2
=20
2表示圆木顶层的根数,
6表示圆木的底层的根数,
5表示圆木的层数。
这些圆木,一共有多少根?
5
2
6
20根
这些圆木,一共有多少根?
20根
(2+6)×5÷2
=8×5÷2
=40÷2
=20
这些圆木,一共有多少根?
这些圆木,一共有多少根?
(1+6)×6÷2
=7×6÷2
=42÷2
=21
S=ah÷2
=6×6÷2
=36÷2
=18
21根
上底为0的时候,可以把它看成三角形。
这些圆木,一共有多少根?
21根
6
1
6
计算像这样的圆木堆它的方法。
21根
6
1
6
用它的顶层根数再加上它的底层根数,再乘层数,再除以2。
计算像这样的圆木堆它的方法。
21根
6
1
6
梯形的面积公式
总根数=(顶层根数+底层根数)×层数÷2
利用梯形的面积公式,还可以计算什么?
梯形的面积公式
总根数=(顶层根数+底层根数)×层数÷2
用梯形的面积公式,还可以计算火箭。
观察一下,每一层的根数,你有什么发现?
21根
6
1
6
连续的自然数字
前一层的根数比上一层的根数少1。
利用梯形的面积公式,还可以计算什么?
梯形的面积公式
总根数=(顶层根数+底层根数)×层数÷2
梯形的面积公式,除了可以计算圆木堆的总根数,还可以计算,连续算数的和。
三角形没有底,长方形没有宽,梯形没有上底。
都是一样长,都是8厘米。
10cm
40cm
8cm
16cm
8cm
8cm
可以分割的图形:___________________
三角形、长方形、梯形
组合图形的面积:__________________
可以分割的图形:___________________
10cm
40cm
8cm
16cm
三角形、长方形、梯形
S=ah÷2
=10×8÷2
=10×4
=40(cm2)
8cm
8cm
组合图形的面积:__________________
S=ah
=40×8
=320(cm2)
S=(a+b)h÷2
=(16+8)×8÷2
=24×8÷2
=96(cm2)
40+320+96
=456(cm2)
两个直角三角形的面积加起来,就是正方形的面积。
计算阴影部分的面积
5cm
4cm
S=(ah÷2)+(ah÷2)
=(5×4÷2)+(4×4÷2)
=10+8
=18(cm2)
计算阴影部分的面积
它的上底是4厘米,下底是5厘米,高是5厘米。
S=(a+b)h÷2
=(4+5)×4÷2
=9×4÷2
=9×2
=18(cm2)
5cm
4cm
计算阴影部分的面积
把这个图形看成一个平行四边形。
20(cm2)
它的上底是4厘米,下底是5厘米,不相等。
5cm
4cm
梯形的面积公式,可以帮我们解决圆木的问题;
课堂小结
梯形的面积,既可以推断平行四边形的面积,还可以推断三角形的面积;
梯形的面积公式,可以计算连续的层数;
等底等高的三角形和平行四边形,它们的面积相同,但是形状不一定一样;
课堂小结
计算阴影部分的面积;
可以把阴影部分,分成两个三角形来计算,也可以把阴影部分,看成一个梯形来计算。
再见!
多边形的面积
整理和复习
可以分割成哪些学过的图形?
三角形
长方形
梯形
平行四边形
10cm
40cm
8cm
16cm
三角形
长方形
梯形
平行四边形
多边形
整理和复习
三角形
长方形
梯形
平行四边形
写出这些多边形的公式
三角形
长方形
梯形
平行四边形
写出这些多边形的公式
S=ah÷2
S=ab
S=ah
S=(a+b)×h÷2
平行四边形
写出这些多边形的公式
平行四边形
长方形
长
底
宽
高
S=ah
S=ah
三角形
写出这些多边形的公式
S=ah÷2
三角形
平行四边形
底
底
高
高
S=ah÷2
写出这些多边形的公式
梯形
S=(a+b)×h÷2
梯形
S=(a+b)×h÷2
底
高
高
上底
下底
平行四边形
这些多边形面积公式的推导过程,都有什么共同点?
梯形
高
上底
下底
三角形
底
高
底
高
高
上底
下底
推导之后,高度不变。
从平行四边形推导出来的。
由学过的图形转化成没学过的图形。
三角形
梯形
平行四边形
S=ah÷2
S=ab
S=ah
S=(a+b)×h÷2
长方形
梯形
9厘米
上底:6厘米
下底:16厘米
S=(a+b)×h÷2
S=(6+16)×9÷2
=22×9÷2
=22÷2×9
=99(cm2)
=11×9
梯形
梯形与哪些图形的形状比较接近?
三角形
平行四边形
梯形怎么变成三角形?又怎么变成平行四边形?
梯形
梯形
梯形怎么变成三角形?
三角形
把梯形的上底变成底就是一个三角形。
上底
底
梯形
梯形怎么变成平行四边形?
平行四边形
把梯形的上底变为和下底相等,可以变为一个平行四边形。
梯形
将梯形变成三角形。
三角形
计算三角形的面积。
9厘米
16厘米
S=(a+b)×h÷2
计算三角形的面积。
三角形
S=(a+b)h÷2
S=(16+0)×9÷2
=16÷2×9
=8×9
=72(cm2)
9厘米
16厘米
=16×9÷2
S=ah÷2
S=16×9÷2
=16÷2×9
=8×9
=72(cm2)
梯形
将梯形变成平行四边形。
平行四边形
16厘米
计算平行四边形的面积。
平行四边形
16厘米
9厘米
计算平行四边形的面积。
16厘米
S=(a+b)h÷2
S=(16+16)×9÷2
=32÷2×9
=16×9
=144(cm2)
=32×9÷2
平行四边形
9厘米
S=ah
S=16×9
=144(cm2)
问:对比两种计算方式,你有什么想说的?
三角形
S=(a+b)h÷2
S=(16+0)×9÷2
=16÷2×9
=8×9
=72(cm2)
9厘米
16厘米
=16×9÷2
S=ah÷2
S=16×9÷2
=16÷2×9
=8×9
=72(cm2)
16厘米
S=(a+b)h÷2
S=(16+16)×9÷2
=32÷2×9
=16×9
=144(cm2)
=32×9÷2
平行四边形
9厘米
S=ah
S=16×9
=144(cm2)
问:对比两种计算方式,你有什么想说的?
答:梯形的面积公式既可以计算平行四边形的,也可以计算三角形的面积。
S=(a+b)h÷2
问:梯形的面积公式还可以计算哪些多边形的面积?
答:可以计算长方形和正方形的面积。
答:正方形是长方形推导出来的,长方形是平行四边形推导出来的,他们三个之间有联系。
问:为什么梯形的面积公式可以计算长方形和正方形的面积?
答:两个梯形可以变成平行四边形,平行四边形面积是由长方形推导出来的,长方形是由正方形转化的,正方形就是特殊的长方形。
问:为什么梯形的面积公式可以计算长方形和正方形的面积?
三角形
长方形
梯形
平行四边形
S=ah÷2
S=ab
S=ah
S=(a+b)×h÷2
三角形
长方形
梯形
平行四边形
S=ah÷2
S=ab
S=ah
S=(a+b)×h÷2
要想利用这些面积公式来计算它们的面积,必须要知道哪两个条件?
需要知道这些图形的底和高。
平行四边形
平行四边形
高度相等
观察这两个平行四边形,你有什么发现?
等底等高
观察这两个平行四边形,你有什么发现?
平行四边形的底相等,高也相等。
等底等高
平行四边形
平行四边形
等底等高
观察这两个平行四边形,你有什么发现?
面积相等
形状不同
三角形
三角形
等底等高
观察这两个三角形,你有什么发现?
观察这两个三角形,你有什么发现?
两个三角形的底相等,高也相等。
三角形
三角形
观察这两个三角形,你有什么发现?
等底等高
面积相等
形状不同
总结你的发现
三角形
三角形
平行四边形
平行四边形
等底等高的两个三角形或者平行四边形,它们的面积相等,但是形状不一定相同。
等底等高的两个三角形或者平行四边形,它们的面积相等,但是形状不一定相同。
总结你的发现
长方形
平行四边形
长方形与平行四边形,它们有什么关系?
宽
底
长
高
等底等高
面积相等
6厘米
12厘米
72平方厘米
长方形
平行四边形
宽
底
长
高
6厘米
12厘米
72平方厘米
等底等高的图形,面积是不会变的。
长方形与平行四边形,它们有什么关系?
等底等高
一样大
仔细观察,两个蓝色的面积哪个大?
一样大
仔细观察,两个蓝色的面积哪个大?
相等
仔细观察,两个蓝色的面积哪个大?
这两个三角形一直都是等底等高的。
相等
去掉公共的部分,剩下的蓝色部分面积怎么样?
相等
去掉公共的部分,剩下的蓝色部分面积怎么样?
等底等高的两个多边形面积相等。
周长没变。
如果多边形的面积增大或者减少,又与它们的底和高,有什么关系呢?
长:14.4厘米
宽:7.7厘米
高变小,底没变。
周长没变。
如果多边形的面积增大或者减少,又与它们的底和高,有什么关系呢?
长:14.4厘米
宽:7.7厘米
高变长,面积也变大。
底没变,高变长,面积变大。
底没变,高变长,面积变大。
高变短,底没变,面积缩小。
三角形底不变时,高变长或者是变短,它的面积也会随之变大或者是减小。
底不变时,面积随着高的变化而变化。
高没变,底变长,面积变大。
高不变时,面积随着底的变化而变化。
高没变,底变短,面积随之变小。
它们的底和高都是正方形的边长。
A
B
C
D
E
F
三角形ABC和三角形DEF,哪个面积大?
它们的面积一样大。
它们是等底等高的。
A
B
C
D
E
F
三角形ABC和三角形DEF,哪个面积大?
面积相同。
A
B
C
三角形ABC和三角形DEF,哪个面积大?
E
F
D
三角形DEF的面积变大了。
面积比之前大一倍。
因为它的底从一个小格挪到了第二个小格,它的底扩大到了原来的底的两倍。
三角形
长方形
梯形
平行四边形
S=ah÷2
S=ab
S=ah
S=(a+b)×h÷2
这些圆木,一共有多少根?
用数一数的办法,数出来这些原木有多少根。
可以用数层数的方法,先数出原木的上层是6根,再数出它的层数是4层,然后用四层乘6,等于24根。
这些圆木,一共有多少根?
每层的根数
×层数
每层的根数与层数,和这个长方形,有什么关系?
长方形
圆木的层数就是长方形的长和宽。
长:6
宽:4
这个长方形的面积,是多少?
长方形
6×4=24
长:6
宽:4
长方形的面积与长方形算出来的根数,有什么关系?
长:6
宽:4
相等
横截面是长方形的圆木,可以用长方形的面积公式,去算它们的面积。
这些圆木,一共有多少根?
这些圆木,一共有多少根?
(2+6)×5÷2
=8×5÷2
=40÷2
=20
2表示圆木顶层的根数,
6表示圆木的底层的根数,
5表示圆木的层数。
这些圆木,一共有多少根?
5
2
6
20根
这些圆木,一共有多少根?
20根
(2+6)×5÷2
=8×5÷2
=40÷2
=20
这些圆木,一共有多少根?
这些圆木,一共有多少根?
(1+6)×6÷2
=7×6÷2
=42÷2
=21
S=ah÷2
=6×6÷2
=36÷2
=18
21根
上底为0的时候,可以把它看成三角形。
这些圆木,一共有多少根?
21根
6
1
6
计算像这样的圆木堆它的方法。
21根
6
1
6
用它的顶层根数再加上它的底层根数,再乘层数,再除以2。
计算像这样的圆木堆它的方法。
21根
6
1
6
梯形的面积公式
总根数=(顶层根数+底层根数)×层数÷2
利用梯形的面积公式,还可以计算什么?
梯形的面积公式
总根数=(顶层根数+底层根数)×层数÷2
用梯形的面积公式,还可以计算火箭。
观察一下,每一层的根数,你有什么发现?
21根
6
1
6
连续的自然数字
前一层的根数比上一层的根数少1。
利用梯形的面积公式,还可以计算什么?
梯形的面积公式
总根数=(顶层根数+底层根数)×层数÷2
梯形的面积公式,除了可以计算圆木堆的总根数,还可以计算,连续算数的和。
三角形没有底,长方形没有宽,梯形没有上底。
都是一样长,都是8厘米。
10cm
40cm
8cm
16cm
8cm
8cm
可以分割的图形:___________________
三角形、长方形、梯形
组合图形的面积:__________________
可以分割的图形:___________________
10cm
40cm
8cm
16cm
三角形、长方形、梯形
S=ah÷2
=10×8÷2
=10×4
=40(cm2)
8cm
8cm
组合图形的面积:__________________
S=ah
=40×8
=320(cm2)
S=(a+b)h÷2
=(16+8)×8÷2
=24×8÷2
=96(cm2)
40+320+96
=456(cm2)
两个直角三角形的面积加起来,就是正方形的面积。
计算阴影部分的面积
5cm
4cm
S=(ah÷2)+(ah÷2)
=(5×4÷2)+(4×4÷2)
=10+8
=18(cm2)
计算阴影部分的面积
它的上底是4厘米,下底是5厘米,高是5厘米。
S=(a+b)h÷2
=(4+5)×4÷2
=9×4÷2
=9×2
=18(cm2)
5cm
4cm
计算阴影部分的面积
把这个图形看成一个平行四边形。
20(cm2)
它的上底是4厘米,下底是5厘米,不相等。
5cm
4cm
梯形的面积公式,可以帮我们解决圆木的问题;
课堂小结
梯形的面积,既可以推断平行四边形的面积,还可以推断三角形的面积;
梯形的面积公式,可以计算连续的层数;
等底等高的三角形和平行四边形,它们的面积相同,但是形状不一定一样;
课堂小结
计算阴影部分的面积;
可以把阴影部分,分成两个三角形来计算,也可以把阴影部分,看成一个梯形来计算。
再见!
