五年级下册数学教案-7.2 相遇问题 北师大版
文档属性
| 名称 | 五年级下册数学教案-7.2 相遇问题 北师大版 | 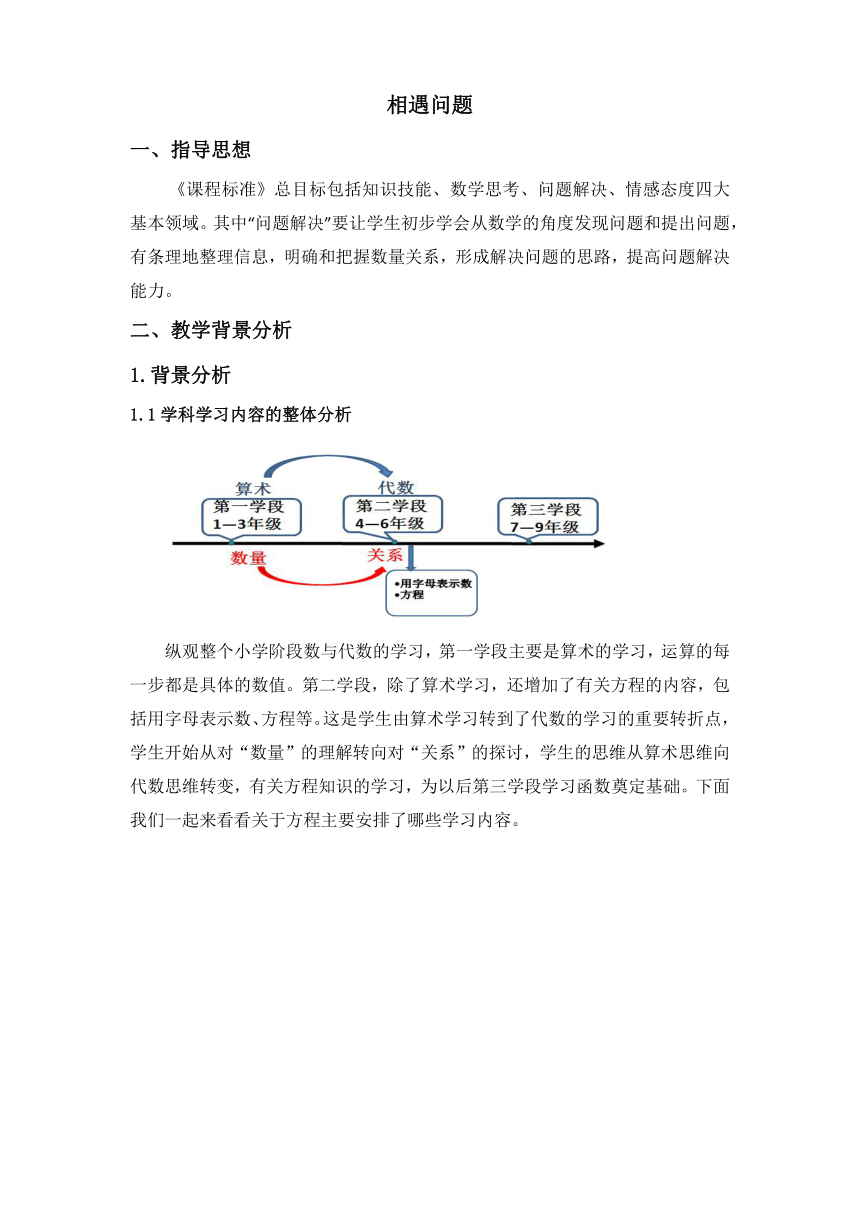 | |
| 格式 | docx | ||
| 文件大小 | 426.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 10:22:38 | ||
图片预览



文档简介
相遇问题
一、指导思想
《课程标准》总目标包括知识技能、数学思考、问题解决、情感态度四大基本领域。其中“问题解决”要让学生初步学会从数学的角度发现问题和提出问题,有条理地整理信息,明确和把握数量关系,形成解决问题的思路,提高问题解决能力。
二、教学背景分析
1.背景分析
1.1学科学习内容的整体分析
纵观整个小学阶段数与代数的学习,第一学段主要是算术的学习,运算的每一步都是具体的数值。第二学段,除了算术学习,还增加了有关方程的内容,包括用字母表示数、方程等。这是学生由算术学习转到了代数的学习的重要转折点,学生开始从对“数量”的理解转向对“关系”的探讨,学生的思维从算术思维向代数思维转变,有关方程知识的学习,为以后第三学段学习函数奠定基础。下面我们一起来看看关于方程主要安排了哪些学习内容。
从上面的图表中我们可以看出,方程的学习是从刻画现实世界的数量关系开始,抽象到数学中的数量关系,最后利用数量之间的关系解决生活中的问题。本单元以及六上解决简单百分数的问题都属于问题解决的范畴。
教材是如何呈现的呢?我又对两个版本的教材进行了对比。
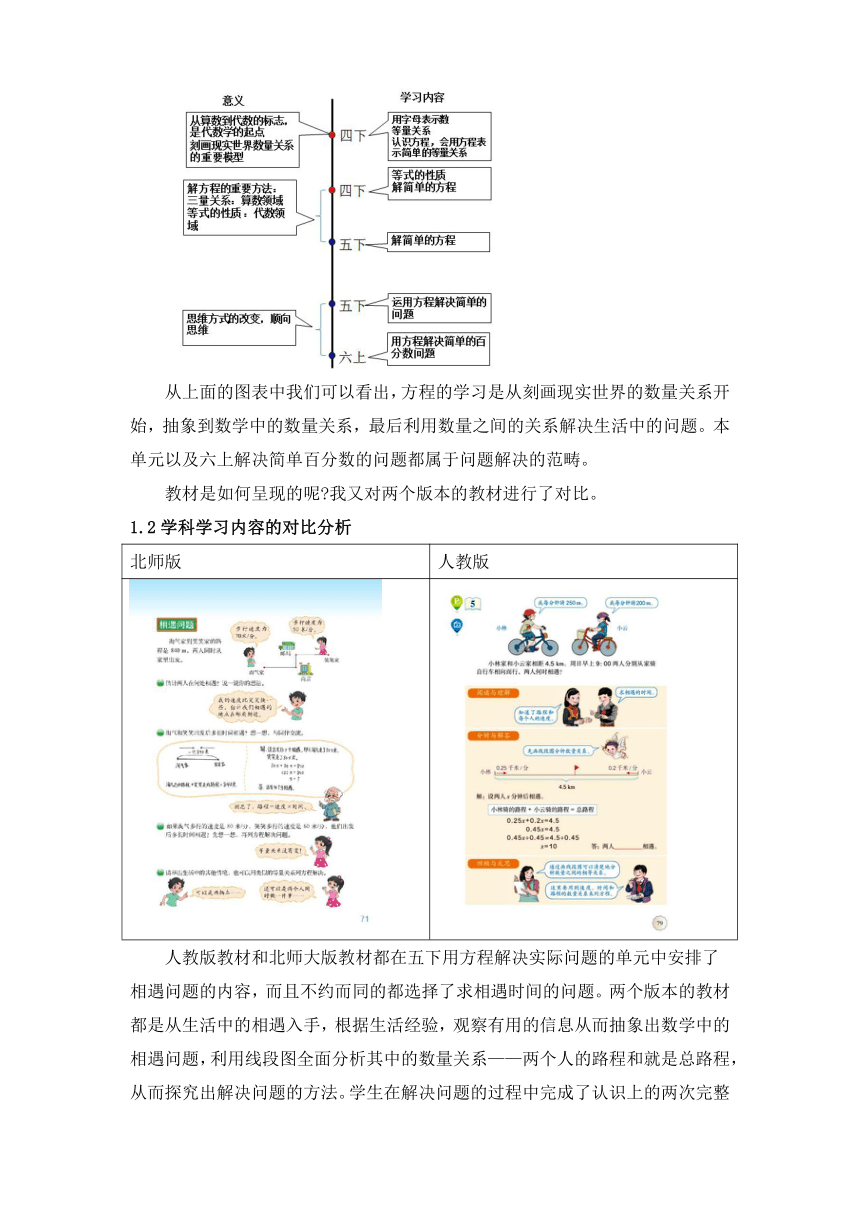
1.2学科学习内容的对比分析
北师版
人教版
人教版教材和北师大版教材都在五下用方程解决实际问题的单元中安排了相遇问题的内容,而且不约而同的都选择了求相遇时间的问题。两个版本的教材都是从生活中的相遇入手,根据生活经验,观察有用的信息从而抽象出数学中的相遇问题,利用线段图全面分析其中的数量关系——两个人的路程和就是总路程,从而探究出解决问题的方法。学生在解决问题的过程中完成了认识上的两次完整的转化。
北师大版教材与人教版教材不同的是北师大版教材在探究出解决问题的方法后,进而引导学生积累类似的问题原型,培养学生的应用意识。
1.3教学内容分析
北师大版教材在相遇问题这一课中设计了这样的4个问题:
①让学生根据两人的速度信息进行估计,在哪个地方相遇。
通过估一估,让学生初步体会速度的快慢会影响他们见面的地点。
②用方程解决相遇问题中求相遇时间的问题。
③变换两人步行的速度,再列方程解决相遇时间的问题
在解决相遇时间这个问题时,教材更改了淘气和笑笑的步行速度,让学生感悟到速度在变,但是速度、路程和时间这三个量之间的关系却没有变。
④积累生活中用类似等量关系列方程解决的原型问题
之后引导学生思考还有哪些类似的问题可以用这样的等量关系解决,积累分析数量关系并把实际问题抽象为方程的经验,经历建模的过程。思维方式结构化、 由变到不变体现一般化。
1.4 基于教材分析的思考
1、教材为什么安排从情境到数学问题,再到解决问题这样的两次转化呢?每次转化又有什么不同呢?
2、从整体上看,本节课中方程的应用是明线,重在引导学生进行算数思维和代数思维的转换,建模的思想是暗线,重在感悟数量关系的形成过程。如何培养学生的模型思想,是我们重点要考虑的问题。
1.5 学情分析
学生是怎么理解相遇的?在解决相遇问题时又有哪些困难?基于此,我们进行了如下调研。
调研题目1:
什么是相遇?
调研班级:五(8)班40名学生
学生理解的相遇只是生活中的相遇,碰到一起了,或者是见面了。
生活中的相遇学生都理解,那数学上的相遇问题学生是不是理解呢?带着这样的疑惑,我们又进行了如下的调研。
调研题目2:
调研班级:五(8)班40名学生
淘气和笑笑要见面,他们可能在哪点见面?为什么?
2209805715淘气家
笑笑家
淘气家
笑笑家
调研结果:
淘气家或笑笑家
中点
拐点
任意点
人数
2
31
5
2
百分数
5%
77.5%
12.5%
5%
结果分析:5%的学生选择在淘气家或者笑笑家见面,77.5%的学生选择在中点相遇,12.5%的学生选择在拐点相遇,5%的学生选择任一点相遇。
这些数据和现象的背后到底说明了什么呢?
77.5%的学生认为速度一样、路程一样,在中点相遇;12.5%的学生认为速度不一样,路程不一样,但是在拐点相遇;他们关注的是速度\路程存在特殊关系是的相遇,选择中点的学生考虑路程\速度固定,选择拐点的学生考虑两者之间成特殊关系.而选择在任意点相遇的5%学生,他们关注到了速度、路程任意条件下的相遇。这说明多数的学生对于数学上相遇问题的理解是零散的、片面的(呈点状的),如何让学生能够系统的(呈线状的)理解数学上的相遇,值得我们思考。
为了了解学生是怎么解决问题的,以及在解决问题的过程中又有哪些经验,我们接着进行如下调研:
调研题目3
淘气和笑笑同时出发,相向而行,他们出发后经过多长时间相遇?
33083565405淘气家
笑笑家
淘气家
笑笑家
所有的学生拿到问题后都很茫然,不知所措,用他们自己的话来说就是有点懵了。通过访谈,得知学生不知所措的原因是路程、速度什么信息都没有,怎么得到相遇时间呢。
分析:不给任何信息的情况下,学生不知道怎么入手去解决问题,学生调动以前所学的知识,想到与时间有关的量有路程和速度。
那在无数据的情况下,学生是怎么做的呢?
调研班级:五(8)班40名学生
调研结果:
假设
不敢假设
设数
分段
数量关系
随便设数-尝试解决-方法
随便设数-背公式
根据生活经验设数
人数
20
8
4
2
2
4
百分比
50%
20%
10%
5%
5%
10%
结果分析:
从表中,我们可以看出,在没有数据的情况下,90%的学生能够在“无路可走”时想到假设数据。其中50%的学生能够假设路程和淘气笑笑的速度,利用速度、时间和路程之间的关系,尝试解决问题。有20%的学生设数后直接利用公式解决问题。还有10%的学生根据生活经验,确定淘气和笑笑1分钟走的路程(即他们的速度);2名学生选择分段的方法,还有4名同学不知道该怎么办,没有想法。只有2名学生想到数量关系。
我们发现,大部分学生在没有数据的情况下,想到了假设的方法。假设法是一种很好地学习方法,在出现复杂问题时假设法能够收到“绝处逢生”的效果,通过假设,使题中的数量关系清晰化,帮助学生很快的找到解决问题的突破口,丰富学生的想象力,激发其创造意识。但是其中有80%的学生用的是设数的方法,只有10的学生想到直接利用数量之间的关系解决问题。从利用设数解决一个问题到利用关系解决一类问题,需要引导学生进行深入的思考。
我的思考:
1、借助情境,让学生从已有的生活经验出发,亲身经历将实际问题抽象出数学问题,进而解决问题并应用的过程。在这个过程中,重点让学生体会数量关系的形成过程,也就是建模的过程。
2、通过设计具有思维挑战性的问题,在从无数据到有数据的过程中,发展学生发现问题和提出问题的能力。
教学目标
1、由生活中的相遇抽象出数学中的相遇问题,通过观察、假设、分析等一系列的探究活动,让学生经历数量关系的形成过程,提高用方程解决简单实际问题的能力。
2、经历解决实际问题的过程,体验数学与日常生活密切相关,提高收集信息、处理信息和建立模型的能力。
教学重点
经历发现问题、提出问题、解决实际问题的过程,在这个过程中,体会模型思想,提高用方程解决问题的能力。
教学难点
经历由无数据到有数据,探究数量关系的形成过程,提高解决实际问题的能力。
教学过程
(一)从生活中的相遇问题出发,初步体会什么是相遇。
82867551435淘气家
笑笑家
淘气家
笑笑家
这是我们的老朋友淘气和笑笑,他们都非常喜欢阅读书籍。这个周末他们打算聚在一起交流一下各自的读书心得,还想推荐一本好书送给对方呢!这是淘气家的位置,这是笑笑家的位置,这是连接他们两家的道路。想一想他们会约在哪儿见面呢?
有想法了,那赶快与同伴交流一下你的想法,并说说你的理由。
谁来说说你觉得他们会约在哪儿见面?
预设:1、在中间见面,这样两个人走的路程一样,比较公平。
(从路程相等的角度考虑,选择了中间点)
2、让淘气走全程,笑笑在家等着。
还有不同的想法吗?
3、在拐点见面。可以吗?他是怎么想的?
淘气的速度快,笑笑的速度慢,这样淘气会多走一些。
速度快就多走一些,其实他默认了两个人的什么是一样的?
同时是什么意思?
他说的给了你什么启发?想一想,还可能在哪见面?
(在路上的任何一点都有可能。)
什么意思,能说说你的想法吗?
现在你们觉得什么会直接影响见面的地点?(两个人的速度)
小结:正因为两个人速度的不确定性,所以同学们选择的任何一个地点都有可能是他们的见面地点。
(二)走进同时出发的相遇问题,再次体会相遇的内涵
淘气和笑笑就像大家想的这样,他们是同时出发的,想一想:他们可能多长时间在你希望的那点相遇呢?与你的同伴讨论一下你打算怎么解决这个问题。然后把你的想法记录在学习单中。
有想法了吗?遇到什么困难了?是啊!没有我们想要的这些信息,你们打算怎么办啊?
预设:假设出速度和路程想办法得到时间。
还有不同的想法吗?
老师觉得你们遇到困难时,也可以借助老师提供的图来帮助你理解。有想法了吗?那就赶快开始吧!
完成以后在小组里交流一下你的想法。
一起看看这几个同学的想法。能看懂他们是怎么想的吗?他们都得到多长时间相遇了吗?
预设:1、先解决分别假设路程和速度的(可能有)
说说你是怎么想的?每个算式表示什么意思?
这是淘气用的时间,这是笑笑用的时间,怎么知道他们多长时间相遇啊?为什么?
2、解决假设总路程和速度的(2个)
画图
谁能看懂他是怎么想的?或者你有什么疑问?
怎么看出他们多长时间相遇了?你能在图上指一指吗?每个格表示什么意思?
设数
速度和——2+3表示什么意思啊?他俩能相加吗?为什么?能在线段图上画画,让我们更清楚的理解你的意思吗?走到哪儿就行了?
谁理解他的意思了?你能用这不同颜色的纸条分别代表淘气和笑笑的速度再解释一下这个方法吗?
(有几个这样的路程就走多长时间)
小结:淘气每分钟这么多,笑笑每分钟走这么多,他俩一分钟一共走了这么多,再走1分钟,两个人合起来又走了这么多,我们只要知道总路程中有几个这样的每分钟走得路程和,就知道几分钟相遇了。其实每分钟走得路程和就是你们说的速度和。
3、方程的方法
方程中的每一个数表示什么意思啊!这个方程表达了什么意思?
还有不同的方法吗?那你的方法和几一样?你的呢?有和他的方法一样的吗?(另一种)
我得找大家评评理,明明都不一样啊!速度不同,得到的相遇时间也不同,他们就说是一样的,你们觉得一样吗?为什么?
总路程÷(淘气的速度+笑笑的速度)=相遇时间
能结合黑板上的图解释一下你的意思吗?
那这些呢?这些更不一样了?
那能结合图说说吗?
你们这么解释我有点明白了,其实你们看他们一样不一样不是关注这些具体的数据是否一样,而是透过这些数据看到了他们的本质都是运用了总路程÷(淘气的速度+笑笑的速度)=相遇时间和淘气路程+笑笑路程=总路程这两个关系解决问题的。我的理解对吗?
你们太厉害了,已经不再被表象迷惑,能透过现象看问题的本质了,老师得向你们学习。
所以你们还有了这样的表达S÷(A+B)=T。谁能说说他表达了哪个关系?
淘气路程+笑笑路程=总路程,你能用字母表达这个关系吗?
孩子们你们太棒了,你们的研究也带给我很多思考,我们一起来回顾一下整个的研究历程,能说说我们是怎么解决这个问题的吗?
预设: 先假设数据在寻找这些量之间的关系
从最开始只有一条路线,求相遇的时间,大家觉得这是一个不可能完成的任务,到大家想办法自己增加了一些数据,借助了图的帮助,寻找到了解决这个问题的那些量之间的关系,从而找到了解决这个问题的本质。
(三)思考相遇问题的本质, 梳理一类问题的数学模型
想一想,生活中有哪些情境,也可以用类似的等量关系解决?
老师也找了一些问题,你能判断一下这样问题能用我们今天找到的等量关系解决吗?可以用哪个?
为什么你们觉得他们都能用这两个等量关系解决?
你觉得他们相同点在哪?(两个人同时,共同完成一件事)
今天,我们发现我们不仅能解决相遇问题,还能解决和相遇问题相类似的很多问题,正是因为这些问题他们背后的关系是一样的。
三、设计特色
在解决问题的过程中,让学生经历认识上的两次转化。第一次转化是从生活中的相遇抽象出数学中的相遇问题,关注学生发现问题和提出问题的过程;第二次转化是根据抽象出的数学问题,全面分析其中的数量关系,解决问题并加以应用,重视“数量关系的形成”这个重要的数学建模的过程。
一、指导思想
《课程标准》总目标包括知识技能、数学思考、问题解决、情感态度四大基本领域。其中“问题解决”要让学生初步学会从数学的角度发现问题和提出问题,有条理地整理信息,明确和把握数量关系,形成解决问题的思路,提高问题解决能力。
二、教学背景分析
1.背景分析
1.1学科学习内容的整体分析
纵观整个小学阶段数与代数的学习,第一学段主要是算术的学习,运算的每一步都是具体的数值。第二学段,除了算术学习,还增加了有关方程的内容,包括用字母表示数、方程等。这是学生由算术学习转到了代数的学习的重要转折点,学生开始从对“数量”的理解转向对“关系”的探讨,学生的思维从算术思维向代数思维转变,有关方程知识的学习,为以后第三学段学习函数奠定基础。下面我们一起来看看关于方程主要安排了哪些学习内容。
从上面的图表中我们可以看出,方程的学习是从刻画现实世界的数量关系开始,抽象到数学中的数量关系,最后利用数量之间的关系解决生活中的问题。本单元以及六上解决简单百分数的问题都属于问题解决的范畴。
教材是如何呈现的呢?我又对两个版本的教材进行了对比。
1.2学科学习内容的对比分析
北师版
人教版
人教版教材和北师大版教材都在五下用方程解决实际问题的单元中安排了相遇问题的内容,而且不约而同的都选择了求相遇时间的问题。两个版本的教材都是从生活中的相遇入手,根据生活经验,观察有用的信息从而抽象出数学中的相遇问题,利用线段图全面分析其中的数量关系——两个人的路程和就是总路程,从而探究出解决问题的方法。学生在解决问题的过程中完成了认识上的两次完整的转化。
北师大版教材与人教版教材不同的是北师大版教材在探究出解决问题的方法后,进而引导学生积累类似的问题原型,培养学生的应用意识。
1.3教学内容分析
北师大版教材在相遇问题这一课中设计了这样的4个问题:
①让学生根据两人的速度信息进行估计,在哪个地方相遇。
通过估一估,让学生初步体会速度的快慢会影响他们见面的地点。
②用方程解决相遇问题中求相遇时间的问题。
③变换两人步行的速度,再列方程解决相遇时间的问题
在解决相遇时间这个问题时,教材更改了淘气和笑笑的步行速度,让学生感悟到速度在变,但是速度、路程和时间这三个量之间的关系却没有变。
④积累生活中用类似等量关系列方程解决的原型问题
之后引导学生思考还有哪些类似的问题可以用这样的等量关系解决,积累分析数量关系并把实际问题抽象为方程的经验,经历建模的过程。思维方式结构化、 由变到不变体现一般化。
1.4 基于教材分析的思考
1、教材为什么安排从情境到数学问题,再到解决问题这样的两次转化呢?每次转化又有什么不同呢?
2、从整体上看,本节课中方程的应用是明线,重在引导学生进行算数思维和代数思维的转换,建模的思想是暗线,重在感悟数量关系的形成过程。如何培养学生的模型思想,是我们重点要考虑的问题。
1.5 学情分析
学生是怎么理解相遇的?在解决相遇问题时又有哪些困难?基于此,我们进行了如下调研。
调研题目1:
什么是相遇?
调研班级:五(8)班40名学生
学生理解的相遇只是生活中的相遇,碰到一起了,或者是见面了。
生活中的相遇学生都理解,那数学上的相遇问题学生是不是理解呢?带着这样的疑惑,我们又进行了如下的调研。
调研题目2:
调研班级:五(8)班40名学生
淘气和笑笑要见面,他们可能在哪点见面?为什么?
2209805715淘气家
笑笑家
淘气家
笑笑家
调研结果:
淘气家或笑笑家
中点
拐点
任意点
人数
2
31
5
2
百分数
5%
77.5%
12.5%
5%
结果分析:5%的学生选择在淘气家或者笑笑家见面,77.5%的学生选择在中点相遇,12.5%的学生选择在拐点相遇,5%的学生选择任一点相遇。
这些数据和现象的背后到底说明了什么呢?
77.5%的学生认为速度一样、路程一样,在中点相遇;12.5%的学生认为速度不一样,路程不一样,但是在拐点相遇;他们关注的是速度\路程存在特殊关系是的相遇,选择中点的学生考虑路程\速度固定,选择拐点的学生考虑两者之间成特殊关系.而选择在任意点相遇的5%学生,他们关注到了速度、路程任意条件下的相遇。这说明多数的学生对于数学上相遇问题的理解是零散的、片面的(呈点状的),如何让学生能够系统的(呈线状的)理解数学上的相遇,值得我们思考。
为了了解学生是怎么解决问题的,以及在解决问题的过程中又有哪些经验,我们接着进行如下调研:
调研题目3
淘气和笑笑同时出发,相向而行,他们出发后经过多长时间相遇?
33083565405淘气家
笑笑家
淘气家
笑笑家
所有的学生拿到问题后都很茫然,不知所措,用他们自己的话来说就是有点懵了。通过访谈,得知学生不知所措的原因是路程、速度什么信息都没有,怎么得到相遇时间呢。
分析:不给任何信息的情况下,学生不知道怎么入手去解决问题,学生调动以前所学的知识,想到与时间有关的量有路程和速度。
那在无数据的情况下,学生是怎么做的呢?
调研班级:五(8)班40名学生
调研结果:
假设
不敢假设
设数
分段
数量关系
随便设数-尝试解决-方法
随便设数-背公式
根据生活经验设数
人数
20
8
4
2
2
4
百分比
50%
20%
10%
5%
5%
10%
结果分析:
从表中,我们可以看出,在没有数据的情况下,90%的学生能够在“无路可走”时想到假设数据。其中50%的学生能够假设路程和淘气笑笑的速度,利用速度、时间和路程之间的关系,尝试解决问题。有20%的学生设数后直接利用公式解决问题。还有10%的学生根据生活经验,确定淘气和笑笑1分钟走的路程(即他们的速度);2名学生选择分段的方法,还有4名同学不知道该怎么办,没有想法。只有2名学生想到数量关系。
我们发现,大部分学生在没有数据的情况下,想到了假设的方法。假设法是一种很好地学习方法,在出现复杂问题时假设法能够收到“绝处逢生”的效果,通过假设,使题中的数量关系清晰化,帮助学生很快的找到解决问题的突破口,丰富学生的想象力,激发其创造意识。但是其中有80%的学生用的是设数的方法,只有10的学生想到直接利用数量之间的关系解决问题。从利用设数解决一个问题到利用关系解决一类问题,需要引导学生进行深入的思考。
我的思考:
1、借助情境,让学生从已有的生活经验出发,亲身经历将实际问题抽象出数学问题,进而解决问题并应用的过程。在这个过程中,重点让学生体会数量关系的形成过程,也就是建模的过程。
2、通过设计具有思维挑战性的问题,在从无数据到有数据的过程中,发展学生发现问题和提出问题的能力。
教学目标
1、由生活中的相遇抽象出数学中的相遇问题,通过观察、假设、分析等一系列的探究活动,让学生经历数量关系的形成过程,提高用方程解决简单实际问题的能力。
2、经历解决实际问题的过程,体验数学与日常生活密切相关,提高收集信息、处理信息和建立模型的能力。
教学重点
经历发现问题、提出问题、解决实际问题的过程,在这个过程中,体会模型思想,提高用方程解决问题的能力。
教学难点
经历由无数据到有数据,探究数量关系的形成过程,提高解决实际问题的能力。
教学过程
(一)从生活中的相遇问题出发,初步体会什么是相遇。
82867551435淘气家
笑笑家
淘气家
笑笑家
这是我们的老朋友淘气和笑笑,他们都非常喜欢阅读书籍。这个周末他们打算聚在一起交流一下各自的读书心得,还想推荐一本好书送给对方呢!这是淘气家的位置,这是笑笑家的位置,这是连接他们两家的道路。想一想他们会约在哪儿见面呢?
有想法了,那赶快与同伴交流一下你的想法,并说说你的理由。
谁来说说你觉得他们会约在哪儿见面?
预设:1、在中间见面,这样两个人走的路程一样,比较公平。
(从路程相等的角度考虑,选择了中间点)
2、让淘气走全程,笑笑在家等着。
还有不同的想法吗?
3、在拐点见面。可以吗?他是怎么想的?
淘气的速度快,笑笑的速度慢,这样淘气会多走一些。
速度快就多走一些,其实他默认了两个人的什么是一样的?
同时是什么意思?
他说的给了你什么启发?想一想,还可能在哪见面?
(在路上的任何一点都有可能。)
什么意思,能说说你的想法吗?
现在你们觉得什么会直接影响见面的地点?(两个人的速度)
小结:正因为两个人速度的不确定性,所以同学们选择的任何一个地点都有可能是他们的见面地点。
(二)走进同时出发的相遇问题,再次体会相遇的内涵
淘气和笑笑就像大家想的这样,他们是同时出发的,想一想:他们可能多长时间在你希望的那点相遇呢?与你的同伴讨论一下你打算怎么解决这个问题。然后把你的想法记录在学习单中。
有想法了吗?遇到什么困难了?是啊!没有我们想要的这些信息,你们打算怎么办啊?
预设:假设出速度和路程想办法得到时间。
还有不同的想法吗?
老师觉得你们遇到困难时,也可以借助老师提供的图来帮助你理解。有想法了吗?那就赶快开始吧!
完成以后在小组里交流一下你的想法。
一起看看这几个同学的想法。能看懂他们是怎么想的吗?他们都得到多长时间相遇了吗?
预设:1、先解决分别假设路程和速度的(可能有)
说说你是怎么想的?每个算式表示什么意思?
这是淘气用的时间,这是笑笑用的时间,怎么知道他们多长时间相遇啊?为什么?
2、解决假设总路程和速度的(2个)
画图
谁能看懂他是怎么想的?或者你有什么疑问?
怎么看出他们多长时间相遇了?你能在图上指一指吗?每个格表示什么意思?
设数
速度和——2+3表示什么意思啊?他俩能相加吗?为什么?能在线段图上画画,让我们更清楚的理解你的意思吗?走到哪儿就行了?
谁理解他的意思了?你能用这不同颜色的纸条分别代表淘气和笑笑的速度再解释一下这个方法吗?
(有几个这样的路程就走多长时间)
小结:淘气每分钟这么多,笑笑每分钟走这么多,他俩一分钟一共走了这么多,再走1分钟,两个人合起来又走了这么多,我们只要知道总路程中有几个这样的每分钟走得路程和,就知道几分钟相遇了。其实每分钟走得路程和就是你们说的速度和。
3、方程的方法
方程中的每一个数表示什么意思啊!这个方程表达了什么意思?
还有不同的方法吗?那你的方法和几一样?你的呢?有和他的方法一样的吗?(另一种)
我得找大家评评理,明明都不一样啊!速度不同,得到的相遇时间也不同,他们就说是一样的,你们觉得一样吗?为什么?
总路程÷(淘气的速度+笑笑的速度)=相遇时间
能结合黑板上的图解释一下你的意思吗?
那这些呢?这些更不一样了?
那能结合图说说吗?
你们这么解释我有点明白了,其实你们看他们一样不一样不是关注这些具体的数据是否一样,而是透过这些数据看到了他们的本质都是运用了总路程÷(淘气的速度+笑笑的速度)=相遇时间和淘气路程+笑笑路程=总路程这两个关系解决问题的。我的理解对吗?
你们太厉害了,已经不再被表象迷惑,能透过现象看问题的本质了,老师得向你们学习。
所以你们还有了这样的表达S÷(A+B)=T。谁能说说他表达了哪个关系?
淘气路程+笑笑路程=总路程,你能用字母表达这个关系吗?
孩子们你们太棒了,你们的研究也带给我很多思考,我们一起来回顾一下整个的研究历程,能说说我们是怎么解决这个问题的吗?
预设: 先假设数据在寻找这些量之间的关系
从最开始只有一条路线,求相遇的时间,大家觉得这是一个不可能完成的任务,到大家想办法自己增加了一些数据,借助了图的帮助,寻找到了解决这个问题的那些量之间的关系,从而找到了解决这个问题的本质。
(三)思考相遇问题的本质, 梳理一类问题的数学模型
想一想,生活中有哪些情境,也可以用类似的等量关系解决?
老师也找了一些问题,你能判断一下这样问题能用我们今天找到的等量关系解决吗?可以用哪个?
为什么你们觉得他们都能用这两个等量关系解决?
你觉得他们相同点在哪?(两个人同时,共同完成一件事)
今天,我们发现我们不仅能解决相遇问题,还能解决和相遇问题相类似的很多问题,正是因为这些问题他们背后的关系是一样的。
三、设计特色
在解决问题的过程中,让学生经历认识上的两次转化。第一次转化是从生活中的相遇抽象出数学中的相遇问题,关注学生发现问题和提出问题的过程;第二次转化是根据抽象出的数学问题,全面分析其中的数量关系,解决问题并加以应用,重视“数量关系的形成”这个重要的数学建模的过程。
