人教版八年级上册13.3.1 等腰三角形课件(24张PPT)
文档属性
| 名称 | 人教版八年级上册13.3.1 等腰三角形课件(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 326.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 11:05:47 | ||
图片预览



文档简介
13.3.1 等腰三角形
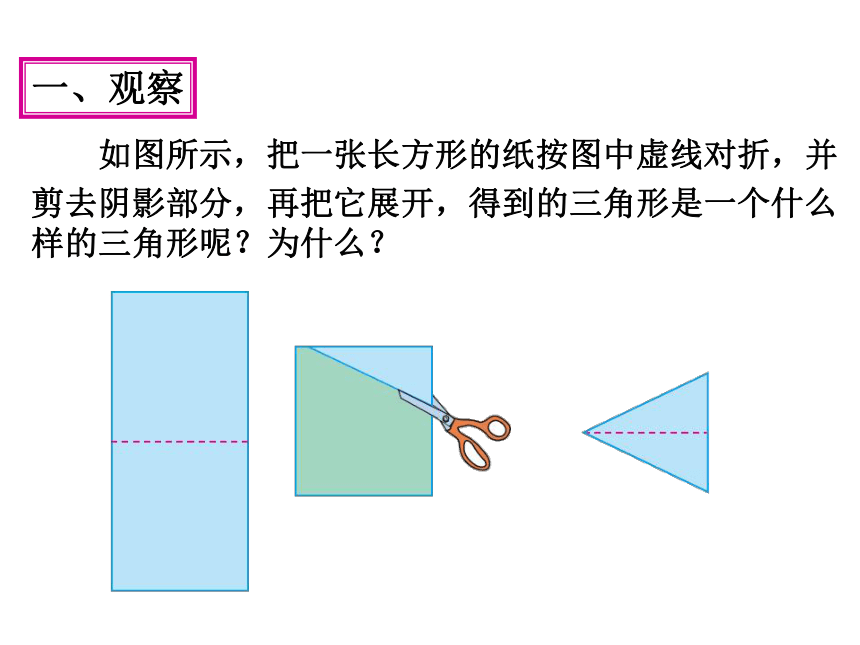
一、观察
如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的三角形是一个什么样的三角形呢?为什么?
二、等腰三角形的相关概念
1.你还记得什么样的三角形是等腰三角形吗?
定义:有两边相等的三角形是等腰三角形.
2.你还记得在等腰三角形中,各个边和角的名称吗?
腰
腰
底边
A
B
C
顶角
底角
三、探究等腰三角形的性质
A
B
C
D
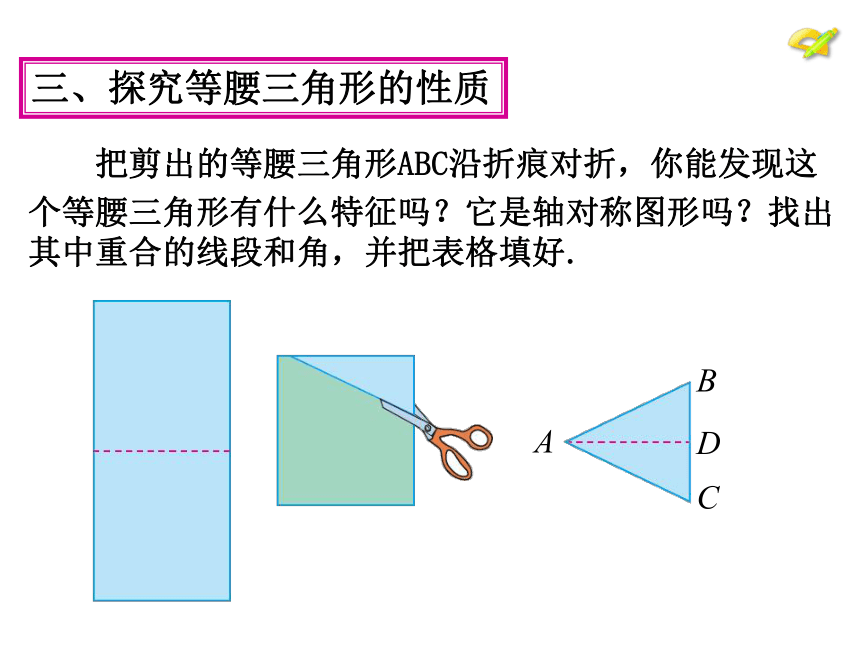
把剪出的等腰三角形ABC沿折痕对折,你能发现这
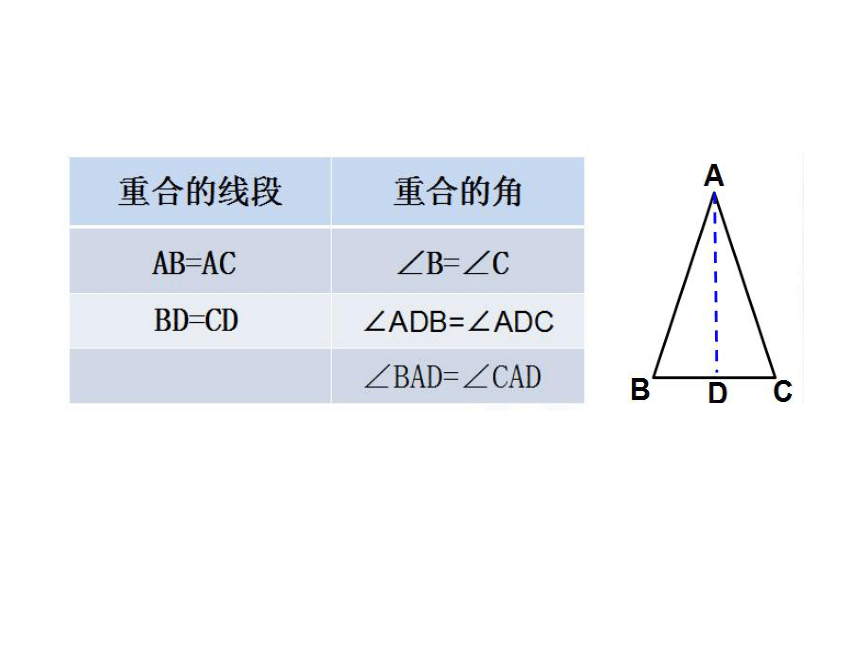
个等腰三角形有什么特征吗?它是轴对称图形吗?找出其中重合的线段和角,并把表格填好.
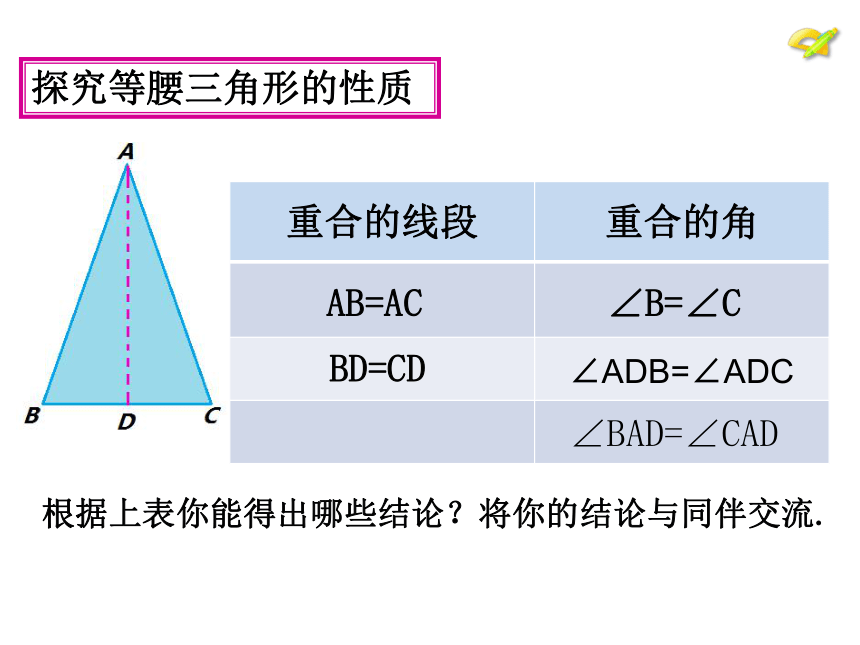
探究等腰三角形的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}重合的线段
重合的角
AB=AC
∠B=∠C
BD=CD
∠ADB=∠ADC
∠BAD=∠CAD
根据上表你能得出哪些结论?将你的结论与同伴交流.
(1)在△ABC中,若AB=AC,则 = .
猜想1
等腰三角形的两个底角相等;
任意等腰三角形都满足以上猜想吗?
探究等腰三角形的性质
∠B
∠C
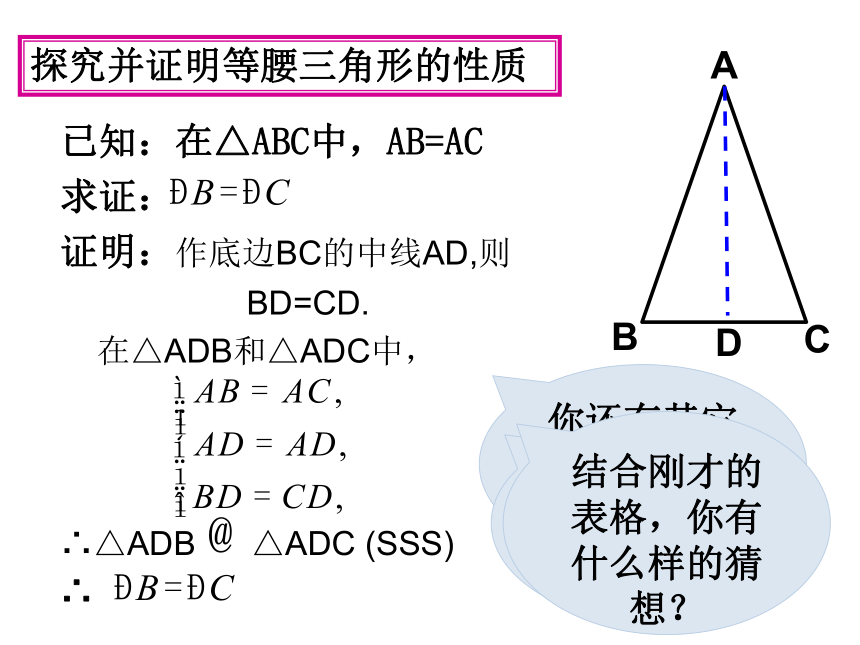
探究并证明等腰三角形的性质
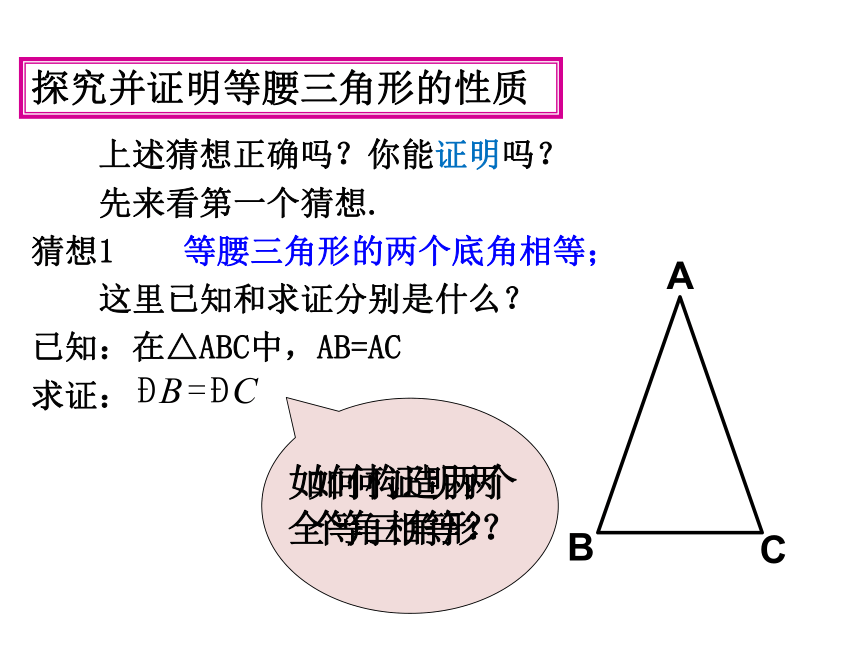
上述猜想正确吗?你能证明吗?
先来看第一个猜想.
猜想1 等腰三角形的两个底角相等;
这里已知和求证分别是什么?
已知:在△ABC中,AB=AC
求证:
A
B
C
如何证明两个角相等?
如何构造两个全等三角形?
探究并证明等腰三角形的性质
已知:在△ABC中,AB=AC
求证:
证明:作底边BC的中线AD,则
BD=CD.
在△ADB和△ADC中,
∴△ADB △ADC (SSS)
∴
A
B
C
D
你还有其它的证明方法吗?
你们所作的辅助线在一条直线上吗?
结合刚才的表格,你有什么样的猜想?
探究等腰三角形的性质
(1)AD可以看作是顶角的 , 或BC边上的 或BC边上的 .
平分线
中线
高
猜想2
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
任意等腰三角形都满足以上猜想吗?
探究并证明等腰三角形的性质
来看第二个猜想.
猜想2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
如何证明?这里已知和求证分别是什么?
已知:在△ABC中,AB=AC,
.
求证:AD是BC边上的中线,
AD是∠BAC的平分线.
只要证明BD=CD
只要证明∠BAD=∠CAD
包含了三个命题
探究并证明等腰三角形的性质
已知:在△ABC中,AB=AC, .
求证:AD是BC边上的中线,
AD是∠BAC的平分线.
证明:∵
∴
在Rt△ADB和Rt△ADC中,
∴Rt△ADB Rt△ADC.(HL)
∴BD=CD,
∠BAD=∠CAD,
即 AD是BC边上的中线,AD是∠BAC的平分线 .
只要证明BD=CD
只要证明∠BAD=∠CAD
探究等腰三角形的性质
通过折叠,你发现等腰三角形是一个什么样的图形?
轴对称图形
它的对称轴是什么?
底边上的中线(顶角平分线、底边上的高)所在的直线是它的对称轴.
性质1 等腰三角形的两个底角相等.
(简写成“等边对等角”)
几何语言
在△ABC中,
∵ AB=AC
∴ (等边对等角)
注意:必须在同一个三角形中.
探究并证明等腰三角形的性质
A
B
C
性质2 等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合.(简写成“三线合一”)
几何语言
在△ABC中,AB=AC
∵
∴BD=CD,
∠BAD=∠CAD(三线合一)
探究并证明等腰三角形的性质
练习
1. 下列说法中,正确的有( )
①有两边相等的三角形是等腰三角形;②等腰三角形的两底角相等;③等腰三角形的中线、高、角平分线互相重合;④等腰三角形是轴对称图形,对称轴是底边上的高.
A.1个 B.2个 C.3个 D.4个
B
2.如图,在下列等腰三角形中,分别求出题中要求的角的度数.
(1)如图,在△ABC中, AB =AC,
∠A =36°, 则∠B = °.
(2)如图,在△ABC中, AB =AC,
∠B =36°,则∠A= °.
练习
72
108
如图,已知AB=AC, ,垂足为D,∠BAC=100°,BC=8cm.
(1)求∠BAD的度数;
(2)求BD的长度.
练习
例题
例1 如图,△ABC 中,AB =AC,点D 在AC 上,
且BD =BC =AD.求△ABC 各角的度数.
A
B
C
D
(1) 等腰三角形的定义
(2)等腰三角形的性质
(3)本节课你学到了哪些证明线段相等或角相等的
方法?
课堂小结
书上习题13.3第6、7题.
布置作业
1.(1)等腰三角形的一个角是80°,它的另外两个角是多少度?
(2)等腰三角形的一个角是110°,它的另外两个是多少度?
补充练习
2. 在△ABC中,AB=AC, 于D,∠B=65°,
BC=6,则,BD= ,∠C= ,∠BAD= .
3.已知△ABC是等腰三角形,∠A+∠B=130°,求∠A的度数.
3
65°
25°
65°或80°
补充练习
补充练习
4.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.
求证:BD=CE
一、观察
如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的三角形是一个什么样的三角形呢?为什么?
二、等腰三角形的相关概念
1.你还记得什么样的三角形是等腰三角形吗?
定义:有两边相等的三角形是等腰三角形.
2.你还记得在等腰三角形中,各个边和角的名称吗?
腰
腰
底边
A
B
C
顶角
底角
三、探究等腰三角形的性质
A
B
C
D
把剪出的等腰三角形ABC沿折痕对折,你能发现这
个等腰三角形有什么特征吗?它是轴对称图形吗?找出其中重合的线段和角,并把表格填好.
探究等腰三角形的性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}重合的线段
重合的角
AB=AC
∠B=∠C
BD=CD
∠ADB=∠ADC
∠BAD=∠CAD
根据上表你能得出哪些结论?将你的结论与同伴交流.
(1)在△ABC中,若AB=AC,则 = .
猜想1
等腰三角形的两个底角相等;
任意等腰三角形都满足以上猜想吗?
探究等腰三角形的性质
∠B
∠C
探究并证明等腰三角形的性质
上述猜想正确吗?你能证明吗?
先来看第一个猜想.
猜想1 等腰三角形的两个底角相等;
这里已知和求证分别是什么?
已知:在△ABC中,AB=AC
求证:
A
B
C
如何证明两个角相等?
如何构造两个全等三角形?
探究并证明等腰三角形的性质
已知:在△ABC中,AB=AC
求证:
证明:作底边BC的中线AD,则
BD=CD.
在△ADB和△ADC中,
∴△ADB △ADC (SSS)
∴
A
B
C
D
你还有其它的证明方法吗?
你们所作的辅助线在一条直线上吗?
结合刚才的表格,你有什么样的猜想?
探究等腰三角形的性质
(1)AD可以看作是顶角的 , 或BC边上的 或BC边上的 .
平分线
中线
高
猜想2
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
任意等腰三角形都满足以上猜想吗?
探究并证明等腰三角形的性质
来看第二个猜想.
猜想2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
如何证明?这里已知和求证分别是什么?
已知:在△ABC中,AB=AC,
.
求证:AD是BC边上的中线,
AD是∠BAC的平分线.
只要证明BD=CD
只要证明∠BAD=∠CAD
包含了三个命题
探究并证明等腰三角形的性质
已知:在△ABC中,AB=AC, .
求证:AD是BC边上的中线,
AD是∠BAC的平分线.
证明:∵
∴
在Rt△ADB和Rt△ADC中,
∴Rt△ADB Rt△ADC.(HL)
∴BD=CD,
∠BAD=∠CAD,
即 AD是BC边上的中线,AD是∠BAC的平分线 .
只要证明BD=CD
只要证明∠BAD=∠CAD
探究等腰三角形的性质
通过折叠,你发现等腰三角形是一个什么样的图形?
轴对称图形
它的对称轴是什么?
底边上的中线(顶角平分线、底边上的高)所在的直线是它的对称轴.
性质1 等腰三角形的两个底角相等.
(简写成“等边对等角”)
几何语言
在△ABC中,
∵ AB=AC
∴ (等边对等角)
注意:必须在同一个三角形中.
探究并证明等腰三角形的性质
A
B
C
性质2 等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合.(简写成“三线合一”)
几何语言
在△ABC中,AB=AC
∵
∴BD=CD,
∠BAD=∠CAD(三线合一)
探究并证明等腰三角形的性质
练习
1. 下列说法中,正确的有( )
①有两边相等的三角形是等腰三角形;②等腰三角形的两底角相等;③等腰三角形的中线、高、角平分线互相重合;④等腰三角形是轴对称图形,对称轴是底边上的高.
A.1个 B.2个 C.3个 D.4个
B
2.如图,在下列等腰三角形中,分别求出题中要求的角的度数.
(1)如图,在△ABC中, AB =AC,
∠A =36°, 则∠B = °.
(2)如图,在△ABC中, AB =AC,
∠B =36°,则∠A= °.
练习
72
108
如图,已知AB=AC, ,垂足为D,∠BAC=100°,BC=8cm.
(1)求∠BAD的度数;
(2)求BD的长度.
练习
例题
例1 如图,△ABC 中,AB =AC,点D 在AC 上,
且BD =BC =AD.求△ABC 各角的度数.
A
B
C
D
(1) 等腰三角形的定义
(2)等腰三角形的性质
(3)本节课你学到了哪些证明线段相等或角相等的
方法?
课堂小结
书上习题13.3第6、7题.
布置作业
1.(1)等腰三角形的一个角是80°,它的另外两个角是多少度?
(2)等腰三角形的一个角是110°,它的另外两个是多少度?
补充练习
2. 在△ABC中,AB=AC, 于D,∠B=65°,
BC=6,则,BD= ,∠C= ,∠BAD= .
3.已知△ABC是等腰三角形,∠A+∠B=130°,求∠A的度数.
3
65°
25°
65°或80°
补充练习
补充练习
4.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.
求证:BD=CE
