人教版八年级数学下册课件:16.2二次根式的除法(2)(共27张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:16.2二次根式的除法(2)(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 808.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 11:12:12 | ||
图片预览



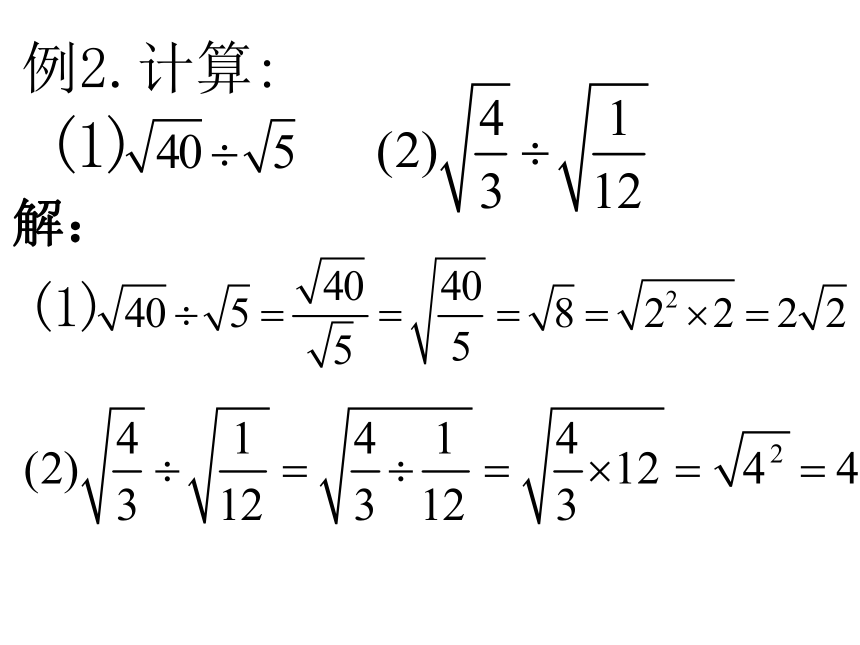
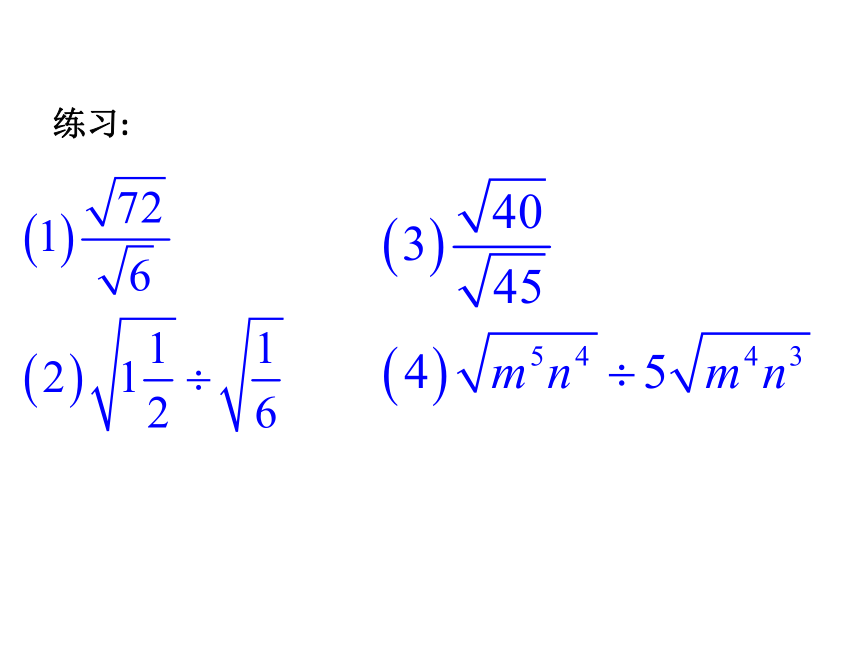



文档简介
二次根式除法法则:
两个二次根式相除,将它们的被开方数相除的商,作为商的被开方数;
解:
解:
练习:
小结:
二次根式性质4:
注意:(1)a、b的取值范围;
(2)当二次根式除以二次根式时的系数与系数相除,若二次根式前面有系数,可类比单项式除以单项式,即系数除系数,被开方数相除作被开方数。
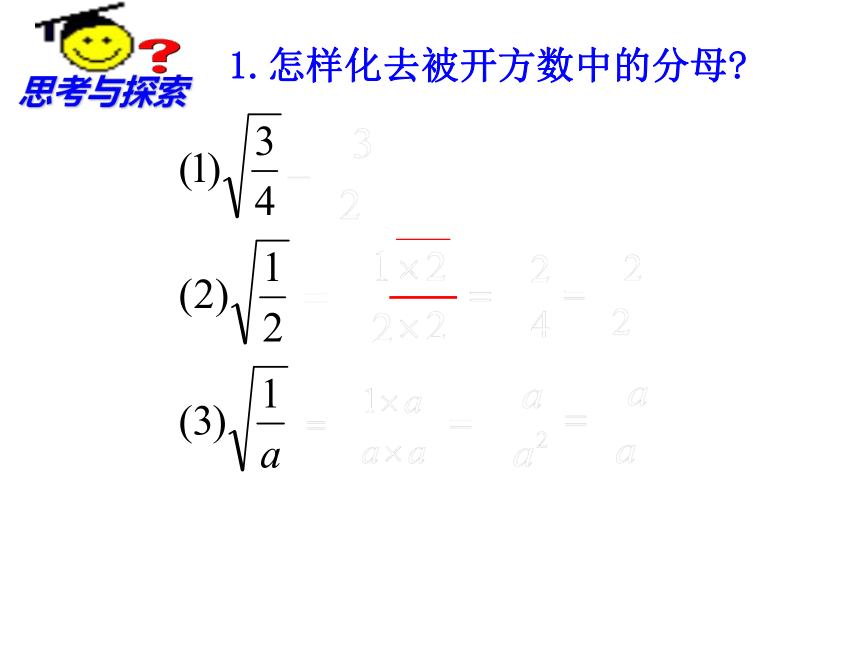
思考与探索
1.怎样化去被开方数中的分母?
由此你能的得到一般结论吗?
当a≥0,b>0时,怎样化去 中的分母?
由上面的计算可知:
二次根式的除法运算,通常采用分子、分母同乘以一个式子化去分母中的根号的方法,这种方法就叫做分母有理化
2.把下列各式分母有理化:
寻找分母的有理化因式,应找最简单的有理化因式,也可灵活运用我们学过的性质和法则,简化、优化解答过程。
化去根号中的分母:
解:(1)
(2)
(3)
化去分母中的根号:
解:(1)
(2)
(3)
化去分母中的根号:
尝试
交流
化去根号中的分母:
尝试
交流
化去分母中的根号:
一般地,二次根式运算的结果中,被开方数
中应
同样二次根式运算的结果中,被开方数中不
含分母、
例如:不能有象 ……
例如:不能有象 ……
分母中不含有根号.
不含能开得尽方的因数或因式.
最简二次根式
实际上就是使二次根式满足:
(1)被开方数中不含能开得尽方的因数或因式;
(2)被开方数中不含分母;
(3)分母中不含有根号.
像 不能作为二次根式的最后化简结果.
小结:
(a≥0,b>0)
利用它可以对二次根式进行化简.
探究
把 反过来,就可以得到:
例题讲解
化简:
解:
最简二次根式
1、被开方数不含分母(即被开方数的因数是整数,因式是整式);
2、被开方数中不含能开得尽方的因数或因式(即被开方数的每一个因数或因式的指数都小于2 )。
我们把满足上述两个条件的二次根式,
叫做最简二次根式。
二次根式的运算中,最后的结果中的二次根式一般要写成最简二次根式的形式。
下列根式中,哪些是最简二次根式?
探究
√
×
×
×
×
×
√
√
√
化简:
二次根式的化简要求满足以下两条:
(1)被开方数的因数是整数,因式是整式,也就是说“被开方数不含分母”.
(2)被开方数中不含能开得尽的因数或因式,也就是说“被开方数的每一个因数或因式的指数都小于2”.
判断下列各等式是否成立。
(1) ( )(2) ( )
(3) ( )(4) ( )
(5) ( )(6) ( )
×
×
×
√
辨析训练
√
√
注意点:
(1)当二次根式的被开方数中含有字母时应充分注意式子中所含字母的取值范围
(2)进行二次根式的乘除运算或化简,最终结果定要尽可能化简
2、计算:
两个二次根式相除,将它们的被开方数相除的商,作为商的被开方数;
解:
解:
练习:
小结:
二次根式性质4:
注意:(1)a、b的取值范围;
(2)当二次根式除以二次根式时的系数与系数相除,若二次根式前面有系数,可类比单项式除以单项式,即系数除系数,被开方数相除作被开方数。
思考与探索
1.怎样化去被开方数中的分母?
由此你能的得到一般结论吗?
当a≥0,b>0时,怎样化去 中的分母?
由上面的计算可知:
二次根式的除法运算,通常采用分子、分母同乘以一个式子化去分母中的根号的方法,这种方法就叫做分母有理化
2.把下列各式分母有理化:
寻找分母的有理化因式,应找最简单的有理化因式,也可灵活运用我们学过的性质和法则,简化、优化解答过程。
化去根号中的分母:
解:(1)
(2)
(3)
化去分母中的根号:
解:(1)
(2)
(3)
化去分母中的根号:
尝试
交流
化去根号中的分母:
尝试
交流
化去分母中的根号:
一般地,二次根式运算的结果中,被开方数
中应
同样二次根式运算的结果中,被开方数中不
含分母、
例如:不能有象 ……
例如:不能有象 ……
分母中不含有根号.
不含能开得尽方的因数或因式.
最简二次根式
实际上就是使二次根式满足:
(1)被开方数中不含能开得尽方的因数或因式;
(2)被开方数中不含分母;
(3)分母中不含有根号.
像 不能作为二次根式的最后化简结果.
小结:
(a≥0,b>0)
利用它可以对二次根式进行化简.
探究
把 反过来,就可以得到:
例题讲解
化简:
解:
最简二次根式
1、被开方数不含分母(即被开方数的因数是整数,因式是整式);
2、被开方数中不含能开得尽方的因数或因式(即被开方数的每一个因数或因式的指数都小于2 )。
我们把满足上述两个条件的二次根式,
叫做最简二次根式。
二次根式的运算中,最后的结果中的二次根式一般要写成最简二次根式的形式。
下列根式中,哪些是最简二次根式?
探究
√
×
×
×
×
×
√
√
√
化简:
二次根式的化简要求满足以下两条:
(1)被开方数的因数是整数,因式是整式,也就是说“被开方数不含分母”.
(2)被开方数中不含能开得尽的因数或因式,也就是说“被开方数的每一个因数或因式的指数都小于2”.
判断下列各等式是否成立。
(1) ( )(2) ( )
(3) ( )(4) ( )
(5) ( )(6) ( )
×
×
×
√
辨析训练
√
√
注意点:
(1)当二次根式的被开方数中含有字母时应充分注意式子中所含字母的取值范围
(2)进行二次根式的乘除运算或化简,最终结果定要尽可能化简
2、计算:
