人教版八年级数学下册课件:16.3二次根式的加减(3)课件(共31张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:16.3二次根式的加减(3)课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1006.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 00:00:00 | ||
图片预览











文档简介
(a≥0,b≥0)
(a≥0,b>0)
复习回顾
下列根式中,哪些是最简二次根式?
复习回顾
√
×
×
×
×
×
√
√
√
二次根式计算、化简的结果符合什么要求?
(1)被开方数不含分母;
分母不含根号;
(2)被开方数中不含能开得尽 方的因数或因式.
把下列各根式化简
下列3组根式各有什么特征?
几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
判断同类二次根式的关键是什么?
(1)化成最简二次根式,
(2)被开方数相同,根指数相同(都等于2)
必须先化成最简二次根式,再看被开方数是否相同,与最简二次根式前面的因式及符号无关.
如何判断几个二次根式是否为同类二次根式?
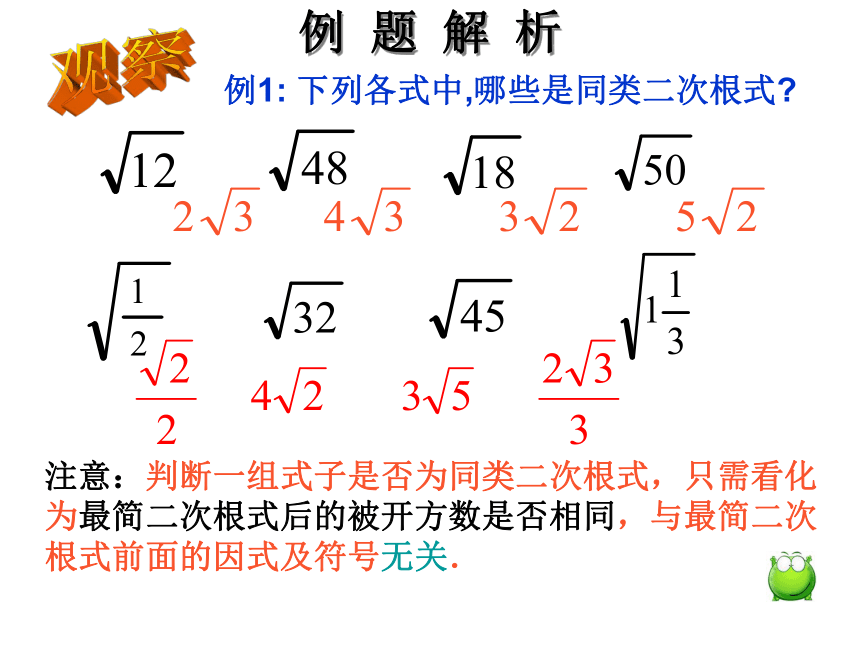
例1: 下列各式中,哪些是同类二次根式?
例 题 解 析
注意:判断一组式子是否为同类二次根式,只需看化为最简二次根式后的被开方数是否相同,与最简二次根式前面的因式及符号无关.
1.在下列各组根式中,是同类二次根式的是( )
A . B .
D.
3.如果最简二次根式 与 是同类二次根式,求m、n 的值.
B
125
2. 与 是同类二次根式的是( )
A. B. C. D.
D
同类二次根式合并:
把根号外系数或字母相加减,根指数和被开方数不变
注意:不是同类二次根式的二次根式
(如 与 )不能合并
下列各组二次根式哪些能合并?
练习
√
×
√
×
√
如何判断?
1、化简
2、比较被开方数
与合并同类项类似,把同类二次根式的系数相加减,做为结果的系数,根号及根号内部都不变,
2
9
=
(
)
2
4
3
2
+
+
=
2
4
2
3
2
2
+
+
=
2
4
18
8
+
+
总结二次根式加减运算的步骤
计算:
如何合并同类二次根式?
(3)合并同类二次根式。
一化
二找
三合并
二次根式加减法的步骤:
(1)将每个二次根式化为最简二次根式;
(2)找出其中的同类二次根式;
交流 归纳
注意:不是同类二次根式的二次根式
(如 与 )不能合并
1.判断:下列计算是否正确?为什么?
练习
F
F
T
判断:下列计算是否正确?为什么?
练习
F
F
F
解:
比较二次根式的加减与整式的加减,你能得出什么结论?
二次根式的加减实质是合并同类二次根式.
整式的加减的实质是合并同类项.
先化简,后合并
2.计算:
加减混合运算,应从左向右依次计算。
探究
解:原式=
别漏了“1”.
化简
如果结果中有分数,必须用假分数表示
解:原式=
运算不彻底,能合并的没有合并。
4.计算:
先化简,后合并
5.计算:
6
7.细心算一算
)
4
3
2
27
6
(
3
2
)
3
(
)
45
5
4
5
1
3
(
)
5
4
1
80
)(
2
(
)
72
3
2
50
8
1
1
(
)
25
.
0
2
8
)(
1
(
3
2
a
ab
a
b
ab
a
-
-
+
-
-
+
+
-
-
1.同类二次根式的定义?
2.二次根式加减运算的步骤?
3.如何合并同类二次根式?
合并同类二次根式与合并同类项类似.
小结
1.同类二次根式是相对于一组二次根式而言的.判断几个二次根式是否为同类二次根式,首先要把这几个二次根式化为最简二次根式,然后再看它们的被开方数,如果被开方数相同,那么原来的几个二次根式就是同类二次根式.
2.同类二次根式不一定是最简二次根式.如:
等.
3.几个二次根式相加减先把各个二次根式化成最简二次根式,再把同类二次根式分别合并.
(a≥0,b>0)
复习回顾
下列根式中,哪些是最简二次根式?
复习回顾
√
×
×
×
×
×
√
√
√
二次根式计算、化简的结果符合什么要求?
(1)被开方数不含分母;
分母不含根号;
(2)被开方数中不含能开得尽 方的因数或因式.
把下列各根式化简
下列3组根式各有什么特征?
几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
判断同类二次根式的关键是什么?
(1)化成最简二次根式,
(2)被开方数相同,根指数相同(都等于2)
必须先化成最简二次根式,再看被开方数是否相同,与最简二次根式前面的因式及符号无关.
如何判断几个二次根式是否为同类二次根式?
例1: 下列各式中,哪些是同类二次根式?
例 题 解 析
注意:判断一组式子是否为同类二次根式,只需看化为最简二次根式后的被开方数是否相同,与最简二次根式前面的因式及符号无关.
1.在下列各组根式中,是同类二次根式的是( )
A . B .
D.
3.如果最简二次根式 与 是同类二次根式,求m、n 的值.
B
125
2. 与 是同类二次根式的是( )
A. B. C. D.
D
同类二次根式合并:
把根号外系数或字母相加减,根指数和被开方数不变
注意:不是同类二次根式的二次根式
(如 与 )不能合并
下列各组二次根式哪些能合并?
练习
√
×
√
×
√
如何判断?
1、化简
2、比较被开方数
与合并同类项类似,把同类二次根式的系数相加减,做为结果的系数,根号及根号内部都不变,
2
9
=
(
)
2
4
3
2
+
+
=
2
4
2
3
2
2
+
+
=
2
4
18
8
+
+
总结二次根式加减运算的步骤
计算:
如何合并同类二次根式?
(3)合并同类二次根式。
一化
二找
三合并
二次根式加减法的步骤:
(1)将每个二次根式化为最简二次根式;
(2)找出其中的同类二次根式;
交流 归纳
注意:不是同类二次根式的二次根式
(如 与 )不能合并
1.判断:下列计算是否正确?为什么?
练习
F
F
T
判断:下列计算是否正确?为什么?
练习
F
F
F
解:
比较二次根式的加减与整式的加减,你能得出什么结论?
二次根式的加减实质是合并同类二次根式.
整式的加减的实质是合并同类项.
先化简,后合并
2.计算:
加减混合运算,应从左向右依次计算。
探究
解:原式=
别漏了“1”.
化简
如果结果中有分数,必须用假分数表示
解:原式=
运算不彻底,能合并的没有合并。
4.计算:
先化简,后合并
5.计算:
6
7.细心算一算
)
4
3
2
27
6
(
3
2
)
3
(
)
45
5
4
5
1
3
(
)
5
4
1
80
)(
2
(
)
72
3
2
50
8
1
1
(
)
25
.
0
2
8
)(
1
(
3
2
a
ab
a
b
ab
a
-
-
+
-
-
+
+
-
-
1.同类二次根式的定义?
2.二次根式加减运算的步骤?
3.如何合并同类二次根式?
合并同类二次根式与合并同类项类似.
小结
1.同类二次根式是相对于一组二次根式而言的.判断几个二次根式是否为同类二次根式,首先要把这几个二次根式化为最简二次根式,然后再看它们的被开方数,如果被开方数相同,那么原来的几个二次根式就是同类二次根式.
2.同类二次根式不一定是最简二次根式.如:
等.
3.几个二次根式相加减先把各个二次根式化成最简二次根式,再把同类二次根式分别合并.
