人教版八年级数学下册课件:19.1.1函数(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:19.1.1函数(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1008.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 11:22:38 | ||
图片预览






文档简介
(共18张PPT)
生活中处处都有物体的运动变化,如何从数学的角度来描述这些运动变化呢
欣赏图片
函数
列车从南京出发沿沪宁高速匀速驶向上海,列车在行驶的过程中,哪些量是没有变化的?哪些量是不断变化的?
自主探究
1、汽车行驶的速度
2、南京到上海两地总路程。
在某一变化过程中,数值保持不变的量叫常量。
1、汽车行驶的时间不断变化。
2、汽车行驶的路程不断变化。
3、汽车离上海的距离不断变化。
在变化过程中,可以取不同数值的量叫变量。
自主探究
不变的量:
变化的量:
注意:常量和变量不是绝对的,是对某一过程而言。
已知某水库的水位变化与蓄水量变化情况如下表所示:
水位/m 106 120 133 135 …
蓄水/m3 2.30×107 7.09×107 1.18×108 1.23×108 …
(1)你能从表格里获得哪些信息?有几个变量?
(2)水位高低与蓄水量是怎样变化的?
自 主 合 作
活动一
可以看出,随着水位升高,蓄水量增大;随着水位降低,蓄水量减少;当水位确定时,蓄水量也随着确定。
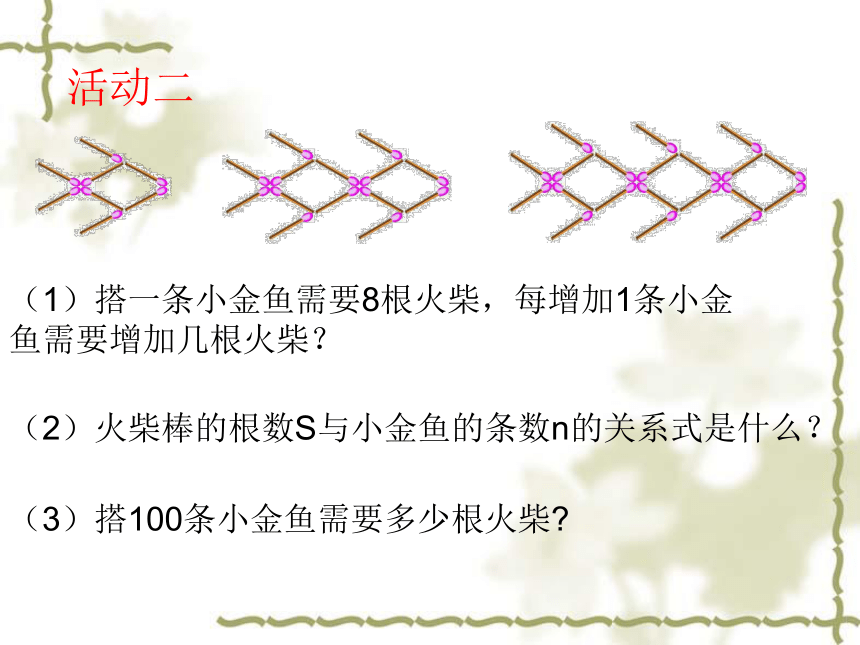
(1)搭一条小金鱼需要8根火柴,每增加1条小金鱼需要增加几根火柴?
(2)火柴棒的根数S与小金鱼的条数n的关系式是什么?
(3)搭100条小金鱼需要多少根火柴
活动二
随着 的
变化而变化,当 确定时,
也确定.
(4)根据小鱼的条数n与所需火柴棒的根数s的关系式,
可以看出:
火柴棒的根数S
小鱼的条数n
小鱼的条数n
火柴棒的根数S
在这个变化过程中,圆的面积与半径是怎样变化的?
活动 三
向平静的湖面投一石子,便会形成以落水点为圆心的一系列不断变化的圆。
可以看出,圆的 随着 的变化而变化,随着半径的确定而确定。
面积
半径
如图是某地一天内的气温变化图
(1)这天的6时、10时和14时的气温分别大约为多少度?
(2)这一天中,最高气温大约是多少度?最低气温大约是
多少度?
(3)图象中有几个变量?它们之间有怎样的关系?
·
·
活动四
上面的每个变化过程中有哪些共同之处?
在上述例子中,每个变化过程中都存在着两个变量,当其中一个变量变化时,另一个变量也随着发生变化,当一个变量确定时,另一个变量也随着确定。
1、水库水位变化与水库蓄水量变化而制作的表格.
2、搭小鱼的条数n和所需火柴根数S的关系式.
4、某一天内不同时刻气温变化图.
3、圆的面积和半径的关系式.
你还能举出几个类似的实例吗?
活动五
在每个变化过程中都存在着两个变量,当其中一个变量变化时,另一个变量也随着发生变化,当一个变量确定时,另一个变量也随着确定。
小组讨论交流
一般地,如果在 中 有 x和y,并且对于变量x的每 一个值,变量y都有 与它对应,那么我们称y是x的 。其中,x是 ,y是 。
一个变化的过程
两个变量
唯一的值
函数
自变量
因变量
注意:
1、有两个变量x和y。
2、因变量y的值随着自变量x的值的变化而变化。
3、自变量每确定一个值,因变量就有唯一确定的值与之对应。
温馨小提示:
这也是判断两个变量是否是函数关系的依据。
形成概念
例、用一根1m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为 m .
(2)当长方形的宽为0.2m时,长为 m .
(3)这个长方形的长是宽 的函数吗?为什么?
长方形的长y是宽x的函数.
理由:在这个变化过程中,有两个变量x和y,并且对于x的每一个值,y都有唯一的值与它对应.
0.8
0.9
自主交流
两个变量x、y满足关系式 ,填表并回答问题:
y是x的函数吗?为什么?
拓展提高
x 1 4 9 16
y
1.下表反映了y与x的关系,其中y是x的函数的是: .
y
12
15
y
y
x
x
1
3
5
2
4
.
×3
3
6
9
12
15
(1)
x
1
3
5
2
4
.
×3
3
6
9
12
15
(2)
1
3
5
2
4
.
×3
3
6
9
(3)
(1)
自 主 检 测
2、下列变量间的关系是不是函数关系 说明理由.
(1)长方形的宽是6,它的面积s与长a的关系。
(2)等腰三角形的底边长是8,它的周长y与腰长x的关系(x大于4)。
是函数关系
是函数关系
(3)在y=x2 +3 中,y是否是x的函数。
(4)在y2=x+3中,y是否是x的函数。
是函数关系
不是函数关系
自 主 检 测
这节课你有哪些收获?
课堂小结
一般地,如果在 中 有 x和y,并且对于变量x的每 一个值,变量y都有 与它对应,那么我们称y是x的 。其中,x是 ,y是 。
一个变化的过程
两个变量
唯一的值
函数
自变量
因变量
注意:
1、有两个变量x和y。
2、因变量y的值随自变量x的值的变化而变化。
3、自变量x每确定一个值,因变量y就有唯一确定的值与之对应。
巩固新知
生活中处处都有物体的运动变化,如何从数学的角度来描述这些运动变化呢
欣赏图片
函数
列车从南京出发沿沪宁高速匀速驶向上海,列车在行驶的过程中,哪些量是没有变化的?哪些量是不断变化的?
自主探究
1、汽车行驶的速度
2、南京到上海两地总路程。
在某一变化过程中,数值保持不变的量叫常量。
1、汽车行驶的时间不断变化。
2、汽车行驶的路程不断变化。
3、汽车离上海的距离不断变化。
在变化过程中,可以取不同数值的量叫变量。
自主探究
不变的量:
变化的量:
注意:常量和变量不是绝对的,是对某一过程而言。
已知某水库的水位变化与蓄水量变化情况如下表所示:
水位/m 106 120 133 135 …
蓄水/m3 2.30×107 7.09×107 1.18×108 1.23×108 …
(1)你能从表格里获得哪些信息?有几个变量?
(2)水位高低与蓄水量是怎样变化的?
自 主 合 作
活动一
可以看出,随着水位升高,蓄水量增大;随着水位降低,蓄水量减少;当水位确定时,蓄水量也随着确定。
(1)搭一条小金鱼需要8根火柴,每增加1条小金鱼需要增加几根火柴?
(2)火柴棒的根数S与小金鱼的条数n的关系式是什么?
(3)搭100条小金鱼需要多少根火柴
活动二
随着 的
变化而变化,当 确定时,
也确定.
(4)根据小鱼的条数n与所需火柴棒的根数s的关系式,
可以看出:
火柴棒的根数S
小鱼的条数n
小鱼的条数n
火柴棒的根数S
在这个变化过程中,圆的面积与半径是怎样变化的?
活动 三
向平静的湖面投一石子,便会形成以落水点为圆心的一系列不断变化的圆。
可以看出,圆的 随着 的变化而变化,随着半径的确定而确定。
面积
半径
如图是某地一天内的气温变化图
(1)这天的6时、10时和14时的气温分别大约为多少度?
(2)这一天中,最高气温大约是多少度?最低气温大约是
多少度?
(3)图象中有几个变量?它们之间有怎样的关系?
·
·
活动四
上面的每个变化过程中有哪些共同之处?
在上述例子中,每个变化过程中都存在着两个变量,当其中一个变量变化时,另一个变量也随着发生变化,当一个变量确定时,另一个变量也随着确定。
1、水库水位变化与水库蓄水量变化而制作的表格.
2、搭小鱼的条数n和所需火柴根数S的关系式.
4、某一天内不同时刻气温变化图.
3、圆的面积和半径的关系式.
你还能举出几个类似的实例吗?
活动五
在每个变化过程中都存在着两个变量,当其中一个变量变化时,另一个变量也随着发生变化,当一个变量确定时,另一个变量也随着确定。
小组讨论交流
一般地,如果在 中 有 x和y,并且对于变量x的每 一个值,变量y都有 与它对应,那么我们称y是x的 。其中,x是 ,y是 。
一个变化的过程
两个变量
唯一的值
函数
自变量
因变量
注意:
1、有两个变量x和y。
2、因变量y的值随着自变量x的值的变化而变化。
3、自变量每确定一个值,因变量就有唯一确定的值与之对应。
温馨小提示:
这也是判断两个变量是否是函数关系的依据。
形成概念
例、用一根1m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为 m .
(2)当长方形的宽为0.2m时,长为 m .
(3)这个长方形的长是宽 的函数吗?为什么?
长方形的长y是宽x的函数.
理由:在这个变化过程中,有两个变量x和y,并且对于x的每一个值,y都有唯一的值与它对应.
0.8
0.9
自主交流
两个变量x、y满足关系式 ,填表并回答问题:
y是x的函数吗?为什么?
拓展提高
x 1 4 9 16
y
1.下表反映了y与x的关系,其中y是x的函数的是: .
y
12
15
y
y
x
x
1
3
5
2
4
.
×3
3
6
9
12
15
(1)
x
1
3
5
2
4
.
×3
3
6
9
12
15
(2)
1
3
5
2
4
.
×3
3
6
9
(3)
(1)
自 主 检 测
2、下列变量间的关系是不是函数关系 说明理由.
(1)长方形的宽是6,它的面积s与长a的关系。
(2)等腰三角形的底边长是8,它的周长y与腰长x的关系(x大于4)。
是函数关系
是函数关系
(3)在y=x2 +3 中,y是否是x的函数。
(4)在y2=x+3中,y是否是x的函数。
是函数关系
不是函数关系
自 主 检 测
这节课你有哪些收获?
课堂小结
一般地,如果在 中 有 x和y,并且对于变量x的每 一个值,变量y都有 与它对应,那么我们称y是x的 。其中,x是 ,y是 。
一个变化的过程
两个变量
唯一的值
函数
自变量
因变量
注意:
1、有两个变量x和y。
2、因变量y的值随自变量x的值的变化而变化。
3、自变量x每确定一个值,因变量y就有唯一确定的值与之对应。
巩固新知
