人教版初中数学八年级下册17.2.3《勾股定理及其逆定理的综合应用》课件(共16张PPT)
文档属性
| 名称 | 人教版初中数学八年级下册17.2.3《勾股定理及其逆定理的综合应用》课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 469.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 11:28:39 | ||
图片预览




文档简介
勾股定理
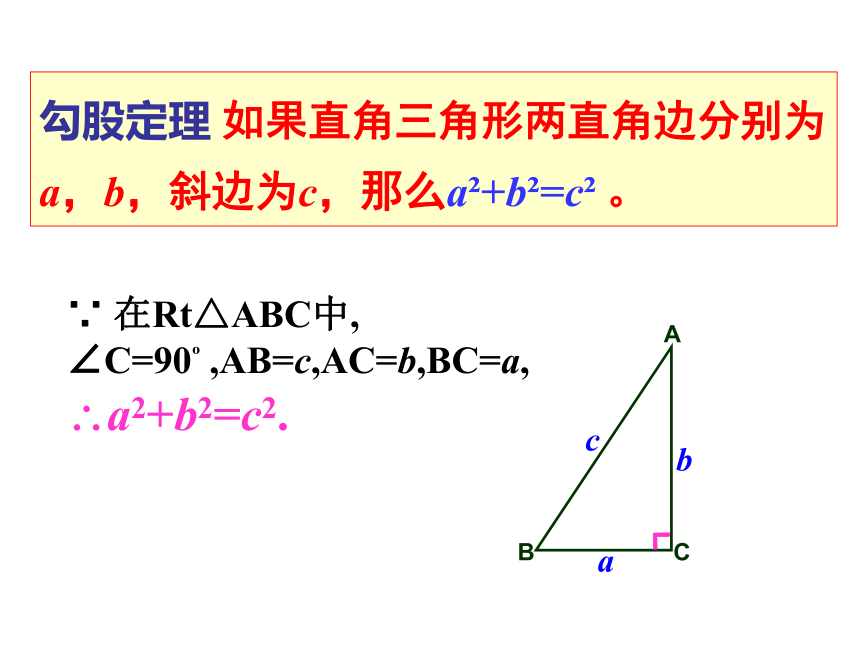
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a?+b?=c? 。
c
a
b
A
B
C
∵ 在Rt△ABC中, ∠C=90? ,AB=c,AC=b,BC=a,
?a2+b2=c2.
┏
(2)已知:直角△ABC中,∠C=90°
若a=8,c=17,则b=__。
(3)已知:直角△ABC中,∠C=90°
若a:b=3:4,c=10cm,则a=__,b=__。
c
a
b
A
B
C
┏
8
6
15
13
小试身手
口答:
(1)已知:直角△ABC中,∠C=90°,
若a=5,b=12,则c=__。
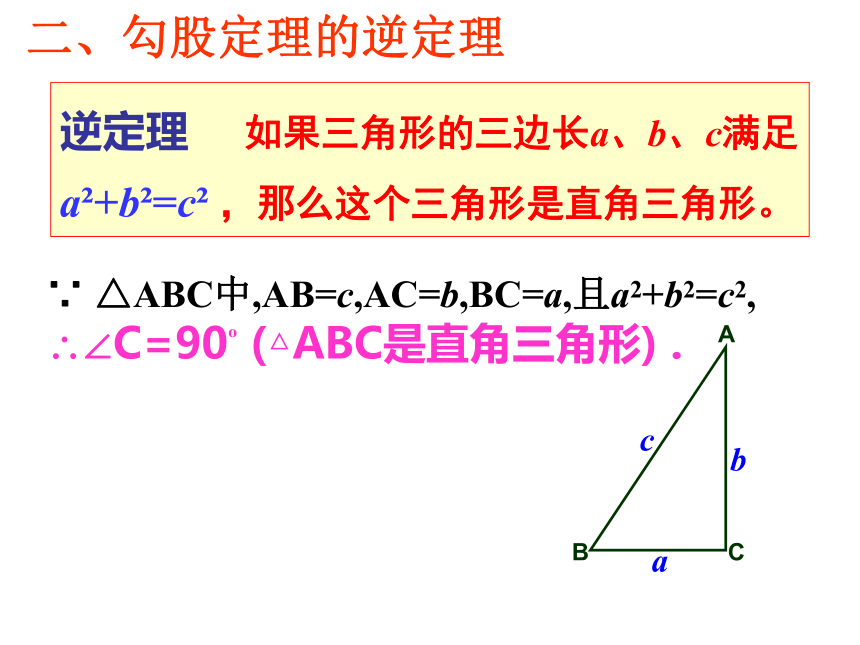
逆定理 如果三角形的三边长a、b、c满足a?+b?=c? ,那么这个三角形是直角三角形。
∵ △ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,
?∠C=90? (△ABC是直角三角形) .
c
a
b
A
B
C
二、勾股定理的逆定理
小试身手
1、以下各组为边长,能构成直角三角形的( )
A
C
2﹑三角形的三边长a﹑b﹑c,满足
,则这个三角形是 ( )
A.等边三角形 B.钝角三角形
C.直角三角形 D.锐角三角形
A.
B.
C. 9, 16, 25 D. 1, 2, 3
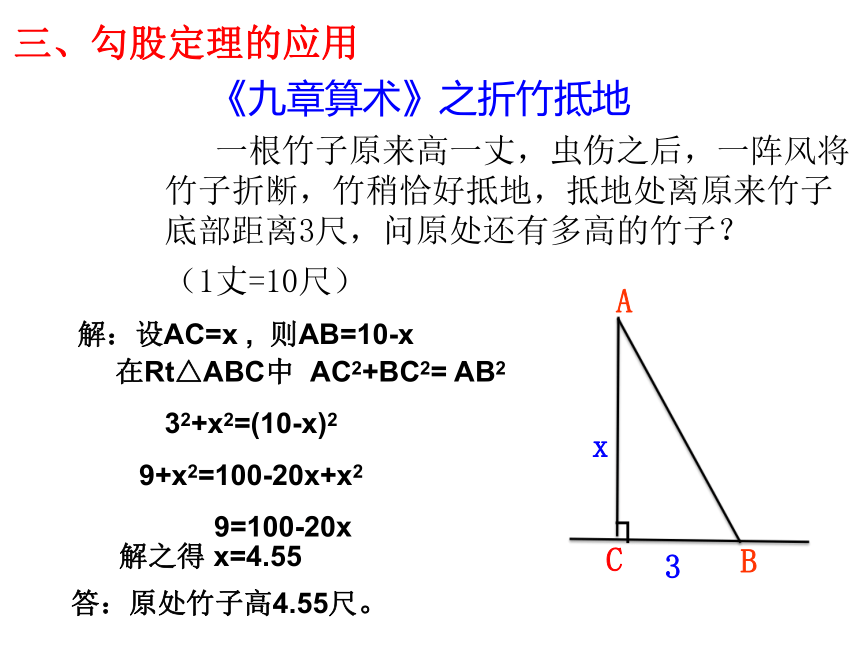
《九章算术》之折竹抵地
一根竹子原来高一丈,虫伤之后,一阵风将 竹子折断,竹稍恰好抵地,抵地处离原来竹子底部距离3尺,问原处还有多高的竹子?
(1丈=10尺)
┐
A
B
C
3
x
解:设AC=x , 则AB=10-x
在Rt△ABC中 AC2+BC2= AB2
32+x2=(10-x)2
9+x2=100-20x+x2
9=100-20x
答:原处竹子高4.55尺。
解之得 x=4.55
三、勾股定理的应用
最短路程问题
例1:如图所示,有一个高为12cm,底面周长为32cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米?
A
B
展开
yuanzhu-zhankai.gsp
A
B
c
解:如图,在Rt△ABC中,BC=底面周长的一半=32÷2=16, AC=12
答:最短路程为20cm。
AB=
112
A
C
B
拓展1:如果圆柱换成如图的棱长10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
A
10
10
10
B
C
A
解:在Rt△ABC中,AC=20,BC=10
答:最短路径是 cm.
B
A
展开izhengfangti-zhankaitu.gsp
拓展2:如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1行的路线最短.
A
B
A1
B1
D
C
D1
C1
2
1
4
4
1
2
B
C 1
D
C
①
D1
A
②
A
B
B1
C
A1
C1
4
1
2
A
B
A1
B1
D
C
D1
C1
2
1
4
③
A
C1
B1
A1
D1
D
1
2
4
②
A
A1
C1
③
B1
D1
D
4
1
2
D
C
4
A
B
D1
C1
①
2
1
A
B
B1
C
A1
C1
4
1
2
A
B
A1
B1
D
C
D1
C1
2
1
4
答:最短路程是5.
1.如图,在四边形ABCD中,∠B= ,AB=3,BC=4,CD=13,AD=12,求四边形ABCD的面积。
A
B
D
C
90?
解:连接AC,
在△ACD中,
即AC2+AD2=CD2
所以△ACD是直角三角形
则S 四边形ABCD=S △ABC+S △ACD
AC=
在Rt△ABC中,AB=3,BC=4
132=169
因为52+122=169
= × 6×4 + ×12×5
= 6+30=36
┐
3
4
13
12
答:四边形的面积是36.
定理的综合运用
1﹑在直角三角形中,若知道三角形的任意两条边,直接根据勾股定理求出第三边,有时用到方程的思想。
2 ﹑若没有出现直角三角形,先构造出直角三角形,再运用勾股定理。
3﹑在立体图形中,先展开成平面图形,出现直角三角形,再运用勾股定理。
五:小结
《九章算术》之枯树缠藤
一棵高2丈的枯树直立在地上,粗3尺,有一根藤条从树根处缠绕而上,缠绕7周到达树顶,请问这根藤条有多长?
(1丈=10尺)
思考
五:作业
见
补充题见学案
勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a?+b?=c? 。
c
a
b
A
B
C
∵ 在Rt△ABC中, ∠C=90? ,AB=c,AC=b,BC=a,
?a2+b2=c2.
┏
(2)已知:直角△ABC中,∠C=90°
若a=8,c=17,则b=__。
(3)已知:直角△ABC中,∠C=90°
若a:b=3:4,c=10cm,则a=__,b=__。
c
a
b
A
B
C
┏
8
6
15
13
小试身手
口答:
(1)已知:直角△ABC中,∠C=90°,
若a=5,b=12,则c=__。
逆定理 如果三角形的三边长a、b、c满足a?+b?=c? ,那么这个三角形是直角三角形。
∵ △ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,
?∠C=90? (△ABC是直角三角形) .
c
a
b
A
B
C
二、勾股定理的逆定理
小试身手
1、以下各组为边长,能构成直角三角形的( )
A
C
2﹑三角形的三边长a﹑b﹑c,满足
,则这个三角形是 ( )
A.等边三角形 B.钝角三角形
C.直角三角形 D.锐角三角形
A.
B.
C. 9, 16, 25 D. 1, 2, 3
《九章算术》之折竹抵地
一根竹子原来高一丈,虫伤之后,一阵风将 竹子折断,竹稍恰好抵地,抵地处离原来竹子底部距离3尺,问原处还有多高的竹子?
(1丈=10尺)
┐
A
B
C
3
x
解:设AC=x , 则AB=10-x
在Rt△ABC中 AC2+BC2= AB2
32+x2=(10-x)2
9+x2=100-20x+x2
9=100-20x
答:原处竹子高4.55尺。
解之得 x=4.55
三、勾股定理的应用
最短路程问题
例1:如图所示,有一个高为12cm,底面周长为32cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米?
A
B
展开
yuanzhu-zhankai.gsp
A
B
c
解:如图,在Rt△ABC中,BC=底面周长的一半=32÷2=16, AC=12
答:最短路程为20cm。
AB=
112
A
C
B
拓展1:如果圆柱换成如图的棱长10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
A
10
10
10
B
C
A
解:在Rt△ABC中,AC=20,BC=10
答:最短路径是 cm.
B
A
展开izhengfangti-zhankaitu.gsp
拓展2:如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1行的路线最短.
A
B
A1
B1
D
C
D1
C1
2
1
4
4
1
2
B
C 1
D
C
①
D1
A
②
A
B
B1
C
A1
C1
4
1
2
A
B
A1
B1
D
C
D1
C1
2
1
4
③
A
C1
B1
A1
D1
D
1
2
4
②
A
A1
C1
③
B1
D1
D
4
1
2
D
C
4
A
B
D1
C1
①
2
1
A
B
B1
C
A1
C1
4
1
2
A
B
A1
B1
D
C
D1
C1
2
1
4
答:最短路程是5.
1.如图,在四边形ABCD中,∠B= ,AB=3,BC=4,CD=13,AD=12,求四边形ABCD的面积。
A
B
D
C
90?
解:连接AC,
在△ACD中,
即AC2+AD2=CD2
所以△ACD是直角三角形
则S 四边形ABCD=S △ABC+S △ACD
AC=
在Rt△ABC中,AB=3,BC=4
132=169
因为52+122=169
= × 6×4 + ×12×5
= 6+30=36
┐
3
4
13
12
答:四边形的面积是36.
定理的综合运用
1﹑在直角三角形中,若知道三角形的任意两条边,直接根据勾股定理求出第三边,有时用到方程的思想。
2 ﹑若没有出现直角三角形,先构造出直角三角形,再运用勾股定理。
3﹑在立体图形中,先展开成平面图形,出现直角三角形,再运用勾股定理。
五:小结
《九章算术》之枯树缠藤
一棵高2丈的枯树直立在地上,粗3尺,有一根藤条从树根处缠绕而上,缠绕7周到达树顶,请问这根藤条有多长?
(1丈=10尺)
思考
五:作业
见
补充题见学案
