人教版初中数学七年级下册6.1.1算术平方根课件(共24张PPT)
文档属性
| 名称 | 人教版初中数学七年级下册6.1.1算术平方根课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 17:31:50 | ||
图片预览








文档简介
6.1.1算术平方根
第六章 实数
课程要求
1、知道什么叫做算术平方根,会表示及读出一个非负数的算术平方根;
2、理解平方和求算术平方根是互逆过程,利用平方计算一个非负数的算术平方根。
探索
问题:黄岗初中要举行美术作品比赛,叶慧燕很高兴,她想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
因为 52=25, 所以 边长为5dm.
你会求吗?
正方形的面积
1
9
16
36
0.25
边长
1
3
4
6
0.5
这个问题实际上是已知一个正数的平方,求这个正数的问题。
探索
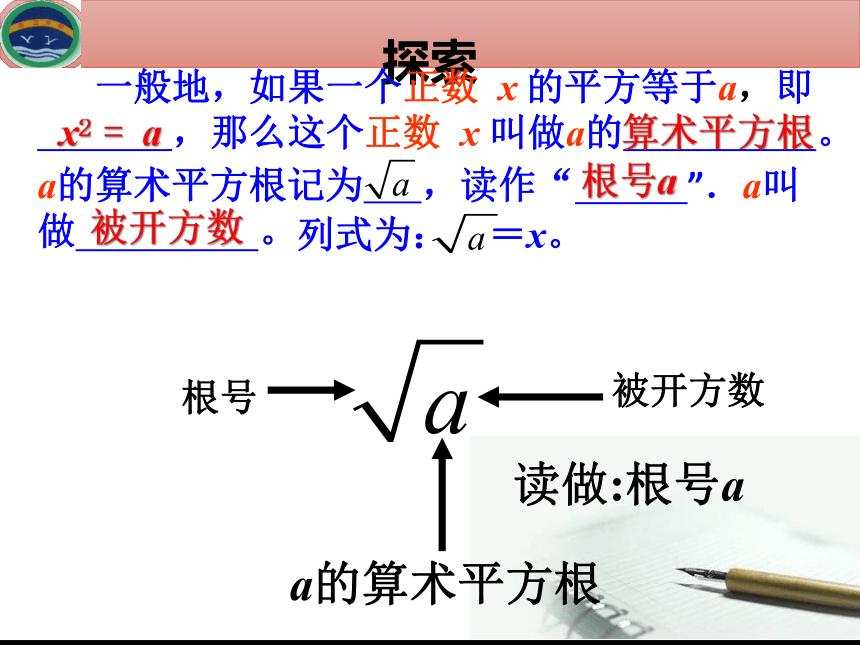
a的算术平方根记为 ,读作“ ”.a叫做 。
一般地,如果一个正数 x 的平方等于a,即
,那么这个正数 x 叫做a的 。
列式为: =x。
x2 = a
算术平方根
根号a
被开方数
根号
被开方数
读做:根号a
a的算术平方根
探索
应用举例:因为52=25,那么根据定义,5就是25的算术平方根。即 .
特别提醒:
1.0 的算术平方根是 ;
0
2. 正数有 个算术平方根,负数 算术平方根;
一
没有
3. 是个运算符号,它表示求一个数的算术平方根;
4. 的意义: a的算术平方根,且 a ≥0, ≥0。
的 双重非负性
1. a ≥0
2. ≥0
例题
例1、9的算术平方根是 ,4的算术平方根是 ,2的算术平方根是 。
例2、求下列各数的算术平方根。
(1)100; (2) ; (3) 0.0001;
(4) ; (5)1.21;
3
2
解:(1)∵102=100,∴
结论:被开方数越大,对应的算术平方根也越大。
例题
例3、你知道下列式子表示什么意思吗? 你能求出它们的值吗?
(1) ;(2) ;(3) ;(4) 。
解:(1)表示1的算术平方根,
(2)表示
的算术平方根,
(3)表示
的算术平方根,
(4)表示(
的算术平方根,
例题
例4、(3+a)的算术平方根是5,求a的值。
a=22
解:
课堂检测
1、下列命题中,正确的个数有( )
①1的算术平方根是1;②(-1)2的算术平方根是-1;③一个数的算术平方根等于它本身,这个数只能是零;④-4没有算术平方根。
A.1个; B.2个; C.3个; D.4个。
2、一个自然数的算术平方根是x,则下一个自然数的算术平方根是( )
A. +1; B. C. D.x+1
B
C
课堂检测
3、x是16的算术平方根,则x的算术平方根是( )
A.4; B.2; C. ; D.±4。
4、若 ,则x的算术平方根是( )
A. 49; B. 53; C.7; D.
6、36的算术平方根是_____。
7、算术平方根等于它本身的数是_______。
8、 = ;- = ;
± = ; = 。
9、 的算术平方根是________。
10、若 + 有意义,则a为________。
B
D
6
0和1
6
-7
±5
a(a≥0)或—a(a≤0)
1
课堂检测
2
0.8
1
2
课堂检测
13、若 =2,求2x+5的算术平方根.
课堂检测
14、已知a为 的整数部分,b-1是400的算术平方根,求
.
.
课堂小结
1.今天你有什么收获?
2.完成一课一练相关练习。
探究
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?
小正方形的对角线的长是多少呢?
如图,把两个小正方形沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2的大正方形。你知道这个大正方形的边长是多少吗?
设大正方形的边长为x,则
=2.
由算术平方根的意义可知
x=
.
你知道 有多大吗?
无限不循环小数
逼近法
无理数
方法应用
.
判断 在哪两个相邻整数的范围之间。
练习:估计出与 最接近的两个整数。
∵9<13<16
探究
.
小丽想用一块面积为400cm2正方形纸片,沿着边的方向裁出一块面积为300cm2的长方形纸片用来绘画,使它的长宽之比为3:2,不知能否裁出来,正在发愁。小明见了说
“别发愁,一定能用
一块面积大的纸片裁
出一块面积小的纸片”,
你同意小明的说法吗?
小丽能用这块纸片裁
出符合要求的纸片吗?
探究
.
即长方形纸片的长应该大于21cm
答:不能同意小明的说法,小丽不能用这块正方形纸片裁出符合要求的长方形纸片.
例题
.
试比较下列各组数的大小
(2)
<
<
课堂检测
.
练习:比较 与12的大小?
课堂检测
.
比较 与12的大小。
估计与 最接近的两个整数分别是多少。
第六章 实数
课程要求
1、知道什么叫做算术平方根,会表示及读出一个非负数的算术平方根;
2、理解平方和求算术平方根是互逆过程,利用平方计算一个非负数的算术平方根。
探索
问题:黄岗初中要举行美术作品比赛,叶慧燕很高兴,她想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
因为 52=25, 所以 边长为5dm.
你会求吗?
正方形的面积
1
9
16
36
0.25
边长
1
3
4
6
0.5
这个问题实际上是已知一个正数的平方,求这个正数的问题。
探索
a的算术平方根记为 ,读作“ ”.a叫做 。
一般地,如果一个正数 x 的平方等于a,即
,那么这个正数 x 叫做a的 。
列式为: =x。
x2 = a
算术平方根
根号a
被开方数
根号
被开方数
读做:根号a
a的算术平方根
探索
应用举例:因为52=25,那么根据定义,5就是25的算术平方根。即 .
特别提醒:
1.0 的算术平方根是 ;
0
2. 正数有 个算术平方根,负数 算术平方根;
一
没有
3. 是个运算符号,它表示求一个数的算术平方根;
4. 的意义: a的算术平方根,且 a ≥0, ≥0。
的 双重非负性
1. a ≥0
2. ≥0
例题
例1、9的算术平方根是 ,4的算术平方根是 ,2的算术平方根是 。
例2、求下列各数的算术平方根。
(1)100; (2) ; (3) 0.0001;
(4) ; (5)1.21;
3
2
解:(1)∵102=100,∴
结论:被开方数越大,对应的算术平方根也越大。
例题
例3、你知道下列式子表示什么意思吗? 你能求出它们的值吗?
(1) ;(2) ;(3) ;(4) 。
解:(1)表示1的算术平方根,
(2)表示
的算术平方根,
(3)表示
的算术平方根,
(4)表示(
的算术平方根,
例题
例4、(3+a)的算术平方根是5,求a的值。
a=22
解:
课堂检测
1、下列命题中,正确的个数有( )
①1的算术平方根是1;②(-1)2的算术平方根是-1;③一个数的算术平方根等于它本身,这个数只能是零;④-4没有算术平方根。
A.1个; B.2个; C.3个; D.4个。
2、一个自然数的算术平方根是x,则下一个自然数的算术平方根是( )
A. +1; B. C. D.x+1
B
C
课堂检测
3、x是16的算术平方根,则x的算术平方根是( )
A.4; B.2; C. ; D.±4。
4、若 ,则x的算术平方根是( )
A. 49; B. 53; C.7; D.
6、36的算术平方根是_____。
7、算术平方根等于它本身的数是_______。
8、 = ;- = ;
± = ; = 。
9、 的算术平方根是________。
10、若 + 有意义,则a为________。
B
D
6
0和1
6
-7
±5
a(a≥0)或—a(a≤0)
1
课堂检测
2
0.8
1
2
课堂检测
13、若 =2,求2x+5的算术平方根.
课堂检测
14、已知a为 的整数部分,b-1是400的算术平方根,求
.
.
课堂小结
1.今天你有什么收获?
2.完成一课一练相关练习。
探究
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?
小正方形的对角线的长是多少呢?
如图,把两个小正方形沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2的大正方形。你知道这个大正方形的边长是多少吗?
设大正方形的边长为x,则
=2.
由算术平方根的意义可知
x=
.
你知道 有多大吗?
无限不循环小数
逼近法
无理数
方法应用
.
判断 在哪两个相邻整数的范围之间。
练习:估计出与 最接近的两个整数。
∵9<13<16
探究
.
小丽想用一块面积为400cm2正方形纸片,沿着边的方向裁出一块面积为300cm2的长方形纸片用来绘画,使它的长宽之比为3:2,不知能否裁出来,正在发愁。小明见了说
“别发愁,一定能用
一块面积大的纸片裁
出一块面积小的纸片”,
你同意小明的说法吗?
小丽能用这块纸片裁
出符合要求的纸片吗?
探究
.
即长方形纸片的长应该大于21cm
答:不能同意小明的说法,小丽不能用这块正方形纸片裁出符合要求的长方形纸片.
例题
.
试比较下列各组数的大小
(2)
<
<
课堂检测
.
练习:比较 与12的大小?
课堂检测
.
比较 与12的大小。
估计与 最接近的两个整数分别是多少。
