人教版初中数学七年级下册6.2.1《立方根的概念》课件(共21张PPT)
文档属性
| 名称 | 人教版初中数学七年级下册6.2.1《立方根的概念》课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 17:33:01 | ||
图片预览






文档简介
复 习
1)
2)
正数a的平方根是:
正数a的算术平方根是:
3)
0的平方根是:
0的算术平方根是:
0
0
1.平方根的定义?
2.我们把求平方根的运算称之为
开平方
开平方运算与乘方运算是
互逆运算
学习目标:
(1)了解立方根的概念.
(2)会求一些数的立方根.
学习重点:
类比平方根学习立方根的概念和求法.
设这种包装箱的棱长为xm,则x3=27
这就是要求一个数,使它的的立方等于27.
因为 33=27
所以 x=3,
即这种包装箱的棱长应为3m.
问题 要制作一种容积为27m3的正方体的
包装箱,这种包装箱的棱长应该是多少?
什么是立方根?
一般的,如果一个数的 等
于a,那么这个数叫做a的
或者 。 这就是说,如
果 ,那么x叫做a的 。
平方
平方根
二次方根
平方根
x2=a
立方
立方根
三次方根
立方根
x3=a
什么叫做数a的 ?
回忆
平方根
立方根
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.记作 .
3
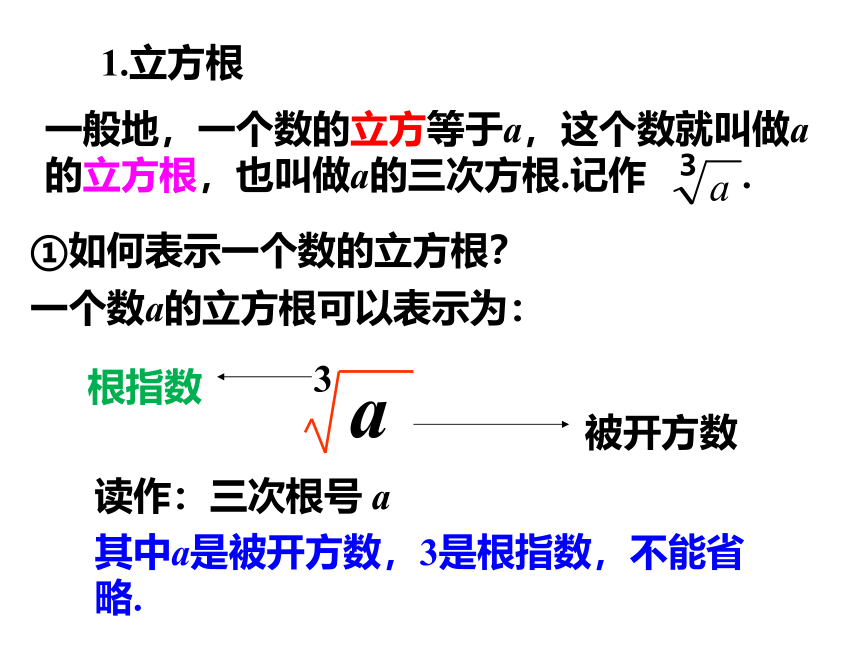
1.立方根
①如何表示一个数的立方根?
一个数a的立方根可以表示为:
a
3
根指数
被开方数
其中a是被开方数,3是根指数,不能省略.
读作:三次根号 a
牛刀小试
写出下列各数的立方根
(1) 4
(2)-9
(3)
(4)
a
3
a的立方根是
( )3=1 ( )3=8 ( )3=
( )3=0 ( )3=-64
数a
1
2
1
a的立方根
8
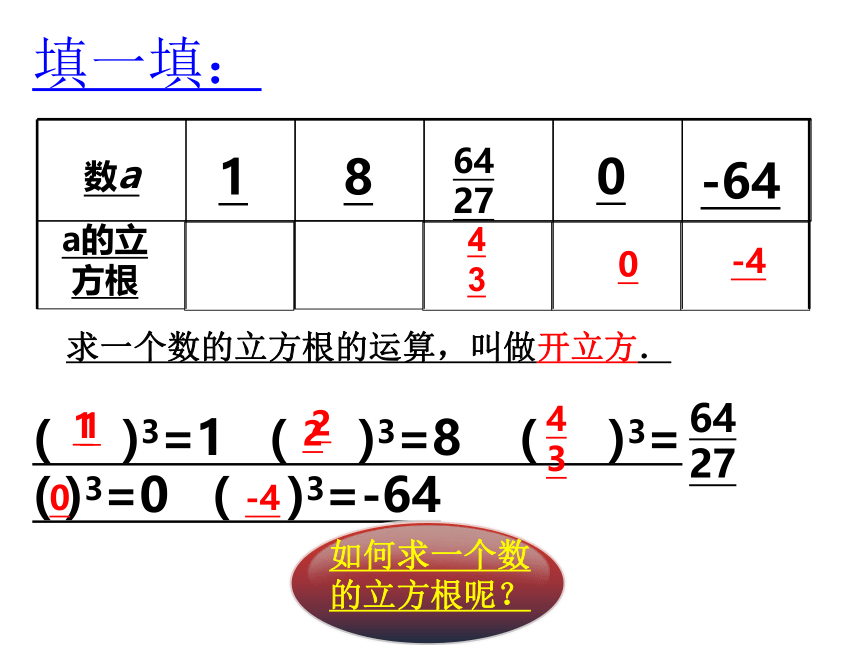
填一填:
0
-64
64
27
64
27
如何求一个数的立方根呢?
求一个数的立方根的运算,叫做开立方.
0
-4
0
-4
1
2
4
3
4
3
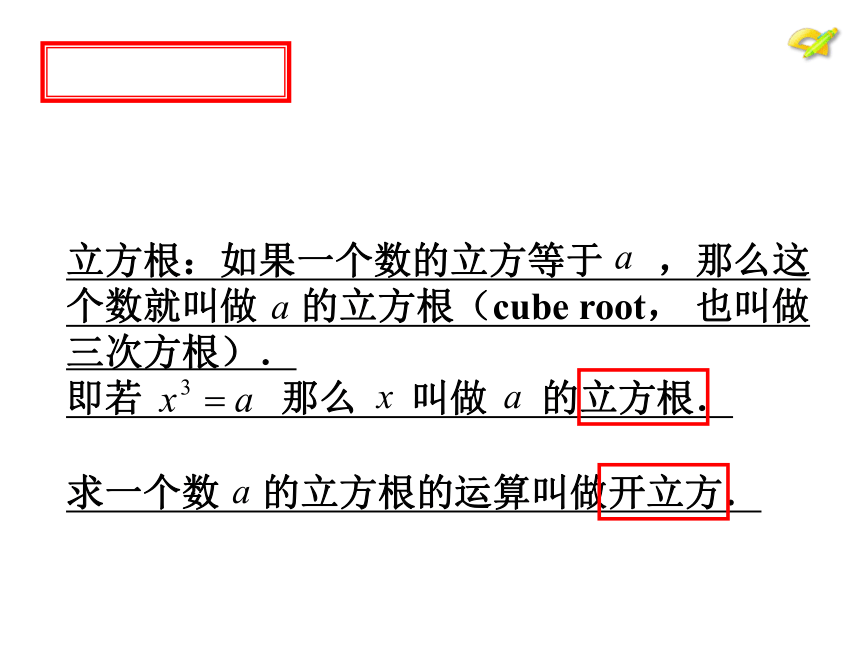
立方根:如果一个数的立方等于 ,那么这个数就叫做 的立方根(cube root, 也叫做三次方根).
即若 那么 叫做 的立方根.
求一个数 的立方根的运算叫做开立方.
②求一个数的立方根的运算,叫做开立方
立方
开立方
互逆
到现在我们学了几种运算?
+,-,x,÷,乘方,开方(开平方,开立方)
根据立方根的意义填空.你能发现正数、0和负数的立方根各有什么特点吗?
2.探究立方根的性质
因为 ,所以8的立方根是( );
因为 ,所以0.064的立方根是( );
因为 ,所以0的立方根是( );
因为 ,所以-8的立方根是( );
因为 ,所以 的立方根是( ).
因为( 0.4 ) =0.064,所以0.064的立方跟 根是(0.4 )
2.立方根的性质
探究1. 根据立方根的意义填空.
因为 =8,所以8的立方根是( )
因为( ) =0,所以0的立方根是( )
因为 ( ) =-8,所以-8的立方根是( )
因为( ) =- ,所以- 的立方根是( )
0
2
-2
0
-2
3
2
-
3
2
-
你能看出正数,0,负数的立方根各有什么特点?
正数有立方根吗?如果有,有几个?
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
立方根的性质
讨论:你能归纳出平方根和立方根的异同点吗?
被开方数
平方根
立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
练一练
1.判断下列说法是否正确,并说明理由
x
(2) 25的平方根是5
x
(3) -216没有立方根
x
(4) -4的平方根是
x
(5) 0的平方根和立方根都是0
√
(1)
的立方根是
例1 求下列各数的立方根
(1) 27 (2)-27 (3) (4)-0.064
解:
(1)∵
∴27的立方根是3
即
(2)∵
∴-27的立方根是-3
即
(4)
∴-0.064的立方根是-0.4
∵
(3)∵
3
∴ 的立方根是
3
1
巩固练习
1、求下列各数的立方根
2、 下列各式中,正确的是( )
(1)-216; (2)0.008;
(3)-106; (4)
- 6
0.2
- 102
C
3、 下列说法正确的是:( )
(A)如果一个数的立方根是这个数本身,那么这个数一定是零。
(B)一个数的立方根与这个数同号,且零的立方根是零。
(C)1的立方根是±1。
(D)负数没有立方根。
B
4、判 断
(1)5是125的立方根 ( )
(2)-27的立方根是3 ( )
(3) =±4 ( )
(4)-5是-125的立方根 ( )
5. 求下列式子中x的值。
√
×
×
√
课堂小结
相同点:①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果.
不同点:①定义不同
②个数不同
③表示方法不同
④被开方数的取值范围不同
1.立方根的定义,性质,计算.
2.立方根与平方根的异同
课后作业
1.布置作业:从教材“习题6.2”中
1、2、 3、5.
2.完成同步测评练习册中本课时的习题.
1)
2)
正数a的平方根是:
正数a的算术平方根是:
3)
0的平方根是:
0的算术平方根是:
0
0
1.平方根的定义?
2.我们把求平方根的运算称之为
开平方
开平方运算与乘方运算是
互逆运算
学习目标:
(1)了解立方根的概念.
(2)会求一些数的立方根.
学习重点:
类比平方根学习立方根的概念和求法.
设这种包装箱的棱长为xm,则x3=27
这就是要求一个数,使它的的立方等于27.
因为 33=27
所以 x=3,
即这种包装箱的棱长应为3m.
问题 要制作一种容积为27m3的正方体的
包装箱,这种包装箱的棱长应该是多少?
什么是立方根?
一般的,如果一个数的 等
于a,那么这个数叫做a的
或者 。 这就是说,如
果 ,那么x叫做a的 。
平方
平方根
二次方根
平方根
x2=a
立方
立方根
三次方根
立方根
x3=a
什么叫做数a的 ?
回忆
平方根
立方根
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.记作 .
3
1.立方根
①如何表示一个数的立方根?
一个数a的立方根可以表示为:
a
3
根指数
被开方数
其中a是被开方数,3是根指数,不能省略.
读作:三次根号 a
牛刀小试
写出下列各数的立方根
(1) 4
(2)-9
(3)
(4)
a
3
a的立方根是
( )3=1 ( )3=8 ( )3=
( )3=0 ( )3=-64
数a
1
2
1
a的立方根
8
填一填:
0
-64
64
27
64
27
如何求一个数的立方根呢?
求一个数的立方根的运算,叫做开立方.
0
-4
0
-4
1
2
4
3
4
3
立方根:如果一个数的立方等于 ,那么这个数就叫做 的立方根(cube root, 也叫做三次方根).
即若 那么 叫做 的立方根.
求一个数 的立方根的运算叫做开立方.
②求一个数的立方根的运算,叫做开立方
立方
开立方
互逆
到现在我们学了几种运算?
+,-,x,÷,乘方,开方(开平方,开立方)
根据立方根的意义填空.你能发现正数、0和负数的立方根各有什么特点吗?
2.探究立方根的性质
因为 ,所以8的立方根是( );
因为 ,所以0.064的立方根是( );
因为 ,所以0的立方根是( );
因为 ,所以-8的立方根是( );
因为 ,所以 的立方根是( ).
因为( 0.4 ) =0.064,所以0.064的立方跟 根是(0.4 )
2.立方根的性质
探究1. 根据立方根的意义填空.
因为 =8,所以8的立方根是( )
因为( ) =0,所以0的立方根是( )
因为 ( ) =-8,所以-8的立方根是( )
因为( ) =- ,所以- 的立方根是( )
0
2
-2
0
-2
3
2
-
3
2
-
你能看出正数,0,负数的立方根各有什么特点?
正数有立方根吗?如果有,有几个?
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零.
立方根的性质
讨论:你能归纳出平方根和立方根的异同点吗?
被开方数
平方根
立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
练一练
1.判断下列说法是否正确,并说明理由
x
(2) 25的平方根是5
x
(3) -216没有立方根
x
(4) -4的平方根是
x
(5) 0的平方根和立方根都是0
√
(1)
的立方根是
例1 求下列各数的立方根
(1) 27 (2)-27 (3) (4)-0.064
解:
(1)∵
∴27的立方根是3
即
(2)∵
∴-27的立方根是-3
即
(4)
∴-0.064的立方根是-0.4
∵
(3)∵
3
∴ 的立方根是
3
1
巩固练习
1、求下列各数的立方根
2、 下列各式中,正确的是( )
(1)-216; (2)0.008;
(3)-106; (4)
- 6
0.2
- 102
C
3、 下列说法正确的是:( )
(A)如果一个数的立方根是这个数本身,那么这个数一定是零。
(B)一个数的立方根与这个数同号,且零的立方根是零。
(C)1的立方根是±1。
(D)负数没有立方根。
B
4、判 断
(1)5是125的立方根 ( )
(2)-27的立方根是3 ( )
(3) =±4 ( )
(4)-5是-125的立方根 ( )
5. 求下列式子中x的值。
√
×
×
√
课堂小结
相同点:①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果.
不同点:①定义不同
②个数不同
③表示方法不同
④被开方数的取值范围不同
1.立方根的定义,性质,计算.
2.立方根与平方根的异同
课后作业
1.布置作业:从教材“习题6.2”中
1、2、 3、5.
2.完成同步测评练习册中本课时的习题.
