人教版九年级数学(下)28.2.2应用举例(2)(共16张PPT)
文档属性
| 名称 | 人教版九年级数学(下)28.2.2应用举例(2)(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 957.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 16:09:51 | ||
图片预览


文档简介
h
l
α
i
28.2.2应用举例(2)
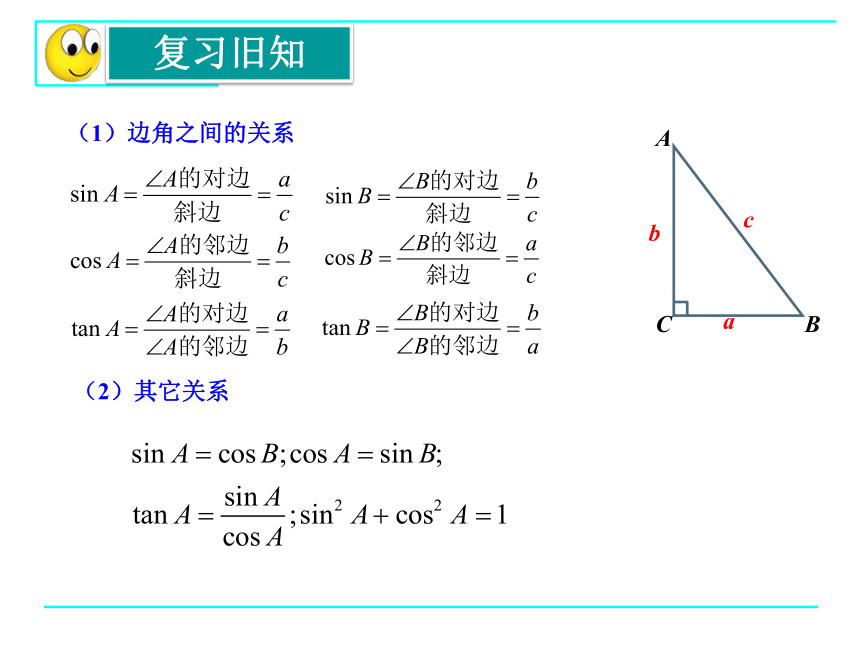
(1)边角之间的关系
A
B
a
b
c
C
复习旧知
(2)其它关系
60°
30°
P
B
C
A
引例
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80n
mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果保留根号)?
解:如图
∠APB=180°-60°-30°=90°
∠A=60°
在Rt△APB中
例题讲解
当海轮到达位于灯塔P的南偏东30°方向时,它距离灯塔P大约
海里.
65°
34°
P
B
C
A
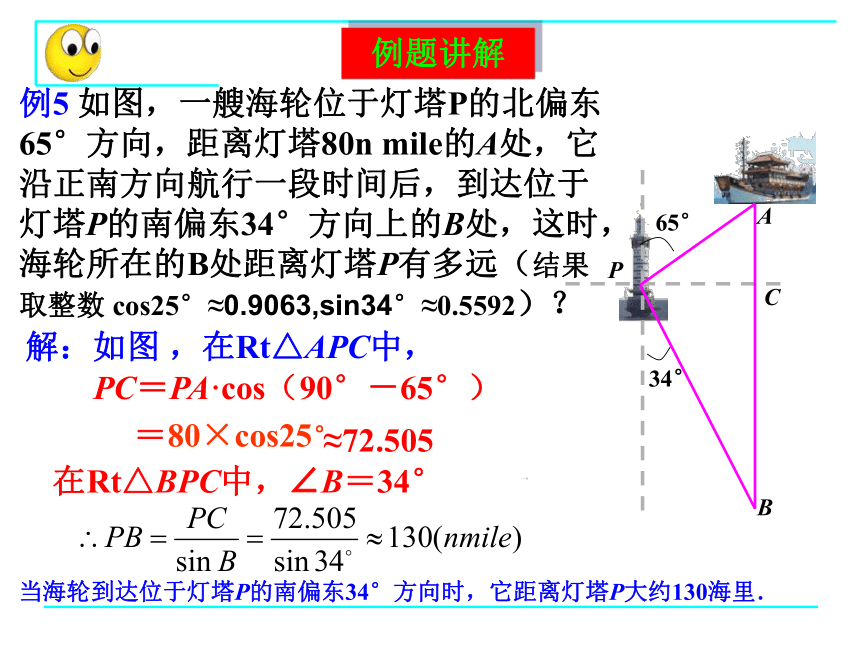
例5
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80n
mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数
cos25°≈0.9063,sin34°≈0.5592)?
解:如图
,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈72.505
在Rt△BPC中,∠B=34°
例题讲解
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130海里.
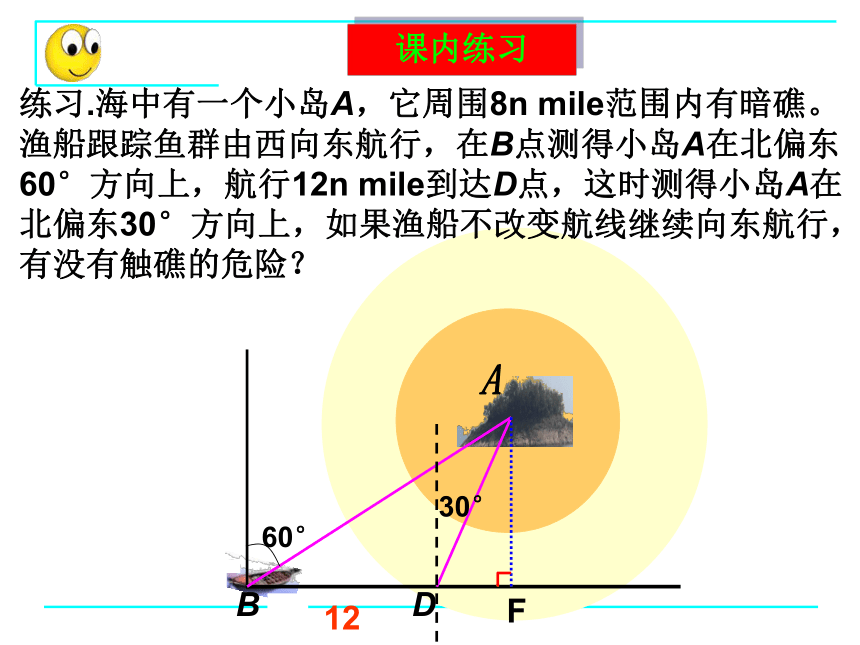
练习.海中有一个小岛A,它周围8n
mile范围内有暗礁。渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12n
mile到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
60°
12
30°
课内练习
B
A
D
F
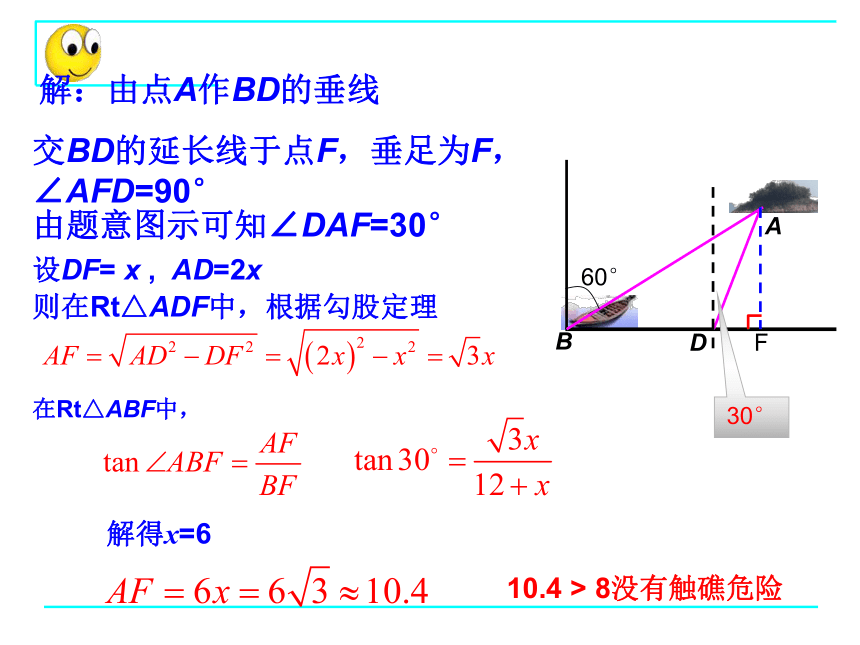
解:由点A作BD的垂线
交BD的延长线于点F,垂足为F,∠AFD=90°
由题意图示可知∠DAF=30°
设DF=
x
,
AD=2x
则在Rt△ADF中,根据勾股定理
在Rt△ABF中,
解得x=6
10.4
>
8没有触礁危险
30°
60°
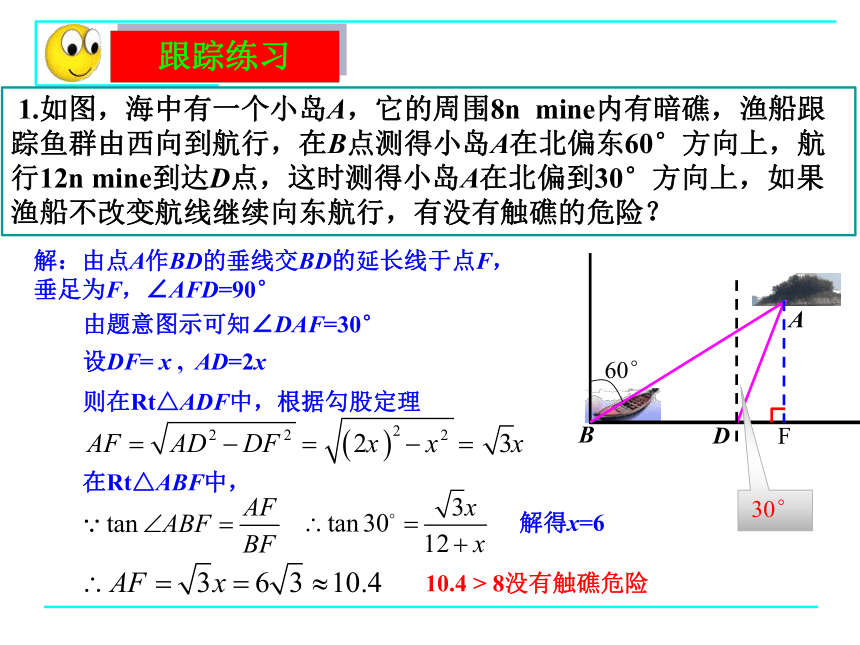
1.如图,海中有一个小岛A,它的周围8n
mine内有暗礁,渔船跟踪鱼群由西向到航行,在B点测得小岛A在北偏东60°方向上,航行12n
mine到达D点,这时测得小岛A在北偏到30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
解:由点A作BD的垂线交BD的延长线于点F,
垂足为F,∠AFD=90°
由题意图示可知∠DAF=30°
设DF=
x
,
AD=2x
则在Rt△ADF中,根据勾股定理
在Rt△ABF中,
解得x=6
10.4
>
8没有触礁危险
30°
60°
跟踪练宽度
显然,坡度越大,坡角α就越大,
坡面就越陡.
坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比)。
记作i
,
即
i
=
=tanα。
修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
坡面AB与水平面BC所形成的夹角∠ABC叫做坡角,记作α
一般地,线段BC的长度称为斜坡
AB的水平宽度,用l表示,线段AC
的长度称为斜坡AB的铅直高度,用h表示。
C
A
B
AB表示坡面
BC表示水平面
h
l
α
h
l
α
i
温馨提示
(1)坡度i不是坡角的度数,它是坡角的正切值,即i=tanα;
(2)坡度i也叫坡比,即i=
,
一般写成1:m的形式。
铅直高度
2、练习:
(1)一段坡面的坡角为60°,则坡度i=______;
跟踪练习
例题讲解
A
F
B
G
E
C
D
例5、某过街天桥的截面图形为梯形,如图所示,其中天桥斜面CD的坡度为:i=1:
,CD的长为10m,天桥另一斜面AB的坡角∠ABG=45°。
(1)写出过街天桥斜面AB的坡度;
(2)求DE的长;
(3)若决定对该天桥进行改建,使AB斜面的坡度变缓,将其45°坡角改为30°,方便过路群众,改建后斜面为AF,试计算此改建需占路面的宽度FB的长。(结果精确到0.01)
例题讲解
A
F
B
G
E
C
D
解:(1)设
AB的坡度为i′在Rt△AGB中,
∵
∠ABG=45°,∴AG=BG,
∴AB的坡度i′=tan
45°=1。
(2)在Rt△DEC中,∵
i=1:
,∴
tan
C
=
,
∴
∠C=30°。又∵CD=10cm,∴DE=5m
(3)由(1)(2),知AG=BG=DE=5m
在Rt△AFG中,∠F=
30°,
tanF=
,即
解得FB=
-5≈3.66(m)。
所以改建需占路面宽度FB长约3.66m。
B
A
D
F
E
C
6m
α
β
i=1:3
i=1:1.5
解:(1)在Rt△AFB中,∠AFB=90°
(2)在Rt△ABF中,
课内练习
如图,拦水坝的横断面为梯形ABCD,斜面坡度i=1:1.5是指坡面的铅直高度AF与水平宽度BF的比,斜面坡度i=1:3是指DE与CE的比。根据图中数据求:
(1)坡角α和β;
(2)斜坡AB的长(结果保留整数)
在Rt△CDE中,∠CED=90°
解:(1)在Rt△ABC中,
∠ACB=90°
课内练习
如图,在山坡上种树,要求两树间的水平距离是5.5m、测得斜坡的倾斜角是24度,求斜坡上相邻两树间的坡面距离(结果保留小数点后一位)
C
A
B
24°
故斜坡上相邻两树间的坡面距离约为6.0m。
综合提高
如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°。沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
,AB=10米,AE=15米。(i=1:
是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.
参考数据:
)
(1)BH=5m。
(2)CD≈2.7m。
45°
60°
B
C
D
H
A
E
1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
l
α
i
28.2.2应用举例(2)
(1)边角之间的关系
A
B
a
b
c
C
复习旧知
(2)其它关系
60°
30°
P
B
C
A
引例
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80n
mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果保留根号)?
解:如图
∠APB=180°-60°-30°=90°
∠A=60°
在Rt△APB中
例题讲解
当海轮到达位于灯塔P的南偏东30°方向时,它距离灯塔P大约
海里.
65°
34°
P
B
C
A
例5
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80n
mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数
cos25°≈0.9063,sin34°≈0.5592)?
解:如图
,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈72.505
在Rt△BPC中,∠B=34°
例题讲解
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130海里.
练习.海中有一个小岛A,它周围8n
mile范围内有暗礁。渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12n
mile到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
60°
12
30°
课内练习
B
A
D
F
解:由点A作BD的垂线
交BD的延长线于点F,垂足为F,∠AFD=90°
由题意图示可知∠DAF=30°
设DF=
x
,
AD=2x
则在Rt△ADF中,根据勾股定理
在Rt△ABF中,
解得x=6
10.4
>
8没有触礁危险
30°
60°
1.如图,海中有一个小岛A,它的周围8n
mine内有暗礁,渔船跟踪鱼群由西向到航行,在B点测得小岛A在北偏东60°方向上,航行12n
mine到达D点,这时测得小岛A在北偏到30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
解:由点A作BD的垂线交BD的延长线于点F,
垂足为F,∠AFD=90°
由题意图示可知∠DAF=30°
设DF=
x
,
AD=2x
则在Rt△ADF中,根据勾股定理
在Rt△ABF中,
解得x=6
10.4
>
8没有触礁危险
30°
60°
跟踪练宽度
显然,坡度越大,坡角α就越大,
坡面就越陡.
坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比)。
记作i
,
即
i
=
=tanα。
修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
坡面AB与水平面BC所形成的夹角∠ABC叫做坡角,记作α
一般地,线段BC的长度称为斜坡
AB的水平宽度,用l表示,线段AC
的长度称为斜坡AB的铅直高度,用h表示。
C
A
B
AB表示坡面
BC表示水平面
h
l
α
h
l
α
i
温馨提示
(1)坡度i不是坡角的度数,它是坡角的正切值,即i=tanα;
(2)坡度i也叫坡比,即i=
,
一般写成1:m的形式。
铅直高度
2、练习:
(1)一段坡面的坡角为60°,则坡度i=______;
跟踪练习
例题讲解
A
F
B
G
E
C
D
例5、某过街天桥的截面图形为梯形,如图所示,其中天桥斜面CD的坡度为:i=1:
,CD的长为10m,天桥另一斜面AB的坡角∠ABG=45°。
(1)写出过街天桥斜面AB的坡度;
(2)求DE的长;
(3)若决定对该天桥进行改建,使AB斜面的坡度变缓,将其45°坡角改为30°,方便过路群众,改建后斜面为AF,试计算此改建需占路面的宽度FB的长。(结果精确到0.01)
例题讲解
A
F
B
G
E
C
D
解:(1)设
AB的坡度为i′在Rt△AGB中,
∵
∠ABG=45°,∴AG=BG,
∴AB的坡度i′=tan
45°=1。
(2)在Rt△DEC中,∵
i=1:
,∴
tan
C
=
,
∴
∠C=30°。又∵CD=10cm,∴DE=5m
(3)由(1)(2),知AG=BG=DE=5m
在Rt△AFG中,∠F=
30°,
tanF=
,即
解得FB=
-5≈3.66(m)。
所以改建需占路面宽度FB长约3.66m。
B
A
D
F
E
C
6m
α
β
i=1:3
i=1:1.5
解:(1)在Rt△AFB中,∠AFB=90°
(2)在Rt△ABF中,
课内练习
如图,拦水坝的横断面为梯形ABCD,斜面坡度i=1:1.5是指坡面的铅直高度AF与水平宽度BF的比,斜面坡度i=1:3是指DE与CE的比。根据图中数据求:
(1)坡角α和β;
(2)斜坡AB的长(结果保留整数)
在Rt△CDE中,∠CED=90°
解:(1)在Rt△ABC中,
∠ACB=90°
课内练习
如图,在山坡上种树,要求两树间的水平距离是5.5m、测得斜坡的倾斜角是24度,求斜坡上相邻两树间的坡面距离(结果保留小数点后一位)
C
A
B
24°
故斜坡上相邻两树间的坡面距离约为6.0m。
综合提高
如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°。沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
,AB=10米,AE=15米。(i=1:
是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.
参考数据:
)
(1)BH=5m。
(2)CD≈2.7m。
45°
60°
B
C
D
H
A
E
1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
