人教版九年级下册数学课件——第27章 相似 复习课(共36张PPT)
文档属性
| 名称 | 人教版九年级下册数学课件——第27章 相似 复习课(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 12:39:49 | ||
图片预览





文档简介
第二十七章
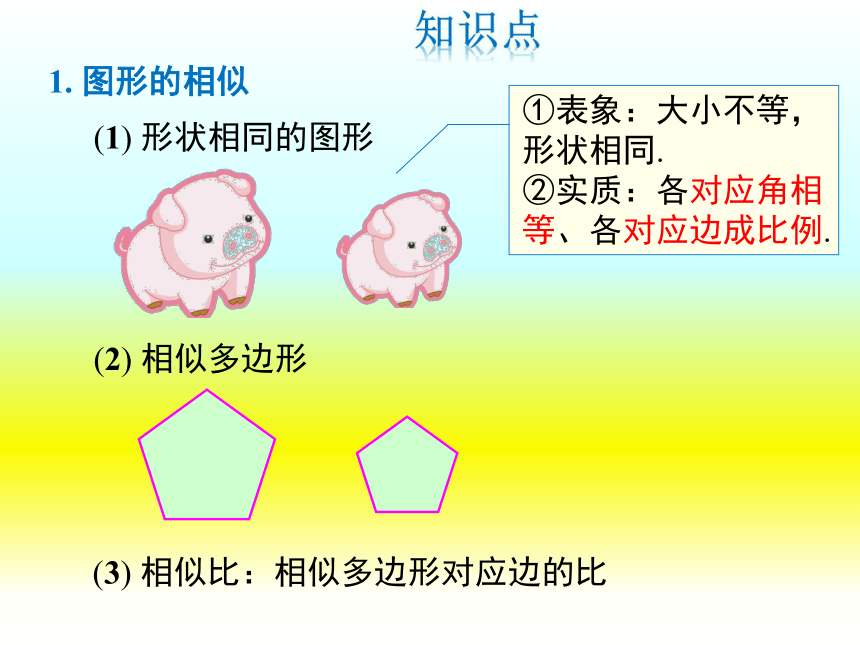
(1) 形状相同的图形
(2) 相似多边形
(3) 相似比:相似多边形对应边的比
1. 图形的相似
①表象:大小不等,形状相同.
②实质:各对应角相等、各对应边成比例.
?通过定义
?平行于三角形一边的直线
?三边成比例
?两边成比例且夹角相等
?两角分别相等
?两直角三角形的斜边和一条直角边成比例
(三个角分别相等,三条边成比例)
2. 相似三角形的判定
?对应角相等、对应边成比例
?对应高、中线、角平分线的比等于相似比
?周长比等于相似比
?面积比等于相似比的平方
3. 相似三角形的性质
(1) 测高
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺量的)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
(2) 测距
4. 相似三角形的应用
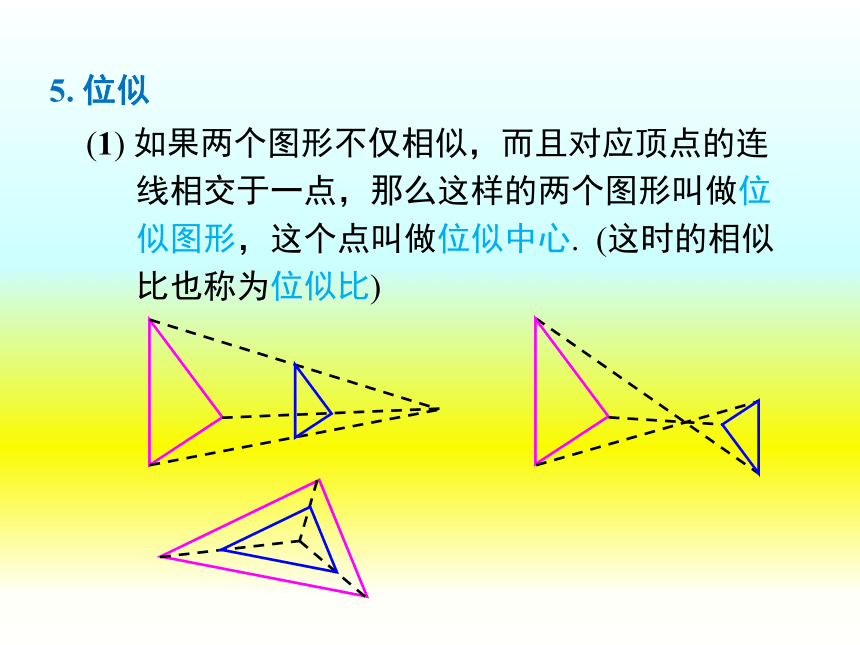
(1) 如果两个图形不仅相似,而且对应顶点的连
线相交于一点,那么这样的两个图形叫做位
似图形,这个点叫做位似中心. (这时的相似
比也称为位似比)
5. 位似
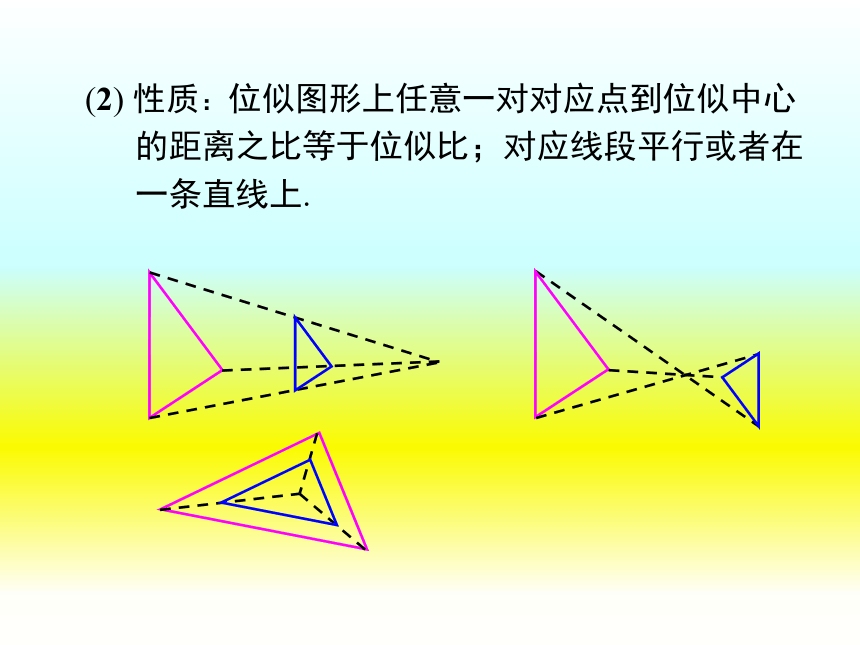
(2) 性质:位似图形上任意一对对应点到位似中心
的距离之比等于位似比;对应线段平行或者在
一条直线上.
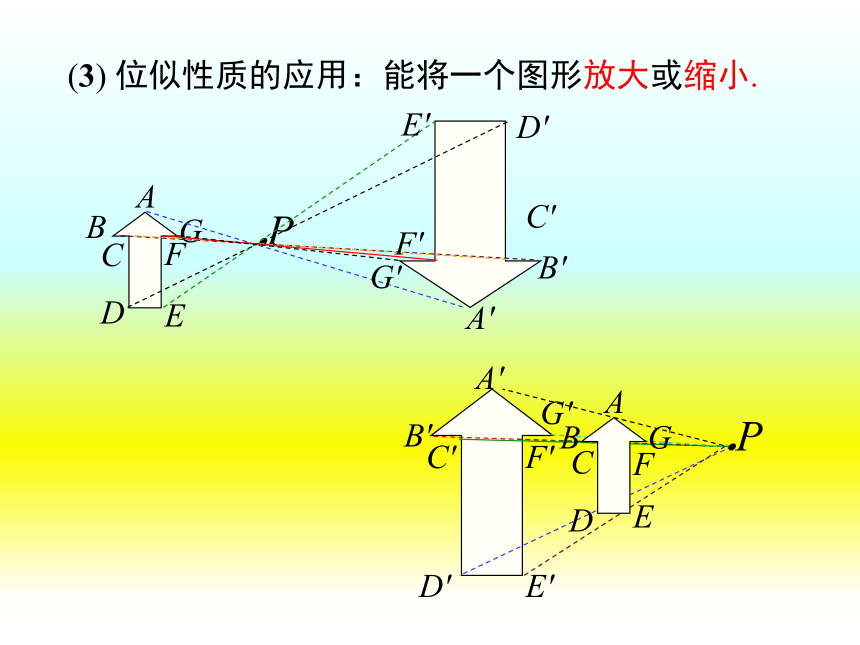
(3) 位似性质的应用:能将一个图形放大或缩小.
A
B
G
C
E
D
F
●P
B′
A′
C′
D′
E′
F′
G′
A′
B′
C′
D′
E′
F′
G′
A
B
G
C
E
D
F
●P
(4) 平面直角坐标系中的位似
当位似图形在原点同侧时,其对应顶点的坐标的比为 k;当位似图形在原点两侧时,对应顶点的坐标的比为-k.
相似三角形的判定和性质
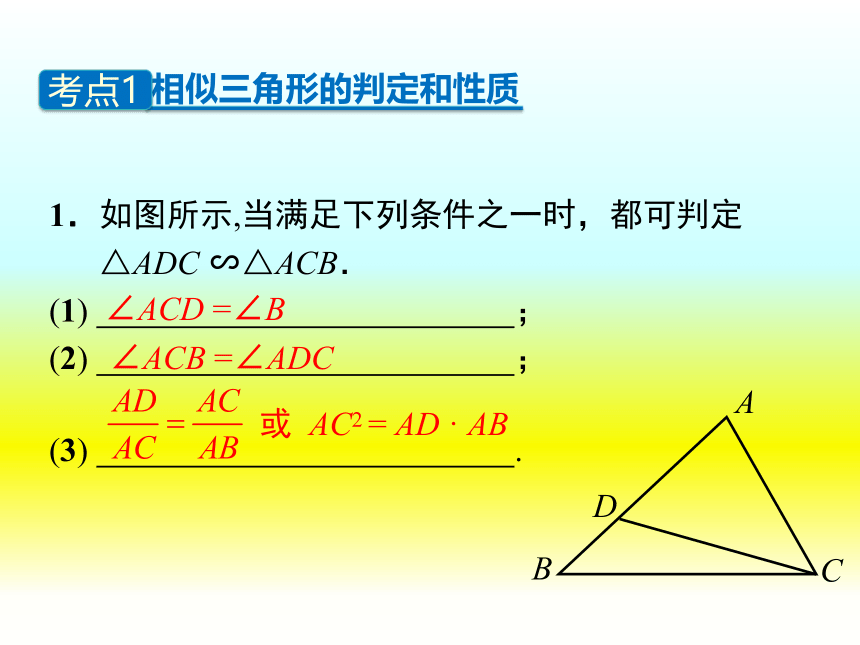
1.如图所示,当满足下列条件之一时,都可判定
△ADC ∽△ACB.
(1) ;
(2) ;
(3) .
∠ACD =∠B
∠ACB =∠ADC
B
C
A
D
或 AC2 = AD · AB
考点1
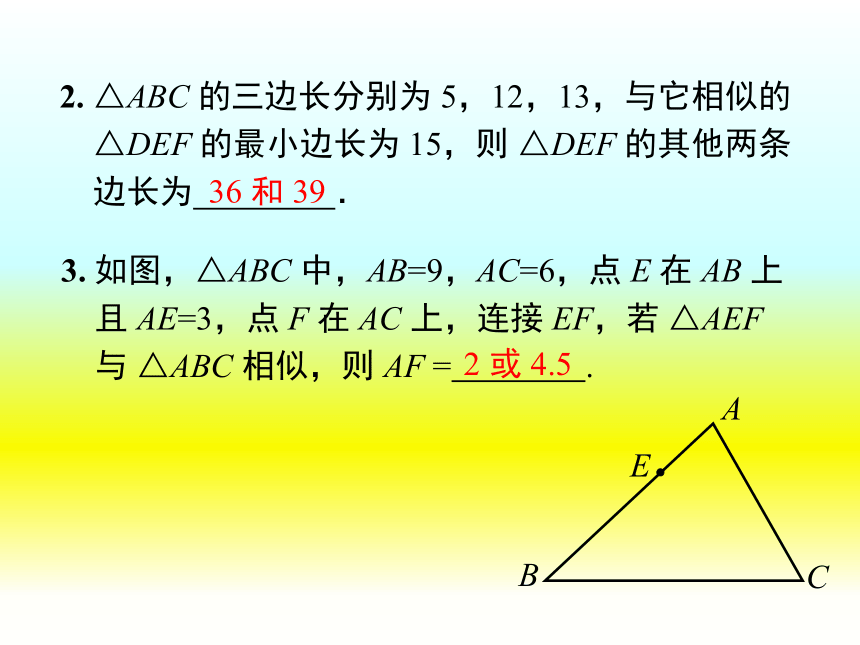
2. △ABC 的三边长分别为 5,12,13,与它相似的
△DEF 的最小边长为 15,则 △DEF 的其他两条
边长为 .
36 和 39
3. 如图,△ABC 中,AB=9,AC=6,点 E 在 AB 上
且 AE=3,点 F 在 AC 上,连接 EF,若 △AEF
与 △ABC 相似,则 AF = .
B
C
A
E
2 或 4.5
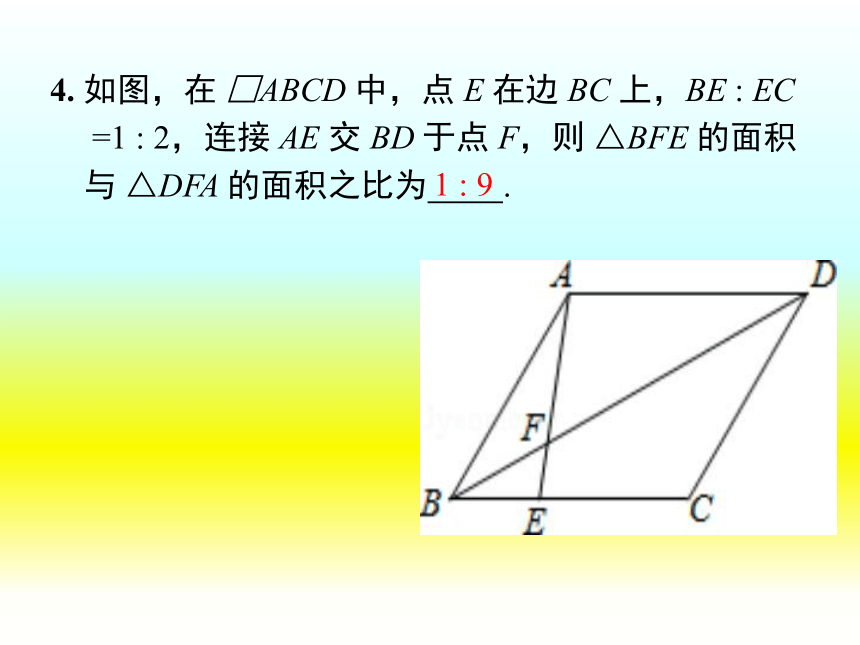
4. 如图,在 □ABCD 中,点 E 在边 BC 上,BE : EC
=1 : 2,连接 AE 交 BD 于点 F,则 △BFE 的面积
与 △DFA 的面积之比为 .
1 : 9
5. 如图,CD 是 ⊙O 的弦,AB 是直径,CD⊥AB,垂
足为 P,求证:PC2 = PA · PB.
B
·
A
C
D
O
P
证明:连接AC,BC.
∵AB是直径,
∴∠ACB=90°,
∴ ∠A + ∠B = 90°.
又 ∵CD⊥AB,∴∠CPB=90°,
∠PCB+∠B=90°.
又 ∠A=∠CPB,
∴ △APC ∽△CPB.
∴ PC2 = AP · PB.
∴
如图,△ABC 是一块锐角三角形材料,边 BC=120 mm,高 AD=80 mm,要把它加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在 AB、AC 上,这个正方形零件的边长是多少?
A
B
C
D
E
F
G
H
解:设正方形 EFHG 为加工成的
正方形零件,边 GH 在 BC
上,顶点 E、F 分别在AB、
AC上,△ABC 的高 AD 与边
EF 相交于点 M,设正方形的
边长为 x mm.
M
例1
∵ EF//BC,
∴△AEF∽△ABC,
又∵ AM=AD-MD=80-x,
解得 x = 48.
即这个正方形零件的边长是 48 mm.
A
B
C
D
E
F
G
H
M
则
∴
证明:∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∠ACF=120°.
∵CE是外角平分线,
∴∠ACE=60°,
∴∠BAC=∠ACE.
又∵∠ADB=∠CDE,
∴△ABD∽△CED.
如图,△ABC 是等边三角形,CE 是外角平分
线,点 D 在 AC 上,连接 BD 并延长与 CE 交于点 E.
(1) 求证:△ABD ∽△CED;
A
B
C
D
F
E
例2
(2) 若 AB = 6,AD = 2CD,求 BE 的长.
解:作 BM⊥AC 于点 M.
∵ AC=AB=6,
∴ AM=CM=3.
∵ AD = 2CD,
∴CD=2,AD=4,
MD=1.
A
B
C
D
F
E
M
在 Rt△BDM 中,
由(1) △ABD ∽△CED得,
即
∴
A
B
C
D
F
E
M
证明:连接AD,
∵∠DAC=∠DEC,∠EBC=∠DEC,
∴∠DAC=∠EBC.
∵AC 是 ⊙O 的直径,
∴∠ADC=90°,∴∠DCA+∠DAC=90°,
∴∠EBC+∠DCA=90°,∴∠BGC =180°-
(∠EBC+∠DCA)=90°,∴AC⊥BH.
已知:在 △ABC 中,以 AC 边为直径的 ⊙O 交BC 于点 D,在劣弧上取一点 E 使 ∠EBC =∠DEC,延长 BE 依次交 AC 于点 G,交 ⊙O 于 H.
(1) 求证:AC⊥BH;
A
B
C
D
G
E
O
H
例3
(2) 若 ∠ABC=45°,⊙O 的直径等于 10,BD = 8,
求 CE 的长.
A
B
C
D
G
E
O
H
解:∵∠BDA=180°-∠ADC=90°,
∠ABC=45°,∴∠BAD=45°,
∴ BD = AD.
∵ BD = 8,∴ AD = 8.
在 Rt△ADC中,AD = 8,AC = 10,
由勾股定理得 DC = 6,则 BC = BD + DC = 14.
∵∠EBC = ∠DEC,∠BCE = ∠ECD,
∴△BCE∽△ECD,∴BC : CE = CE : CD,
即 CE2 = BC · CD =14×6 = 84,∴ CE = 2.
相似的应用
如图,某一时刻一根 2 m 长的竹竿 EF 的影长 GE 为 1.2 m,此时,小红测得一棵被风吹斜的柏树与地面成 30°角,树顶端 B 在地面上的影子点 D
与 B 到垂直地面的落点 C 的距离是 3.6 m,求树 AB的长.
2m
1.2m
3.6m
考点2
例1
2m
1.2m
3.6m
解:如图,CD=3.6m,
∵△BDC∽△FGE,
∴ BC=6m.
在 Rt△ABC 中,
∵ ∠A=30°,
∴ AB=2BC=12 m,
即树长 AB 是 12 m.
即
∴
星期天,小丽和同学们在碧沙岗公园游玩,他们来到 1928 年冯玉祥将军为纪念北伐军阵亡将士所立的纪念碑前,小丽问:“这个纪念碑有多高呢?”请你利用初中数学知识,设计一种方案测量纪念碑的高度 (画出示意图),并说明理由.
例2
解:如图,线段 AB 为纪念碑,在地面上平放一面镜
子 E,人退后到 D 处,在镜子里恰好看见纪念碑
顶 A. 若人眼距地面距离为 CD,测量出 CD、DE、
BE的长,就可算出纪念碑 AB 的高.
根据 ,即可算出 AB 的高.
你还有其他方法吗?
理由:测量出CD、DE、BE的长,因为∠CED=∠AEB,∠D=∠B=90°,易得△ABE∽△CDE.
如图,小明同学跳起来把一个排球打在离地 2 m远的地上,然后反弹碰到墙上,如果她跳起击球时的高度是 1.8 m,排球落地点离墙的距离是 6 m,假设球一直沿直线运动,球能碰到墙面离地多高的地方?
A
B
O
C
D
2m
6m
1.8m
解:∵∠ABO=∠CDO=90°,
∠AOB=∠COD,
∴△AOB∽△COD.
∴
∴
解得 CD = 5.4m.
故球能碰到墙面离地 5.4m 高的地方.
A
B
O
C
D
2m
6m
1.8m
位似的性质及应用
1. 在如图所示的四个图形中,位似图形的个数为 ( )
A. 1个 B. 2个 C. 3个 D. 4个
C
考点3
2. 已知 △ABC ∽ △A′B′C′,下列图形中, △ABC 和
△A′B′C′ 不存在位似关系的是 ( )
B'
A(A')
C'
B
C
B'
A(A')
C'
B
C
B'
A(A')
C'
B
C
B'
A
C'
B
C
A'
A
B
C
D
B
3. 如图,DE∥AB,CE = 3BE,则 △ABC 与 △DEC
是以点 为位似中心的位似图形,其位似比为
,面积比为 .
D
A
E
B
C
C
4 : 3
16 : 9
4. 在平面直角坐标系中,点 A,B 的坐标分别为(-6,
3),(-12,9),△ABO 和 △A′B′O 是以原点 O 为
位似中心的位似图形. 若点 A′ 的坐标为 (2,-1) 则
点 B′ 的坐标为 .
(4,-3)
5. 找出下列图形的位似中心.
6. 如图,下面的网格中,每个小正方形的边长均为 1,
点 O 和 △ABC 的顶点均为小正方形的顶点.
A
B
C
(1) 在图中 △ABC 内部作 △A′B′C′,使 △A′B′C′ 和
△ABC 位似,且位似中心为点 O,位似比为 2 : 3.
O
A′
B′
C′
解:如图所示.
(2) 线段 AA′ 的长度是 .
7. 如图,△ABC 在方格纸中.
(1) 请在方格纸上建立平面直角坐标系,使A (2,3),
C (6,2),并求出 B 点坐标;
解:如图所示,
B (2,1).
x
y
O
(2) 以原点 O 为位似中心,位似比为 2,在第一象限内
将 △ABC 放大,画出放大后的图形 △A′B′C′;
x
y
O
A′
B′
C′
解:如图所示.
(3) 计算△A′B′C′的面积 S.
x
y
O
A′
B′
C′
解:
相似
相似图形
位似
相似多边形
相似三角形
性质
平面直角坐标系中的位似
应用
性质
判定
平行线分线段成比例
定义
定义、判定、性质
(1) 形状相同的图形
(2) 相似多边形
(3) 相似比:相似多边形对应边的比
1. 图形的相似
①表象:大小不等,形状相同.
②实质:各对应角相等、各对应边成比例.
?通过定义
?平行于三角形一边的直线
?三边成比例
?两边成比例且夹角相等
?两角分别相等
?两直角三角形的斜边和一条直角边成比例
(三个角分别相等,三条边成比例)
2. 相似三角形的判定
?对应角相等、对应边成比例
?对应高、中线、角平分线的比等于相似比
?周长比等于相似比
?面积比等于相似比的平方
3. 相似三角形的性质
(1) 测高
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺量的)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
(2) 测距
4. 相似三角形的应用
(1) 如果两个图形不仅相似,而且对应顶点的连
线相交于一点,那么这样的两个图形叫做位
似图形,这个点叫做位似中心. (这时的相似
比也称为位似比)
5. 位似
(2) 性质:位似图形上任意一对对应点到位似中心
的距离之比等于位似比;对应线段平行或者在
一条直线上.
(3) 位似性质的应用:能将一个图形放大或缩小.
A
B
G
C
E
D
F
●P
B′
A′
C′
D′
E′
F′
G′
A′
B′
C′
D′
E′
F′
G′
A
B
G
C
E
D
F
●P
(4) 平面直角坐标系中的位似
当位似图形在原点同侧时,其对应顶点的坐标的比为 k;当位似图形在原点两侧时,对应顶点的坐标的比为-k.
相似三角形的判定和性质
1.如图所示,当满足下列条件之一时,都可判定
△ADC ∽△ACB.
(1) ;
(2) ;
(3) .
∠ACD =∠B
∠ACB =∠ADC
B
C
A
D
或 AC2 = AD · AB
考点1
2. △ABC 的三边长分别为 5,12,13,与它相似的
△DEF 的最小边长为 15,则 △DEF 的其他两条
边长为 .
36 和 39
3. 如图,△ABC 中,AB=9,AC=6,点 E 在 AB 上
且 AE=3,点 F 在 AC 上,连接 EF,若 △AEF
与 △ABC 相似,则 AF = .
B
C
A
E
2 或 4.5
4. 如图,在 □ABCD 中,点 E 在边 BC 上,BE : EC
=1 : 2,连接 AE 交 BD 于点 F,则 △BFE 的面积
与 △DFA 的面积之比为 .
1 : 9
5. 如图,CD 是 ⊙O 的弦,AB 是直径,CD⊥AB,垂
足为 P,求证:PC2 = PA · PB.
B
·
A
C
D
O
P
证明:连接AC,BC.
∵AB是直径,
∴∠ACB=90°,
∴ ∠A + ∠B = 90°.
又 ∵CD⊥AB,∴∠CPB=90°,
∠PCB+∠B=90°.
又 ∠A=∠CPB,
∴ △APC ∽△CPB.
∴ PC2 = AP · PB.
∴
如图,△ABC 是一块锐角三角形材料,边 BC=120 mm,高 AD=80 mm,要把它加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在 AB、AC 上,这个正方形零件的边长是多少?
A
B
C
D
E
F
G
H
解:设正方形 EFHG 为加工成的
正方形零件,边 GH 在 BC
上,顶点 E、F 分别在AB、
AC上,△ABC 的高 AD 与边
EF 相交于点 M,设正方形的
边长为 x mm.
M
例1
∵ EF//BC,
∴△AEF∽△ABC,
又∵ AM=AD-MD=80-x,
解得 x = 48.
即这个正方形零件的边长是 48 mm.
A
B
C
D
E
F
G
H
M
则
∴
证明:∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∠ACF=120°.
∵CE是外角平分线,
∴∠ACE=60°,
∴∠BAC=∠ACE.
又∵∠ADB=∠CDE,
∴△ABD∽△CED.
如图,△ABC 是等边三角形,CE 是外角平分
线,点 D 在 AC 上,连接 BD 并延长与 CE 交于点 E.
(1) 求证:△ABD ∽△CED;
A
B
C
D
F
E
例2
(2) 若 AB = 6,AD = 2CD,求 BE 的长.
解:作 BM⊥AC 于点 M.
∵ AC=AB=6,
∴ AM=CM=3.
∵ AD = 2CD,
∴CD=2,AD=4,
MD=1.
A
B
C
D
F
E
M
在 Rt△BDM 中,
由(1) △ABD ∽△CED得,
即
∴
A
B
C
D
F
E
M
证明:连接AD,
∵∠DAC=∠DEC,∠EBC=∠DEC,
∴∠DAC=∠EBC.
∵AC 是 ⊙O 的直径,
∴∠ADC=90°,∴∠DCA+∠DAC=90°,
∴∠EBC+∠DCA=90°,∴∠BGC =180°-
(∠EBC+∠DCA)=90°,∴AC⊥BH.
已知:在 △ABC 中,以 AC 边为直径的 ⊙O 交BC 于点 D,在劣弧上取一点 E 使 ∠EBC =∠DEC,延长 BE 依次交 AC 于点 G,交 ⊙O 于 H.
(1) 求证:AC⊥BH;
A
B
C
D
G
E
O
H
例3
(2) 若 ∠ABC=45°,⊙O 的直径等于 10,BD = 8,
求 CE 的长.
A
B
C
D
G
E
O
H
解:∵∠BDA=180°-∠ADC=90°,
∠ABC=45°,∴∠BAD=45°,
∴ BD = AD.
∵ BD = 8,∴ AD = 8.
在 Rt△ADC中,AD = 8,AC = 10,
由勾股定理得 DC = 6,则 BC = BD + DC = 14.
∵∠EBC = ∠DEC,∠BCE = ∠ECD,
∴△BCE∽△ECD,∴BC : CE = CE : CD,
即 CE2 = BC · CD =14×6 = 84,∴ CE = 2.
相似的应用
如图,某一时刻一根 2 m 长的竹竿 EF 的影长 GE 为 1.2 m,此时,小红测得一棵被风吹斜的柏树与地面成 30°角,树顶端 B 在地面上的影子点 D
与 B 到垂直地面的落点 C 的距离是 3.6 m,求树 AB的长.
2m
1.2m
3.6m
考点2
例1
2m
1.2m
3.6m
解:如图,CD=3.6m,
∵△BDC∽△FGE,
∴ BC=6m.
在 Rt△ABC 中,
∵ ∠A=30°,
∴ AB=2BC=12 m,
即树长 AB 是 12 m.
即
∴
星期天,小丽和同学们在碧沙岗公园游玩,他们来到 1928 年冯玉祥将军为纪念北伐军阵亡将士所立的纪念碑前,小丽问:“这个纪念碑有多高呢?”请你利用初中数学知识,设计一种方案测量纪念碑的高度 (画出示意图),并说明理由.
例2
解:如图,线段 AB 为纪念碑,在地面上平放一面镜
子 E,人退后到 D 处,在镜子里恰好看见纪念碑
顶 A. 若人眼距地面距离为 CD,测量出 CD、DE、
BE的长,就可算出纪念碑 AB 的高.
根据 ,即可算出 AB 的高.
你还有其他方法吗?
理由:测量出CD、DE、BE的长,因为∠CED=∠AEB,∠D=∠B=90°,易得△ABE∽△CDE.
如图,小明同学跳起来把一个排球打在离地 2 m远的地上,然后反弹碰到墙上,如果她跳起击球时的高度是 1.8 m,排球落地点离墙的距离是 6 m,假设球一直沿直线运动,球能碰到墙面离地多高的地方?
A
B
O
C
D
2m
6m
1.8m
解:∵∠ABO=∠CDO=90°,
∠AOB=∠COD,
∴△AOB∽△COD.
∴
∴
解得 CD = 5.4m.
故球能碰到墙面离地 5.4m 高的地方.
A
B
O
C
D
2m
6m
1.8m
位似的性质及应用
1. 在如图所示的四个图形中,位似图形的个数为 ( )
A. 1个 B. 2个 C. 3个 D. 4个
C
考点3
2. 已知 △ABC ∽ △A′B′C′,下列图形中, △ABC 和
△A′B′C′ 不存在位似关系的是 ( )
B'
A(A')
C'
B
C
B'
A(A')
C'
B
C
B'
A(A')
C'
B
C
B'
A
C'
B
C
A'
A
B
C
D
B
3. 如图,DE∥AB,CE = 3BE,则 △ABC 与 △DEC
是以点 为位似中心的位似图形,其位似比为
,面积比为 .
D
A
E
B
C
C
4 : 3
16 : 9
4. 在平面直角坐标系中,点 A,B 的坐标分别为(-6,
3),(-12,9),△ABO 和 △A′B′O 是以原点 O 为
位似中心的位似图形. 若点 A′ 的坐标为 (2,-1) 则
点 B′ 的坐标为 .
(4,-3)
5. 找出下列图形的位似中心.
6. 如图,下面的网格中,每个小正方形的边长均为 1,
点 O 和 △ABC 的顶点均为小正方形的顶点.
A
B
C
(1) 在图中 △ABC 内部作 △A′B′C′,使 △A′B′C′ 和
△ABC 位似,且位似中心为点 O,位似比为 2 : 3.
O
A′
B′
C′
解:如图所示.
(2) 线段 AA′ 的长度是 .
7. 如图,△ABC 在方格纸中.
(1) 请在方格纸上建立平面直角坐标系,使A (2,3),
C (6,2),并求出 B 点坐标;
解:如图所示,
B (2,1).
x
y
O
(2) 以原点 O 为位似中心,位似比为 2,在第一象限内
将 △ABC 放大,画出放大后的图形 △A′B′C′;
x
y
O
A′
B′
C′
解:如图所示.
(3) 计算△A′B′C′的面积 S.
x
y
O
A′
B′
C′
解:
相似
相似图形
位似
相似多边形
相似三角形
性质
平面直角坐标系中的位似
应用
性质
判定
平行线分线段成比例
定义
定义、判定、性质
