利用函数性质判定方程解的存在
图片预览







文档简介
(共20张PPT)
利用函数性质
判定
方程解的存在
X
Y
A
M
B
O
10m
(1,40/3)
(0,10)
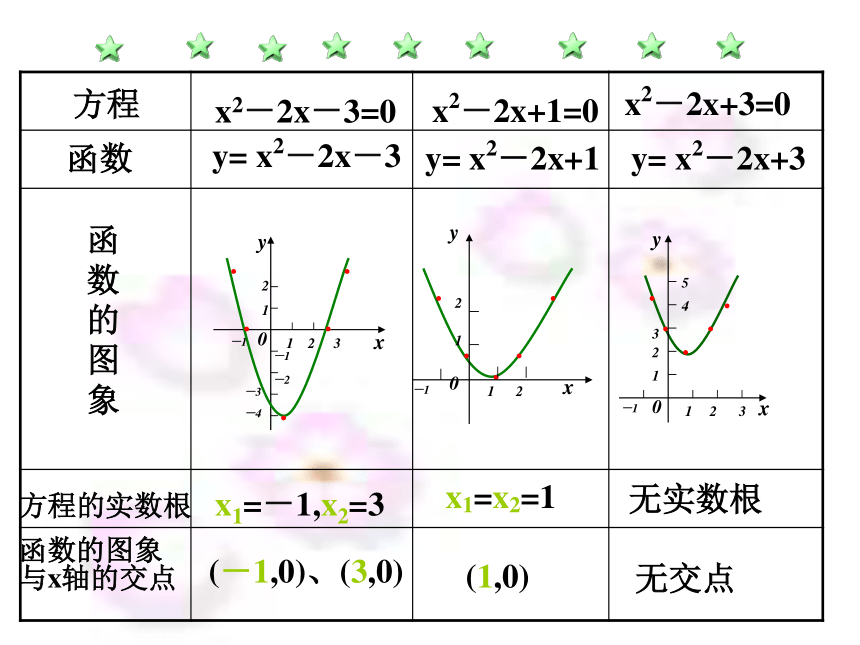
思考:一元二次方程
ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
y
x
0
-1
2
1
1
2
y= x2-2x+3
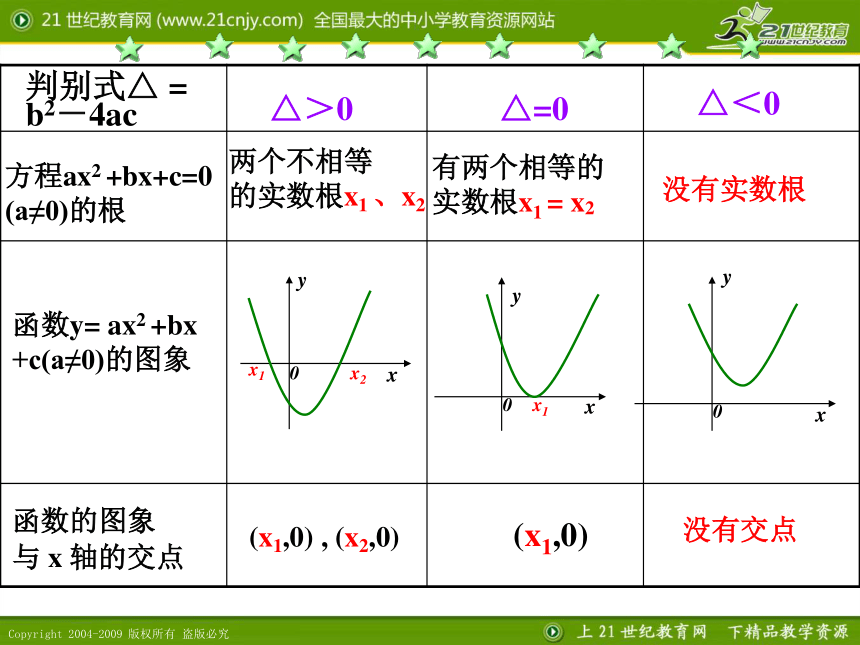
方程ax2 +bx+c=0
(a≠0)的根
函数y= ax2 +bx
+c(a≠0)的图象
判别式△ =
b2-4ac
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
没有实数根
x
y
x1
x2
0
x
y
0
x1
x
y
0
(x1,0) , (x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 、x2
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数
y=f(x)的零点。
函数零点的定义:
注意:
1.零点指的是一个实数;
零点是一个点吗
函数都有零点吗
2.不是所有函数都有零点.
如:
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
y
x
0
-1
2
1
1
2
y= x2-2x+3
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
等价关系
例题与练习:
练习:利用函数图象判断下列方程有没有根,有几个根:
(1)-x2+3x+5=0;
(2)2x(x-2)=-3;
(3) x2 =4x-4;
(4)5 x2 +2x=3 x2 +5.
例1 .判断方程 解的存在.
1(1)解:令f(x)=-x2+3x+5,
作出函数f(x)的图象,如下:
.
.
.
.
.
x
y
0
-1
3
2
1
4
8
6
2
-2
4
它与x轴有两个交点,所以方程-x2+3x+5=0有两个不相等的实数根。
1(1) -x2+3x+5=0
课堂练习
1(2)解:2x(x-2)=-3可化为
2x2-4x+3=0,令f(x)= 2x2-4x
+3 , 作出函数f(x)的图象,如下:
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
它与x轴没有交点,所以方程2x(x-2)=-3无实数根。
1(2) 2x(x-2)=-3
课堂练习
1(3)解:x2 =4x-4可化为x2-4x
+4=0,令f(x)= x2-4x+4,作出
函数f(x)的图象,如下:
.
.
.
.
.
它与x轴只有一个交点,所以方程x2 =4x-4有两个相等的实数根。
x
y
0
-1
3
2
1
1
2
5
4
3
6
4
1(3) x2 =4x-4
课堂练习
1(4)解:5x2 +2x=3x2 +5可化为
2x2 +2x-5=0,令f(x)=2x2+
2x-5 , 作出函数f(x)的图象,
如下:
x
y
0
-1
3
2
1
1
2
-1
-3
-3
-4
3
-6
-5
4
-4
-2
-2
.
.
.
.
.
它与x轴有两个交点,所以
方程5x2 +2x=3x2 +5有两个不
相等的实数根。
1(4) 5 x2 +2x=3 x2 +5
课堂练习
y=-x2-x+20; (2)y=2x-1;
拓展:求下列函数的零点。
评注:求函数的零点就是求相应的方程的根,一般可以借助求根公式或因式分解等办法,求出方程的根,从而得出函数的零点。
0
1
2
3
4
5
-1
-2
1
2
3
4
5
-1
-2
-3
-4
x
y
探究
结论
例
例2
例4
已知函数 问:方程
在区间[-1,0]上有没有实数解
例3 P116\例3
练习:
课堂小结:
课后作业:
1、求下列函数的零点:(1)y=-x2+6x+7;
(2)y=x3-4x。
2、若函数f(x)=x2-ax-b的两个零点是2和3,求loga25 + b2。
1、函数零点的定义;
2、函数的零点与方程的根的关系;
3、确定函数的零点的方法。
A
O
B
M
利用函数性质
判定
方程解的存在
X
Y
A
M
B
O
10m
(1,40/3)
(0,10)
思考:一元二次方程
ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
y
x
0
-1
2
1
1
2
y= x2-2x+3
方程ax2 +bx+c=0
(a≠0)的根
函数y= ax2 +bx
+c(a≠0)的图象
判别式△ =
b2-4ac
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
没有实数根
x
y
x1
x2
0
x
y
0
x1
x
y
0
(x1,0) , (x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 、x2
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数
y=f(x)的零点。
函数零点的定义:
注意:
1.零点指的是一个实数;
零点是一个点吗
函数都有零点吗
2.不是所有函数都有零点.
如:
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
.
.
.
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
y
x
0
-1
2
1
1
2
y= x2-2x+3
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
等价关系
例题与练习:
练习:利用函数图象判断下列方程有没有根,有几个根:
(1)-x2+3x+5=0;
(2)2x(x-2)=-3;
(3) x2 =4x-4;
(4)5 x2 +2x=3 x2 +5.
例1 .判断方程 解的存在.
1(1)解:令f(x)=-x2+3x+5,
作出函数f(x)的图象,如下:
.
.
.
.
.
x
y
0
-1
3
2
1
4
8
6
2
-2
4
它与x轴有两个交点,所以方程-x2+3x+5=0有两个不相等的实数根。
1(1) -x2+3x+5=0
课堂练习
1(2)解:2x(x-2)=-3可化为
2x2-4x+3=0,令f(x)= 2x2-4x
+3 , 作出函数f(x)的图象,如下:
x
y
0
-1
3
2
1
1
2
5
4
3
.
.
.
.
.
它与x轴没有交点,所以方程2x(x-2)=-3无实数根。
1(2) 2x(x-2)=-3
课堂练习
1(3)解:x2 =4x-4可化为x2-4x
+4=0,令f(x)= x2-4x+4,作出
函数f(x)的图象,如下:
.
.
.
.
.
它与x轴只有一个交点,所以方程x2 =4x-4有两个相等的实数根。
x
y
0
-1
3
2
1
1
2
5
4
3
6
4
1(3) x2 =4x-4
课堂练习
1(4)解:5x2 +2x=3x2 +5可化为
2x2 +2x-5=0,令f(x)=2x2+
2x-5 , 作出函数f(x)的图象,
如下:
x
y
0
-1
3
2
1
1
2
-1
-3
-3
-4
3
-6
-5
4
-4
-2
-2
.
.
.
.
.
它与x轴有两个交点,所以
方程5x2 +2x=3x2 +5有两个不
相等的实数根。
1(4) 5 x2 +2x=3 x2 +5
课堂练习
y=-x2-x+20; (2)y=2x-1;
拓展:求下列函数的零点。
评注:求函数的零点就是求相应的方程的根,一般可以借助求根公式或因式分解等办法,求出方程的根,从而得出函数的零点。
0
1
2
3
4
5
-1
-2
1
2
3
4
5
-1
-2
-3
-4
x
y
探究
结论
例
例2
例4
已知函数 问:方程
在区间[-1,0]上有没有实数解
例3 P116\例3
练习:
课堂小结:
课后作业:
1、求下列函数的零点:(1)y=-x2+6x+7;
(2)y=x3-4x。
2、若函数f(x)=x2-ax-b的两个零点是2和3,求loga25 + b2。
1、函数零点的定义;
2、函数的零点与方程的根的关系;
3、确定函数的零点的方法。
A
O
B
M
