人教版七年级数学下册 第九章不等式与不等式组 9.3 一元一次不等式组(第一课时)(共22张PPT)
文档属性
| 名称 | 人教版七年级数学下册 第九章不等式与不等式组 9.3 一元一次不等式组(第一课时)(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 17:37:20 | ||
图片预览







文档简介
泮水中学七年级数学课件
第九章 不等式与不等式组
9.3 一元一次不等式组
1.通过具体操作,在解一元一次不等式组的过程中形成正确的解不等式组的思路与方法;(重点、难点)
2.掌握在数轴上正确表示一元一次不等式组的解集的方法.
学习目标
问题:
用每分钟抽30t水的抽水机来抽污水管道积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用的时间的范围是什么?
解:设用xmin将污水抽完,则x满足
类似于方程组的概念,你能说出一元一次不等式组的概念吗?
能用你学过的知识分析一下吗?
30x>1200 (1)
30x<1500 (2)
新课引入
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量是两个或者多个。
类似于方程组,把两个或两个以上含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组。
概念归纳
判断下列不等式组是否为一元一次不等式组:
×
×
√
√
针对训练
思考:怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
归纳:我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
概念归纳
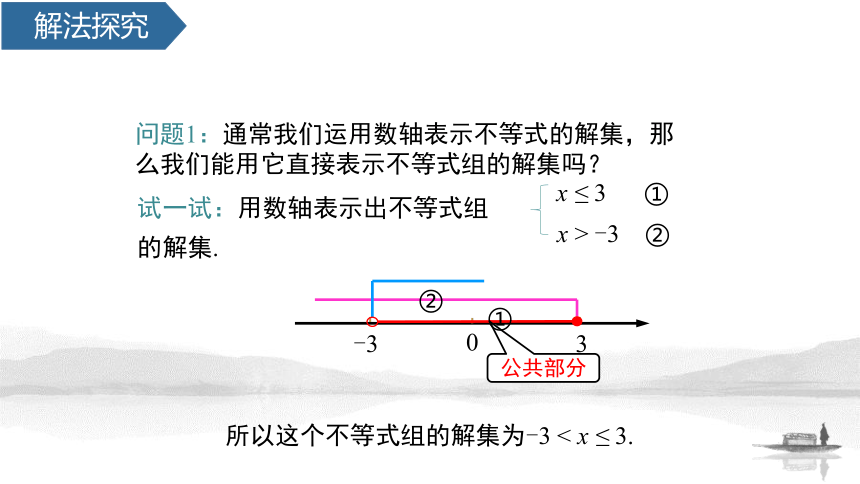
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试:用数轴表示出不等式组 的解集.
所以这个不等式组的解集为-3 < x ≤ 3.
x > -3 ②
x ≤ 3 ①
0
-3
3
公共部分
①
②
解法探究
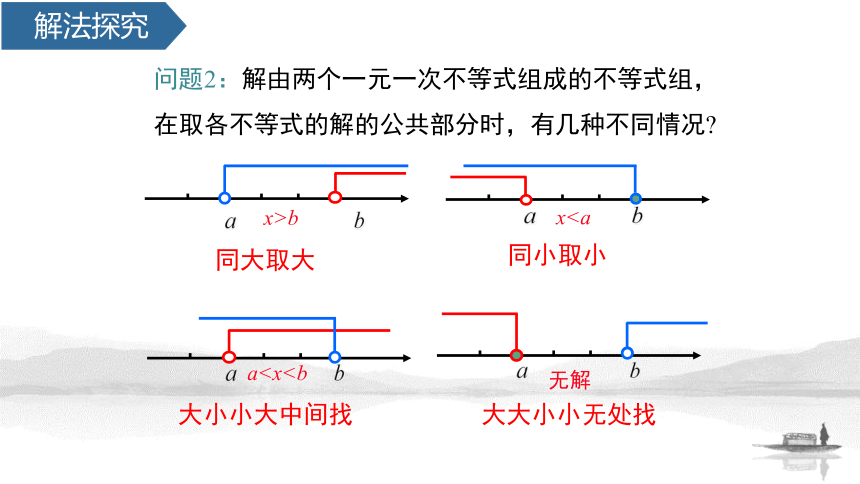
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
解法探究
解不等式②,得
x <-3.
例1 解不等式组:
解: 解不等式①,得
x ≤ 3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是 x<-3.
典例精讲
例2 解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,
如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
典例精讲
例3 解不等式组:
解 解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
由图可以看出这两个不等式的解集没有公共部分.所以,这个不等式组无解.
0
-2
3
典例精讲
例4 已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3+2b= -1
解得 a=1 , b= - 2
所以(a+1)(b-1)=2×(-3)=-6
典例精讲
解一元一次不等式组的解题步骤:
⑴求出不等式组中各个不等式的解集;
⑵利用数轴,找出这些不等式解集的 公共部分;
⑶根据几个不等式解集的公共部分,写
出 这个不等式组的解集。
解法归纳
1.(丽水·中考)不等式组 的解集在数轴上
表示为( )
【解析】选C. 解不等式①得x>1,解不等式
②得:x≥2,表示在数轴上为C选项.
A
B
C
D
随堂练习
2.(义乌·中考)不等式组 的解集在数轴
上表示为( )
1
0
2
A
1
0
2
B
1
0
2
C
1
0
2
D
【解析】选C.解3x+2>5,得x>1, 解5-2x≥1,得x≤2,所以不等式组的解集为1随堂练习
3.(苏州·中考)不等式组 的所有整数
解之和是( )
A.9 B.12 C.13 D.15
【解析】选B.解不等式组得3≤x<6,故其所有整数解为3,4,5,和为12.
随堂练习
0
8
4.解不等式组
②
①
【解析】解不等式①,得,
解不等式②,得,
把不等式①和②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解.
随堂练习
【解析】解不等式①,得
解不等式②,得
把不等式①和②的解集在数轴上表示出来:
0 1 2 3 4
所以不等式组的解集为
5.解不等式组
②
①
随堂练习
试求不等式组 的解集.
【解析】解不等式①,得 x>-2
解不等式②,得 x>3
解不等式③,得 x≤6
把不等式①,②,③的解集表示在同一数轴上,如下图:
-2 -1 0 1 2 3 4 5 6
○
●
○
所以,不等式组的解集是3 < x ≤ 6.
① ② ③
拓展提高
怎样求不等式 的解集?
【解析】原不等式可化为两个不等式组:
或
即 或
解(1)得 , 解(2)得 .
所以原不等式的解集是 或 .
随堂练习
1. 由几个含有相同未知数的一元一次不等式所组成的不等式组叫做一元一次不等式组 .
2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(1)
求出不等式组中各个不等式的解集
(2) 利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集。
(找不到公共部分则不等式组无解)
课堂小结
感谢您的聆听
第九章 不等式与不等式组
9.3 一元一次不等式组
1.通过具体操作,在解一元一次不等式组的过程中形成正确的解不等式组的思路与方法;(重点、难点)
2.掌握在数轴上正确表示一元一次不等式组的解集的方法.
学习目标
问题:
用每分钟抽30t水的抽水机来抽污水管道积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用的时间的范围是什么?
解:设用xmin将污水抽完,则x满足
类似于方程组的概念,你能说出一元一次不等式组的概念吗?
能用你学过的知识分析一下吗?
30x>1200 (1)
30x<1500 (2)
新课引入
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量是两个或者多个。
类似于方程组,把两个或两个以上含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组。
概念归纳
判断下列不等式组是否为一元一次不等式组:
×
×
√
√
针对训练
思考:怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
归纳:我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
概念归纳
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试:用数轴表示出不等式组 的解集.
所以这个不等式组的解集为-3 < x ≤ 3.
x > -3 ②
x ≤ 3 ①
0
-3
3
公共部分
①
②
解法探究
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa
解法探究
解不等式②,得
x <-3.
例1 解不等式组:
解: 解不等式①,得
x ≤ 3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是 x<-3.
典例精讲
例2 解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,
如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
典例精讲
例3 解不等式组:
解 解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
由图可以看出这两个不等式的解集没有公共部分.所以,这个不等式组无解.
0
-2
3
典例精讲
例4 已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3+2b= -1
解得 a=1 , b= - 2
所以(a+1)(b-1)=2×(-3)=-6
典例精讲
解一元一次不等式组的解题步骤:
⑴求出不等式组中各个不等式的解集;
⑵利用数轴,找出这些不等式解集的 公共部分;
⑶根据几个不等式解集的公共部分,写
出 这个不等式组的解集。
解法归纳
1.(丽水·中考)不等式组 的解集在数轴上
表示为( )
【解析】选C. 解不等式①得x>1,解不等式
②得:x≥2,表示在数轴上为C选项.
A
B
C
D
随堂练习
2.(义乌·中考)不等式组 的解集在数轴
上表示为( )
1
0
2
A
1
0
2
B
1
0
2
C
1
0
2
D
【解析】选C.解3x+2>5,得x>1, 解5-2x≥1,得x≤2,所以不等式组的解集为1
3.(苏州·中考)不等式组 的所有整数
解之和是( )
A.9 B.12 C.13 D.15
【解析】选B.解不等式组得3≤x<6,故其所有整数解为3,4,5,和为12.
随堂练习
0
8
4.解不等式组
②
①
【解析】解不等式①,得,
解不等式②,得,
把不等式①和②的解集在数轴上表示出来:
这两个不等式的解集没有公共部分,所以不等式组无解.
随堂练习
【解析】解不等式①,得
解不等式②,得
把不等式①和②的解集在数轴上表示出来:
0 1 2 3 4
所以不等式组的解集为
5.解不等式组
②
①
随堂练习
试求不等式组 的解集.
【解析】解不等式①,得 x>-2
解不等式②,得 x>3
解不等式③,得 x≤6
把不等式①,②,③的解集表示在同一数轴上,如下图:
-2 -1 0 1 2 3 4 5 6
○
●
○
所以,不等式组的解集是3 < x ≤ 6.
① ② ③
拓展提高
怎样求不等式 的解集?
【解析】原不等式可化为两个不等式组:
或
即 或
解(1)得 , 解(2)得 .
所以原不等式的解集是 或 .
随堂练习
1. 由几个含有相同未知数的一元一次不等式所组成的不等式组叫做一元一次不等式组 .
2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(1)
求出不等式组中各个不等式的解集
(2) 利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集。
(找不到公共部分则不等式组无解)
课堂小结
感谢您的聆听
