人教版七年级下册课件 10.1.2抽样调查(共28张PPT)
文档属性
| 名称 | 人教版七年级下册课件 10.1.2抽样调查(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 632.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 17:45:53 | ||
图片预览








文档简介
第十章 数据的收集、整理与描述
10.1 统计调查
2 抽样调查
一天,爸爸叫儿子小华去买一盒火柴.临出门前,爸爸嘱咐儿子要买能划燃的火柴.小华拿着钱出门了,过了好一会儿,小华才回到家.
“火柴能划燃吗?”爸爸问.
“都能划燃.”
“你这么肯定?”
小华递过一盒划过的火柴,兴奋地说:“我每根都试过啦.”
思考:得到火柴能否划燃的信息准确吗? 这样做好吗?
小华这样买火柴对吗?
一、激发求知欲
如何知道一锅汤的味道?
你知道其中蕴涵的道理吗?
根据这个道理,小华买火柴时怎么做才合理?
学习目标
1.了解抽样调查的概念并能区分全面调查和抽样调查;(重点)
2.了解样本、样本容量的概念及简单的抽样调查的方法.
二、展示目标和任务
问题 某中学共有2 000名学生,想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,请同学们想一想怎样调查.
如果采用全面调查的方式收集数据,不仅花费时间长,而且消耗的人力物力也非常大,你能找出既省时省力又能解决问题的办法么?
三、自主合作与交流
只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况,这种调查方法叫做抽样调查.
一、抽样调查
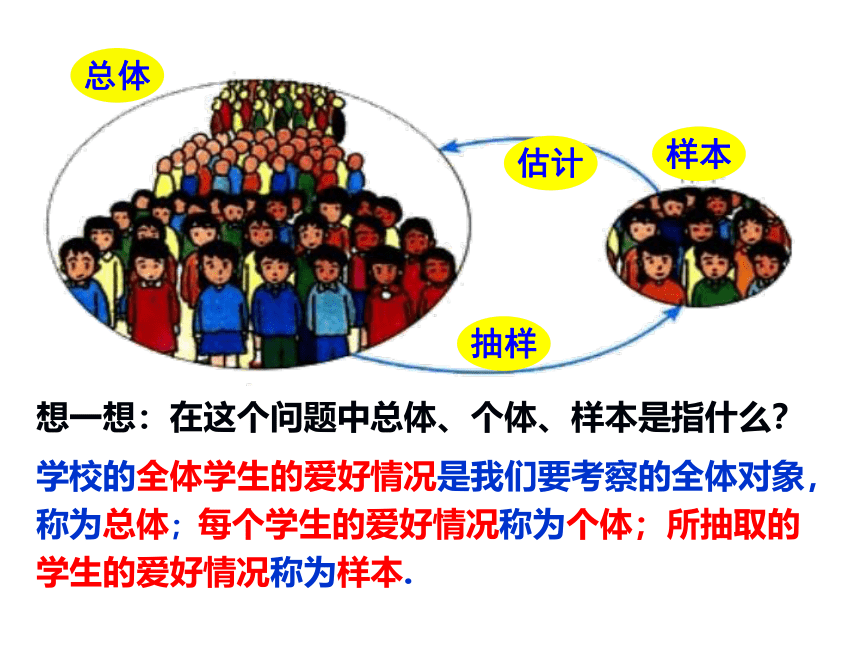
抽样调查的几个组成部分:
要考察的全体对象称为总体.
组成总体的每一个考察对象称为个体.
被抽取的那些个体组成一个样本.
样本中个体的数目称为样本容量.
抽样
总体
估计
样本
学校的全体学生的爱好情况是我们要考察的全体对象,称为总体;每个学生的爱好情况称为个体;所抽取的学生的爱好情况称为样本.
想一想:在这个问题中总体、个体、样本是指什么?
例 在一次考试中,考生有2万名.怎样才能既省时又省力的了解到这些考生的数学平均成绩呢?
?总体是________________;
?个体是________________;
?样本是________________;
?样本的容量是__ .
2万名考生数学成绩
其中每名考生的数学成绩
所抽取的500名考生的数学成绩
500
典例精析
2. 下列说法正确的是( )
A、样本中个体的数目叫总体;
B、考察对象的全体叫样本容量;
C、总体中的部分叫个体;
D、总体中抽出的一部分个体叫总体的一个样本.
D
思考:
前面问题中 全校有2000名学生,怎样选取调查人数,才能较准确地反映出全校学生的情况呢?
可以在全校2000名学生的注册学号中,随意抽取100个学号,调查这些学号对应的100名学生.
二、简单随机抽样
节目类型
划 记
人 数
A 新闻
正ー
6
B 体育
正正正正丅
22
C 动画
正正正正正
29
D 娱乐
正正正正正正正
38
E 戏曲
正
5
合 计
------------------
100
抽取100名学生最喜爱节目的人数统计表
百分比
6%
22%
29%
38%
5%
-------
全校的2000名学生,最喜欢哪类节目?对体育的喜爱约占几人?
节目类型
10
20
30
40
0
新闻
体育
动画
娱乐
戏曲
人数
6
22
29
38
5
条形图
扇形图
上面抽取样本的过程中,总体中的每一个个体都有相等的机会被抽到,像这样的抽样方法是一种简单的随机抽样.
为了使样本能较好地反映总体情况,除了有合适的样本容量外,抽取时还要尽量使每一个个体有相等的机会被抽到.
抽样调查是实际中经常采用的调查方式,如果抽取的样本得当,就能很好地反应总体情况,否则,抽样调查的结果会偏离总体情况.
采用调查部分对象的方式来收集数据, 根据部分来估计整体的情况, 叫做抽样调查.
所要考察对象的全体叫做总体.
从总体中所抽取的一部分个体叫做总体的一个样本.
总体中每一个考察对象叫做个体.
1.抽样调查:
2.总体:
3.个体:
4.样本:
5.样本容量:
样本中的个体的数目.
四、成果展示,教师点拨
抽样调查是一种方法,它只抽取了一部分对象进行调查,然后根据样本数据推断全体对象的情况。
如上面的例题,如果在抽取样本的过程中,总体的每一个个体都有相等的机会被抽到,这样的抽样方法就叫简单的随机抽样。
抽样调查是实际中经常采用的调查方式,如果抽取的样本得当,就能很好地反应总体情况,否则,抽样调查的结果会偏离总体情况。
注意:在抽样调查中抽取的样本要具有代表。
深化概念
全面调查 是通过调查总体的方式来收集数据,因而得到的调查结果比较精确;但可能要投入数十倍甚至更多的人力、物力和时间.
抽样调查 是通过调查样本的方式来收集数据,因而调查结果与总体的结果可能的一些误差,但投入少、操作方便,而且有时只能用抽样的方式去调查,比如要研究一批炮弹的杀伤半径,不可能把所有的炮弹都发射出去,可见合理的抽样调查不失为一种很好的选择.
比较概念
(1)当调查的对象个数较少,调查容易进行时,我们一般采用全面调查的方式进行。
(2)当调查的结果对调查对象具有破坏性时,或者会产生一定的危害性时,我们通常采用抽样调查的方式进行调查。
(3)当调查对象的个数较多,调查不易进行时,我们常采用抽样调查的方式进行调查。
(4)当调查的结果有特别要求时,或调查的结果有特殊意义时,如国家的人口普查,我们仍须采用全面调查的方式进行。
活用概念
1.下面几个问题,应该做全面调查还是抽样调查?
(1)要调查市场上某种食品添加剂是否符合国家标准;
(2)检测某城市的空气质量;
(3)调查一个村子所有家庭的收入;
(4)调查人们对保护环境的意识;
(5)调查一个班级中的学生对建立班级英语角的看法;
(6)调查人们对电影院放映的电影的热衷程度.
抽样调查
抽样调查
抽样调查
抽样调查
全面调查
全面调查
五、知识验证提升
3.想知道一批导弹的杀伤半径,采用什么调查方法?
为什么?
2.想知道一批灯泡的寿命采用什么调查方法?
4.某中学有520名学生参加升学考试从中随机抽取60名考生的数学成绩进行分析,在这个问题中:
总体是 ;
个体是 ;
样本是 ;
样本容量是 .
520名考生的升学考试数学成绩
每一个考生的升学考试数学成绩
抽取60名考生的升学考试数学成绩
60
5.为了了解一批电视机的使用寿命,从中抽取了10台
进行试验,对于这个问题,下列说法中正确的是( )
(A) 每台电视机的使用寿命是个体
(B) 一批电视机是总体
(C) 10台电视机是总体的一个样本
(D) 10台是样本容量
6. 2003年某区有15000名学生参加中考,为了考察他们的数学考试情况,评卷人从中抽取了800名考生的数学成绩进行统计,那么下列四个判断正确的是 ( ) (A)每名考生是个体
(B)这15000名考生的数学成绩是总体
(C)800名考生是总体的一个样本
(D)属于全面调查
A
B
答:⑴是抽样调查。
⑵总体是全校学生,个体是每一名同学,样本是座位在自己旁边的3名同学,样本容量为3。
7.为了解全校学生的平均身高,小明调查了座位在自己身边的3名同学,把他们身高的平均值作为全校学生平均身高的估计.
⑴小明的调查是抽样调查吗?
⑵如果是抽样调查,指出调查的总体、个体、样本和样本容量。
⑶这个调查结果能较好地反映总体的情况吗?
如果不能,请说明理由。
8.为了解全校学生的平均身高,小明调查了座位在自己身边的3名同学,把他们身高的平均值作为全校学生平均身高的估计.
⑴小明的调查是抽样调查吗?
⑵如果是抽样调查,指出调查的总体、个体、样本和样本容量。
⑶这个调查结果能较好地反映总体的情况吗?
如果不能,请说明理由。
⑶一般不能反映总体,一是样本容量太小,二是坐在一起的同学一般身高都比较接近,所以这样的选择的样本缺乏代表性。
1、宜采用全面调查
①. 总体中个体数目较少且研究问题要求情况真实、准确性较高时.
②. 调查工作较方便、没有破坏性.
③. 当调查的结果有特别要求时,或调查的结果有特殊意义时,如国家的人口普查,我们仍须的方式进行.
经验总结
注意:在抽样调查中抽取的样本要具有代表性。
2、宜采用抽样调查
①. 总体中个体数目较多,全面调查的工作量大,受 到客观条件限制,无法对所有个体进行调查.
② . 调查具有破坏性时,方式较好.
怎样估计鱼塘里有多少条鱼?
实验与探究
其近似比例关系为:
池塘里有标记鱼的数目 第二次捕捞出有标记鱼的数目
池塘中鱼的数目 第二次捕捞出鱼的数目
≈
具体做法是:
第一次捕捞出10条,把它们全部做上标记后放到池塘里,过一段时间进行第二次捕捞,若一共捕捞到100条鱼,其中2条鱼身上有标记,那么池塘里鱼的数目就可以通过近似比例关系,得到估计的数目。
1.你能举一个抽样调查的例子并能说出总体和样本分
别是什么吗?
2.利用抽样调查进行调查的好处是什么?
3.用样本的特征来估计总体的特征。
你能谈谈这堂课的收获吗?
好处:节省调查的人力和物力,
不足之处:与实际可能存在误差.
课堂小结
10.1 统计调查
2 抽样调查
一天,爸爸叫儿子小华去买一盒火柴.临出门前,爸爸嘱咐儿子要买能划燃的火柴.小华拿着钱出门了,过了好一会儿,小华才回到家.
“火柴能划燃吗?”爸爸问.
“都能划燃.”
“你这么肯定?”
小华递过一盒划过的火柴,兴奋地说:“我每根都试过啦.”
思考:得到火柴能否划燃的信息准确吗? 这样做好吗?
小华这样买火柴对吗?
一、激发求知欲
如何知道一锅汤的味道?
你知道其中蕴涵的道理吗?
根据这个道理,小华买火柴时怎么做才合理?
学习目标
1.了解抽样调查的概念并能区分全面调查和抽样调查;(重点)
2.了解样本、样本容量的概念及简单的抽样调查的方法.
二、展示目标和任务
问题 某中学共有2 000名学生,想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,请同学们想一想怎样调查.
如果采用全面调查的方式收集数据,不仅花费时间长,而且消耗的人力物力也非常大,你能找出既省时省力又能解决问题的办法么?
三、自主合作与交流
只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况,这种调查方法叫做抽样调查.
一、抽样调查
抽样调查的几个组成部分:
要考察的全体对象称为总体.
组成总体的每一个考察对象称为个体.
被抽取的那些个体组成一个样本.
样本中个体的数目称为样本容量.
抽样
总体
估计
样本
学校的全体学生的爱好情况是我们要考察的全体对象,称为总体;每个学生的爱好情况称为个体;所抽取的学生的爱好情况称为样本.
想一想:在这个问题中总体、个体、样本是指什么?
例 在一次考试中,考生有2万名.怎样才能既省时又省力的了解到这些考生的数学平均成绩呢?
?总体是________________;
?个体是________________;
?样本是________________;
?样本的容量是__ .
2万名考生数学成绩
其中每名考生的数学成绩
所抽取的500名考生的数学成绩
500
典例精析
2. 下列说法正确的是( )
A、样本中个体的数目叫总体;
B、考察对象的全体叫样本容量;
C、总体中的部分叫个体;
D、总体中抽出的一部分个体叫总体的一个样本.
D
思考:
前面问题中 全校有2000名学生,怎样选取调查人数,才能较准确地反映出全校学生的情况呢?
可以在全校2000名学生的注册学号中,随意抽取100个学号,调查这些学号对应的100名学生.
二、简单随机抽样
节目类型
划 记
人 数
A 新闻
正ー
6
B 体育
正正正正丅
22
C 动画
正正正正正
29
D 娱乐
正正正正正正正
38
E 戏曲
正
5
合 计
------------------
100
抽取100名学生最喜爱节目的人数统计表
百分比
6%
22%
29%
38%
5%
-------
全校的2000名学生,最喜欢哪类节目?对体育的喜爱约占几人?
节目类型
10
20
30
40
0
新闻
体育
动画
娱乐
戏曲
人数
6
22
29
38
5
条形图
扇形图
上面抽取样本的过程中,总体中的每一个个体都有相等的机会被抽到,像这样的抽样方法是一种简单的随机抽样.
为了使样本能较好地反映总体情况,除了有合适的样本容量外,抽取时还要尽量使每一个个体有相等的机会被抽到.
抽样调查是实际中经常采用的调查方式,如果抽取的样本得当,就能很好地反应总体情况,否则,抽样调查的结果会偏离总体情况.
采用调查部分对象的方式来收集数据, 根据部分来估计整体的情况, 叫做抽样调查.
所要考察对象的全体叫做总体.
从总体中所抽取的一部分个体叫做总体的一个样本.
总体中每一个考察对象叫做个体.
1.抽样调查:
2.总体:
3.个体:
4.样本:
5.样本容量:
样本中的个体的数目.
四、成果展示,教师点拨
抽样调查是一种方法,它只抽取了一部分对象进行调查,然后根据样本数据推断全体对象的情况。
如上面的例题,如果在抽取样本的过程中,总体的每一个个体都有相等的机会被抽到,这样的抽样方法就叫简单的随机抽样。
抽样调查是实际中经常采用的调查方式,如果抽取的样本得当,就能很好地反应总体情况,否则,抽样调查的结果会偏离总体情况。
注意:在抽样调查中抽取的样本要具有代表。
深化概念
全面调查 是通过调查总体的方式来收集数据,因而得到的调查结果比较精确;但可能要投入数十倍甚至更多的人力、物力和时间.
抽样调查 是通过调查样本的方式来收集数据,因而调查结果与总体的结果可能的一些误差,但投入少、操作方便,而且有时只能用抽样的方式去调查,比如要研究一批炮弹的杀伤半径,不可能把所有的炮弹都发射出去,可见合理的抽样调查不失为一种很好的选择.
比较概念
(1)当调查的对象个数较少,调查容易进行时,我们一般采用全面调查的方式进行。
(2)当调查的结果对调查对象具有破坏性时,或者会产生一定的危害性时,我们通常采用抽样调查的方式进行调查。
(3)当调查对象的个数较多,调查不易进行时,我们常采用抽样调查的方式进行调查。
(4)当调查的结果有特别要求时,或调查的结果有特殊意义时,如国家的人口普查,我们仍须采用全面调查的方式进行。
活用概念
1.下面几个问题,应该做全面调查还是抽样调查?
(1)要调查市场上某种食品添加剂是否符合国家标准;
(2)检测某城市的空气质量;
(3)调查一个村子所有家庭的收入;
(4)调查人们对保护环境的意识;
(5)调查一个班级中的学生对建立班级英语角的看法;
(6)调查人们对电影院放映的电影的热衷程度.
抽样调查
抽样调查
抽样调查
抽样调查
全面调查
全面调查
五、知识验证提升
3.想知道一批导弹的杀伤半径,采用什么调查方法?
为什么?
2.想知道一批灯泡的寿命采用什么调查方法?
4.某中学有520名学生参加升学考试从中随机抽取60名考生的数学成绩进行分析,在这个问题中:
总体是 ;
个体是 ;
样本是 ;
样本容量是 .
520名考生的升学考试数学成绩
每一个考生的升学考试数学成绩
抽取60名考生的升学考试数学成绩
60
5.为了了解一批电视机的使用寿命,从中抽取了10台
进行试验,对于这个问题,下列说法中正确的是( )
(A) 每台电视机的使用寿命是个体
(B) 一批电视机是总体
(C) 10台电视机是总体的一个样本
(D) 10台是样本容量
6. 2003年某区有15000名学生参加中考,为了考察他们的数学考试情况,评卷人从中抽取了800名考生的数学成绩进行统计,那么下列四个判断正确的是 ( ) (A)每名考生是个体
(B)这15000名考生的数学成绩是总体
(C)800名考生是总体的一个样本
(D)属于全面调查
A
B
答:⑴是抽样调查。
⑵总体是全校学生,个体是每一名同学,样本是座位在自己旁边的3名同学,样本容量为3。
7.为了解全校学生的平均身高,小明调查了座位在自己身边的3名同学,把他们身高的平均值作为全校学生平均身高的估计.
⑴小明的调查是抽样调查吗?
⑵如果是抽样调查,指出调查的总体、个体、样本和样本容量。
⑶这个调查结果能较好地反映总体的情况吗?
如果不能,请说明理由。
8.为了解全校学生的平均身高,小明调查了座位在自己身边的3名同学,把他们身高的平均值作为全校学生平均身高的估计.
⑴小明的调查是抽样调查吗?
⑵如果是抽样调查,指出调查的总体、个体、样本和样本容量。
⑶这个调查结果能较好地反映总体的情况吗?
如果不能,请说明理由。
⑶一般不能反映总体,一是样本容量太小,二是坐在一起的同学一般身高都比较接近,所以这样的选择的样本缺乏代表性。
1、宜采用全面调查
①. 总体中个体数目较少且研究问题要求情况真实、准确性较高时.
②. 调查工作较方便、没有破坏性.
③. 当调查的结果有特别要求时,或调查的结果有特殊意义时,如国家的人口普查,我们仍须的方式进行.
经验总结
注意:在抽样调查中抽取的样本要具有代表性。
2、宜采用抽样调查
①. 总体中个体数目较多,全面调查的工作量大,受 到客观条件限制,无法对所有个体进行调查.
② . 调查具有破坏性时,方式较好.
怎样估计鱼塘里有多少条鱼?
实验与探究
其近似比例关系为:
池塘里有标记鱼的数目 第二次捕捞出有标记鱼的数目
池塘中鱼的数目 第二次捕捞出鱼的数目
≈
具体做法是:
第一次捕捞出10条,把它们全部做上标记后放到池塘里,过一段时间进行第二次捕捞,若一共捕捞到100条鱼,其中2条鱼身上有标记,那么池塘里鱼的数目就可以通过近似比例关系,得到估计的数目。
1.你能举一个抽样调查的例子并能说出总体和样本分
别是什么吗?
2.利用抽样调查进行调查的好处是什么?
3.用样本的特征来估计总体的特征。
你能谈谈这堂课的收获吗?
好处:节省调查的人力和物力,
不足之处:与实际可能存在误差.
课堂小结
