人教版七年级下册课件 第六章《实数》复习(共24张PPT)
文档属性
| 名称 | 人教版七年级下册课件 第六章《实数》复习(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 17:47:09 | ||
图片预览




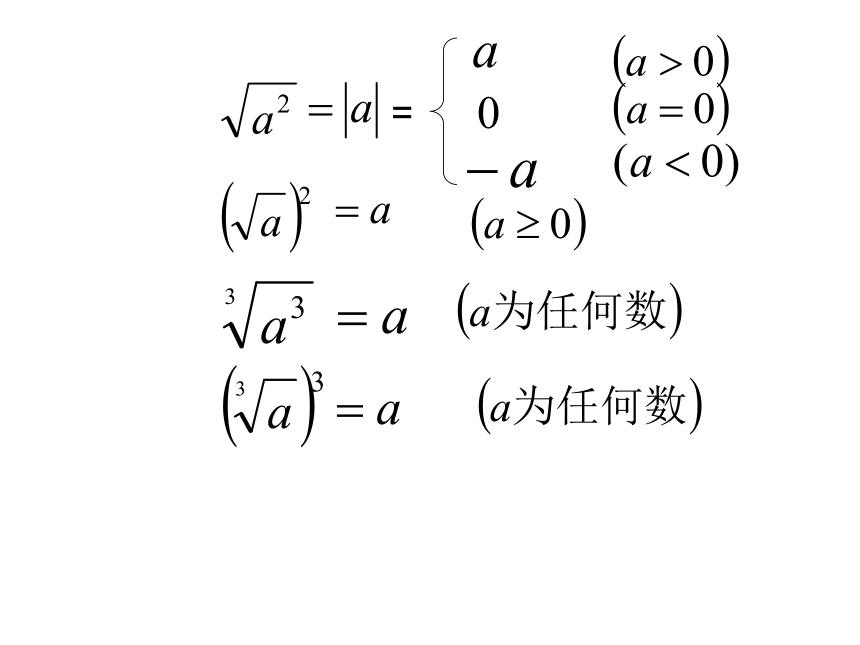

文档简介
第六章实数的复习
定义
一般地,如果一个正数 x 的平方等于 a(x2 = a),那么这个正数 x 就叫做 a 的
算术平方根
a 的算术平方根记作
读作
“ 根号a ”
根号
被开方数
规定:0的算术平方根等于0
如102 = 100
则100的算术平方根
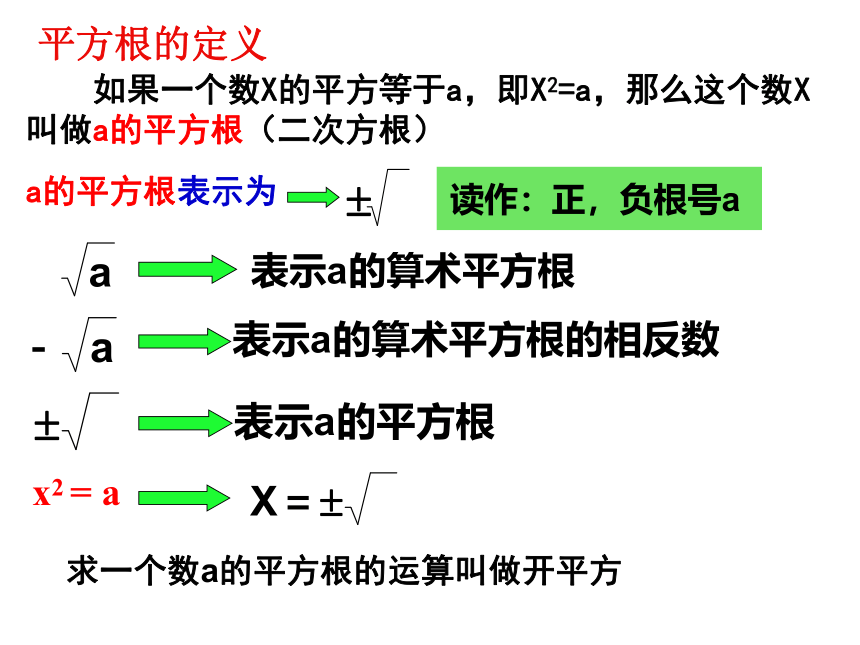
如果一个数X的平方等于a,即X2=a,那么这个数X叫做a的平方根(二次方根)
a的平方根表示为
x2 = a
求一个数a的平方根的运算叫做开平方
平方根的定义
平方根的性质:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
若一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根。
1、什么是立方根?
2、正数的立方根是一个______,负数的立方根是一个_______,0 的立方根是____;立方根是它本身的数是______.平方根是它本身的数是__算术平方根是它本身的数是______.
正数
负数
0
1、-1、0
0
0、1
正数有立方根吗?如果有,有几个?
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
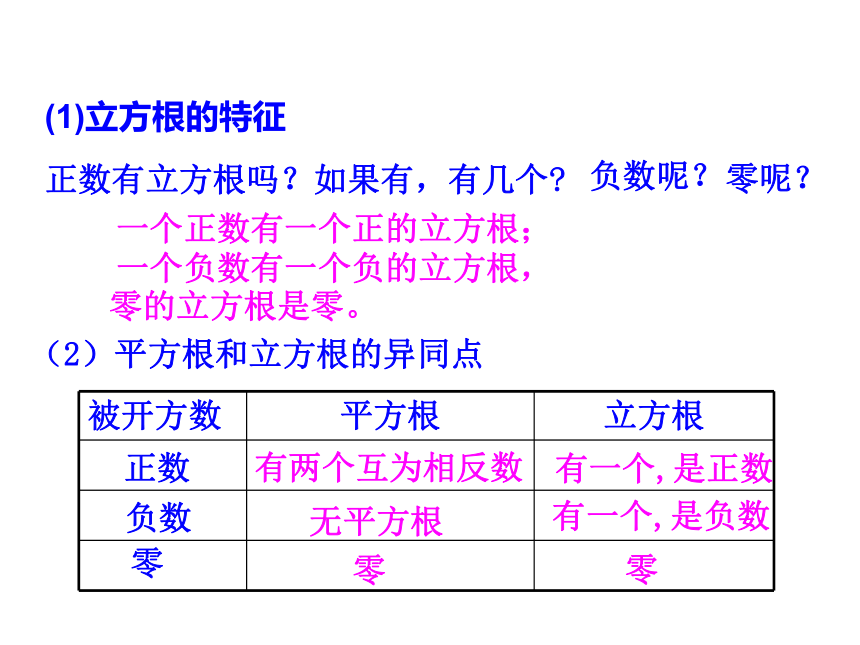
(1)立方根的特征
(2)平方根和立方根的异同点
被开方数
平方根
立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
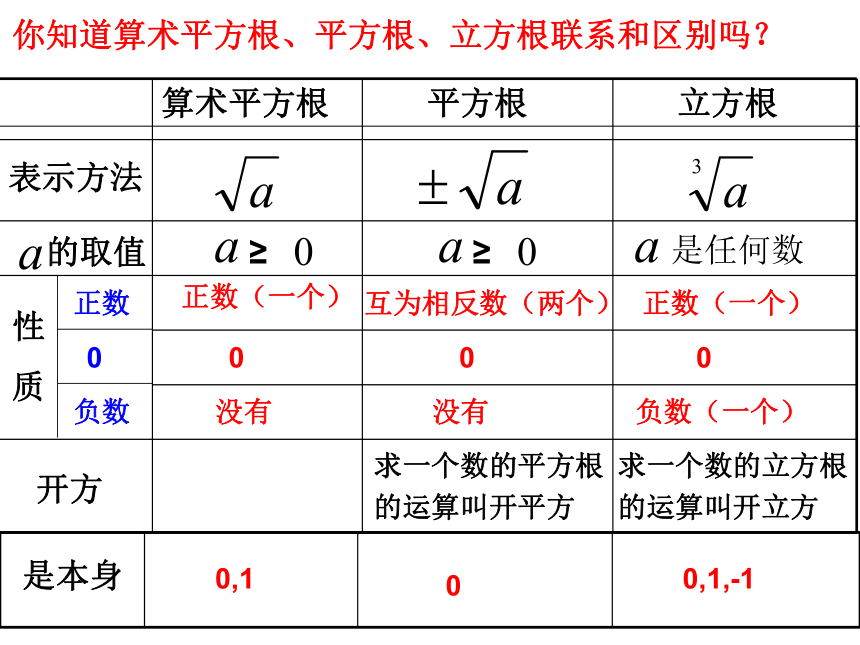
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
=
2.说出下列各数的立方根:
1.说出下列各数的平方根和算术平方根:
(1)169
(3)64/25
(4)100
(2)0.16
(5)25/9
3.说出下列各式的值:
练习:
;
解:原式=-a+a
=0
解:原式=n-m+n-m
=2n-2m
无限不循环的小数 叫做无理数.
在进行实数的运算时,有理数的运算法则及运算性质同样适用。
有理数和无理数统称实数.
实数与 上的点是一一对应的
在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意
义完全一样
数轴
实数
有理数
无理数
正整数
0
负整数
正分数
负分数
分数
整数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
练习:
1、判断下列说法是否正确:
(1)实数不是有理数就是无理数。 ( )
(2)无限小数都是无理数。 ( )
(3)无理数都是无限小数。 ( )
(4)带根号的数都是无理数。 ( )
(5)两个无理数之和一定是无理数.( )
(6)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
2.把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
不要遗漏
3.解方程:
当方程中出现平方时,若有解,
一般都有两个解
当方程中出现立方时,一般都有一个解
(1).
解:
(2).
解:
知识提高
1、已知
,
(3)0.03的平方根约为 ;
(4)若
2、已知
,
,
,求(1)
(2)3000的立方根约为 ;
(3)
,则
17.32
0.5477
0.1732
3000
0.6694
14.42
30000
5、已知
的小数部分为m,
,
的小数部分为n
6、计算:
1
解:原式=1.2+0.4+1-2
=0.6
解:原式=3+5-1+4
=11
强化运用
1、下列说法正确的是( )
A、
B 表示6的算术平方根的相反数
C、 任何数都有平方根 D、
一定没有平方根
B
-5
x≤0
X为任何实数
5、已知等腰三角形的两边长
满足
,求三角形的周长
解:由题意得:
2x-1≥0
1-2x≥0
{
{
解得:
,y=1
∴2x+3y=4
解:由题意,得
2a-3b+5=0
2a-3b-13=0
{
{
解得:
a=2
b=3
所以等腰三角形的三边为2,2,3或2,3,3
所以,三角形的周长为7或8
6、已知
,求
的值。
7、已知
,求 y-x的算术
平方根
解:由题意得:
{
{
a-4≥0
解得a≥4
∴ a-3+
∴a-4=9
∴a=13
解:由题意,得:
X-2≥0
2-x≥0
解得:
x≥2
x≤2
∴x=2
当x=2时,y=3
解:由题意,得
解:由题意,得:
{
{
{
{
X-2y-3=0
2x-3y-5=0
解得
x=1
y=-1
x=8
y-1=0
z-3=0
解得:
x=8
y=1
z=3
掌握规律
10
定义
一般地,如果一个正数 x 的平方等于 a(x2 = a),那么这个正数 x 就叫做 a 的
算术平方根
a 的算术平方根记作
读作
“ 根号a ”
根号
被开方数
规定:0的算术平方根等于0
如102 = 100
则100的算术平方根
如果一个数X的平方等于a,即X2=a,那么这个数X叫做a的平方根(二次方根)
a的平方根表示为
x2 = a
求一个数a的平方根的运算叫做开平方
平方根的定义
平方根的性质:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。
若一个数的立方等于a,那么这个数叫做 a 的立方根或三次方根。
1、什么是立方根?
2、正数的立方根是一个______,负数的立方根是一个_______,0 的立方根是____;立方根是它本身的数是______.平方根是它本身的数是__算术平方根是它本身的数是______.
正数
负数
0
1、-1、0
0
0、1
正数有立方根吗?如果有,有几个?
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
(1)立方根的特征
(2)平方根和立方根的异同点
被开方数
平方根
立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身
0,1
0
0,1,-1
=
2.说出下列各数的立方根:
1.说出下列各数的平方根和算术平方根:
(1)169
(3)64/25
(4)100
(2)0.16
(5)25/9
3.说出下列各式的值:
练习:
;
解:原式=-a+a
=0
解:原式=n-m+n-m
=2n-2m
无限不循环的小数 叫做无理数.
在进行实数的运算时,有理数的运算法则及运算性质同样适用。
有理数和无理数统称实数.
实数与 上的点是一一对应的
在实数范围内,相反数、倒数、绝对值的意义
和有理数范围内的相反数、倒数、绝对值的意
义完全一样
数轴
实数
有理数
无理数
正整数
0
负整数
正分数
负分数
分数
整数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但不循环的无限小数
练习:
1、判断下列说法是否正确:
(1)实数不是有理数就是无理数。 ( )
(2)无限小数都是无理数。 ( )
(3)无理数都是无限小数。 ( )
(4)带根号的数都是无理数。 ( )
(5)两个无理数之和一定是无理数.( )
(6)所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
2.把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
不要遗漏
3.解方程:
当方程中出现平方时,若有解,
一般都有两个解
当方程中出现立方时,一般都有一个解
(1).
解:
(2).
解:
知识提高
1、已知
,
(3)0.03的平方根约为 ;
(4)若
2、已知
,
,
,求(1)
(2)3000的立方根约为 ;
(3)
,则
17.32
0.5477
0.1732
3000
0.6694
14.42
30000
5、已知
的小数部分为m,
,
的小数部分为n
6、计算:
1
解:原式=1.2+0.4+1-2
=0.6
解:原式=3+5-1+4
=11
强化运用
1、下列说法正确的是( )
A、
B 表示6的算术平方根的相反数
C、 任何数都有平方根 D、
一定没有平方根
B
-5
x≤0
X为任何实数
5、已知等腰三角形的两边长
满足
,求三角形的周长
解:由题意得:
2x-1≥0
1-2x≥0
{
{
解得:
,y=1
∴2x+3y=4
解:由题意,得
2a-3b+5=0
2a-3b-13=0
{
{
解得:
a=2
b=3
所以等腰三角形的三边为2,2,3或2,3,3
所以,三角形的周长为7或8
6、已知
,求
的值。
7、已知
,求 y-x的算术
平方根
解:由题意得:
{
{
a-4≥0
解得a≥4
∴ a-3+
∴a-4=9
∴a=13
解:由题意,得:
X-2≥0
2-x≥0
解得:
x≥2
x≤2
∴x=2
当x=2时,y=3
解:由题意,得
解:由题意,得:
{
{
{
{
X-2y-3=0
2x-3y-5=0
解得
x=1
y=-1
x=8
y-1=0
z-3=0
解得:
x=8
y=1
z=3
掌握规律
10
