人教版七年级下册课件 第七章 平面直角坐标系小结(共19张PPT)
文档属性
| 名称 | 人教版七年级下册课件 第七章 平面直角坐标系小结(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 626.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 17:48:37 | ||
图片预览





文档简介
小结与复习
第七章 平面直角坐标系
一、复习目标
1、理解平面直角坐标系的意义,熟练掌握各象限内点的坐标特征。掌握一些特殊点的坐标求法。
2.能建立适当的平面直角坐标系描述物体的位置.在同一直角坐标系中,感受图形变换后点的坐标的变化。
3.在平面直角坐标系中,能用坐标表示平移变换。
4、进一步体会数形结合的数学思想。
二、情感目标及价值观:
敢于面对数学活动中的困难,有独立克服困难和应用知识解决问题的成功经验,有学好数学的自信心。
三、复习重点:
利用本节知识解决各类问题。
四、复习难点:
1、特殊点的坐标求法。
2、利用平面直角坐标系解决实际问题。
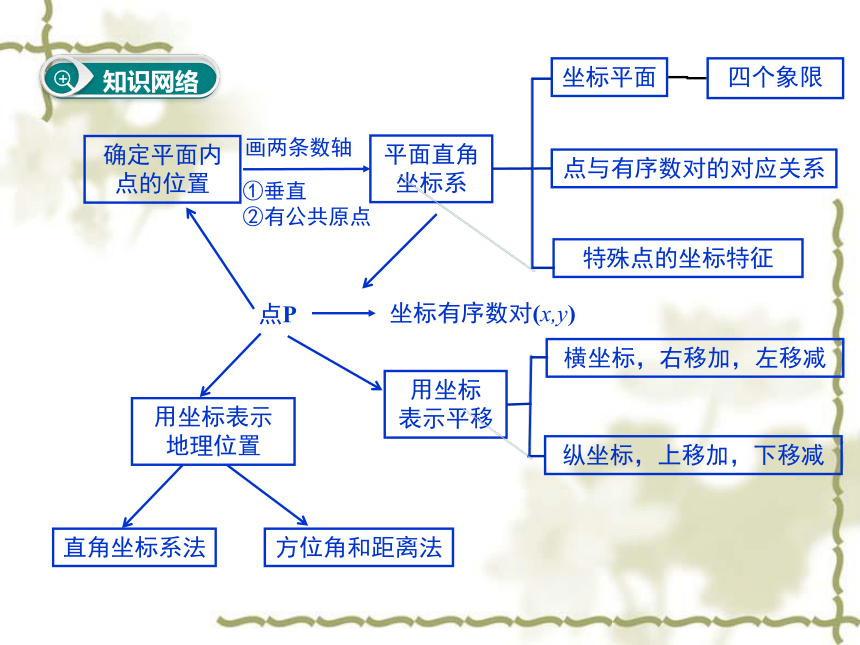
知识网络
确定平面内点的位置
平面直角
坐标系
坐标平面
四个象限
点与有序数对的对应关系
特殊点的坐标特征
点P
画两条数轴
①垂直
②有公共原点
坐标有序数对(x,y)
用坐标
表示平移
横坐标,右移加,左移减
纵坐标,上移加,下移减
用坐标表示
地理位置
直角坐标系法
方位角和距离法
专题复习
【例1】已知点A(-3+a,2a+9)在第二象限,且到x轴的距离为5,则点a的值是 .
-2
专题一 平面直角坐标系与点的坐标
【归纳拓展】
1.一、三象限内点的横、纵坐标同号;
2.二、四象限内点的横、纵坐标异号;
3.平面内点到x轴的距离是它的纵坐标的绝对值,到y轴的
距离是它横坐标的绝对值;
4.平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线上的点的横坐标相同.
【迁移应用1】
(1)已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则
m的值为 .
-1
(2)已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则
点B的坐标是 .
(2,2)或(-2,2)
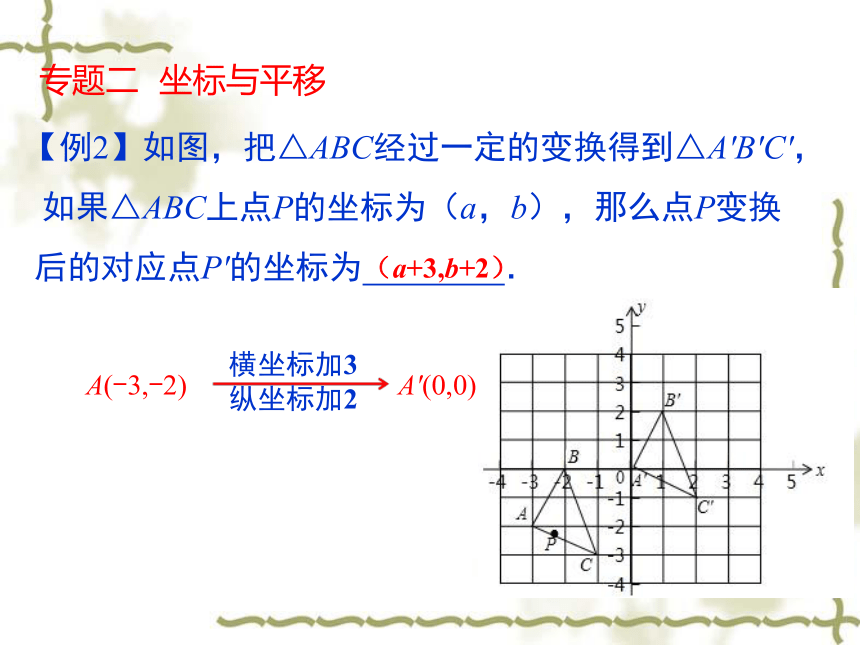
【例2】如图,把△ABC经过一定的变换得到△A′B′C′,
如果△ABC上点P的坐标为(a,b),那么点P变换
后的对应点P′的坐标为 .
(a+3,b+2)
A(-3,-2)
A′(0,0)
横坐标加3
纵坐标加2
专题二 坐标与平移
【归纳拓展】为了更加直观、便捷地表示一些图形,或具体事物的位置,通常采用坐标方法.观察一个图形进行了怎样的平移,关键是抓住对应点进行怎样的平移.
【迁移应用2】
将点P(-3,y)向下平移3个单位,再向左平移2个单位得到点Q(x,-1),则xy= .
-10
【例3】(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个
单位长度,再向下平移4个
单位长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A
B
C
A(0,2)
B(4,3)
C(3,0)
5.5
专题三 平移作图及求坐标系中的几何图形面积
【归纳拓展】在坐标系中求图形的面积应从两方面去把握:(一)通常用割或补的方法将要求图形转让化为一些特殊的图
形,去间接计算面积.
(二)需要将已知点的坐标转化为线段的长度,以满足求面积
的需要.
【迁移应用3】
已知直角三角形ABC的直角边BC=AC,
且B(3,2),C(3,-2),求点A的坐标及△ABC的面积.
A
B
C
O
x
y
答案:A点坐标为(-1,-2),△ABC面积是8.
课堂小结
平面直角坐标系
概念及有关知识
坐标方法
的应用
有序数对(a,b)
坐标系画法(坐标、x轴和y轴、象限)
平面上的点
点的坐标
表示地理位置(选、建、标、写)
表示平移
课后训练
1.点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的
坐标是 .
2.点P(a-1,a2-9)在x轴负半轴上,则P点的坐标
是 .
(3 ,-2)
(-4 ,0)
3.点A(2,3)到x轴的距离为 ;点B(-4,0)到y
轴的距离为 ;点C到x轴的距离为1,到y轴的
距离为3,且在第三象限,则C点坐标是 .
3个单位
4个单位
(-3 ,-1)
4.直角坐标系中,在y轴上有一点P ,且OP=5,则
P的坐标为 .
(0 ,5)或(0 ,-5)
5.已知A(1,4),B(-4,0),C(2,0),则△ABC的面积是 .
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
(1)点P的坐标是(2,-3),则点P在第 象限;
四
一或三
(3)若点P(x,y)的坐标满足 xy﹤0,且在x轴上方,则点P在第 象限;
二
巩固练习1:由坐标找象限。
温馨提示:判断点的位置,关键抓住象限内点的 坐标的符号特征.
(2)若点P(x,y)的坐标满足xy﹥0,
则点P在第 象限;
(4)若点A的坐标为(a2+1, -2–b2),则点A在第____象限.
四
巩固练习2:坐标轴上点的坐标
(1)点P(m+2,m-1)在x轴上,则点P的坐标是 .
( 3, 0 )
(2)点P(m+2,m-1)在y轴上,则点P的坐标是 .
( 0, -3 )
(3)点P(x,y)满足 xy=0,
则点P在 .
x 轴上 或 y 轴上
注意: 1. x轴上的点的纵坐标为0,表示为(x,0),
2. y轴上的点的横坐标为0, 表示为(0,y)。
原点(0,0)既在x轴上,又在y轴上。
4. 特殊位置的点的坐标特点:
(1)第一、三象限夹角平分线上的点:
横 纵坐标 。 第二、四象限夹角平分线上的点:横纵坐标 。
(2)与x轴平行(或与y轴垂直)的直线上的点: 坐标都相同 。与y轴平行(或与x轴垂直)的直线上的点: 坐标都相同。
相同
互为相反数
横
纵
(2).已知点A(2a+1,2+a)在第二象限的平分线上,试求A的坐标。
(1).已知点A(2,y ),点B(x ,5 ),点A、B在一、三象限的角平分线上, 则x =____,y =____;
5
2
A( -1, ,1 )
(1). 已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为 。
-1
(2). 已知点A(m,-2)、点B(3,m-1),且直线AB∥y轴,则m的值为 。
3
(1). 点( x, y )到 x 轴的距离是
(2). 点( x, y )到 y 轴的距离是
(1).若点A的坐标是(- 3, 5),则它到x轴的距离是 ,到y轴的距离是 .
5
3
(2).点P到x轴、y轴的距离分别是2,1,则点P的坐标可能为 .
(1,2)、 (-1,2)、(-1,-2) 、(1,-2).
巩固练习:
第七章 平面直角坐标系
一、复习目标
1、理解平面直角坐标系的意义,熟练掌握各象限内点的坐标特征。掌握一些特殊点的坐标求法。
2.能建立适当的平面直角坐标系描述物体的位置.在同一直角坐标系中,感受图形变换后点的坐标的变化。
3.在平面直角坐标系中,能用坐标表示平移变换。
4、进一步体会数形结合的数学思想。
二、情感目标及价值观:
敢于面对数学活动中的困难,有独立克服困难和应用知识解决问题的成功经验,有学好数学的自信心。
三、复习重点:
利用本节知识解决各类问题。
四、复习难点:
1、特殊点的坐标求法。
2、利用平面直角坐标系解决实际问题。
知识网络
确定平面内点的位置
平面直角
坐标系
坐标平面
四个象限
点与有序数对的对应关系
特殊点的坐标特征
点P
画两条数轴
①垂直
②有公共原点
坐标有序数对(x,y)
用坐标
表示平移
横坐标,右移加,左移减
纵坐标,上移加,下移减
用坐标表示
地理位置
直角坐标系法
方位角和距离法
专题复习
【例1】已知点A(-3+a,2a+9)在第二象限,且到x轴的距离为5,则点a的值是 .
-2
专题一 平面直角坐标系与点的坐标
【归纳拓展】
1.一、三象限内点的横、纵坐标同号;
2.二、四象限内点的横、纵坐标异号;
3.平面内点到x轴的距离是它的纵坐标的绝对值,到y轴的
距离是它横坐标的绝对值;
4.平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线上的点的横坐标相同.
【迁移应用1】
(1)已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则
m的值为 .
-1
(2)已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则
点B的坐标是 .
(2,2)或(-2,2)
【例2】如图,把△ABC经过一定的变换得到△A′B′C′,
如果△ABC上点P的坐标为(a,b),那么点P变换
后的对应点P′的坐标为 .
(a+3,b+2)
A(-3,-2)
A′(0,0)
横坐标加3
纵坐标加2
专题二 坐标与平移
【归纳拓展】为了更加直观、便捷地表示一些图形,或具体事物的位置,通常采用坐标方法.观察一个图形进行了怎样的平移,关键是抓住对应点进行怎样的平移.
【迁移应用2】
将点P(-3,y)向下平移3个单位,再向左平移2个单位得到点Q(x,-1),则xy= .
-10
【例3】(1)写出三角形ABC的各个顶点的坐标;
(2)试求出三角形ABC的面积;
(3)将三角形先向左平移5个
单位长度,再向下平移4个
单位长度,画出平移后的图形.
x
y
0
1
1
2
3
4
5
2
3
4
5
-1
-2
-3
-4
-1
-2
-3
-4
-5
A
B
C
A(0,2)
B(4,3)
C(3,0)
5.5
专题三 平移作图及求坐标系中的几何图形面积
【归纳拓展】在坐标系中求图形的面积应从两方面去把握:(一)通常用割或补的方法将要求图形转让化为一些特殊的图
形,去间接计算面积.
(二)需要将已知点的坐标转化为线段的长度,以满足求面积
的需要.
【迁移应用3】
已知直角三角形ABC的直角边BC=AC,
且B(3,2),C(3,-2),求点A的坐标及△ABC的面积.
A
B
C
O
x
y
答案:A点坐标为(-1,-2),△ABC面积是8.
课堂小结
平面直角坐标系
概念及有关知识
坐标方法
的应用
有序数对(a,b)
坐标系画法(坐标、x轴和y轴、象限)
平面上的点
点的坐标
表示地理位置(选、建、标、写)
表示平移
课后训练
1.点P(x,y)在第四象限,且|x|=3,|y|=2,则P点的
坐标是 .
2.点P(a-1,a2-9)在x轴负半轴上,则P点的坐标
是 .
(3 ,-2)
(-4 ,0)
3.点A(2,3)到x轴的距离为 ;点B(-4,0)到y
轴的距离为 ;点C到x轴的距离为1,到y轴的
距离为3,且在第三象限,则C点坐标是 .
3个单位
4个单位
(-3 ,-1)
4.直角坐标系中,在y轴上有一点P ,且OP=5,则
P的坐标为 .
(0 ,5)或(0 ,-5)
5.已知A(1,4),B(-4,0),C(2,0),则△ABC的面积是 .
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
12
(1)点P的坐标是(2,-3),则点P在第 象限;
四
一或三
(3)若点P(x,y)的坐标满足 xy﹤0,且在x轴上方,则点P在第 象限;
二
巩固练习1:由坐标找象限。
温馨提示:判断点的位置,关键抓住象限内点的 坐标的符号特征.
(2)若点P(x,y)的坐标满足xy﹥0,
则点P在第 象限;
(4)若点A的坐标为(a2+1, -2–b2),则点A在第____象限.
四
巩固练习2:坐标轴上点的坐标
(1)点P(m+2,m-1)在x轴上,则点P的坐标是 .
( 3, 0 )
(2)点P(m+2,m-1)在y轴上,则点P的坐标是 .
( 0, -3 )
(3)点P(x,y)满足 xy=0,
则点P在 .
x 轴上 或 y 轴上
注意: 1. x轴上的点的纵坐标为0,表示为(x,0),
2. y轴上的点的横坐标为0, 表示为(0,y)。
原点(0,0)既在x轴上,又在y轴上。
4. 特殊位置的点的坐标特点:
(1)第一、三象限夹角平分线上的点:
横 纵坐标 。 第二、四象限夹角平分线上的点:横纵坐标 。
(2)与x轴平行(或与y轴垂直)的直线上的点: 坐标都相同 。与y轴平行(或与x轴垂直)的直线上的点: 坐标都相同。
相同
互为相反数
横
纵
(2).已知点A(2a+1,2+a)在第二象限的平分线上,试求A的坐标。
(1).已知点A(2,y ),点B(x ,5 ),点A、B在一、三象限的角平分线上, 则x =____,y =____;
5
2
A( -1, ,1 )
(1). 已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为 。
-1
(2). 已知点A(m,-2)、点B(3,m-1),且直线AB∥y轴,则m的值为 。
3
(1). 点( x, y )到 x 轴的距离是
(2). 点( x, y )到 y 轴的距离是
(1).若点A的坐标是(- 3, 5),则它到x轴的距离是 ,到y轴的距离是 .
5
3
(2).点P到x轴、y轴的距离分别是2,1,则点P的坐标可能为 .
(1,2)、 (-1,2)、(-1,-2) 、(1,-2).
巩固练习:
