人教版七年级下册数学6.1算术平方根课件(共18张PPT)
文档属性
| 名称 | 人教版七年级下册数学6.1算术平方根课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第 六 章 实 数
—算术平方根
学校要举行美术作品比赛,小欧很
高兴,他想裁出一块面积为25dm 的正
方形画布,画上自己的得意之作参比
赛,这块正方形画布的边长应取多少?
2
5 dm
身边小事
§6.1 平方根
因为 =25
5
2
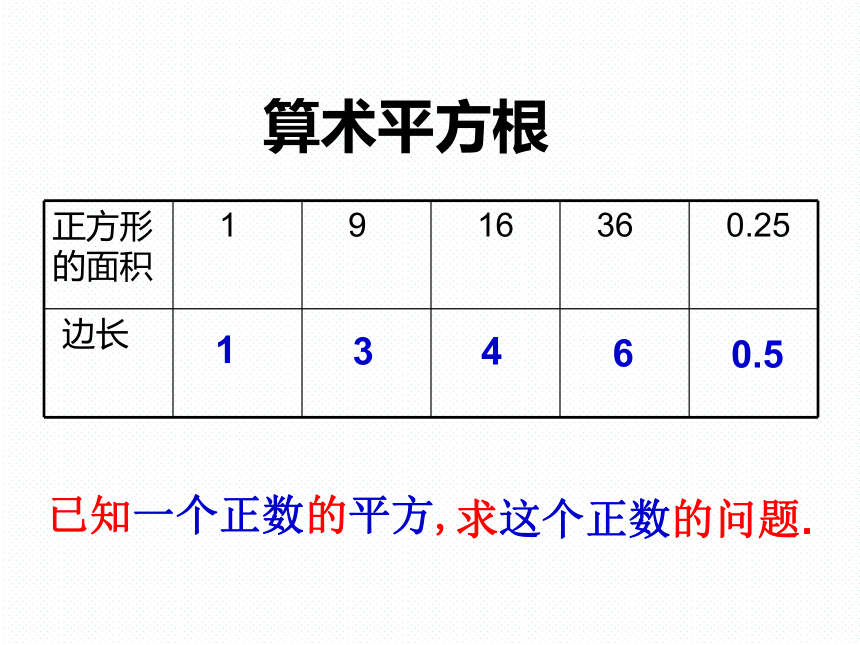
正方形的面积 1 9 16 36 0.25
边长
1
3
4
6
0.5
已知一个正数的平方,
算术平方根
求这个正数的问题.
如果一个正数 的平方等于 ,
x
a
x
一个正数
概念引入
那么5叫做25的算术平方根;
那么10叫做100的算术平方根;
a
x
即 = ,
2
那么这个正数 叫做 的
x
a
算术平方根.
一般地,
x
a
2
x
=
a
a
算术平方根
★ 说出下列各数的算术平方根:
9
4
3
的算术平方根是 3;
的算术平方根是 2,
的算术平方根记为
a
a,
读作:“ 根号 ”,
a
a
叫做被开方数,
x
=
a
,
9
=
4
=
规定:0的算术平方根是0,
即
0
=0.
10 =100,
2
象5 =25,
2
3
的算术平方根是
算术平方根的概念及性质
如果一个正数 的平方等于 ,
x
a
a
x
一个正数
a
x
即 = ,
2
那么这个正数 叫做 的
x
a
算术平方根.
一般地,
x
2
x
=
a
a
算术平方根
的算术平方根记为
a
a,
读作:“ 根号 ”,
a
a
叫做被开方数,
x
=
a
,
规定:0的算术平方根事0,
即
0
=0.
试一试
1.求下列各数的算术平方根:
解: (1)
因为 =100,
10
2
(5) 3
2
所以100的算术平方根为10,
即 =10.
100
(1) 100; (2) 1; (3) 0 ; (4) ;
64
49
(6) -4
(6)
因为没有一个数的平方可能是负数,
所以-4没有算术平方根.
≥
0
算术平方根的非负双重性.
对于 :
a
0
≥
a
a
}
例、下列各式中哪些有意义?哪些无意义?为什么?
答:有意义的是
无意义的是
(
)
2
;
3
;
3
;
3
;
5
-
-
-
试一试
2.你知道下列式子表示什么意思吗 你能求出它们
的值吗
25
=5
4
1
=
2
1
0.81
=0.9
0
=0
例1 求下列各数的算术平方根:
(1)100 (2) (3)0.0001
解:(1)因为 =100,所以100的算术平方根为10,
即 =10。
(2)因为 = ,所以 的算术平方根是
,即 =
(3)因为 =0.0001,所以0.0001的算术平方
根为0.01,即 =0.01。
解(1)
注意:带分数化为假分数
注意:不要等于-25
1.判断:
(1)5是25的算术平方根;
(2)-6是 36 的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)-5是-25的算术平方根。
三、练习:
2:填空:
9
3
81
81
13
折纸游戏
如下图,是一个面积为4的正方形纸片.
(1)你能否利用此折出面积为1的小正方形
(2)你能折出面积为2的小正方形吗
(3)折出面积为2的小正方形的边长为多少
有多大
2
2
2
1
2
<
2
( )
2
<
因为
所以
2
<
<
1
2
因为
2
( )
2
<
<
1.4
2
1.5
2
所以
2
<
<
1.5
1.4
… …
1.414
2
<
<
1.415
2
=
1.4142135623730950
…
逼近法
无限不循环小数
本节作业
(1)书本p41 1,2
把同学们刚才所用的正方形看成面积为1的小正方形,你能用两个这样的正方形剪拼成面积为2的正方形吗
课外活动:
(2)用“逼近法”大致确定 的大小.
3
课后作业
第 六 章 实 数
—算术平方根
学校要举行美术作品比赛,小欧很
高兴,他想裁出一块面积为25dm 的正
方形画布,画上自己的得意之作参比
赛,这块正方形画布的边长应取多少?
2
5 dm
身边小事
§6.1 平方根
因为 =25
5
2
正方形的面积 1 9 16 36 0.25
边长
1
3
4
6
0.5
已知一个正数的平方,
算术平方根
求这个正数的问题.
如果一个正数 的平方等于 ,
x
a
x
一个正数
概念引入
那么5叫做25的算术平方根;
那么10叫做100的算术平方根;
a
x
即 = ,
2
那么这个正数 叫做 的
x
a
算术平方根.
一般地,
x
a
2
x
=
a
a
算术平方根
★ 说出下列各数的算术平方根:
9
4
3
的算术平方根是 3;
的算术平方根是 2,
的算术平方根记为
a
a,
读作:“ 根号 ”,
a
a
叫做被开方数,
x
=
a
,
9
=
4
=
规定:0的算术平方根是0,
即
0
=0.
10 =100,
2
象5 =25,
2
3
的算术平方根是
算术平方根的概念及性质
如果一个正数 的平方等于 ,
x
a
a
x
一个正数
a
x
即 = ,
2
那么这个正数 叫做 的
x
a
算术平方根.
一般地,
x
2
x
=
a
a
算术平方根
的算术平方根记为
a
a,
读作:“ 根号 ”,
a
a
叫做被开方数,
x
=
a
,
规定:0的算术平方根事0,
即
0
=0.
试一试
1.求下列各数的算术平方根:
解: (1)
因为 =100,
10
2
(5) 3
2
所以100的算术平方根为10,
即 =10.
100
(1) 100; (2) 1; (3) 0 ; (4) ;
64
49
(6) -4
(6)
因为没有一个数的平方可能是负数,
所以-4没有算术平方根.
≥
0
算术平方根的非负双重性.
对于 :
a
0
≥
a
a
}
例、下列各式中哪些有意义?哪些无意义?为什么?
答:有意义的是
无意义的是
(
)
2
;
3
;
3
;
3
;
5
-
-
-
试一试
2.你知道下列式子表示什么意思吗 你能求出它们
的值吗
25
=5
4
1
=
2
1
0.81
=0.9
0
=0
例1 求下列各数的算术平方根:
(1)100 (2) (3)0.0001
解:(1)因为 =100,所以100的算术平方根为10,
即 =10。
(2)因为 = ,所以 的算术平方根是
,即 =
(3)因为 =0.0001,所以0.0001的算术平方
根为0.01,即 =0.01。
解(1)
注意:带分数化为假分数
注意:不要等于-25
1.判断:
(1)5是25的算术平方根;
(2)-6是 36 的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)-5是-25的算术平方根。
三、练习:
2:填空:
9
3
81
81
13
折纸游戏
如下图,是一个面积为4的正方形纸片.
(1)你能否利用此折出面积为1的小正方形
(2)你能折出面积为2的小正方形吗
(3)折出面积为2的小正方形的边长为多少
有多大
2
2
2
1
2
<
2
( )
2
<
因为
所以
2
<
<
1
2
因为
2
( )
2
<
<
1.4
2
1.5
2
所以
2
<
<
1.5
1.4
… …
1.414
2
<
<
1.415
2
=
1.4142135623730950
…
逼近法
无限不循环小数
本节作业
(1)书本p41 1,2
把同学们刚才所用的正方形看成面积为1的小正方形,你能用两个这样的正方形剪拼成面积为2的正方形吗
课外活动:
(2)用“逼近法”大致确定 的大小.
3
课后作业
