人教版数学七年级下册 6.1.1平方根 (共25张PPT)
文档属性
| 名称 | 人教版数学七年级下册 6.1.1平方根 (共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 901.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 12:43:01 | ||
图片预览








文档简介
第六章 实数
6.1.1 平方根
————算术平方根
●卫星速度要大于第一宇宙
速度v, v的大小满足 v2=gR,
其中 g≈9.8 m/s2,
地球半径 R≈6.4×106 m,
怎么求v呢?
一、激发求知欲
二、展示目标和任务
学习目标:
(1)了解算术平方根的概念.
(2)会求一些数的算术平方根,并用算术平方根符号表示.
学习重点:
算术平方根的概念和求法.
请你说一说解决问题的思路.
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
三、自主合作与交流
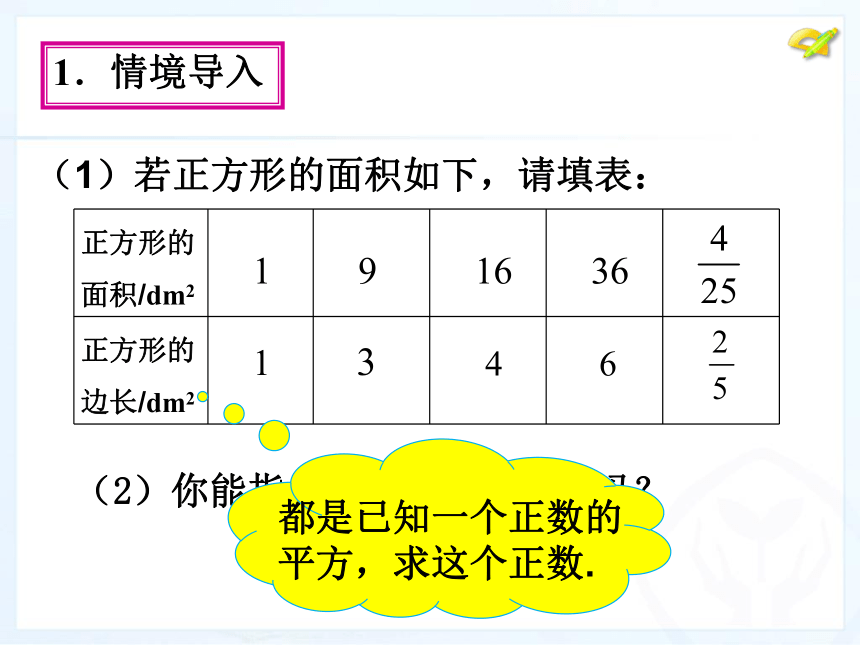
(1)若正方形的面积如下,请填表:
(2)你能指出它们的共同特点吗?
正方形的面积/dm2
1
9
16
36
正方形的边长/dm2
1.情境导入
都是已知一个正数的平方,求这个正数.
例如,由于 ,所以5是25的算术平方根,即 .
规定:0的算术平方根是0 ,也就是说,若 ,则 .
一般地,如果一个正数的平方等于 , 即 ,那么这个正数 叫做 的算术
平方根. 的算术平方根记为 ,读作
“根号 ”, 叫做被开方数.
2.总结概念
例1 求下列各数的算术平方根:
(1) ;(2) ;(3) .
解:(1)因为 ,
所以100的算术平方根是10 .
即 .
3.例题解析
解:(2)因为 ,
所以 的算术平方根是 .
即 .
3.例题解析
例1 求下列各数的算术平方根:
(1) ;(2) ;(3) .
解:(3)因为 ,
所以0.0001的算术平方根是0.01 .
即 .
3.例题解析
例1 求下列各数的算术平方根:
(1) ;(2) ;(3) .
(1)被开方数a的取值范围是什么?
(2)算术平方根x的取值范围是什么?
算术平方根定义:
若x2=a,则 .
a
≥
0
算术平方根的非负双重性.
0
≥
}
只有非负数才有算术平方根,算术平方根是非负的.
3.被开方数的取值范围
1、下列各式是否有意义,为什么?
2、下列各式中,x为何值时有意义?
∵-x≥0
∴x≤0
∵x2+1≥0恒成立
∴x为任何数
×
√
√
√
四、成果展示,教师点拨
1、什么叫算术平方根及表示方法
2、算术平方根成立的条件
3、会求一个正数的算术平方根
1、 a的算术平方根(a≥0)表示为_______.
2、 = 9, 则9的____________是3,
表示为 ______.
3、0的算术平方根是_____,表示为________.
算术平方根
0
0
=
0
a
32
3
五、知识验证提升
4.判断下列说法是否正确,若不正确请改正.
(1)5是25的算术平方根;
(2)-6是 36 的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)-3是-9的算术平方根.
5.算术平方根等于本身的数有___.
×
√
√
×
×
6
0.1
0.01
3
9
0和1
6.求下列各式的值:
(1) ;(2) ;(3) ;(4) .
解:(1) ;
(2) ;
(3) ;
(4) .
7.若 ,则x=___.
8.要使代数式 有意义,则 x的取值范围是( )
A. B. C. D.
9.求下列各数的算术平方根.
① 25 ② ③ 0.36 ④ 0 ⑤
B
9
5
0.6
0
2
=4
综合应用:
10.已知a、b满足等式 + =0,
求ab的值.
(1)什么是算术平方根?
如何求一个正数的算术平方根?
(2) 什么数才有算术平方根?
课堂小结
作业(必做题):
1.求下列各数的算术平方根.
121, , , .
2.求下列各式的值.
, , .
3.3x-4为25的算术平方根,求x的值.
4.已知9的算术平方根为a,b的绝对值为4,求a-b的值.
布置作业
作业(选做题):
5.已知2a-1的算术平方根是3,3a+b-1的算术平方根是4,求a、b的值.
6.若 与 互为相反数,求xy的算术平方根.
7.一个自然数的算术平方根为a (a>0),则与这个自然数相邻的两个自然数的算术平方根为____.
探究
能否用两个面积为1 dm2的小正方形
拼成一个面积为2 dm2的大正方形?
提出问题
能否用两个面积为1 dm2的小正方形
拼成一个面积为2 dm2的大正方形?
拼成的这个面积为 2 dm2 的大正方形的
边长应该是多少呢?
提出问题
?
解: 设大正方形的边长为x dm,
则
由算术平方根的定义,
得 .
所以大正方形的边长为 dm.
有多大呢?
这个无限不循环小数,它在哪两个整数之间呢?
解: ∵1<2<4
是一个无限不循环小数。
无限不循环小数是指小数位数无限,且小数部分为不循环的小数。
试一试:请你来估计 分别在哪两个整数之间?
讨论
1、估计大小:
(1)3与
(2)12与
(3) 与0.5
<
>
>
练习:课本44页2题
6.1.1 平方根
————算术平方根
●卫星速度要大于第一宇宙
速度v, v的大小满足 v2=gR,
其中 g≈9.8 m/s2,
地球半径 R≈6.4×106 m,
怎么求v呢?
一、激发求知欲
二、展示目标和任务
学习目标:
(1)了解算术平方根的概念.
(2)会求一些数的算术平方根,并用算术平方根符号表示.
学习重点:
算术平方根的概念和求法.
请你说一说解决问题的思路.
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
三、自主合作与交流
(1)若正方形的面积如下,请填表:
(2)你能指出它们的共同特点吗?
正方形的面积/dm2
1
9
16
36
正方形的边长/dm2
1.情境导入
都是已知一个正数的平方,求这个正数.
例如,由于 ,所以5是25的算术平方根,即 .
规定:0的算术平方根是0 ,也就是说,若 ,则 .
一般地,如果一个正数的平方等于 , 即 ,那么这个正数 叫做 的算术
平方根. 的算术平方根记为 ,读作
“根号 ”, 叫做被开方数.
2.总结概念
例1 求下列各数的算术平方根:
(1) ;(2) ;(3) .
解:(1)因为 ,
所以100的算术平方根是10 .
即 .
3.例题解析
解:(2)因为 ,
所以 的算术平方根是 .
即 .
3.例题解析
例1 求下列各数的算术平方根:
(1) ;(2) ;(3) .
解:(3)因为 ,
所以0.0001的算术平方根是0.01 .
即 .
3.例题解析
例1 求下列各数的算术平方根:
(1) ;(2) ;(3) .
(1)被开方数a的取值范围是什么?
(2)算术平方根x的取值范围是什么?
算术平方根定义:
若x2=a,则 .
a
≥
0
算术平方根的非负双重性.
0
≥
}
只有非负数才有算术平方根,算术平方根是非负的.
3.被开方数的取值范围
1、下列各式是否有意义,为什么?
2、下列各式中,x为何值时有意义?
∵-x≥0
∴x≤0
∵x2+1≥0恒成立
∴x为任何数
×
√
√
√
四、成果展示,教师点拨
1、什么叫算术平方根及表示方法
2、算术平方根成立的条件
3、会求一个正数的算术平方根
1、 a的算术平方根(a≥0)表示为_______.
2、 = 9, 则9的____________是3,
表示为 ______.
3、0的算术平方根是_____,表示为________.
算术平方根
0
0
=
0
a
32
3
五、知识验证提升
4.判断下列说法是否正确,若不正确请改正.
(1)5是25的算术平方根;
(2)-6是 36 的算术平方根;
(3)0的算术平方根是0;
(4)0.01是0.1的算术平方根;
(5)-3是-9的算术平方根.
5.算术平方根等于本身的数有___.
×
√
√
×
×
6
0.1
0.01
3
9
0和1
6.求下列各式的值:
(1) ;(2) ;(3) ;(4) .
解:(1) ;
(2) ;
(3) ;
(4) .
7.若 ,则x=___.
8.要使代数式 有意义,则 x的取值范围是( )
A. B. C. D.
9.求下列各数的算术平方根.
① 25 ② ③ 0.36 ④ 0 ⑤
B
9
5
0.6
0
2
=4
综合应用:
10.已知a、b满足等式 + =0,
求ab的值.
(1)什么是算术平方根?
如何求一个正数的算术平方根?
(2) 什么数才有算术平方根?
课堂小结
作业(必做题):
1.求下列各数的算术平方根.
121, , , .
2.求下列各式的值.
, , .
3.3x-4为25的算术平方根,求x的值.
4.已知9的算术平方根为a,b的绝对值为4,求a-b的值.
布置作业
作业(选做题):
5.已知2a-1的算术平方根是3,3a+b-1的算术平方根是4,求a、b的值.
6.若 与 互为相反数,求xy的算术平方根.
7.一个自然数的算术平方根为a (a>0),则与这个自然数相邻的两个自然数的算术平方根为____.
探究
能否用两个面积为1 dm2的小正方形
拼成一个面积为2 dm2的大正方形?
提出问题
能否用两个面积为1 dm2的小正方形
拼成一个面积为2 dm2的大正方形?
拼成的这个面积为 2 dm2 的大正方形的
边长应该是多少呢?
提出问题
?
解: 设大正方形的边长为x dm,
则
由算术平方根的定义,
得 .
所以大正方形的边长为 dm.
有多大呢?
这个无限不循环小数,它在哪两个整数之间呢?
解: ∵1<2<4
是一个无限不循环小数。
无限不循环小数是指小数位数无限,且小数部分为不循环的小数。
试一试:请你来估计 分别在哪两个整数之间?
讨论
1、估计大小:
(1)3与
(2)12与
(3) 与0.5
<
>
>
练习:课本44页2题
