人教版数学七年级下册 6.3.1《实数》课件(共23张PPT)
文档属性
| 名称 | 人教版数学七年级下册 6.3.1《实数》课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 18:06:39 | ||
图片预览








文档简介
3.0
2.5
-0.6
6.75
1.2
0.81
有限
无限循环
事实上,任何一个有理数都可以写成有限小数或无限循环小数的形式.反过来,任何有限小数或无限循环小数也都是_______数.
有理
叫做无理数.
所有的数都可以写成有限小数和无限循环小数的形式吗?如:
π=3.1415926535897932384626…
1.01001000100001…
(两个1之间依次多一个0)
无限不循环小数
探究新知
怎样识别无理数?
3.不循环的无限小数.
探究新知
注意:
2.无限小数不一定是无理数,无限不循环小数一定是无理数,如:1.1211211211112……
正无理数:
负无理数:
例 把下列各数分别填入相应的集合内:
有理数集合
无理数集合
6.3 实 数
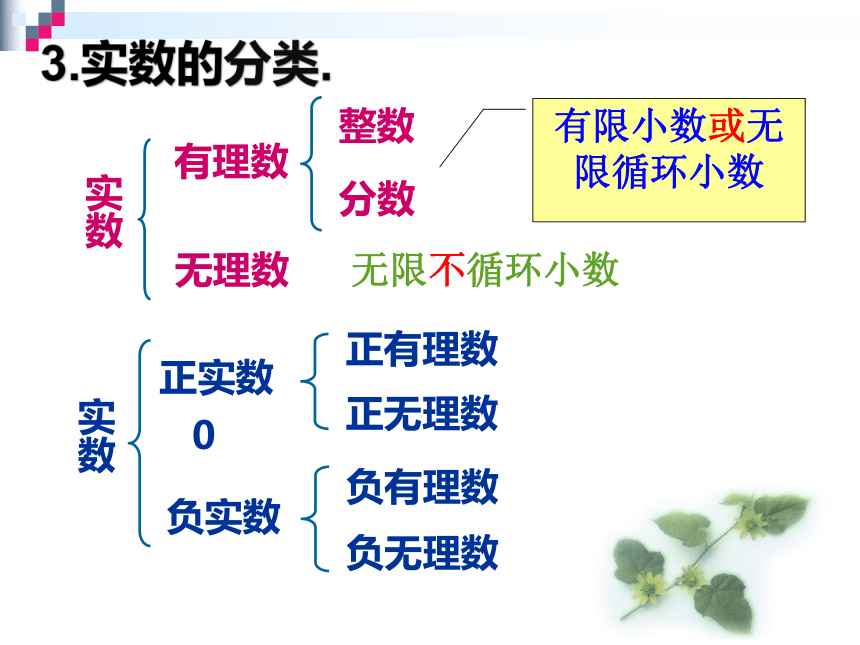
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
一.判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.无理数一定都带根号。 ( )
6.两个无理数之积不一定是无理数。 ( )
7.两个无理数之和一定是无理数。 ( )
×
×
×
8.有理数与无理数之和一定是无理数。( )
你能在数轴上找到表示 这样的无理数的点吗?
0
1
2
4
3
-1
-2
π
直径为1个单位长度的圆
探究
边长为1的正方形,对角线长为多少?
问题:
0
1
2
4
3
-1
-2
边长为1的正方形,对角线长为多少?
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
问题:
2.有理数和无理数统称实数.
6.3 实 数
4.实数与数轴上的点是一一对应的.
你能解答下列问题吗?
(1) 的相反数是 ,
的相反数是 ,
0 的相反数是 ;
(2) = , = ,
= .
探究新知
探究新知
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
a是一个实数,它的相反数为 ,如果
a 0,那么它的倒数为 .
2.有理数和无理数统称实数.
6.3 实 数
4.实数与数轴上的点是一一对应的.
5.实数 的相反数为 .
例1:
(1) 的相反数是 ;
的相反数是 .
(2) 的相反数是 ;
的相反数是 .
(3) 的绝对值是 .
(4) 绝对值是 的数是 .
3 .运用新知
2.有理数和无理数统称实数.
6.3 实 数
5.实数 的相反数为 .
2.有理数和无理数统称实数.
6.3 实 数
5.实数 的相反数为 .
6.实数的运算顺序
(1)先算乘方和开方;
(2)再算乘除,最后算加减;
(3)如果遇到括号,则先进行括号里的运算。
3.运用新知
例2 计算下列各式的值:
(1)
(2)
3.运用新知
例3 计算(结果保留小数点后两位):
;
解:
4.布置作业
1. 第57页 习题6.3 1-3、7、9题,
2.《新课堂》第28页,
3.预习第55-56页。
2.5
-0.6
6.75
1.2
0.81
有限
无限循环
事实上,任何一个有理数都可以写成有限小数或无限循环小数的形式.反过来,任何有限小数或无限循环小数也都是_______数.
有理
叫做无理数.
所有的数都可以写成有限小数和无限循环小数的形式吗?如:
π=3.1415926535897932384626…
1.01001000100001…
(两个1之间依次多一个0)
无限不循环小数
探究新知
怎样识别无理数?
3.不循环的无限小数.
探究新知
注意:
2.无限小数不一定是无理数,无限不循环小数一定是无理数,如:1.1211211211112……
正无理数:
负无理数:
例 把下列各数分别填入相应的集合内:
有理数集合
无理数集合
6.3 实 数
实数
实数
有理数
无理数
整数
分数
无限不循环小数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
有限小数或无限循环小数
一.判断:
1.实数不是有理数就是无理数。( )
2.无理数都是无限不循环小数。( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.无理数一定都带根号。 ( )
6.两个无理数之积不一定是无理数。 ( )
7.两个无理数之和一定是无理数。 ( )
×
×
×
8.有理数与无理数之和一定是无理数。( )
你能在数轴上找到表示 这样的无理数的点吗?
0
1
2
4
3
-1
-2
π
直径为1个单位长度的圆
探究
边长为1的正方形,对角线长为多少?
问题:
0
1
2
4
3
-1
-2
边长为1的正方形,对角线长为多少?
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
问题:
2.有理数和无理数统称实数.
6.3 实 数
4.实数与数轴上的点是一一对应的.
你能解答下列问题吗?
(1) 的相反数是 ,
的相反数是 ,
0 的相反数是 ;
(2) = , = ,
= .
探究新知
探究新知
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
a是一个实数,它的相反数为 ,如果
a 0,那么它的倒数为 .
2.有理数和无理数统称实数.
6.3 实 数
4.实数与数轴上的点是一一对应的.
5.实数 的相反数为 .
例1:
(1) 的相反数是 ;
的相反数是 .
(2) 的相反数是 ;
的相反数是 .
(3) 的绝对值是 .
(4) 绝对值是 的数是 .
3 .运用新知
2.有理数和无理数统称实数.
6.3 实 数
5.实数 的相反数为 .
2.有理数和无理数统称实数.
6.3 实 数
5.实数 的相反数为 .
6.实数的运算顺序
(1)先算乘方和开方;
(2)再算乘除,最后算加减;
(3)如果遇到括号,则先进行括号里的运算。
3.运用新知
例2 计算下列各式的值:
(1)
(2)
3.运用新知
例3 计算(结果保留小数点后两位):
;
解:
4.布置作业
1. 第57页 习题6.3 1-3、7、9题,
2.《新课堂》第28页,
3.预习第55-56页。
