人教版数学七年级下册7.1.2平面直角坐标系课件(共29张PPT)
文档属性
| 名称 | 人教版数学七年级下册7.1.2平面直角坐标系课件(共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 801.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 00:00:00 | ||
图片预览






文档简介
7.1.3平面直角坐标系
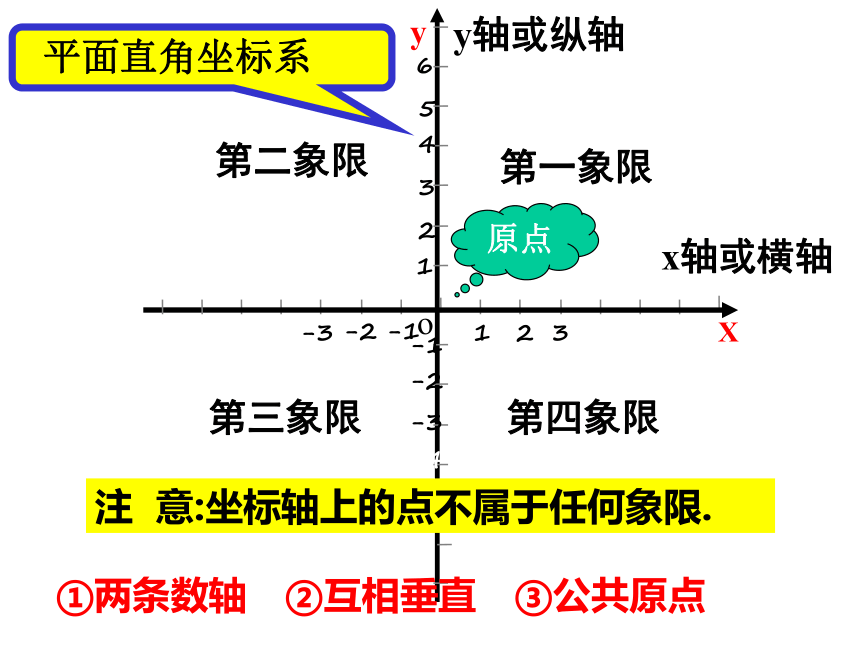
平面内两条互相垂直、原点重合的数轴,组成平面直角坐标系,水平方向的数轴称为x轴或横轴,习惯取向右的方向为正方向,竖直方向上的数轴称为y轴或纵轴,习惯取向上的方向为正方向;两坐标轴的交点是平面直角坐标系的原点 .
1.平面直角坐标系的概念:
一、激发求知欲
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
x轴或横轴
y轴或纵轴
原点
①两条数轴 ②互相垂直 ③公共原点
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
注 意:坐标轴上的点不属于任何象限.
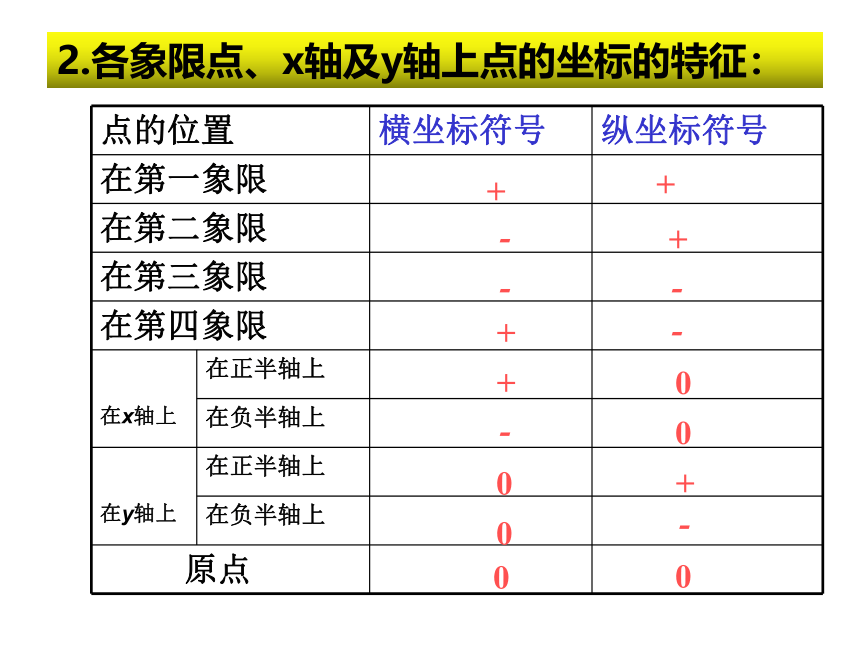
2.各象限点、x轴及y轴上点的坐标的特征:
点的位置
横坐标符号
纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在正半轴上
在x轴上
在负半轴上
在正半轴上
在y轴上
在负半轴上
原点
-
-
-
-
+
+
+
0
0
-
-
0
0
+
0
0
+
+
点P(a,b)到 x 轴的距离是_____
到 y 轴的距离是_____
︱b︱;
︱a︱;
3.点到坐标轴的距离:
例如:点(3,2)到x轴距离是 , 到y轴距离是
.
点(-6,-1.2)呢?
2
3
二、展示目标和任务
学习目标:
1.知道平面直角坐标系内特殊位置的点的符号特征.?
2.对于一个图形,能建立合适的坐标系表示图形上各点的坐标.?
3.知道坐标平面内的点与有序实数对是一一对应的,进一步体会数形结合思想,感受几何与代数间的联系.?
学习重难点:
各象限点的坐标的符号特点,建立合适的坐标系表示图形上各点的坐标.
三、自主合作与交流
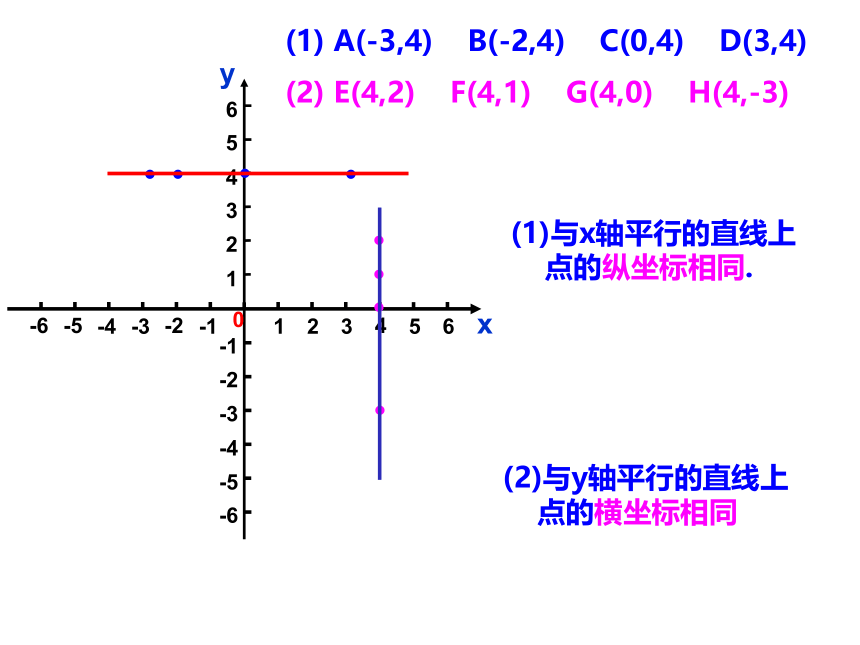
(1) A(-3,4) B(-2,4) C(0,4) D(3,4)
(2) E(4,2) F(4,1) G(4,0) H(4,-3)
1.请在平面直角坐标系中找出以下各点:
2.这些点有什么特点?
位置有什么关系?
第二组坐标的纵坐标相同
第一组坐标的横坐标相同
-1
-2
-4
-6
-5
-3
2
6
4
3
5
1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
y
x
0
(1) A(-3,4) B(-2,4) C(0,4) D(3,4)
(2) E(4,2) F(4,1) G(4,0) H(4,-3)
·
·
·
·
·
·
·
·
(1)与x轴平行的直线上
点的纵坐标相同.
(2)与y轴平行的直线上
点的横坐标相同
归纳1:
与坐标轴平行的直线上的点的坐标特征:
(1)与x轴平行的直线上点的纵坐标相同.
(2)与y轴平行的直线上点的横坐标相同
你能再找出一些具有上述特点的点吗?
练习
1.已知点A(m,-2),点B(3,m-1),
(1)若直线AB∥x轴,则m=_____
(2)若直线AB∥y轴,则m=_______
2.已知AB∥x轴,A点的坐标为
(3,2),并且AB=5,则B 的坐标为 .
- 1
3
(8,2)
或(-2,2)
1.请在平面直角坐标系中找出以下各点:
(1)A(3,3) B(2,2) C(-1,-1) D(-3,-3)
(2) E(-3,3) F(-2,2) G(3,-3) H(4,-4)
2.这些点有什么特点?位置有什么关系?
3.这些点到坐标轴的距离如何?
第一组坐标中的横坐标与纵坐标相等.
第二组坐标中的横坐标与纵坐标互为相反数.
-1
-2
-4
-6
-5
-3
2
6
4
3
5
1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
y
x
0
(1)A(3,3) B(2,2) C(-1,-1) D(-3,-3)
(2)E(-3,3) F(-2,2) G(3,-3) H(4,-4)
·C
·A
·B
E·
·D
G·
F·
H·
(2)第二,四象限角平分线上的点的横坐标与纵坐标互为相反数.
(1)第一,三象限角平分线上的点的横坐标与纵坐标相等.
归纳2:
坐标轴夹角平分线上点的坐标特征:
(1)第一,三象限角平分线上的点的横坐标与纵坐标相等.
(2)第二,四象限角平分线上的点的横坐标与纵坐标互为相反数.
1.已知点A(3a+5,4a-3)在第一三象限角平分线上,则a=___.
2.已知点A(3-m,2m-5)在第二四象限角平分线上,则m=___.
3.已知点A(-3+a,2b+9)在第二象限的
角平分线上,且a、 b互为相反数,则
a、b的值分别是____________.
6,-6
8
2
练习
1.在平面直角坐标系中描出下列各对点:
(1) A ( 2, 3 )与 B ( 2, -3 ) ,
C( -3, 4 )与D ( -3, -4 )
(2) E ( -2, 5 )与F ( 2, 5 ),
G( -4, -1 )与H ( 4, -1 )
(3) H ( 3, 2 )与I ( -3, -2 ),
J ( -4, 3 )与K ( 4, -3 )
2.观察上面各对点有什么关系?
3.它们到坐标轴或原点的距离如何?
-1
-2
-4
-6
-5
-3
2
6
4
3
5
1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
y
x
0
(1) A(2,3)与B(2,-3) C(-3,4)与D(-3,-4)
(2) E(-2,5)与F(2,5) G(-4,-1)与H(4,-1)
(3) M(3,2)与N(-3,-2) O(-4,3)与P(4,-3)
归纳:
(1)关于x轴对称的两点的
横坐标相同,纵坐标互
为相反数.
·C
·B
·A
·D
观察上面各对点有什么关系?
它们到坐标轴或原点的距离如何?
你能再找出一些类似的点吗?
-1
-2
-4
-6
-5
-3
2
6
4
3
5
1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
y
x
0
(1) A(2,3)与B(2,-3) C(-3,4)与D(-3,-4)
(2) E(-2,5)与F(2,5) G(-4,-1)与H(4,-1)
(3) M(3,2)与N(-3,-2) O(-4,3)与P(4,-3)
归纳:
(1)关于x轴对称的两点的
横坐标相同,纵坐标互
为相反数.
·E
·G
·F
·H
(2)关于y轴对称的两点的
纵坐标相同,横坐标互
为相反数
观察上面各对点有什么关系?
它们到坐标轴或原点的距离如何?
你能再找出一些类似的点吗?
-1
-2
-4
-6
-5
-3
2
6
4
3
5
1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
y
x
0
(1) A(2,3)与B(2,-3) C(-3,4)与D(-3,-4)
(2) E(-2,5)与F(2,5) G(-4,-1)与H(4,-1)
(3) M(3,2)与N(-3,-2) O(-4,3)与P(4,-3)
归纳:
(1)关于x轴对称的两点的
横坐标相同,纵坐标互
为相反数.
·O
·P
·N
·M
(2)关于y轴对称的两点的
纵坐标相同,横坐标互
为相反数
(3)关于原点对称的两点的
横,纵坐标分别互为相
反数
观察上面各对点有什么关系?
它们到坐标轴或原点的距离如何?
你能再找出一些类似的点吗?
(1)关于x轴对称的两点的横坐标相同,纵坐标互为相反数.
(3)关于原点对称的两点的横,纵坐标分别互为相反数
归纳3:关于x轴、y轴、原点对称
的两点的坐标特征:
(2)关于y轴对称的两点的纵坐标相同,
横坐标互为相反数
练习
1、点(-2,4)关于X轴对称的点是 .
关于y轴对称的点是 .
关于原点对称的点是 .
2、点A(-3,b)与点B(a,-2)关于X轴对称,
则a= , b= .
3、点C(a+b,b)与D(-4,5)关于y轴对称,
则a= , b= .
点C关于原点对称的点是 .
(-2,-4)
(2,4)
(2,-4)
-3
2
5
-1
(-4,-5)
四、成果展示,教师点拨
1、与坐标轴平行的直线上的点的坐标特征:
(1)与x轴平行的直线上点的纵坐标相同.
(2)与y轴平行的直线上点的横坐标相同
2、坐标轴夹角平分线上点的坐标特征:
(1)第一,三象限角平分线上的点的横坐标与纵坐标相等.
(2)第二,四象限角平分线上的点的横坐标与纵坐标互为相反数.
3、关于x轴、 y轴、原点对称的两点的坐标特征:
(1)关于x轴对称的两点的横坐标相同,纵坐标互为相反数.
(2)关于y轴对称的两点的纵坐标相同,横坐标互为相反数
(3)关于原点对称的两点的横,纵坐标分别互为相反数
1、下列各点 A(-3,2) B(-4,5) C(4,5)
D(3,-1) E(-4,-3) F(2,-3)
点 与点 的连线平行于x轴.还有吗?
点 与点 的连线平行于y轴.还有吗?
B(-4,5)
C(4,5)
E(-4,-3)
F(2,-3)
B(-4,5)
E(-4,-3)
五、知识验证提升
练习:
2、已知点p(-5,a) Q(a+1,3)
<1>若PQ//X轴,则a= .
此时点P坐标为 .点Q坐标为 .
<2>若PQ//y轴,则a= .
此时点P坐标为 .点Q坐标为 .
3
-6
p(-5,3)
Q(4,3)
p(-5,-6)
Q(-5,3)
3、已知MN//x轴,点M(4a-8,a+8),N(3,6)
则点M的坐标为 .
4、若MN//y轴,点M(3-2b,b+1),N(5,-2)
则点M的坐标为 .
M(-16,6)
M(5,0)
练习
5、下列各点 A(-3,3) B(4,-4) C(-2, )
D(3,-5) E(-5,-5) F(2,2) G( ,2.5)
H(-2,4) I(6,7) J(0,0) K( ,-0.25)
在二,四象限角平分线上的点是:
.
E(-5,-5) F(2,2) J(0,0) K( ,-0.25)
A(-3,3) B(4,-4) G( ,2.5) J(0,0)
在一,三象限角平分线上的点是:
.
6、若点A(2a-2,4a)在一,三象限的角平分线
上,则a= ,点A的坐标为 .
7、若点B(4-b,2+2b)在二,四象限的角平分线
上,则b= ,点B的坐标为 .
8、若p(a+1,2a-1)在坐标轴夹角平分线上,则
a= ,点P的坐标为 .
-1
P(3,3)或P(1,-1)
2或0
B(10,-10)
A(-4,-4)
-6
练习
9、点(-2,4)关于X轴对称的点是 .
关于y轴对称的点是 .
关于原点对称的点是 .
10、点A(-3,b)与点B(a,-2)关于X轴对称,
则a= , b= .
11、点C(a+b,b)与D(-4,5)关于y轴对称,
则a= , b= .
点C关于原点对称的点是 .
(-2,-4)
(2,4)
(2,-4)
-3
2
5
-1
(-4,-5)
12、点E(2m+n,n-2)与F(-1,-3)关于原点对称
则m= , n= .
13、写出下列各点分别关于x轴,y轴,原点的对称点.
关于x轴 关于y轴 关于原点
(-4,-6)
(-7,3)
(3,2)
(1,-5)
(-1,5)
(-3,-2)
(-1,-5)
(-3,2)
(7,-3)
(7,3)
(4,-6)
(4,6)
A(-4,6)
B(-7,-3)
C(3,-2)
D(1,5)
1
2
3
4
5
-2
2、坐标轴夹角平分线上点的坐标特征:
(1)第一,三象限角平分线上的点的横坐标与纵坐标相等.
(2)第二,四象限角平分线上的点的横坐标与纵坐标互为相反数.
1、与坐标轴平行的直线上的点的坐标特征:
(1)与x轴平行的直线上点的纵坐标相同.
(2)与y轴平行的直线上点的横坐标相同
3、关于x轴、 y轴、原点对称的两点的坐标特征:
(1)关于x轴对称的两点的横坐标相同,纵坐标互为相反数.
(2)关于y轴对称的两点的纵坐标相同,横坐标互为相反数
(3)关于原点对称的两点的横,纵坐标分别互为相反数
平面内两条互相垂直、原点重合的数轴,组成平面直角坐标系,水平方向的数轴称为x轴或横轴,习惯取向右的方向为正方向,竖直方向上的数轴称为y轴或纵轴,习惯取向上的方向为正方向;两坐标轴的交点是平面直角坐标系的原点 .
1.平面直角坐标系的概念:
一、激发求知欲
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
x轴或横轴
y轴或纵轴
原点
①两条数轴 ②互相垂直 ③公共原点
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
注 意:坐标轴上的点不属于任何象限.
2.各象限点、x轴及y轴上点的坐标的特征:
点的位置
横坐标符号
纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在正半轴上
在x轴上
在负半轴上
在正半轴上
在y轴上
在负半轴上
原点
-
-
-
-
+
+
+
0
0
-
-
0
0
+
0
0
+
+
点P(a,b)到 x 轴的距离是_____
到 y 轴的距离是_____
︱b︱;
︱a︱;
3.点到坐标轴的距离:
例如:点(3,2)到x轴距离是 , 到y轴距离是
.
点(-6,-1.2)呢?
2
3
二、展示目标和任务
学习目标:
1.知道平面直角坐标系内特殊位置的点的符号特征.?
2.对于一个图形,能建立合适的坐标系表示图形上各点的坐标.?
3.知道坐标平面内的点与有序实数对是一一对应的,进一步体会数形结合思想,感受几何与代数间的联系.?
学习重难点:
各象限点的坐标的符号特点,建立合适的坐标系表示图形上各点的坐标.
三、自主合作与交流
(1) A(-3,4) B(-2,4) C(0,4) D(3,4)
(2) E(4,2) F(4,1) G(4,0) H(4,-3)
1.请在平面直角坐标系中找出以下各点:
2.这些点有什么特点?
位置有什么关系?
第二组坐标的纵坐标相同
第一组坐标的横坐标相同
-1
-2
-4
-6
-5
-3
2
6
4
3
5
1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
y
x
0
(1) A(-3,4) B(-2,4) C(0,4) D(3,4)
(2) E(4,2) F(4,1) G(4,0) H(4,-3)
·
·
·
·
·
·
·
·
(1)与x轴平行的直线上
点的纵坐标相同.
(2)与y轴平行的直线上
点的横坐标相同
归纳1:
与坐标轴平行的直线上的点的坐标特征:
(1)与x轴平行的直线上点的纵坐标相同.
(2)与y轴平行的直线上点的横坐标相同
你能再找出一些具有上述特点的点吗?
练习
1.已知点A(m,-2),点B(3,m-1),
(1)若直线AB∥x轴,则m=_____
(2)若直线AB∥y轴,则m=_______
2.已知AB∥x轴,A点的坐标为
(3,2),并且AB=5,则B 的坐标为 .
- 1
3
(8,2)
或(-2,2)
1.请在平面直角坐标系中找出以下各点:
(1)A(3,3) B(2,2) C(-1,-1) D(-3,-3)
(2) E(-3,3) F(-2,2) G(3,-3) H(4,-4)
2.这些点有什么特点?位置有什么关系?
3.这些点到坐标轴的距离如何?
第一组坐标中的横坐标与纵坐标相等.
第二组坐标中的横坐标与纵坐标互为相反数.
-1
-2
-4
-6
-5
-3
2
6
4
3
5
1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
y
x
0
(1)A(3,3) B(2,2) C(-1,-1) D(-3,-3)
(2)E(-3,3) F(-2,2) G(3,-3) H(4,-4)
·C
·A
·B
E·
·D
G·
F·
H·
(2)第二,四象限角平分线上的点的横坐标与纵坐标互为相反数.
(1)第一,三象限角平分线上的点的横坐标与纵坐标相等.
归纳2:
坐标轴夹角平分线上点的坐标特征:
(1)第一,三象限角平分线上的点的横坐标与纵坐标相等.
(2)第二,四象限角平分线上的点的横坐标与纵坐标互为相反数.
1.已知点A(3a+5,4a-3)在第一三象限角平分线上,则a=___.
2.已知点A(3-m,2m-5)在第二四象限角平分线上,则m=___.
3.已知点A(-3+a,2b+9)在第二象限的
角平分线上,且a、 b互为相反数,则
a、b的值分别是____________.
6,-6
8
2
练习
1.在平面直角坐标系中描出下列各对点:
(1) A ( 2, 3 )与 B ( 2, -3 ) ,
C( -3, 4 )与D ( -3, -4 )
(2) E ( -2, 5 )与F ( 2, 5 ),
G( -4, -1 )与H ( 4, -1 )
(3) H ( 3, 2 )与I ( -3, -2 ),
J ( -4, 3 )与K ( 4, -3 )
2.观察上面各对点有什么关系?
3.它们到坐标轴或原点的距离如何?
-1
-2
-4
-6
-5
-3
2
6
4
3
5
1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
y
x
0
(1) A(2,3)与B(2,-3) C(-3,4)与D(-3,-4)
(2) E(-2,5)与F(2,5) G(-4,-1)与H(4,-1)
(3) M(3,2)与N(-3,-2) O(-4,3)与P(4,-3)
归纳:
(1)关于x轴对称的两点的
横坐标相同,纵坐标互
为相反数.
·C
·B
·A
·D
观察上面各对点有什么关系?
它们到坐标轴或原点的距离如何?
你能再找出一些类似的点吗?
-1
-2
-4
-6
-5
-3
2
6
4
3
5
1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
y
x
0
(1) A(2,3)与B(2,-3) C(-3,4)与D(-3,-4)
(2) E(-2,5)与F(2,5) G(-4,-1)与H(4,-1)
(3) M(3,2)与N(-3,-2) O(-4,3)与P(4,-3)
归纳:
(1)关于x轴对称的两点的
横坐标相同,纵坐标互
为相反数.
·E
·G
·F
·H
(2)关于y轴对称的两点的
纵坐标相同,横坐标互
为相反数
观察上面各对点有什么关系?
它们到坐标轴或原点的距离如何?
你能再找出一些类似的点吗?
-1
-2
-4
-6
-5
-3
2
6
4
3
5
1
-1
-2
-3
-4
-5
-6
1
2
3
4
5
6
y
x
0
(1) A(2,3)与B(2,-3) C(-3,4)与D(-3,-4)
(2) E(-2,5)与F(2,5) G(-4,-1)与H(4,-1)
(3) M(3,2)与N(-3,-2) O(-4,3)与P(4,-3)
归纳:
(1)关于x轴对称的两点的
横坐标相同,纵坐标互
为相反数.
·O
·P
·N
·M
(2)关于y轴对称的两点的
纵坐标相同,横坐标互
为相反数
(3)关于原点对称的两点的
横,纵坐标分别互为相
反数
观察上面各对点有什么关系?
它们到坐标轴或原点的距离如何?
你能再找出一些类似的点吗?
(1)关于x轴对称的两点的横坐标相同,纵坐标互为相反数.
(3)关于原点对称的两点的横,纵坐标分别互为相反数
归纳3:关于x轴、y轴、原点对称
的两点的坐标特征:
(2)关于y轴对称的两点的纵坐标相同,
横坐标互为相反数
练习
1、点(-2,4)关于X轴对称的点是 .
关于y轴对称的点是 .
关于原点对称的点是 .
2、点A(-3,b)与点B(a,-2)关于X轴对称,
则a= , b= .
3、点C(a+b,b)与D(-4,5)关于y轴对称,
则a= , b= .
点C关于原点对称的点是 .
(-2,-4)
(2,4)
(2,-4)
-3
2
5
-1
(-4,-5)
四、成果展示,教师点拨
1、与坐标轴平行的直线上的点的坐标特征:
(1)与x轴平行的直线上点的纵坐标相同.
(2)与y轴平行的直线上点的横坐标相同
2、坐标轴夹角平分线上点的坐标特征:
(1)第一,三象限角平分线上的点的横坐标与纵坐标相等.
(2)第二,四象限角平分线上的点的横坐标与纵坐标互为相反数.
3、关于x轴、 y轴、原点对称的两点的坐标特征:
(1)关于x轴对称的两点的横坐标相同,纵坐标互为相反数.
(2)关于y轴对称的两点的纵坐标相同,横坐标互为相反数
(3)关于原点对称的两点的横,纵坐标分别互为相反数
1、下列各点 A(-3,2) B(-4,5) C(4,5)
D(3,-1) E(-4,-3) F(2,-3)
点 与点 的连线平行于x轴.还有吗?
点 与点 的连线平行于y轴.还有吗?
B(-4,5)
C(4,5)
E(-4,-3)
F(2,-3)
B(-4,5)
E(-4,-3)
五、知识验证提升
练习:
2、已知点p(-5,a) Q(a+1,3)
<1>若PQ//X轴,则a= .
此时点P坐标为 .点Q坐标为 .
<2>若PQ//y轴,则a= .
此时点P坐标为 .点Q坐标为 .
3
-6
p(-5,3)
Q(4,3)
p(-5,-6)
Q(-5,3)
3、已知MN//x轴,点M(4a-8,a+8),N(3,6)
则点M的坐标为 .
4、若MN//y轴,点M(3-2b,b+1),N(5,-2)
则点M的坐标为 .
M(-16,6)
M(5,0)
练习
5、下列各点 A(-3,3) B(4,-4) C(-2, )
D(3,-5) E(-5,-5) F(2,2) G( ,2.5)
H(-2,4) I(6,7) J(0,0) K( ,-0.25)
在二,四象限角平分线上的点是:
.
E(-5,-5) F(2,2) J(0,0) K( ,-0.25)
A(-3,3) B(4,-4) G( ,2.5) J(0,0)
在一,三象限角平分线上的点是:
.
6、若点A(2a-2,4a)在一,三象限的角平分线
上,则a= ,点A的坐标为 .
7、若点B(4-b,2+2b)在二,四象限的角平分线
上,则b= ,点B的坐标为 .
8、若p(a+1,2a-1)在坐标轴夹角平分线上,则
a= ,点P的坐标为 .
-1
P(3,3)或P(1,-1)
2或0
B(10,-10)
A(-4,-4)
-6
练习
9、点(-2,4)关于X轴对称的点是 .
关于y轴对称的点是 .
关于原点对称的点是 .
10、点A(-3,b)与点B(a,-2)关于X轴对称,
则a= , b= .
11、点C(a+b,b)与D(-4,5)关于y轴对称,
则a= , b= .
点C关于原点对称的点是 .
(-2,-4)
(2,4)
(2,-4)
-3
2
5
-1
(-4,-5)
12、点E(2m+n,n-2)与F(-1,-3)关于原点对称
则m= , n= .
13、写出下列各点分别关于x轴,y轴,原点的对称点.
关于x轴 关于y轴 关于原点
(-4,-6)
(-7,3)
(3,2)
(1,-5)
(-1,5)
(-3,-2)
(-1,-5)
(-3,2)
(7,-3)
(7,3)
(4,-6)
(4,6)
A(-4,6)
B(-7,-3)
C(3,-2)
D(1,5)
1
2
3
4
5
-2
2、坐标轴夹角平分线上点的坐标特征:
(1)第一,三象限角平分线上的点的横坐标与纵坐标相等.
(2)第二,四象限角平分线上的点的横坐标与纵坐标互为相反数.
1、与坐标轴平行的直线上的点的坐标特征:
(1)与x轴平行的直线上点的纵坐标相同.
(2)与y轴平行的直线上点的横坐标相同
3、关于x轴、 y轴、原点对称的两点的坐标特征:
(1)关于x轴对称的两点的横坐标相同,纵坐标互为相反数.
(2)关于y轴对称的两点的纵坐标相同,横坐标互为相反数
(3)关于原点对称的两点的横,纵坐标分别互为相反数
