人教版数学七年级下册8.2.2《用适当的方法解二元一次方程组》课件(共17张PPT)
文档属性
| 名称 | 人教版数学七年级下册8.2.2《用适当的方法解二元一次方程组》课件(共17张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 17.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 11:33:40 | ||
图片预览



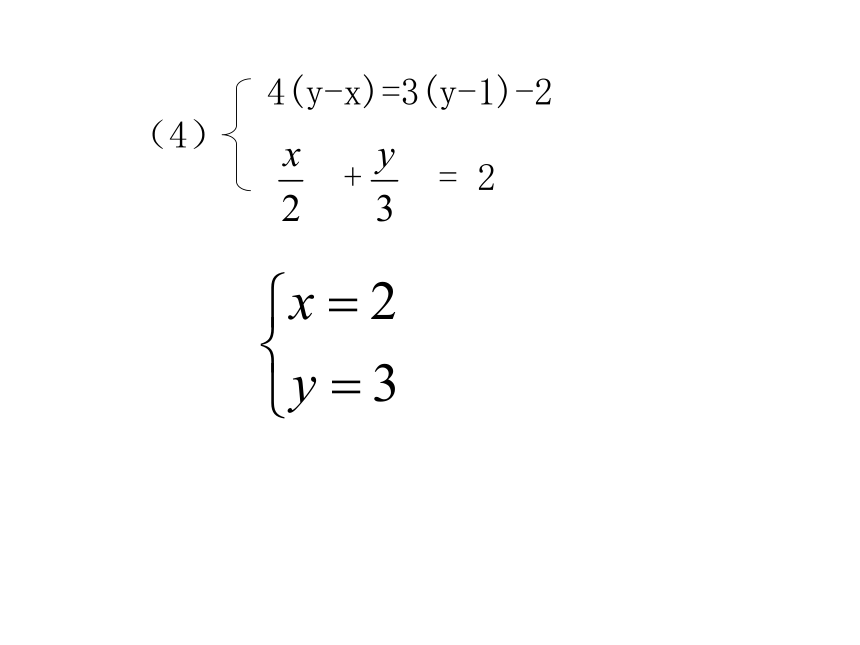

文档简介
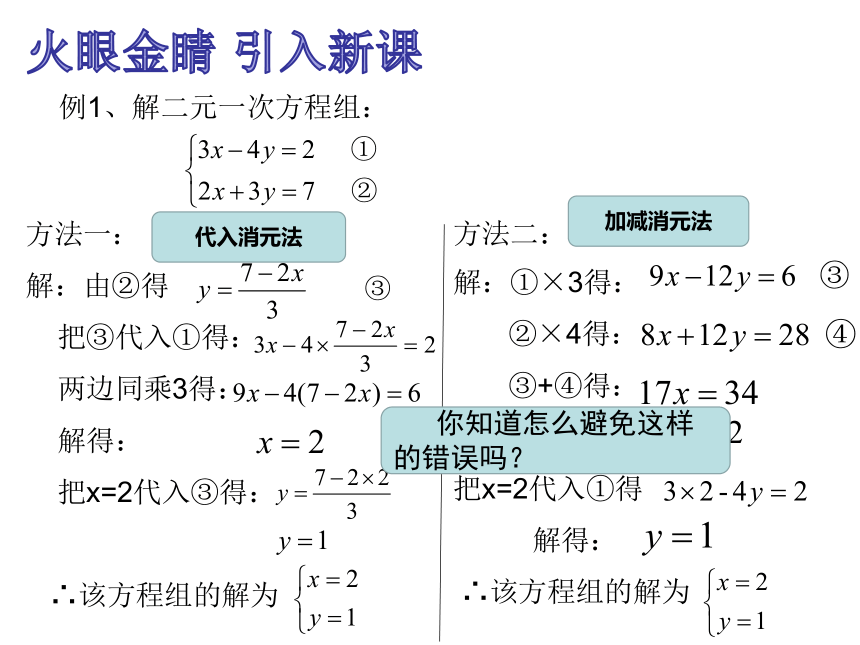
例1、解二元一次方程组:
解:由②得
把③代入①得:
两边同乘3得:
解得:
把x=2代入③得:
∴该方程组的解为
火眼金睛 引入新课
以下是小明的解题过程。请你帮他检验是否正确。
你能指出错误原因吗?
例1、解二元一次方程组:
方法一:
解:由②得
把③代入①得:
两边同乘3得:
解得:
把x=2代入③得:
∴该方程组的解为
方法二:
代入消元法
解:①×3得:
②×4得:
③+④得:
解得
把x=2代入①得
解得:
∴该方程组的解为
加减消元法
你知道怎么避免这样的错误吗?
火眼金睛 引入新课
8.2 消元——解二元一次方程组(4)
用适当的方法解二元一次方程组
1.请你选择适当的方法解下列方程组:
x=9-4y
3x-2y=-5
(1)
(2)
3u-2t=7
6u+2t=11
①
①
②
②
2x-5y=-1
4x+y=9
①
②
(3)
(4)
4(y-x)=3(y-1)-2
+ = 2
总结:
1、代入消元:
2、加减法:
方程组中有一个未知数的系数为1(或-1)。
(3)求同一系数的最小公倍数。
特别强调:对于较复杂的二元一次方程组应先化简(去分母、去括号、合并同类项等)
(1)方程组中有某个未知数的系数相同或互为相反数;
(2)同一个未知数的系数成倍数关系;
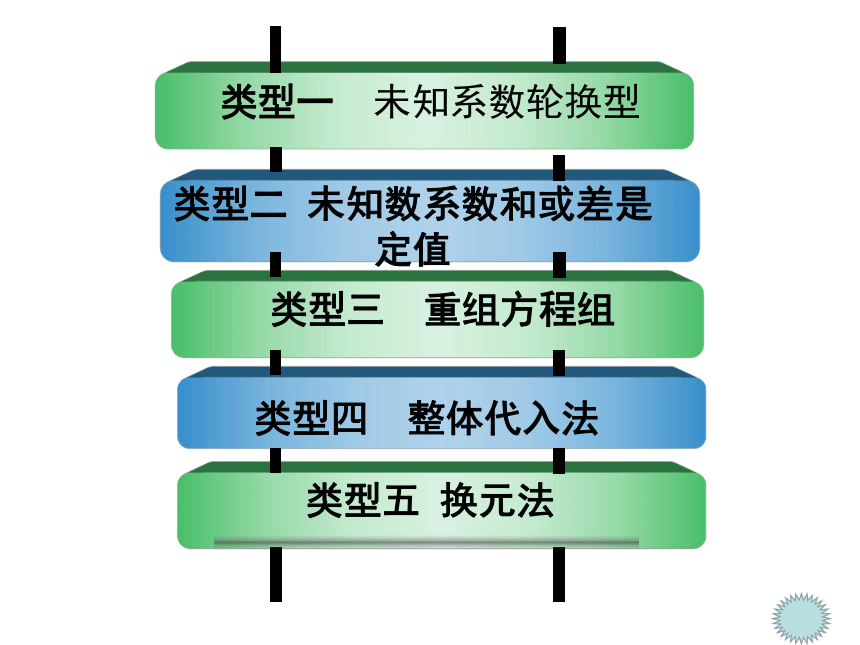
类型一 未知系数轮换型
类型五 换元法
类型四 整体代入法
类型二 未知数系数和或差是定值
类型三 重组方程组
1.用简便方法解方程组:
53x+47y=112
47x+53y=88
解:①+②得:100x+100y=200
即:x+y=2 ③
①-② 得:6x-6y=24
即:x-y=4 ④
把x=3代入③解得:y=-1
③+④得:2x=6
解得 x=3
所以这个方程组的解是
x=3
y=-1
①
②
合作互学
类型一 未知系数轮换型
一
2.如果二元一次方程组
那么x+y=_____ ,x-y=_____
5
-1
类型二 未知数系数和(差)是定值
二
解析:①+②得 3x+3y=15
两边都除以3得 x+y=5
解:①-②得
x-y=-1
3.若关于x,y得二元一次方程组 ,与
有相同得解,求a,b的值。
类型三 重组方程组求未知数的值
三
解析:因为两个方程组有相同的解,所以可以先解
求出x,y的值,再代入方程组
得到关于a,b的方程组,进而
求出a,b的值。
4.先阅读材料,后解方程组.
材料:解方程组
时,可由①得x-y=1 ③
将③代入②得4×1-y=5.
即y=-1.
进一步得
这种解方程组的方法称为
“整体代入法”.
请用整体代入法解方程组
类型四 整体代入法
四
5、解方程组
分析:本题含有相同的式子,可用换元法求解。
解:设 , ,
原方程化为
解得
原方程组变为
即 解得
换元思想是重要的数学思想,望掌握!
类型五 换元法
五
四、运用活学:
1、解下列方程组:
(1) (2)
3.若|a+b+1|与 互为相反数,则a与b的大小关系是( )
A.a>b B.a=b C.a<b D.a≥b
2、已知方程组 ,则x+y的值为( )
A.-1 B.0 C.2 D.3
(一)课内检测:
D
C
四、运用活学:
4、已知关于x,y的方程组 的解也是二元一次方程x+y=2解,求k的值。
5、已知方程 的解满足x+y=1,求m的值。
(一)课内检测:
提示:两方程相减得x+y=k-2,从而得到k-2=2得k=4.
提示:两方程相加得x=y=m,很明显得到m=1.
四、运用活学:
(二)课外补充:
1、已知方程组 中未知数的和等
于-1,求m的值。
1、选择适当的方法解二元一次方程组。
2、体会数学思想能使问题从难到易,不会到会的过程。
总结归纳
谢谢大家! 再见!
解:由②得
把③代入①得:
两边同乘3得:
解得:
把x=2代入③得:
∴该方程组的解为
火眼金睛 引入新课
以下是小明的解题过程。请你帮他检验是否正确。
你能指出错误原因吗?
例1、解二元一次方程组:
方法一:
解:由②得
把③代入①得:
两边同乘3得:
解得:
把x=2代入③得:
∴该方程组的解为
方法二:
代入消元法
解:①×3得:
②×4得:
③+④得:
解得
把x=2代入①得
解得:
∴该方程组的解为
加减消元法
你知道怎么避免这样的错误吗?
火眼金睛 引入新课
8.2 消元——解二元一次方程组(4)
用适当的方法解二元一次方程组
1.请你选择适当的方法解下列方程组:
x=9-4y
3x-2y=-5
(1)
(2)
3u-2t=7
6u+2t=11
①
①
②
②
2x-5y=-1
4x+y=9
①
②
(3)
(4)
4(y-x)=3(y-1)-2
+ = 2
总结:
1、代入消元:
2、加减法:
方程组中有一个未知数的系数为1(或-1)。
(3)求同一系数的最小公倍数。
特别强调:对于较复杂的二元一次方程组应先化简(去分母、去括号、合并同类项等)
(1)方程组中有某个未知数的系数相同或互为相反数;
(2)同一个未知数的系数成倍数关系;
类型一 未知系数轮换型
类型五 换元法
类型四 整体代入法
类型二 未知数系数和或差是定值
类型三 重组方程组
1.用简便方法解方程组:
53x+47y=112
47x+53y=88
解:①+②得:100x+100y=200
即:x+y=2 ③
①-② 得:6x-6y=24
即:x-y=4 ④
把x=3代入③解得:y=-1
③+④得:2x=6
解得 x=3
所以这个方程组的解是
x=3
y=-1
①
②
合作互学
类型一 未知系数轮换型
一
2.如果二元一次方程组
那么x+y=_____ ,x-y=_____
5
-1
类型二 未知数系数和(差)是定值
二
解析:①+②得 3x+3y=15
两边都除以3得 x+y=5
解:①-②得
x-y=-1
3.若关于x,y得二元一次方程组 ,与
有相同得解,求a,b的值。
类型三 重组方程组求未知数的值
三
解析:因为两个方程组有相同的解,所以可以先解
求出x,y的值,再代入方程组
得到关于a,b的方程组,进而
求出a,b的值。
4.先阅读材料,后解方程组.
材料:解方程组
时,可由①得x-y=1 ③
将③代入②得4×1-y=5.
即y=-1.
进一步得
这种解方程组的方法称为
“整体代入法”.
请用整体代入法解方程组
类型四 整体代入法
四
5、解方程组
分析:本题含有相同的式子,可用换元法求解。
解:设 , ,
原方程化为
解得
原方程组变为
即 解得
换元思想是重要的数学思想,望掌握!
类型五 换元法
五
四、运用活学:
1、解下列方程组:
(1) (2)
3.若|a+b+1|与 互为相反数,则a与b的大小关系是( )
A.a>b B.a=b C.a<b D.a≥b
2、已知方程组 ,则x+y的值为( )
A.-1 B.0 C.2 D.3
(一)课内检测:
D
C
四、运用活学:
4、已知关于x,y的方程组 的解也是二元一次方程x+y=2解,求k的值。
5、已知方程 的解满足x+y=1,求m的值。
(一)课内检测:
提示:两方程相减得x+y=k-2,从而得到k-2=2得k=4.
提示:两方程相加得x=y=m,很明显得到m=1.
四、运用活学:
(二)课外补充:
1、已知方程组 中未知数的和等
于-1,求m的值。
1、选择适当的方法解二元一次方程组。
2、体会数学思想能使问题从难到易,不会到会的过程。
总结归纳
谢谢大家! 再见!
