人教版数学七下9.1.2不等式的性质(1)(共34张PPT)
文档属性
| 名称 | 人教版数学七下9.1.2不等式的性质(1)(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-01 12:36:09 | ||
图片预览









文档简介
1.用不等式表示下列关系:
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的4倍小于或等于-2;
一、激发求知欲
2.等式的性质
猜想:不等式也具有同样的性质吗?
二、展示目标和任务
学习目标:
1、掌握不等式的三个基本性质。?
2、经历探究不等式基本性质的过程,体会不等式与等式的异同点。?
3、体会探索过程中所应用的归纳和类比方法。??
学习重点:
理解不等式的三个基本性质。??
学习难点:
对不等式的基本性质3的认识。
1.用 > 或 < 符号填空,并总结其中的规律:
(1) 5>3 , 5+2 3+2, 5-2 3-2
(2) -1<3, -1+2 3+2, -1-3 3-3
(3) 6>2, 6×5 2×5, 6×(-5) 2×(-5)
(4) -2<3, (-2)×6 3×6, (-2)×(-6) 3×(-6)
>
>
<
<
>
<
>
>
三、自主合作与交流
2.从以上练习中,你发现了什么规律?
(1)不等式的两边同时加(或减)同一个数,不等号的方向__________.
(2)不等式的两边同时乘(或除以)同一个正数,不等号的方向______________.
(3)不等式的两边同时乘(或除以)同一个负数,不等号的方向______________.
不变
不变
改变
教学目标
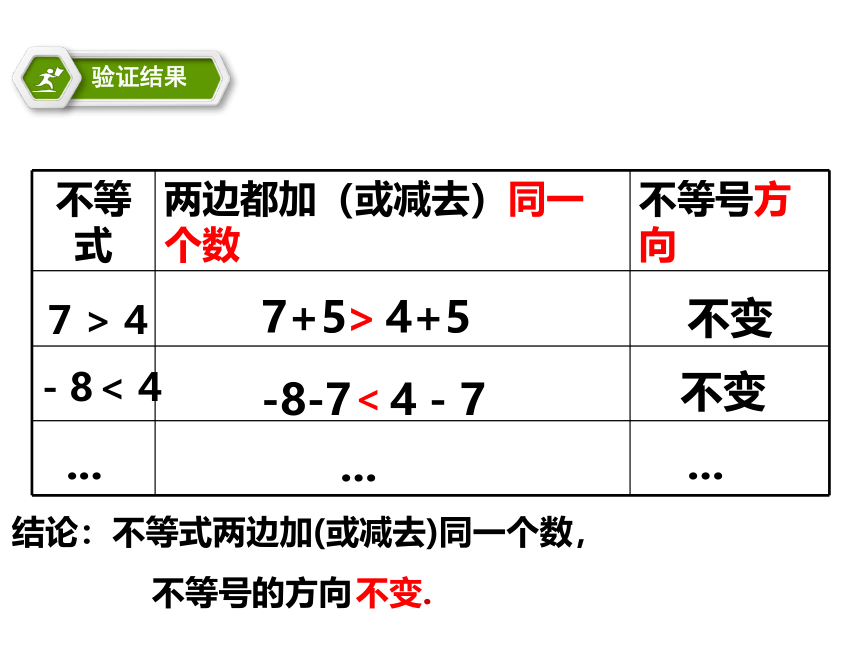
不等式
两边都加(或减去)同一个数
不等号方向
-8<4
7+5 4+5
-8-7 4-7
不变
不变
7>4
...
...
...
结论:不等式两边加(或减去)同一个数,
不等号的方向 不变.
>
<
教学目标
7×5 4×5
-8÷2 4÷2
结论:不等式两边乘或除以同一个正数,
不等号的方向不变.
>
<
教学目标
不等式
两边都加(或减去)同一个数
不等号方向
-8<4
不变
不变
7>4
...
...
...
不等式
两边都乘(或除以)同一正数
不等号方向
-8<4
7×(-5) 4×(-5)
-8÷(-2) 4÷(-2)
改变
改变
7>4
...
...
...
结论:不等式两边乘(或除以)同一个负数,不等号的 方向改变.
<
>
教学目标
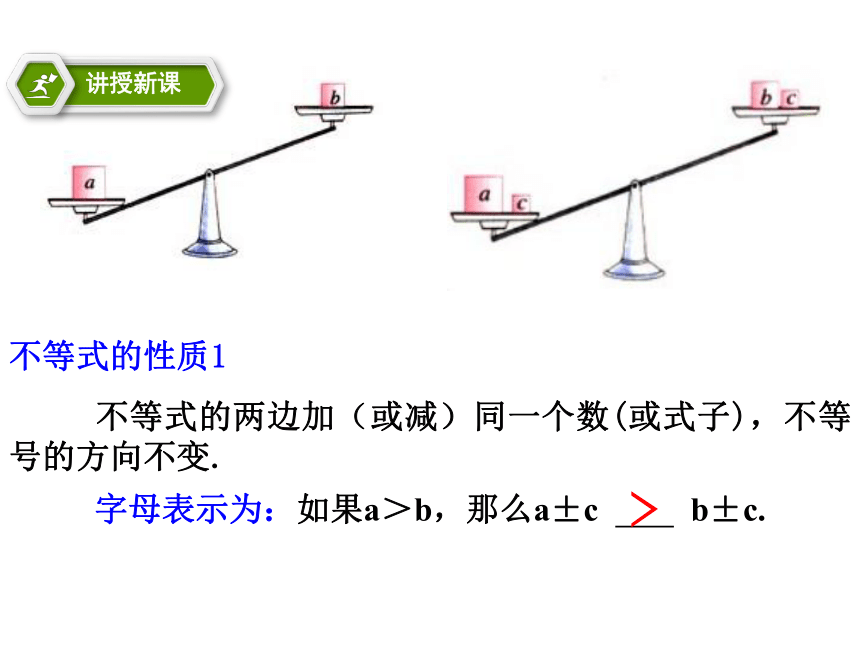
不等式的性质1
不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
字母表示为:如果a>b,那么a±c b±c.
﹥
教学目标
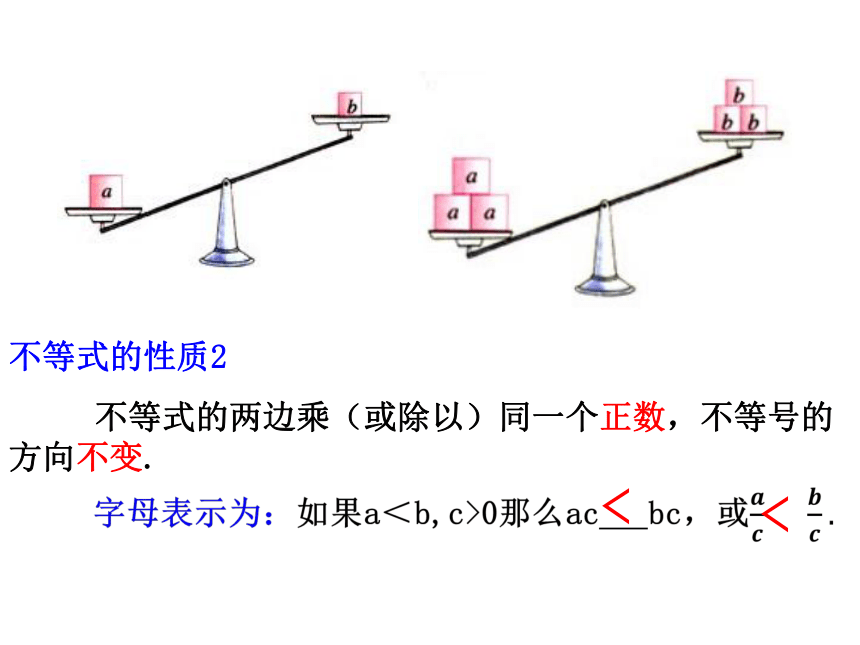
不等式的性质2
不等式的两边乘(或除以)同一个正数,不等号的方向不变.
﹤
﹤
不等式的性质3
不等式的两边乘(或除以)同一个负数,不等号的方向不变.
>
>
性质1:不等式两边加( 减去 )同一个正数,不等号的方 向不变.
性质2:不等式两边乘( 或除以 )同一个正数,不等号的 方向不变.
性质3:不等式两边乘( 或除以 )同一个负数,不等号的 方向改变.
不等式性质
四、成果展示,教师点拨
等式
不等式
基本性质1
基本性质2
基本性质3
若a<b,b<c,则a<c
如果a>b,那么
a+c>b+c,a-c>b-c
如果a=b,那么a+c=b+c,a-c=b-c
若a=b,b=c,则a=c
教学目标
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1、2、3
思路:
解:根据不等式的性质1,不等式两边都加7,不等号的 方向不变,得
x-7+7﹥26+7,
即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1) x-7>26
解:根据不等式的性质1,不等式两边都减去2x,不等
号的方向不变,得:
3x-2x﹤2x+1-2x
即x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
(2) 3x<2x+1;
这个不等式的解集在数轴上的表示如图所示:
0
75
即x>75
解:根据不等式的性质3,不等式两边都除以-4,不等号的方向改变,得
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
(4) -4x>3
例2:
解:不等式两边同时乘以12,得
2(5x+1)-2×12>3(x-5)
10x+2-24>3x-15
10x-3x>24-2-15
7x>7
X>1
去分母
拆括号
移项
合并同类项
系数化1
0
1
教学目标
教学目标
解不等式
1.利用不等式性质解不等式;
2.解的过程类似于:解一元一次方程;
3.在去分母和化系数为1时,注意不等号的方向.
4.在数轴上表示解集应注意的问题:方向、空心或实心.
问题:一辆轿车在一条规定车速不低于60km/h,且不高于100 km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢?
根据路程与速度、时间之间的关系可得:s≥60x,且s≤100x.
含“≤”“≥”的不等式
常用的表示不等关系的关键词语及对应的不等号:
关
键
词
语
第一类:明确表明数量
的不等关系
第二类:明确表明数量的范围特征
①大 于
②比…大
③超 过
①小 于
②比…小
③低 于
①不小于
②不低于
③至 少
①不大于
②不超过
③至 多
正
数
负
数
非
负
数
非
正
数
不
等
号
﹤
>
≥
≤
>0
﹤0
≥0
≤0
我们把用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.其中“≥”读作大于等于,“≤”读作小于等于.
不等式的概念
教学目标
例3:某长方体形状的容器长5cm,宽10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出V的取值范围.
解:新注入水体积V与原有水体积的和≤容器的容积,即
V+3×5×3≤3×5×10
解得V≤105
又由于新注入水的体积不能是负数,因此,V的取值范围是V≥0并且V≤105.
在数轴上表示V的取值范围如图:
在表示0和105的点上画实心圆点,表示取值范围包括这两个数.
0
105
利用不等式的性质解不等式的注意事项
2.要注意区分“大于” “不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来.
1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
不等式的传递性
教学目标
(1)10<20,20<60,则10 60.
(2)若a<b,b<c,则a c.
结论:若a<b, b<c, 则a<c.
不等式的传递性.
<
<
x>-1
不等式的基本性质2
不等式的基本性质3
1.填空:
五、知识验证提升
2:你能用不等式的基本性质判断下列说法的正误吗?
教学目标
(1)如果a>b,那么ac>bc.
(2)如果a>b,那么ac2>bc2.
(3)如果ac2>bc2,那么a>b.
×
×
√ 因为c≠0,所以c2>0.
当c≤0时,不成立.
当c=0时,不成立.
3.小希家距学校有2千米,而她的步行速度为每小时10千米.那么,小希若要8点之前到达学校,她上午几点从家里出发才能保证不迟到?
解:设小希上午x点从家里出发才,则:
答:小希上午7:48前时从家里出发才能不迟到.
教学目标
4.用不等式表示下列语句并写出解集,并在数轴上表示解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
教学目标
(2)x+3≥6, 解集是x≥3;
0
3
0
教学目标
5.如果关于x的不等式 (1-a)x>1-a 的解集为 x<1 ,那么请给出一个符合题意a的值.
解:由(1-a)x>1-a ,不等式两边同时除以 1-a ,得
x<1
∵不等号方向改变了,由不等式的性质3可知:
∴1-a<0,即a>1
∴可以取a=2
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
→
如果
那么
如果
那么
不等式的基本性质1
如果a>b,那么a+c>b+c,a-c>b-c
→
不等式的传递性:若a<b, b<c, 则a<c.
教学目标
课本119页练习第1题;
课本120页第4、5、7题.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的4倍小于或等于-2;
一、激发求知欲
2.等式的性质
猜想:不等式也具有同样的性质吗?
二、展示目标和任务
学习目标:
1、掌握不等式的三个基本性质。?
2、经历探究不等式基本性质的过程,体会不等式与等式的异同点。?
3、体会探索过程中所应用的归纳和类比方法。??
学习重点:
理解不等式的三个基本性质。??
学习难点:
对不等式的基本性质3的认识。
1.用 > 或 < 符号填空,并总结其中的规律:
(1) 5>3 , 5+2 3+2, 5-2 3-2
(2) -1<3, -1+2 3+2, -1-3 3-3
(3) 6>2, 6×5 2×5, 6×(-5) 2×(-5)
(4) -2<3, (-2)×6 3×6, (-2)×(-6) 3×(-6)
>
>
<
<
>
<
>
>
三、自主合作与交流
2.从以上练习中,你发现了什么规律?
(1)不等式的两边同时加(或减)同一个数,不等号的方向__________.
(2)不等式的两边同时乘(或除以)同一个正数,不等号的方向______________.
(3)不等式的两边同时乘(或除以)同一个负数,不等号的方向______________.
不变
不变
改变
教学目标
不等式
两边都加(或减去)同一个数
不等号方向
-8<4
7+5 4+5
-8-7 4-7
不变
不变
7>4
...
...
...
结论:不等式两边加(或减去)同一个数,
不等号的方向 不变.
>
<
教学目标
7×5 4×5
-8÷2 4÷2
结论:不等式两边乘或除以同一个正数,
不等号的方向不变.
>
<
教学目标
不等式
两边都加(或减去)同一个数
不等号方向
-8<4
不变
不变
7>4
...
...
...
不等式
两边都乘(或除以)同一正数
不等号方向
-8<4
7×(-5) 4×(-5)
-8÷(-2) 4÷(-2)
改变
改变
7>4
...
...
...
结论:不等式两边乘(或除以)同一个负数,不等号的 方向改变.
<
>
教学目标
不等式的性质1
不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
字母表示为:如果a>b,那么a±c b±c.
﹥
教学目标
不等式的性质2
不等式的两边乘(或除以)同一个正数,不等号的方向不变.
﹤
﹤
不等式的性质3
不等式的两边乘(或除以)同一个负数,不等号的方向不变.
>
>
性质1:不等式两边加( 减去 )同一个正数,不等号的方 向不变.
性质2:不等式两边乘( 或除以 )同一个正数,不等号的 方向不变.
性质3:不等式两边乘( 或除以 )同一个负数,不等号的 方向改变.
不等式性质
四、成果展示,教师点拨
等式
不等式
基本性质1
基本性质2
基本性质3
若a<b,b<c,则a<c
如果a>b,那么
a+c>b+c,a-c>b-c
如果a=b,那么a+c=b+c,a-c=b-c
若a=b,b=c,则a=c
教学目标
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1、2、3
思路:
解:根据不等式的性质1,不等式两边都加7,不等号的 方向不变,得
x-7+7﹥26+7,
即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
0
33
(1) x-7>26
解:根据不等式的性质1,不等式两边都减去2x,不等
号的方向不变,得:
3x-2x﹤2x+1-2x
即x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
(2) 3x<2x+1;
这个不等式的解集在数轴上的表示如图所示:
0
75
即x>75
解:根据不等式的性质3,不等式两边都除以-4,不等号的方向改变,得
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
(4) -4x>3
例2:
解:不等式两边同时乘以12,得
2(5x+1)-2×12>3(x-5)
10x+2-24>3x-15
10x-3x>24-2-15
7x>7
X>1
去分母
拆括号
移项
合并同类项
系数化1
0
1
教学目标
教学目标
解不等式
1.利用不等式性质解不等式;
2.解的过程类似于:解一元一次方程;
3.在去分母和化系数为1时,注意不等号的方向.
4.在数轴上表示解集应注意的问题:方向、空心或实心.
问题:一辆轿车在一条规定车速不低于60km/h,且不高于100 km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢?
根据路程与速度、时间之间的关系可得:s≥60x,且s≤100x.
含“≤”“≥”的不等式
常用的表示不等关系的关键词语及对应的不等号:
关
键
词
语
第一类:明确表明数量
的不等关系
第二类:明确表明数量的范围特征
①大 于
②比…大
③超 过
①小 于
②比…小
③低 于
①不小于
②不低于
③至 少
①不大于
②不超过
③至 多
正
数
负
数
非
负
数
非
正
数
不
等
号
﹤
>
≥
≤
>0
﹤0
≥0
≤0
我们把用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.其中“≥”读作大于等于,“≤”读作小于等于.
不等式的概念
教学目标
例3:某长方体形状的容器长5cm,宽10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出V的取值范围.
解:新注入水体积V与原有水体积的和≤容器的容积,即
V+3×5×3≤3×5×10
解得V≤105
又由于新注入水的体积不能是负数,因此,V的取值范围是V≥0并且V≤105.
在数轴上表示V的取值范围如图:
在表示0和105的点上画实心圆点,表示取值范围包括这两个数.
0
105
利用不等式的性质解不等式的注意事项
2.要注意区分“大于” “不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来.
1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
不等式的传递性
教学目标
(1)10<20,20<60,则10 60.
(2)若a<b,b<c,则a c.
结论:若a<b, b<c, 则a<c.
不等式的传递性.
<
<
x>-1
不等式的基本性质2
不等式的基本性质3
1.填空:
五、知识验证提升
2:你能用不等式的基本性质判断下列说法的正误吗?
教学目标
(1)如果a>b,那么ac>bc.
(2)如果a>b,那么ac2>bc2.
(3)如果ac2>bc2,那么a>b.
×
×
√ 因为c≠0,所以c2>0.
当c≤0时,不成立.
当c=0时,不成立.
3.小希家距学校有2千米,而她的步行速度为每小时10千米.那么,小希若要8点之前到达学校,她上午几点从家里出发才能保证不迟到?
解:设小希上午x点从家里出发才,则:
答:小希上午7:48前时从家里出发才能不迟到.
教学目标
4.用不等式表示下列语句并写出解集,并在数轴上表示解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
教学目标
(2)x+3≥6, 解集是x≥3;
0
3
0
教学目标
5.如果关于x的不等式 (1-a)x>1-a 的解集为 x<1 ,那么请给出一个符合题意a的值.
解:由(1-a)x>1-a ,不等式两边同时除以 1-a ,得
x<1
∵不等号方向改变了,由不等式的性质3可知:
∴1-a<0,即a>1
∴可以取a=2
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
→
如果
那么
如果
那么
不等式的基本性质1
如果a>b,那么a+c>b+c,a-c>b-c
→
不等式的传递性:若a<b, b<c, 则a<c.
教学目标
课本119页练习第1题;
课本120页第4、5、7题.
